Rep:Llt15 TS

Transition States and Reactivity

Introduction

A transition state is the saddle point which is a local maxima on the minimum energy path linking reactants and the products whereas the reactants and products correspond to the minimum in the potential energy surface (PES). Therefore, at both minimum point and transition structure, the total gradient of the potential energy surface will have a value of zero. This is defined by the first derivative of potential energy vs bond distances graph: ∂V(r_i)/∂r_i = 0

For non-linear molecules, there are 3N - 6 normal vibrational modes or so-called degree of freedom. Using a harmonic oscillator model, each vibrational modes has the restoring force defined by Hookes law:

F = -kx 
where 'k' is the force/spring constant
      'x' is the displacement of spring which resemble bonds from its equilibrium position.

The reactants and products sit in a well at the minimum and vibrate 'forever' unless sufficient energy is provided for them to react. The transition state has a different mode of vibration along the reaction coordinate which take the TS downhill towards the reactant or product, without a restoring force. This lead to a negative k. Thus, the calculation of second derivative of the curvature (k) in the PES (∂²V(r_i)/∂r_i²) helps to distinguish the minimum and TS. As the frequency calculation involves taking square root of a force constant k and the square root of negative value leads to an imaginary number, at every transition state there must be only one imaginary frequency as all other coordinates are minimised. Hence, it is concluded that a negative value of second derivative of gradient indicated a transition structure whereas positive value represented the minimum point (reactant and product) of the reaction path and the same thing applies in frequency calculation.

Figure 1. Equation to calculate the vibrational frequency (\nu) for diatomic molecules

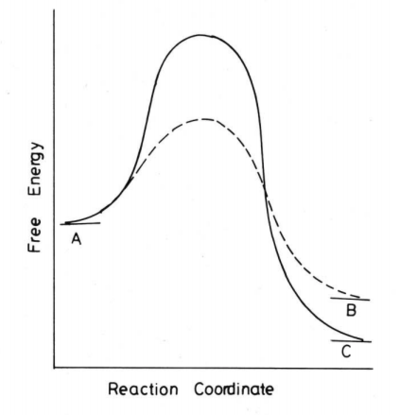
For a thermodynamically controlled reaction, the reaction is reversible and the energetically more stable product is favoured. Therefore, the relative energy of transition state is not important as the product with the lowest energy (most stabilized) will eventually predominate under equilibrating condition. For a kinetic controlled reaction, the energy of the transition state determines the predominant product as the product forms irreversibly once the TS is reached. Hence, the pathway that requires lower activation energy to reach the transition state will be chosen. As a result, the most rapidly formed product predominates under kinetic control reaction.

Figure 2. Schematic diagram for kinetic versus thermodynamic control

Nf710 (talk) 23:22, 7 November 2017 (UTC) Good understanding of a TS. You could have shown more undertsanding saying the are 3N-6 degrees of freedom. each one of them correspondong to a normal mode and has its own force constant and hence vibration.

23:25, 7 November 2017 (UTC) You could have also talked about some of the quantum mechanical methods

Exercise 1: Cycloaddition of Butadiene and Ethylene

Figure 3. Reaction scheme for cycloaddition of 1,3-butadiene and ethylene.

Method used for optimization and analysis:

The geometry of the reactants are optimized at PM6 level and the optimized reactants are used to construct the transition state of the reaction. The distance 2.20 Å is used in the guess of TS for the approximate separation between the terminal carbon atoms in both reactants as this is the intermediate value between a normal C-C single bond and the Van der Waals distance of 2 carbon atoms. The guess TS structure is optimized at PM6 level and the optimized TS is used to run a IRC to obtained the product. The product is again optimized to a minimum at PM6 level. The optimized structure of reactants, transition state and product are shown in table 1.

Table 1. Optimized structures by PM6 calculation

Optimized Structure
1,3-butadiene	Ethylene	Transition State	Cyclohexene

Correlate these MOs with the ones in your MO diagram to show which orbitals interact. What can you conclude about the requirements for symmetry for a reaction (when is a reaction 'allowed' and when is it 'forbidden')?

Table 2. HOMO and LUMO of reactants and transition state (TS)

Chemical Structure	HOMO	LUMO	MO interactions
Butadiene	MO11 (Aysmmetric)	MO12 (Symmetric)	Figure 4. Idealized MO diagram of [4+2] cycloaddition with with labelled symmetry (Antisymmetric= A, Symmetric= S).
Ethylene	MO6 (Symmetric)	MO7 (Asymmetric)
Transition State	MO16 (HOMO -1) MO17 (HOMO)	MO19 (LUMO + 1) MO18 (LUMO)

The HOMO-LUMO interactions shown in the MO diagram of the cycloaddition between butadiene and ethylene are listed below:

 Butadiene HOMO (MO 11, A) + Ethylene LUMO (MO 7, A) = Transition State HOMO (MO 16)
 Butadiene HOMO (MO 11, A) - Ethylene LUMO (MO 7, A) = Transition State LUMO (MO 19)

 Butadiene LUMO (MO 12, S) + Ethylene HOMO (MO 6, S) = Transition State HOMO (MO 17)
 Butadiene LUMO (MO 12, S) - Ethylene HOMO (MO 6, S) = Transition State LUMO (MO 18)

The symmetry label 'A' and 'S' corresponds to whether the molecular orbital (MO) is asymmetrical or symmetrical with respect to the mirror plane orthogonal to the sigma bond which lies in the middle of MO.

(Fv611 (talk) 16:59, 1 November 2017 (UTC) Your MO diagram and calculated MOs are very good, however you could have pushed the symmetry discussion. You don't underline that MOs with the same symmetry combine with each other to give a TS MO with the same symmetry. The symmetries have to be matching because (as you mention later) a combination of A and S orbitals gives a zero overlap integral.)

According to the Woodward Hoffmann rules, the total number of (4q + 2)_s + (4r)_a must be odd for the pericyclic reaction to be thermally allowed. The letters 'q' and 'r' stand for integer starting from zero whereas the suffix 's' stands for suprafacial and 'a' for antarafacial. A suprafacial component forms new bonds on the same face whereas an antarafacial components formes new bonds on opposite faces at both ends. However, the reaction is considered to be thermally forbidden but photochemically allowed if the total number of (4q + 2)_s + (4r)_a equals to zero or an even number.

The [_π4_s + _π2_s] cycloaddition between butadiene and ethylene is allowed as shown:

   (4q + 2)s + (4r)a
   = 1 + 0
   = 1
   = thermally allowed reaction when q and r equal to 0

Write whether the orbital overlap integral is zero or non-zero for the case of a symmetric-antisymmetric interaction, a symmetric-symmetric interaction and an antisymmetric-antisymmetric interaction:

Table 3. Effect of the symmetry of interactions on the orbital overlap integral

Type of interactions	Orbital overlap integral
Symmetric-symmetric	Non-zero
Symmetric-antisymmetric	Zero
Antisymmetric-antisymmetric	Non-zero

Include measurements of the 4 C-C bond lengths of the reactants and the 6 C-C bond lengths of the TS and products. How do the bond lengths change as the reaction progresses?

Table 4. The changes in bond length of the reactants, TS and product molecules as reaction progress

Molecules	C-C Bond lenghths	Molecules	C-C Bond lenghths
Reactant: Ethylene	C1-C4 (double bond)= 1.33 Å	Reactant: 1,3-Butadiene	C1-C4 (double bond)= 1.34 Å C4-C6 (single bond) = 1.47 Å C6-C7 (double bond)= 1.34 Å
Transition State	C1-C4 (double bond-breaking)= 1.38 Å C4-C6 (double bond-forming) = 1.41 Å C6-C7 (double bond-breaking)= 1.38 Å C7-C11 (single bond-forming) = 2.11 Å C11-C14 (double bond-breaking)= 1.38 Å C14-C1 (single bond-forming) = 2.11 Å	Product: Cyclohexene	C6-C4 = 1.34 Å, C=C sp2-sp2 bond C4-C1 = 1.50 Å, C-C sp3-sp2 bond C1-C14 = 1.54 Å, C-C sp3-sp3 bond C14-C11 = 1.54 Å, C-C sp3-sp3 bond C11-C7 = 1.54 Å, C-C sp3-sp3 bond C7-C6 = 1.50 Å, C-C sp3-sp2 bond

What are typical sp3 and sp2 C-C bond lengths? What is the Van der Waals radius of the C atom? How does this compare with the length of the partly formed C-C bonds in the TS.

Typical C-C bond length:

sp³-sp³: 1.54 Å

sp³-sp²: 1.50 Å

sp²-sp²: 1.47 Å

Van der Waals radius of a carbon atom: 1.70 Å
Van der Waals distance of 2 carbon atoms: 3.40 Å

In the transition state of cycloaddition process between butadiene and ethylene, the partly formed C-C single bond lengths are about 2.12 Å which is an intermediate value between typical sp³ C-C bond length and Van der Waals distance of 2 carbon atoms. For the breaking double bond, the bond lengths are increased upon the change in the carbon hybridisation from sp² to sp³. In other words, the reduced in s orbital character from sp²(33%) to sp³(25%) makes the C-C bond longer and weaker as the electrons are less strongly held to the nucleus. On the other hand, the single bond on butadiene is shorter in the transition state as the carbon is hybridised from sp³ to sp² upon double bond formation.

For cyclohexene, there is only a double bond between the sp² hybridised C6 and C7, and the remaining carbons are sp³ hybridised. Thus, there is no delocalisation of electron cloud in the cyclohexene and the electrons are localised along the C-C bond. This explains the existence of the three different bond lengths (1.34 Å, 1.50 Å and 1.54 Å) as the C-C bond lengths vary based on different carbon hybridisation.

Table 5. The changes in bond length along the reaction path

Type of Bond	Bond Length vs reaction coordinate	Discussion
C1-C4 and C6-C7 and C11-C14		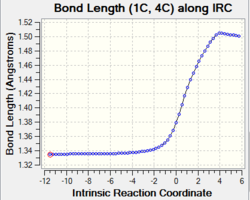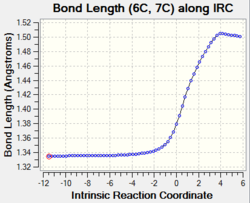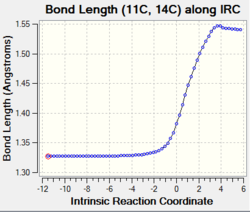Change in bond order: double bond to single bond The graphs show that the bond length increase gradually from 1.34 Å to 1.50 Å upon product formation. The increase in bond length indicates the breaking of the C1-C4 and C6-C7 double bonds due to the change in carbon hybridisation (C1, C7, C11 and C14) from sp2 to sp3. This causes a decrease in electron density between two carbons thus the single bonds are weaken and lengthen.
C4-C6		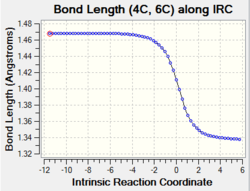Change in bond order: single bond to double bond The graph shows that the bond length decreases gradually from 1.47 Å to 1.34 Å upon product formation. The decrease in bond length indicates the double bond formation between C4 and C6. The additional pi overlap between C4-C6 strengthen the bond and hold the 2 carbon nucleus stronger together resulting in a shorter bond length.
C7-C11 and C14-C1		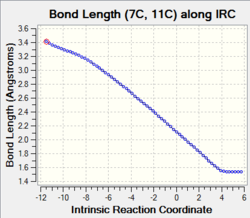The graphs show a steep decrease in bond length (or distance between 2 carbons) along the reaction coordinate. In this case, the two non-bonding carbon atoms from 1,3-butadiene and ethylene approach each other from Van der Waals distance (3.40 Å) and their orbitals start to overlap across the space in the transition state in order to form the new single bonds in the product stage. All of the 4 carbons change their hybridisation (sp2 to sp3) to form 2 new sigma bonds with typical carbon sp3-sp3 bond length at 1.54 Å.

Illustrate the vibration that corresponds to the reaction path at the transition state (TS). Is the formation of the two bonds synchronous or asynchronous?

Figure 5. Imaginary vibration of the TS of 1,3-butadiene and ethylene

The vibration mode that resembles to the reaction coordinate at TS is shown in figure 4.
This mode has a negative force constant which results in an imaginary frequency of value -949 cm^-1.
From the animation, it shows that the concerted formation of the two new C-C bonds is synchronous in terms of the movement of the 2 terminal carbons of 1,3-butadiene and the 2 carbons of ethylene towards each other at the same rate to form the product cyclohexene.

Additional information

For exercise 2, go to https://wiki.ch.ic.ac.uk/wiki/index.php?title=Llt15_TS_2
For exercise 3, go to https://wiki.ch.ic.ac.uk/wiki/index.php?title=Llt15_TS_3

log file for IRC calculation is for exercise 1 available at File:TRIAL TS 2 IRC CORRECTED LLT15.LOG