Rep:LH3115TSS
Transition State Structures
Introduction
Gaussian basis functions have been used to calculate wavefunctions for a long time, like Hartree-Fock functions. The Hartree-Fock method uses a series of approximations to solve the time ondependent Schrödinger Equation and because Molecular Orbitals are linear combinations of atomic orbitals, this involves solving matrices. However due to the time-consuming nature of these calculations, reducing the number of iterations becomes necessary for big systems[1]. In this experiment two methods have been used to calculate the Molecular Orbitals of 3 different reactions. The first used is a semi empirical method called PM6 (Parameterization Method 6), is a relatively quick method that doesn’t calculate all the values of the matrices to evaluate the MO, instead it uses empirical values [2]. The other one is under DFT (Density Functional Theory) methods called B3LYP method, which is a hybrid function that uses both Hatree-Fock and DFT methods. The 6-31G basis set was used for all B3LYP calculations in this experiment [3].
Nf710 (talk) 22:03, 7 March 2018 (UTC) You have shown a good understanding here, you have clear read beyond the script but you could have used some equations to back up your arguement.
In this experiment 3 reactions were investigated, each with its different Transition State to result in different products. In a 3 dimensional molecule there are 3N-6 (N = number of atoms in molecule)degrees of freedom for vibrations. The TS is located by calculating the second derivative at a particular vibration. The TS will be at the saddle point, which will have one negative second derivative frequency as a saddle point has a first derivative equal to 0 in one direction (vibrations in this case) and a negative second in the same direction, all other directions would increase the energy of the reaction at that point. All minimum points (Reactants and Products)have no negative frequencys as the second derivative at a minimum is positive in all directions.
Nf710 (talk) 22:03, 7 March 2018 (UTC) Not sure what you eman by 3 dimensionsal molecule. Your discussion is correct, but you should talk about diagonalising the hessian matrix. the eigenvalues give you the second derivatives.
Exercise 1
(Fv611 (talk) Good, concise section. Well done :) )
Diels-Alder reaction
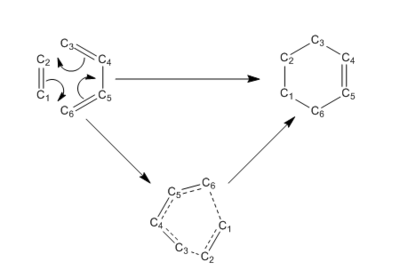
The Reactant, Product and Transition State structures of the [4+2] cycloaddition shown in figure 1 were calculated using the PM6 method. According to the calulations the Ethene approaches the Butadiene from below or above resulting in a stacked TS.
Molecular Orbitals

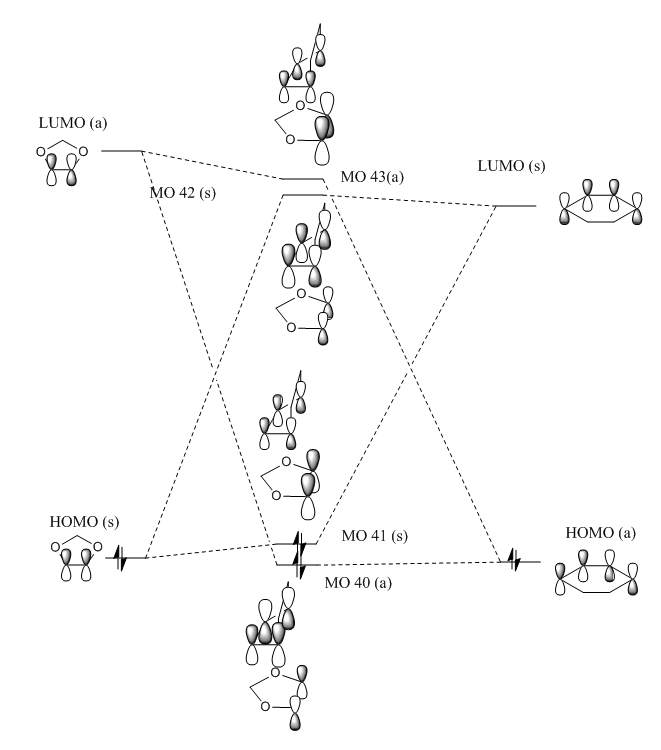
In the MO diagram in figure 2 one can see the relative different Energie-levels which correspond to the energies calculated from Gaussview 5.0. In the MO diagram one can see that only orbitals interact that have the same symmetry, so it can be concluded that a reaction is only allowed if orbitals of the same symmetry can interact. The orbitals overlap is zero for all antisymmetric-symmetric interactions and non-zero for all interaction of antisymmetric-antisymmetric and symmetric-symmetric interactions. Note that reactant orbitals that are closer in energy to the TS state orbitals contribute more to the bonding which is illustrated in the MO diagram.
J mol files
The following link is to the Jmols of the Reactant MOs and Transition state MOs seen in figure 2.
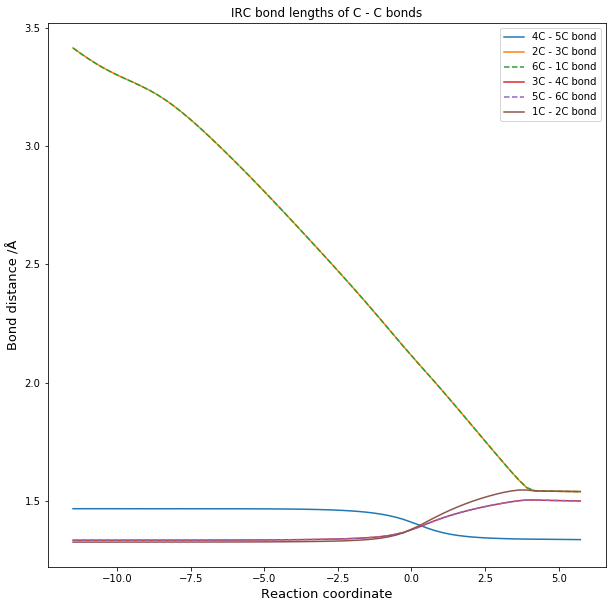
C - C bond lengths
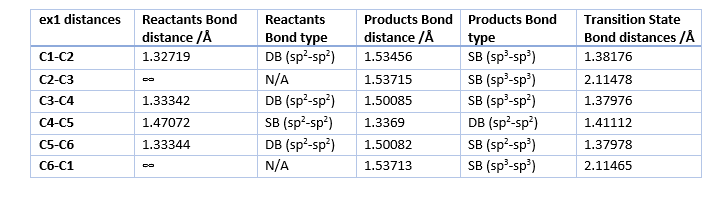
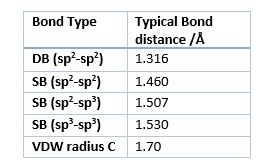
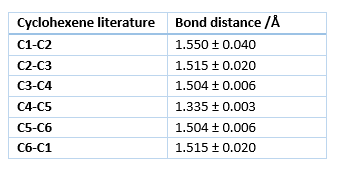
The distances in table 1 correspond to the results obtained from the optimizations using the PM6 method while table 2 gives the typical bond lengths found in literature.
During the reaction the 3 C-C double bonds break to form 2 new single bonds, connecting the Ethene and the Butadiene and creates a new double bond. Due to the change in bonding and hybridization of the C atoms all of the bond lengths change. All of the single bonds of the products are within 0.01 Å of the typical single bond lengths for all the different hybridizations present, while the double bond in the product is off by 0.015 Å. However the literature values for the bond lengths in cyclohexene show that the calculated values are almost identical with data from literature seen in table 3.[5]This suggests that the difference in bond lengths from the typical values is due to the structural strain of the ring and and not due to the accuracy of the method used. Given the accuracy of the values obtained from the PM6 method, any further optimization with the B3LYP method is not necessary.
For the reactants the bond lengths are within 0.015 Å of the typical values in table 2. In this case the differences seem to be due to the method used and a optimization with the B3LYP would most likely result in more accurate bond lengths. However the obtained values are still very close to the typical values.
The Bond lengths of the Transition state reflect the stage at which the reaction is very well as the newly formed single bond of C2-C3 and C6-C1 are the longest as they being newly formed. These are the only once that have a bond length larger than that of the Van der Walls radius of carbon seen in table 2. However the length is less than twice the VDW radius of C, which means that there is a orbital interaction between the atoms.
All other Transition bonds have distance more similar to the reactant distances with fits with Hammond's postulate , which states that the Transition State is closest in structure to the structure that it is closest in energy to. As this reaction is endothermic, the reactants total energie are closer in energy to the transition state.
Figure 3 visualizes how bond lengths are changing in the course of the reaction compared to each other.
Reaction
Gif 2 shows that the formation of the two bonds is synchronous as both bonds form in the same moment. This corresponds to theory as literature says that the Diels-Alder reaction proceeds via a concerted mechanism, which makes our simulation accurate.
Files
File:Product ex1 LH3115.LOG File:EX1 IRC LH3115.LOG
Exercise 2
Reaction Scheme

The reaction of 1,3-Dioxol and Cyclohexadiene gives two stereoisomers due to the dieneophiles substituent, an Endo and an Exo product. The Endo product is formed when the substituent of the dienophile is oriented towards the diene, while in the Exo product in orients away from the diene. This is illustrated in figure 4 in the Transition States, note that in this case it doesn't matter whether the dieneophile approaches from the top or from the bottom.
MO Diagrams
(Fv611 (talk) Your MO diagrams are good, but you could have extended the discussion to cover the differences between endo and exo conformations in terms of the relative energies of their MOs.)
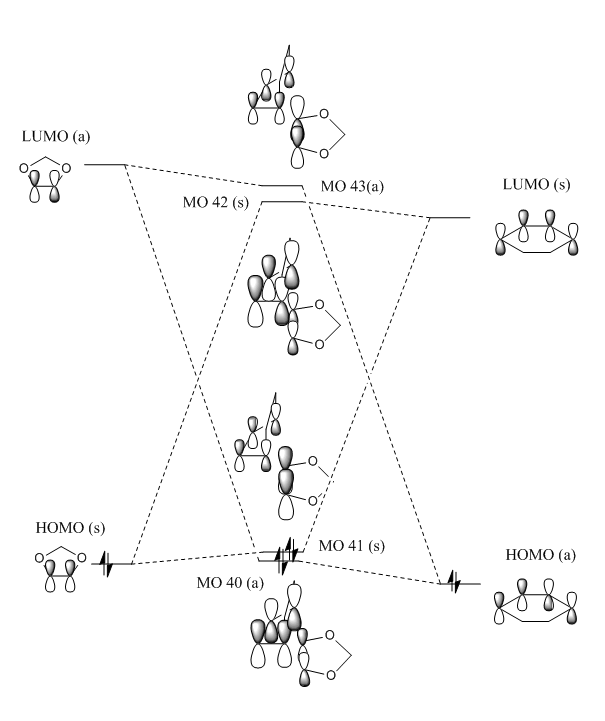
Figures 5 and 6 below show the MO diagram of the TS state energies of the Endo and Exo Products. The Jmol files for the optimized Reactants, Products and Transition States are here. All the structures were initially calculated using the PM6 method and then were further optimized using B3LYP.
Both MO diagrams were drawn with the relative size of the contributing orbitals in mind, like in exercise 1, therefore some orbitals are bigger depending on how close in Energy the relevant reactant MO is to the Transition State MO.
The Diels-Alder reaction has an inverse electron demand as the HOMO of the Dienophile and the LUMO of the Diene are closer in energy than the LUMO of the Dienophile and the HOMO of the Diene. This is because the 1,3-Dioxole is particularly electron rich, due to the electron donating oxygen, which increases the energy of it's HOMO and LUMO. However the LUMOdienophile and HOMOdiene in this reaction result in a lower energy bonding orbital for the Transition State, which is unusual as the closer energy levels are the greater the energy splitting usually. This suggests that the orbital overlap is smaller, or other orbitals contribute to the overall bonding of this orbital.
Nf710 (talk) 22:12, 7 March 2018 (UTC) How do you know this? You have just stated this and not given any evidence. You should have given the data from the single point energy.
 |
 |
Kinetic and Thermodynamic product
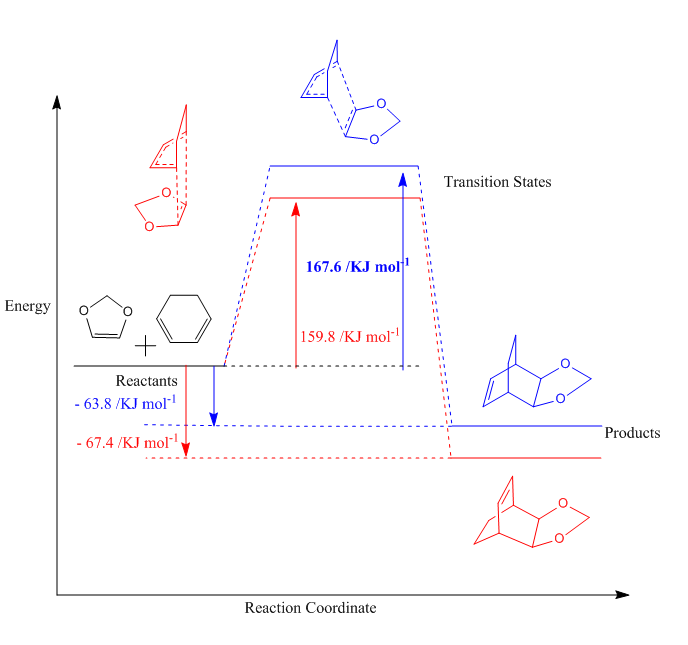

The energies of the reaction are shown in table 4, with the activation and reaction energies visualized in a reaction profile in figure 7. In the reaction profile the Endo product is both kinetically and thermodynamically more favorable as the TS energy and Product energy is lower than those of the Exo reaction. That means that it is kinetic product has it can traverse the TS faster, as it is lower energie and it is the thermodynamic product as it is at lower energy.
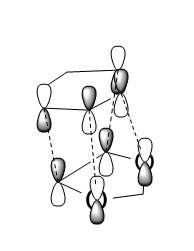
The reason for the stability of the Endo product is the orbital interaction illustrated in figure 8, where the orbitals on the Oxygen atoms interact with the pi system of the diene ring resulting in increased stability of the Transition State. A similar interaction is also present in the product where the \pi orbitals interact with the orbitals on the Oxygen atoms, however due to a greater distance between these two there is less orbital overlab thus the difference in reaction energies is less than the difference in activation energies. This is called the Endo rule and due to the similarity of the 2 structures this is most likely the major effect on the energies of the system. Steric effects seem to have little impact as the angle between the dioxol and the ring in the Exo product (113.895 o) is very similar to the angle of the dioxol and the ring in the Endo structure (113.751 o).
Nf710 (talk) 22:16, 7 March 2018 (UTC) Your energies are correct and you have come to the correct conclusion. however sterics do have an effect if you look at the bridge head hydrogens on the exo. you could have also gone into more deatils about the kinetics of the reaction and the electron demand.
Files
File:EX2 EXO IRC LH3115.LOG File:EX2 ENDO IRC LH3115.LOG
Exercise 3
Reaction Scheme
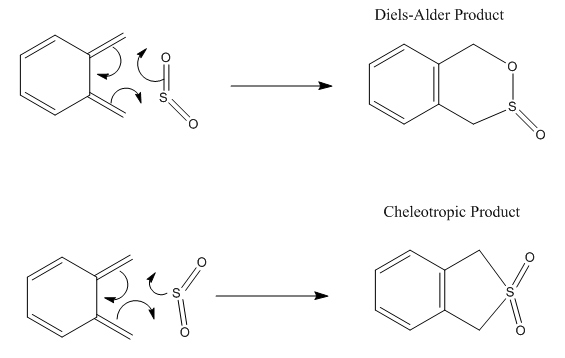
The reaction of the external diene of o-xylylene with SO2 is shown in figure 9, with both mechanisms. All of the possible reactions were calculated by IRC with the PM6 method and are shown in the Gifs 3 to 5.
As seen in the reaction scheme and the GIF files, in the Diels Alder reaction only the orientation of the molecules is important but not whether they approach from the top or the bottom. In the Cheletropic mechanism it is the same. Note that the SO2 approaches at an angle not from the side, in order to maximize orbital overlap with the π* of the diene.
Energies of the Reactions
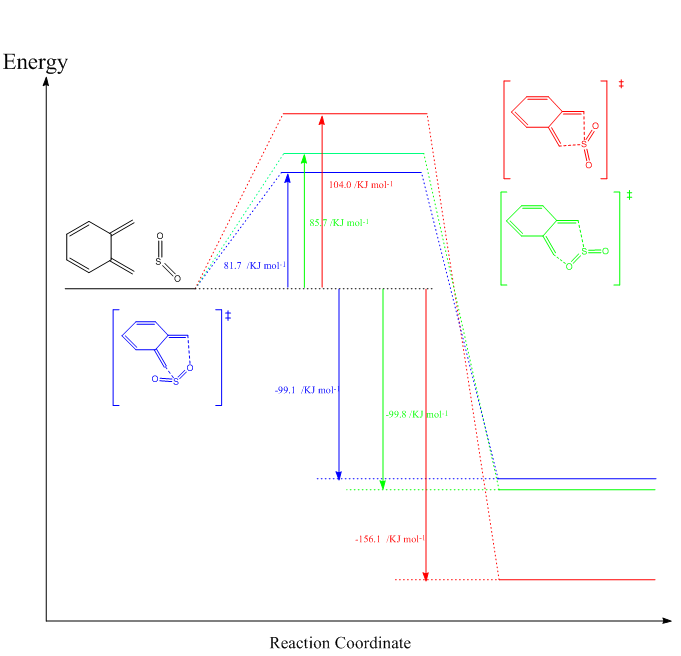
(It's quite hard to read bright green on white! Tam10 (talk) 15:13, 6 March 2018 (UTC))

The energies of the reactants and products are shown in Table 5, with the reaction profile being in figure 9. In the plot one can see that the thermodynamically preferred pathways are inverse to the kinetic ones. As the thermodynamic product is the cheletropic one, however it has the highest energy TS, while the Endo product of the Diels-Alder reaction is the kinetic product as it has the lowest TS energy but conversely has the highest final energy.
The difference in TS energies of the two Diels Alder pathways is likely due to the before mentioned (Exercise 2) orbital overlap of the oxygen substituent with the diene π orbitals. The cheletropic pathway has no π orbitals interacting instead uses the orbitals on sulfur to the reaction which leads to a higher energy TS.
The products itself are all favorable, because of the formation of the aromatic ring which is a lot more stable than normal conjugated systems.
The cheletropic product is most likely more stable for steric reasons as the sulfur atom is much larger than a C atom, which makes a five membered ring with sulfur more stable than a six membered ring with oxygen and sulfur resulting in more strain. In the IRC files in Gifs 1 to 3 it can be seen that the final products of the Diels Alder reactions are non planar with sulfur sticking out, while the cheletropic product is planar. Orbitals have an impact on the energy too as the cheletropic product uses different orbitals to bond to the C atoms than the Diels Alder ones.
The very small difference in energy of the two DA products is most likely a result of steric strain of the oxygen with the aromatic ring in the Endo product.
Internal Ring Reaction
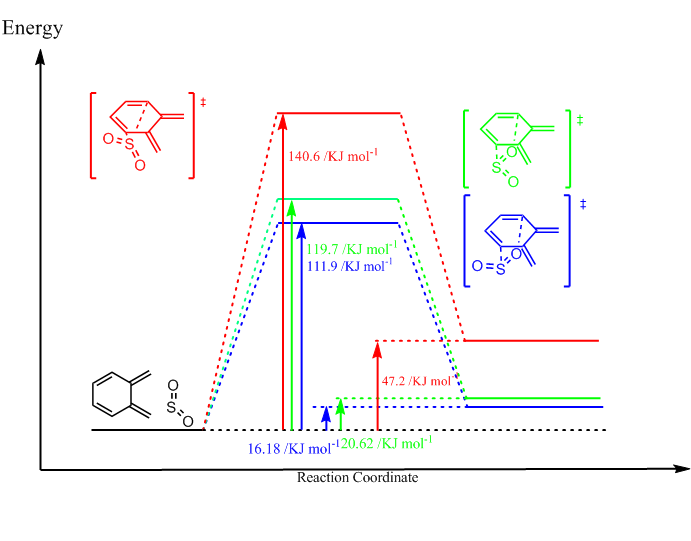

The reaction can theoretically also proceed with the diene within the ring of o-xylylene, however as shown in figure 10, all products of this reaction would be higher in energy than the reactants. This is because there would be no aromatic ring formation like in the reaction with the external diene. There would also be additional steric strain within the products, seen in the GIF files 6 to 8.
The reaction profile shows the big effect sterics have on this system as cheletropic product has by far the highest energy, most likely because it forms a five membered ring to the strained system while the DA products from a more open cage structure.
So in this case it would be more favorable to stay reactants at infinite seperation.
Note that the Endo product is both the thermodynamic and the Kinetic product in this reaction.
Files
File:EX3 XYLYLENE LH3115.LOG File:EX3 SO2 LH3115.LOG File:EX3 EXO PRODUCT LH3115.LOG File:EX3 EXO TS LH3115.LOG File:EX3 EXO IRC LH3115.LOG File:EX3 ENDO LH3115.LOG File:EX3 ENDO IRC LH3115.LOG File:EX3 ENDO TS LH3115.LOG File:EX3 CHELE Product LH3115.LOG File:EX3 CHELE IRC LH3115.LOG File:EXOINT TS LH3115.LOG File:EXOINT Product LH3115.LOG File:EXOINT IRC LH3115.LOG File:ENDOINT TS LH3115.LOG File:ENDOINT Product LH3115.LOG File:ENDOINT IRC LH3115.LOG File:CHELEINT IRC LH3115.LOG File:CHELEINT TS LH3115.LOG File:CHELEINT Product LH3115.LOG
Conclusion
The calculations run in this lab confirm the mechanisms of the Diels-Alder reaction and their predicted Transition States.
Gaussian optimizations prove a useful way analyzing molecules and predicting outcomes of reactions. It seems very useful in identifying which molecules are more the Thermodynamic and Kinetic products, enabling chemists to adapt their reaction conditions to obtain the highest yield possible. It is also a useful first step in determining whether or not a structure is energetically feasible or favorable and giving answers to why some structures are not forming. It also shows potential side products and different reaction paths, confirms mechanisms and product structures. The MO orbitals calculated and visualized give a much better understanding in the bonding involved and how the molecule is stabilized as the calculations take into account multiple neighbour interactions.
The lab also shows the different inaccuracies of the different calculation types.
However in order for the optimizations to work, knowledge of the mechanism and the Transition State is required, especially for systems with many degrees of freedom. Given the computational costs of some calculations it is not the best way to determine the TS of a reaction.
references
- ↑ T. H. Dunning Jr, J. Chem. Phys., 1970, 53, 2823-2833.
- ↑ Gaussian: Semi-Empirical Methods: http://gaussian.com/semiempirical/
- ↑ Gaussian: Density Functional (DFT) Methods: http://gaussian.com/dft/
- ↑ Handbook of Chemistry & Physics (65th ed.). CRC Press. ISBN 0-8493-0465-2..
- ↑ 5.0 5.1 J. F. Chiang and S. H. Bauer, J. Am. Chem. Soc., 1969, 91, 1898-1901.