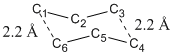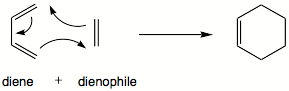Rep:Km1710

Module 3: Investigating Transition States in Organic Reactions

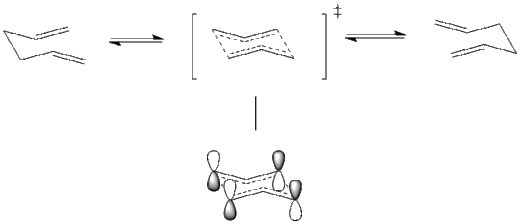
Pericyclic reactions have been widely studied and developed in many organic synthesis routes, as well as biochemistry processes. They are usually characterized as concerted reactions with cyclic transition states. It usually involves large molecules with varied structures, therefore, investigation into the quantitative characters becomes important in determining the exact mechanisms.

In this experiment, two typical pericyclic reactions, namely the cope rearrangement and the Diels Alder cycloaddition, are investigated by molecular orbital based methods. The molecular mechanics methods which have been used previously for structure determining do not work for this case because it does not involve bond making or breaking processes as well as change of electron distribution, which is important in studies in transition states. By quantifying the total energy of transition state, more detailed studies into the reaction mechanisms can be determined. Furthermore, modified mechanisms for different pericyclic reactions will be compared and discussed.

Example a: The Cope Rearrangement

The Cope rearrangement involves a [3,3]-sigmatropic shift rearrangement of 1,5-hexadiene. The mechanism is usually recognized as a concerted process via either a 'chair' or a 'boat' transition structure. The preferred configuration of both reactant and product, as well as the transition state, will be modified in order to give the precise reaction mechanism.

A general reaction mechanism for the Cope rearrangement is drawn as following:

Optimization of the Reactant and Product

In the first stage, a less accurate HF/3-21G method is used in order to make comparison between the relative total energies of different structures. After finding the structure which lies in the lowest energy state, further optimization with more accurate methods will be made.

Optimization of Anti-Peri Planar Conformer of 1,5-hexadiene

1. Optimized Anti Structure

test molecule

2. Key Information of Result

Type of Conformer	Anti 1
Method	Optimization to a minimum
Basis Set	HF/3-21G
Memory Limit	250 MB
Total Energy	-231.69260233 a.u.
Current Symmetry Group	C2

3. Validity of Result

3.1 Real Output

        Item               Value     Threshold  Converged?
Maximum Force            0.000025     0.000450     YES
RMS     Force            0.000009     0.000300     YES
Maximum Displacement     0.001256     0.001800     YES
RMS     Displacement     0.000428     0.001200     YES
Predicted change in Energy=-5.174799D-08
Optimization completed.
   -- Stationary point found.

Both force and displacement converged. This confirms the optimization is successful and the resultant molecule is in its energy minimum.

3.2 Frequency Analysis

Frequency analysis carried out from the previously optimized file shows all the frequencies have positive values (from 76.47 cm^-1 to 3385.85 cm^-1), therefore double confirms the optimization is correct.

4. File Link

To access the .log file of optimization, click here; for the .log file of frequency analysis, click here.

To view the screenshot of the calculation summary table, click here.

To view the screenshot of the symmetry table, click here.

Optimization of Gauche Conformer of 1,5-hexadiene

1. Optimized Gauche Structure

test molecule

2. Key Information of Result

Type of Conformer	Gauche 4
Method	Optimization to a minimum
Basis Set	HF/3-21G
Memory Limit	250 MB
Total Energy	-231.69153032 a.u.
Current Symmetry Group	C2

3. Validity of Result

3.1 Real Output

        Item               Value     Threshold  Converged?
Maximum Force            0.000018     0.000450     YES
RMS     Force            0.000008     0.000300     YES
Maximum Displacement     0.001627     0.001800     YES
RMS     Displacement     0.000413     0.001200     YES
Predicted change in Energy=-4.921086D-08
Optimization completed.
   -- Stationary point found.

Both force and displacement converged. This confirms the optimization is successful and the resultant molecule is in its energy minimum.

3.2 Frequency Analysis

Frequency analysis carried out from the previously optimized file shows all the frequencies have positive values (from 65.47 cm^-1 to 3385.37 cm^-1), therefore double confirms the optimization is correct.

4. File Link

To access the .log file of optimization, click here; for the .log file of frequency analysis, click here.

To view the screenshot of the calculation summary table, click here; click here for symmetry information.

Optimization of Anti-Peri Planar Conformer of 1,5-hexadiene (anti 2)

1. Optimized Anti 2 Structure

test molecule

2. Key Information of Result

Type of Conformer	Anti 2
Method	Optimization to a minimum
Basis Set	HF/3-21G
Memory Limit	250 MB
Total Energy	-231.69253526 a.u.
Current Symmetry Group	Ci

3. Validity of Result

3.1 Real Output

        Item               Value     Threshold  Converged?
Maximum Force            0.000031     0.000450     YES
RMS     Force            0.000009     0.000300     YES
Maximum Displacement     0.001718     0.001800     YES
RMS     Displacement     0.000379     0.001200     YES
Predicted change in Energy=-4.697986D-08
Optimization completed.
   -- Stationary point found.

Both force and displacement converged. This confirms the optimization is successful and the resultant molecule is in its energy minimum.

3.2 Frequency Analysis

Frequency analysis carried out from the previously optimized file shows all the frequencies have positive values (from 71.44 cm^-1 to 3385.44 cm^-1), therefore double confirms the optimization is correct.

4. File Link

To access the .log file of optimization, click here; for the .log file of frequency analysis, click here.

To view the screenshot of the calculation summary table, click here; click here for symmetry information.

Optimization of Predicted Most Stable Conformer of 1,5-hexadiene (gauche)

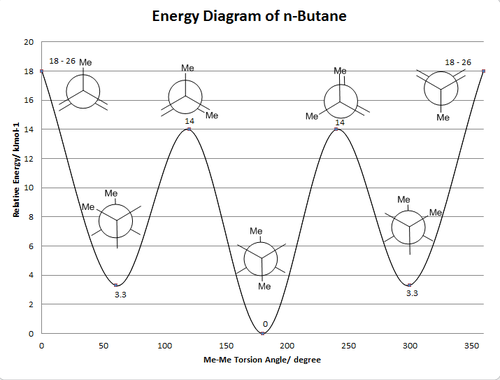
Normally, the gauche conformation is supposed to be energetically less stable than the anti-peri planar conformation, i.e., higher in energy. This is due to the van der Waals strain between two large R groups which are closer to each other in gauche conformers. Newman Projections for both structures are shown below:

As in the gauche conformation, to large R groups are only 60^o apart from each other while in anti-peri planar conformation they are 180^o from each other. The repulsion between R groups is thus larger in gauche conformation and energy barrier results.

The energy diagram of conformers of n-butane is drawn below according to the quantitative research by D. Nasipuri. It is clearly stated that the most stable conformer has anti structure.

However, in 1,5-hexadiene, there is analogue resulted from pi-pi interaction between R groups. An illustration of the overlapping is shown as following.

The pi-pi overlapping provides extra stabilization towards the gauche conformer, therefore one of the gauche conformer lies lower in energy than all the anti-peri planar conformers.

In comparison, there is an energy profile diagram for 1,5-hexadiene presented by Benjamin W as well which matches the experimental values.

1. Optimized Gauche Structure

test molecule

2. Key Information of Result

Type of Conformer	Gauche 3
Method	Optimization to a minimum
Basis Set	HF/3-21G
Memory Limit	250 MB
Total Energy	-231.69266121 a.u.
Current Symmetry Group	C1

3. Validity of Result

3.1 Real Output

        Item               Value     Threshold  Converged?
Maximum Force            0.000029     0.000450     YES
RMS     Force            0.000006     0.000300     YES
Maximum Displacement     0.001012     0.001800     YES
RMS     Displacement     0.000378     0.001200     YES
Predicted change in Energy=-1.305867D-08
Optimization completed.

Both force and displacement converged. This confirms the optimization is successful and the resultant molecule is in its energy minimum.

3.2 Frequency Analysis

Frequency analysis carried out from the previously optimized file shows all the frequencies have positive values (from 74.55 cm^-1 to 3386.85 cm^-1), therefore double confirms the optimization is correct.

4. File Link

To access the .log file of optimization, click here; for the .log file of frequency analysis, click here

To view the screenshot of the calculation summary table, click here; click here for symmetry information.

Reoptimization of Anti 2 Conformer of 1,5-hexadiene

1. Reoptimized Anti 2 Structure

test molecule

2. Key Information of Result

Type of Conformer	Anti 2
Method	Optimization to a minimum
Basis Set	B3LYP/6-31G(d)
Memory Limit	250 MB
Total Energy	-234.61171035 a.u.
Current Symmetry Group	Ci

3. Validity of Result

3.1 Real Output

        Item               Value     Threshold  Converged?
Maximum Force            0.000016     0.000450     YES
RMS     Force            0.000007     0.000300     YES
Maximum Displacement     0.000258     0.001800     YES
RMS     Displacement     0.000088     0.001200     YES
Predicted change in Energy=-1.650727D-08
Optimization completed.
   -- Stationary point found.

Both force and displacement converged. This confirms the optimization is successful and the resultant molecule is in its energy minimum.

3.2 Frequency Analysis

Frequency analysis carried out from the previously optimized file shows all the frequencies have positive values (from 74.29 cm^-1 to 3233.90 cm^-1), therefore double confirms the optimization is correct.

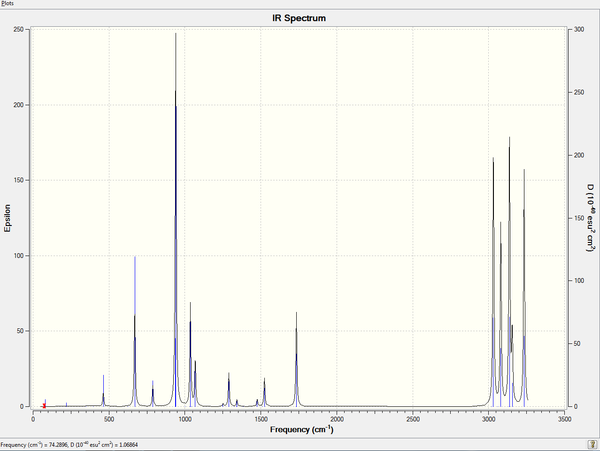
3.3 IR Spectrum

The predicted IR spectrum may differ with experimental results as most of the IR machines are not able to distinguish between gauche and anti structures which interchange quickly. Generally the experimental IR spectrum will give an indication on the 'average' of the mixture of all conformers. An experimental spectrum done by Dow Chemical Company in 1967 is found in the online data base.

• This is the original scan of the hardcopy of spectrum, for more details on the provider, as well as digitized spectrum, this website can be accessed.

In general, the experimental frequancies tend to have smaller wavenumbers: for example, there are 4 intensive peaks at the region around 3000 - 3300 cm^-1, which have been shifted to 2800 - 3100 cm^-1 in experiment. The features, including intensity and relative positions of the peaks do not change from prediction to experimental, indicating that they are based on the same molecule.

Another reason for the shift of peaks might be the difference in temperature. The prediction in Gaussian was made at 298.15 K while the real temperature of the experimental spectrum is not obtainable. However, this fact will not affect the frequencies in such a great extent (ca. 200 - 300 cm^-1).

The experimental spectrum is also based on old techniques. Nowadays, spectrometers have been developed to be much more sensitive and accurate, therefore, the distinguishment between gauche and anti conformers may be achieved.

4. File Link

To access the .log file of optimization, click here; for the .log file of frequency analysis, click here.

To view the screenshot of the calculation summary table, click here; click here for symmetry information.

Result and Discussion

1. General Geometry Data

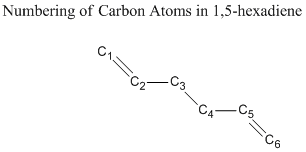
Major bond lengths, bond angles, as well as dihedral angles calculated by different methods are listed and compared with literature values in the following session. Numbering of carbon atoms in 1,5-hexadiene is shown below.

Parameter	HF/3-21G	B3LYP/6-31G(d)	Literature Value
C1=C2 Bond Length/ Å	1.3162	1.3335	1.3412
C2-C3 Bond Length/ Å	1.5089	1.5042	1.5077
C3-C4 Bond Length/ Å	1.5529	1.5481	1.5362
C-H Bond Length/ Å	1.074	1.0997	1.1077
C2-C3-C4 Bond Angle	111.3464o	112.6749o	111.0o
C1=C2-C3 Bond Angle	124.8130o	121.8691o	122.5o
C2=C1-H Bond Angle	121.8244o	121.6515o	120.4o
C3-C2-H Bond Angle	119.6736o	118.981o	118.4o
H-C3-H Bond Angle	107.7129o	106.6561o	107.1o
C2-C3-C4-C5 Dihedral Angle	-179.9890o	-180.0000o	-178.3o

The literature value is based on the experimental measurement of an average of anti-peri planar conformers. Therefore, the dihedral angle is not exactly -180^o as theoretically it should be. Generally, the B3LYP/6-31G(d) method is more accurate than the HF/3-21G method as the optimized bond angles and bond lengths become much closer to literature and dihedral angle becomes exactly -180^o. The HF/3-21G method usually gives bond lengths values which are smaller than literature and bond angle values larger than literature. The B3LYP/6-31G(d) makes correction towards the right magnitude, making the data more similar to literature.

The dipole moment (0.0003 Debye from HF/3-21G method and 0.0000 Debye from B3LYP/6-31G(d) method) is very small due to the slight difference between C and H atoms.

2. Thermochemistry

Different energies under certain vibrational temperatures are calculated as well. All the calculations are set in pressure of 1.0 atm and temperatures are varied as tabulated below.

Type of Energy	B3LYP/6-31G(d) at 298.15 K/ a.u.	B3LYP/6-31G(d) at 0 K/ a.u.	HF/3-21G at 298.15 K / a.u.	HF/3-21G at 0 K/ a.u.	Description
Sum of electronic and zero-point Energies	-234.469204	-234.468766	-231.539541	-231.539541	potential energy at 0 K including the zero-point vibrational energy (E = Eelec + ZPE)
Sum of electronic and thermal Energies	-234.461857	-234.461430	-231.532567	-231.532567	energy at 298.15 K and 1 atm of pressure which includes contributions from the translational, rotational, and vibrational energy modes at this temperature (E = E + Evib + Erot + Etrans)
Sum of electronic and thermal Enthalpies	-234.460913	-234.460486	-231.531623	-231.531623	additional correction for RT (H = E + RT)
Sum of electronic and thermal Free Energies	-234.500777	-234.500328	-231.570913	-231.570913	entropic contribution to the free energy (G = H - TS)
Electronic Energy	-234.611710	-234.611710	-231.692536	-231.692536	Sum of electronic and zero-point energies with zero-point correction

The electronic energies modified within same method stay same, which is -234.611710 a.u. from B3LYP/6-31G(d) method (-234.611710 a.u. as provided in script) and -231.692536 a.u. from HF/3-21G method (-231.692535 a.u. as provided). This ensures the correction of optimization and shows a difference between different methods, which indicates that comparison between different methods is meaningless due to the large energy difference (2.919175 a.u. = 1831.8086 kcal/mol in this case).

The more accurate B3LYP/6-31G(d) method provides a lower electronic energy, which indicates the structure is further stabilized.

3. Symmetry

Conformer	Symmetry Point Group of .chk File	Literature Point Group	Symmetry Point Group of .log File
Anti 1	C2	C2	C1
Anti 2	Ci	Ci	C1
Gauche 3	C1	C1	C1
Gauche 4	C2	C2	C1

All the optimizations have been carried out correctly because all symmetry point groups match well with literature. It is noticed that all symmetry has been switched to C1 in the final stage. This is not an error because the program turns off all symmetries in order to get an energy minimum.

Optimization of an Allyl Fragment

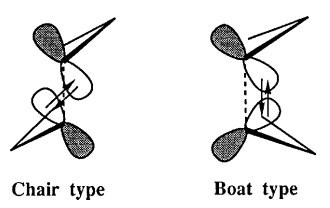
Both chair and boat transition state can be recognized of a combination of two identical allyl (C₃H₅) fragments.

and

C_2h Chair Transition State and C_2v Boat Transition State

Therefore, it is important to make sure allyl fragment is successfully optimized before investigating into the actual transition states to minimize all possible sorts of errors.

1. Optimized Allyl Fragment

test molecule

2. Key Information of Result

Method	HF/3-21G
Memory Limit	250 MB
Total Energy	-115.82304010 a.u.

3. File Link

To access to the .log file of optimization, click here; click here for screenshot of calculation summary.

Optimization of the 'chair' Transition State

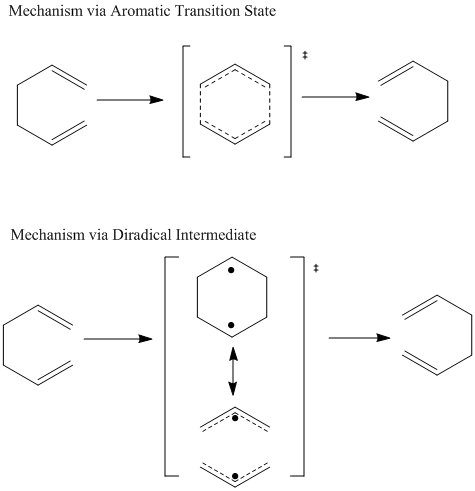
The mechanism via 'chair' transition state has been originally recognized as energetically and structurally equivalent to a diradical. This respect the uncharged nature of the transition state and can be rationalized via the simple combination of two allyl fragments. In this type of mechanism, bond breaking and bond making processes are considered as happening separately in two steps via the diradical intermediate. One of the possible mechanism is suggested as following.

However, later research by Zimmerman et al suggested mechanism in another point of view which is widely accepted that it is a concerted process via a homoaromatic transition state rather than diradical intermediate which undergoes the degenerate Cope rearrangement with a very small activation barrier. This transition state is recognized as an aromatic system with high extent of electron delocalization. The mechanism is also shown below.

Unlike other typical sigmatropic rearrangement such as [1,3] carbon shift or [1,5] hydrogen shift, the [3,3] hydrogen shift undergoes the migration of an allyl group, rather than a single atom. It is a 6 pi electron (4+2) system. When promoted by light, the reaction is thermally allowed via Hückel topology with suprafacial components.

Initially, the chair transition state is made up from two previously optimized allyl fragments with the distance between terminal carbons adjust to exactly 2.2 Å shown as following. It was then optimized in three different approaches in order to allow comparison and confirmation of possible mechanism.

First Approach: Optimization with Berny Algorithm

As introduced in the Gaussian 09 User's Reference, Berny algorithm is one of the default method developed by Bernhard Schlegel. The basic idea of this method is to predict the most stable structure from the forces acting on the atoms together with the Hessian matrix. In order to reduce the time required to carry out full calculation, the method constructs an approximate Hessian at starting of optimization. This effectively makes optimization shorter in time, but sometimes leads to inaccurate results, depends on how well the approximation can be made.

1. Optimized Chair Transition State

test molecule

2. Key Information of Result

Type of Transition State	Chair
Method	Optimization to a TS (Berny)
Basis Set	HF/3-21G
Keyword	Opt=NoEigen
Total Energy	-231.61932243 a.u.
Number of Imaginary Frequency	1
Wavenumber of Imaginary Frequency	-817.97 cm-1

3. Vibration Mode of Imaginary Frequency

4. File Link

To access to the .log file of optimization, click here; click here for screenshot of calculation summary.

Second Approach: Frozen Coordinates Method

The frozen coordinates provide a prior before optimization to set the numerical values of certain parameters of atoms frozen. In this case, both the bond breaking and bond making distances have been set to exactly 2.2 Å. If not set, the parameters of atoms might be changed during optimization to give the energetically minimized structure, which might vary from literature. This method is usually used when literature parameters such as bond angle and bond length is known and the guess structure does not vary too much from literature.

1. Key Information of Result

Type of Transition State	Chair
Method	Optimization to a TS (Berny)
Basis Set	HF/3-21G with Freeze Coordinate
Keyword	Opt=ModRedundant
Total Energy	-231.61932244 a.u.
Number of Imaginary Frequency	1
Wavenumber of Imaginary Frequency	-817.97 cm-1

2. Vibration Mode of Imaginary Frequency

3. File Link

To access to the .log file of optimization, click here; click here for screenshot of calculation summary.

Third Approach: Calculation with Derivative and IRC

Given the structure of transition state being optimized correctly, it does not mean that mean that the resultant structure is the actual connection between reactant and product. Intrinsic reaction coordinate (IRC), which is defined as the minimum energy reaction pathway (MERP) in mass-weighted cartesian coordinates between the transition state of a reaction and its reactants and products, will be used in this part. It can be thought of as the path that the molecule takes moving down the product and reactant valleys with zero kinetic energy.

In this stage, 50 is set to be the number of points and force constant is always calculated. Additionally, since the reaction coordinate is symmetric for chair conformer, only calculation on the forward direction is carried out whereas generally both directions will be taken into consideration.

1. Key Information of Result

Type of Transition State	Chair
Method	Optimization to a TS (Berny)
Basis Set	HF/3-21G with Derivative
Keyword	Opt=ModRedundant
Total Energy	-231.61932200 a.u.
Number of Imaginary Frequency	1
Wavenumber of Imaginary Frequency	-818.03 cm-1

To access to the .log file of optimization, click here; click here for screenshot of calculation summary.

2. Vibration Mode of Imaginary Frequency

3. IRC Calculation

Type of Transition State	Chair
Method	IRC
Basis Set	HF/3-21G
Number of Points	50
Direction	Forward Only
Energy of Last Point	-231.69157867 a.u.

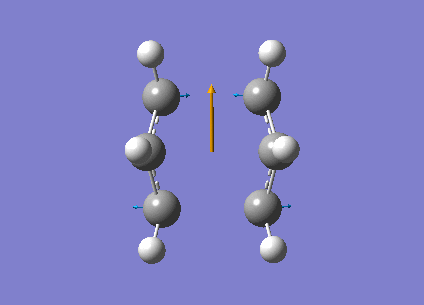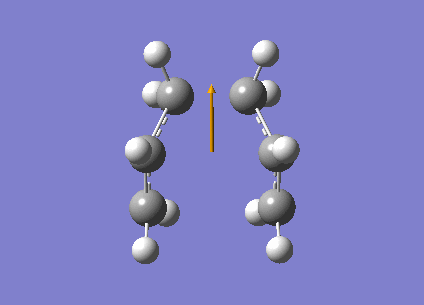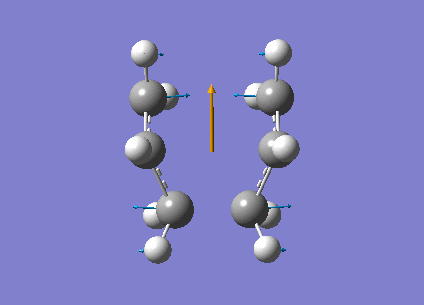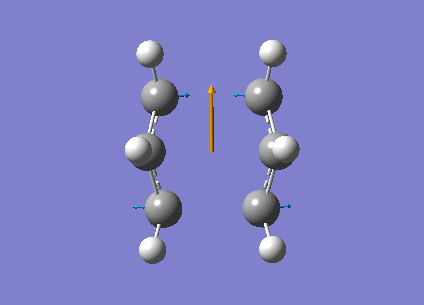
Modified Transition State:

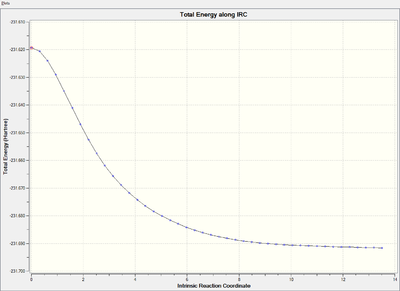
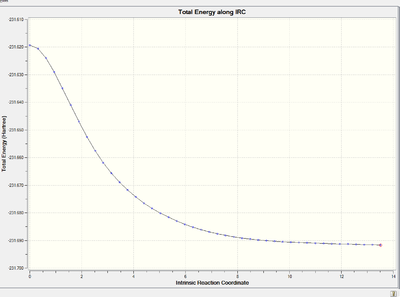
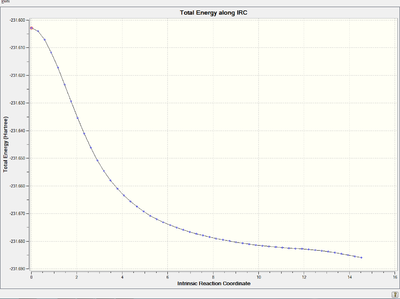
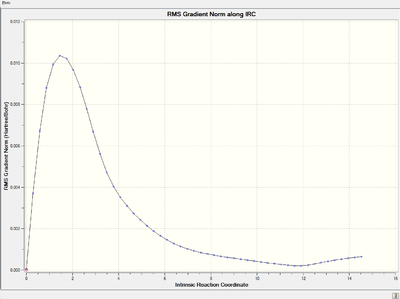
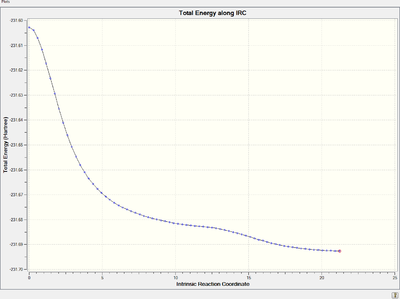
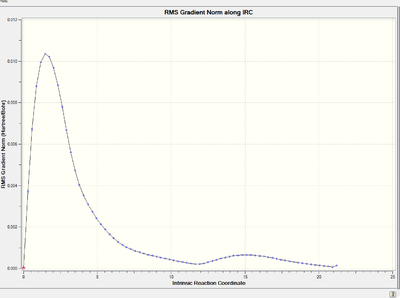
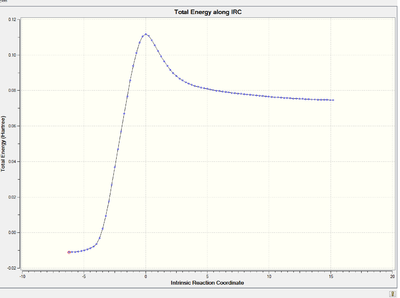
Energy and RMS gradient graph:

It is clear that the RMS gradient converges to nearly 0, which confirms that it is an energy minimum.

To view the .log file of IRC calculation, click here; for the screenshot of IRC calculation summary, click here.

However, the initial IRC calculation only shows a trend of converging to an energy minimum, i.e., the RMS gradient is supposed to reach 0 at last. Therefore, further modification are made to give a more accurate and reliable result.

There are three methods that can be investigated in order to improve the accuracy of IRC calculation:

Method 1: optimization to minimum with the last point of IRC calculation. This is the most time-effective approach but exists a risk of getting far away from local minimum due to the inaccuracy involved in the last point.

Method 2: redoing IRC calculation with larger number of points until a minimum is reached. This approach requires more time but gives more reliable results.

Method 3: redoing IRC calculation, computing force constant at each step. This approach ends up with the most time-consuming but most reliable results. However, it has certain limitation that might not work well for larger systems.

Method 1. Optimization of the IRC Endpoint

Type of Transition State	Chair
Method	Optimization to Minimum
Basis Set	HF/3-21G
Total Energy	-231.69166702 a.u.

Click here for .log file of optimized IRC endpoint; and here for screenshot of the calculation summary.

Method 2. IRC Calculation with Larger Number of Stpes

Type of Transition State	Chair
Method	IRC
Basis Set	HF/3-21G
Number of Points	150
Direction	Forward Only
Energy of Last Point	-231.69157867 a.u.

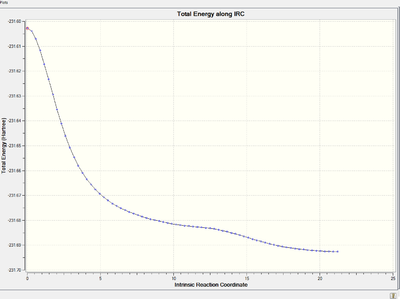
Energy and RMS gradient graph:

To access to the .log file of IRC calculation, click here.

Reoptimization using B3LYP/6-31G* Level of Theory

1. Key Information of Result

Type of Transition State	Chair
Method	Optimization to a TS (Berny)+ Frequency Analysis
Basis Set	B3LYP/6-31G*
Total Energy	-234.55698303 a.u.
Number of Imaginary Frequency	1
Wavenumber of Imaginary Frequency	-565.53 cm-1

2. Validity of Result

2.1 Real Output

        Item               Value     Threshold  Converged?
Maximum Force            0.000027     0.000450     YES
RMS     Force            0.000005     0.000300     YES
Maximum Displacement     0.000108     0.001800     YES
RMS     Displacement     0.000035     0.001200     YES
Predicted change in Energy=-5.311302D-09
Optimization completed.
   -- Stationary point found.

All the parameters converged to confirm there is an energy minimum.

Comparing to the output of previous optimization, an obvious improvement has been made. Theoretically all the force parameters are supposed to be exactly 0 in the perfect case. The maximum of force decreased from 0.000058 to 0.000027, the RMS force has been reduced from 0.000008 to 0.000005, which is nearly ideal. Furthermore, maximum of displacement parameter experienced a significant decrease from 0.000640 to 0.000108 and the RMS displacement parameter reduced from 0.000113 to 0.000035. These all proves that the optimization has reaches a more accurate point in the B3LYP/6-31G* method.

2.2 Frequency Analysis

Only one imaginary frequency appears as expected. However, there is a significant change in frequency from -818 cm^-1 to -565.53 cm^-1 which is analogue.

The vibration mode at -565.53 cm^-1 is modified as below:

3. File Link

To access to the .log file of optimization, click here; for the screenshot of calculation summary, click here.

Result and Discussion

1. General Geometry Data

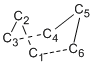
The numbering of carbon atoms of the chair transition state is shown below.

Parameter	HF/3-21G	B3LYP/6-31G(d)	Literature Value
C1-C2 Distance/ Å	2.3736	2.3736	1.599
C4-C5 Distance/ Å	2.4452	2.4452	1.899
C2-C3 and C5-C6 Bond Length/ Å	1.4075	1.4075	1.474
C3-C4 and C1-C6 Bond Length/ Å	1.4075	1.4075	1.382
C-H Bond Length/ Å	1.0886	1.0886	1.110
C4-C5-C6 Bond Angle	119.7048o	112.4944o	113.4o
C2-C3-C4 Bond Angle	107.4615o	103.6352o	106.4o
Dihedral Angle	64.0448o	65.1817o	Not Available

The optimization results an unaccurate prediction of the structure of transition states comparing to literature. The most biased parameter is the interfragmental distance which is assumed to be around 2.2 Å manually, where experiments suggest values of 1.599 Å and 1.899 Å respectively.

However, there are other researches supporting the interfragmental distance to be roughly 2.2 Å such as the study of cope rearrangement transition state by Paul G. Wenthold.

2. Thermochemistry

Different energies under certain vibrational temperatures are calculated as well. All the calculations are set in pressure of 1.0 atm and temperatures are varied as tabulated below.

Type of Energy	B3LYP/6-31G(d) at 298.15 K/ a.u.	B3LYP/6-31G(d) at 0 K/ a.u.	HF/3-21G at 298.15 K / a.u.	HF/3-21G at 0 K/ a.u.
Sum of electronic and zero-point Energies	-234.414929	-234.411622	-231.466697	-231.466701
Sum of electronic and thermal Energies	-234.409008	-234.405160	-231.461337	-231.461341
Sum of electronic and thermal Enthalpies	-234.408064	-234.404216	-231.460393	-231.460397
Sum of electronic and thermal Free Energies	-234.443814	-234.441257	-231.495203	-231.495207
Electronic Energy	-234.556983	-234.554464	-231.619323	-231.619323

Most of the data makes excellent agreement with the data provided on script. However, there seems to be a problem in calculation of B3LYP/6-31G(d) at 0 K since the electronic energy differ in a large extent with literature. Also, the B3LYP/6-31G(d) method gives a lower total energy, which indicates that this basis set provides more stabilized structure than the HF/3-21G basis set.

Optimization of the 'boat' Transition State

The 'boat' transition state provides another route of reaction mechanism of the [3,3] sigmatropic rearrangement. It is accepted that the transition state undergoes a six centered 'roof' like structure as W.Von E.Doering suggested.

It also can be recognized as the diradical intermediate via a two step mechanism similar to the chair transition state.

First Attempt: Optimization from Anti 2 Conformer

In the first stage, optimization to TS (QST2) is used, which allows the optimization of the transition state given reactant and product specified. However, since it simply transfers the reactant to product without and consideration in the bond rotation, it could be inaccurate or even cause errors during optimization.

The previously optimized anti 2 conformer (Ci symmetry) is assumed to be both the reactant and product in this case. However, since the numbering of carbon atoms definitely change during reaction, it is necessary to set up the labels of each atoms manually as below.

However, the optimization has apparently failed, giving a transition state similar to 'chair' structure as shown below.

The reason is that the structure of anti 2 conformer differs from the 'boat' transition state to a large extent. In order to rationalize optimization, modification of structures of both reactant and product need to be carried out in the next session.

Second Attempt: Optimization from Modified Reactant and Product

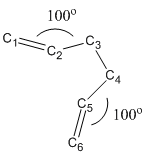
In order to locate the 'boat' transition state more precisely, modification of the structure is made as follow. The bond angle between C2-C3-C4 as well as C3-C4-C5 are made 100^o and the dihedral angle between C2-C3-C4-C5 is made 0^o.

1. Optimized Boat Transition State

test molecule

2. Key Information of Result

Type of Transition State	Boat
Basis Set	HF/3-21G
Method	Optimization to TS (QST2)
Total Energy	-231.60280247 a.u.
Number of Imaginary Frequency	1
Wavenumber of Imaginary Frequency	-839.94 cm-1

3. Vibration Mode of Imaginary Frequency

4. Validity of Result

4.1 Real Output

        Item               Value     Threshold  Converged?
Maximum Force            0.000073     0.000450     YES
RMS     Force            0.000014     0.000300     YES
Maximum Displacement     0.001445     0.001800     YES
RMS     Displacement     0.000510     0.001200     YES
Predicted change in Energy=-1.787723D-08
Optimization completed.
   -- Stationary point found.

All the parameters converged.

4.2 Frequency Analysis

Only one imaginary frequency appears at -839.94 cm^-1 to show the existence of a transition state.

5. File Link

To access to the file link of .log file of optimization, click here; for a screenshot of calculation summary, click here.

IRC Calculation

In order to obtain more detailed information on the reaction pathway along the energy surface of minimum, IRC calculation is carried out on the optimized 'boat' transition state.

Key Information of Calculation

Type of Transition State	Boat
Basis Set	HF/3-21G
Method	IRC
Number of Points	50
Direction	Forward only
Energy of Last Point	-231.68596311 a.u.

Modified transition state:

Energy and RMS gradient graph:

To access to the .log file of IRC calculation, click here;.

In order to locate the energy minimum and improve the accuracy of previous IRC calculation, same methods are investigated based on the IRC calculation as what have been done on the 'chair' transition state.

Method 1. Optimization of IRC Last Point

Type of Transition State	Boat
Method	Optimization to a minimum
Total Energy	-231.69266122 a.u.

For the .log file of optimization of IRC last point, click here and click here for a screenshot of the calculation summary.

Method 2. IRC Calculation with Larger Number of Steps

Type of Transition State	Boat
Basis Set	HF/3-21G
Method	IRC
Number of Points	150
Direction	Forward only
Energy of Last Point	-231.69261259 a.u.

Energy and RMS gradient graph:

For the .log file of 150 step IRC calculation, click here

Method 3. Calculating Force Constant at Each Step

Type of Transition State	Boat
Basis Set	HF/3-21G
Method	IRC
Number of Points	150
Direction	Forward only
Energy of Last Point	-231.69261259 a.u.

Energy and RMS gradient graph:

For the .log file of 150 step IRC calculation, click here

Reoptimization using B3LYP/6-31G* Level of Theory

1. Reoptimized Boat Transition State

test molecule

2. Key Information of Result

Type of Transition State	Boat
Method	Optimization to a TS (Berny)+ Frequency Analysis
Basis Set	B3LYP/6-31G*
Total Energy	-234.54309304 a.u.
Number of Imaginary Frequency	1
Wavenumber of Imaginary Frequency	-530.57 cm-1

3. Validity of Result

3.1 Real Output

        Item               Value     Threshold  Converged?
Maximum Force            0.000017     0.000450     YES
RMS     Force            0.000004     0.000300     YES
Maximum Displacement     0.000760     0.001800     YES
RMS     Displacement     0.000195     0.001200     YES
Predicted change in Energy=-3.598582D-08
Optimization completed.
   -- Stationary point found.

All parameters converged as gave values closer to zero in comparison of the previously optimized molecule. This confirms the success of optimization with a more accurate method.

3.2 Frequency Analysis

Only one imaginary frequency is found, indicating the existence of a transition state. The vibration mode of the imaginary frequency is shown as following.

4. File Link

To access the .log file of optimization, click here and click here for a screenshot of calculation summary.

Result and Discussion

1. General Geometry Information

The numbering of carbon atoms of the boat transition state is shown below.

Parameter	HF/3-21G	B3LYP/6-31G(d)	Literature Value
C1-C6 Distance/ Å	2.1403	2.6536	1.849
C3-C4 Distance/ Å	2.1398	2.4681	1.573
C1-C2 and C5-C6 Bond Length/ Å	1.3814	1.3932	1.392
C3-C4 and C1-C6 Bond Length/ Å	1.3814	1.3933	1.469
C-H Bond Length/ Å	1.0739	1.0870	1.113
C2-C1-C6 Bond Angle	114.6801o	111.6357o	109.9o
Dihedral Angle	-64.7305o	-64.1740o	Not Available

Similarly to the chair transition state, the optimization gives good agreement with literature structure despite the interfragment distances which differs at around 0.6 Å. As agreed previously, the B3LYP/6-31G(d) basis set generally tends to provide a more accurate and more energetically stabilized structure than the HF/3-21G basis set.

2. Thermochemistry

Different energies under certain vibrational temperatures are calculated as well. All the calculations are set in pressure of 1.0 atm and temperatures are varied as tabulated below.

Type of Energy	B3LYP/6-31G(d) at 298.15 K/ a.u.	B3LYP/6-31G(d) at 0 K/ a.u.	HF/3-21G at 298.15 K / a.u.	HF/3-21G at 0 K/ a.u.
Sum of electronic and zero-point Energies	-234.402339	-234.402339	-231.450928	-231.450928
Sum of electronic and thermal Energies	-234.396005	-234.396005	-231.445299	-231.445299
Sum of electronic and thermal Enthalpies	-234.395061	-234.395061	-231.444355	-231.444355
Sum of electronic and thermal Free Energies	-234.431748	-234.431748	-231.479774	-231.479774
Electronic Energy	-234.543093	-234.543093	-231.602802	-231.602802

All the thermochemistry data matches well with script and the same electronic energy is obtained at different temperatures using same method. This confirms the success of analysis.

As the temperature decreases, there is a slight decrease of all the energy parameters due to the reduction of thermal energy. However, it is not obvious and makes no affection on the total electronic energy.

Result and Discussion

Reaction Mechanism

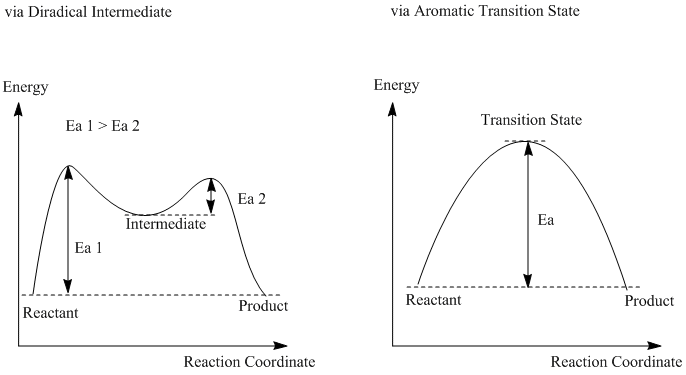
As discussed in previous sessions, two types of mechanisms have been suggested for the Cope rearrangement, namely via 'diradical intermediate' and 'aromatic transition state' respectively. Although in this experiment, only structures of transition states have been analysed and discussed, it is still meaningful to discuss both case.

Mechanism of both are drawn as below.

The resultant energy diagram for this reaction is therefore different as shown below.

Since in this certain reaction of 1,5- hexadiene, reactant and product have exactly the same structure, there is no energy difference between starting point and end point of reaction path.

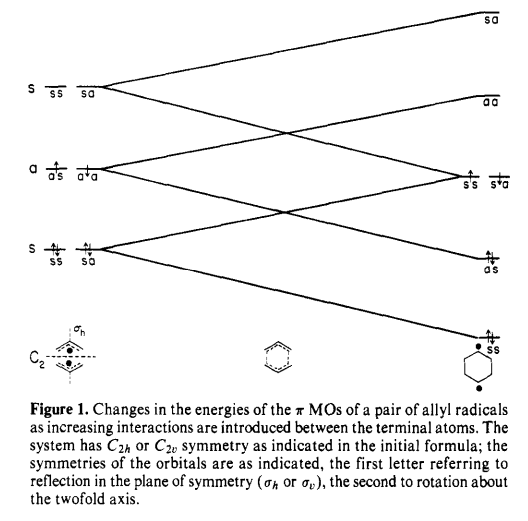
There are already many researches that confirmed the extra stability of the aromatic transition state rather than diradical intermediate. A study of the mechanism of the Cope rearrangement has been done by Michael J. S. Dewar, suggesting the change in total energy from two separate radical species to the delozalized aromatic system from the molecular orbital's point of view. As the tendency of delocalization occurs and the transition state becomes aromatic, extra stabilization is produced in process of increased interaction between terminal carbon atoms. There is an illustration from his review.

It is also confirmed that the chair and boat transition states are distinguishable in energy as well. Though it is possible for the Cope rearrangement to proceed via either transition state, the boat structure is slightly higher in energy than chair structure. The reason is that the magnitude of relative energy is associated with the energy involved in bond breaking and bond making processes (in this case, both bonds of making and breaking is the sigma bond between terminal carbons). In one research of Shogo Sakai, the orbital interaction of both transition is drawn as following.

It clearly illustrates that in boat transition state, the bonding making and breaking characters become more sensitive toward sigma bond length between terminal carbon atoms. Therefore, the stain of geometry is introduced and boat structure lies slightly higher in energy than the chair structure in theory.

The calculations done by Gaussian also make agreement with the theoretical prediction.

Type of Transition State	Chair	Boat
Total Energy using HF/3-21G Basis Set	-231.61932243 a.u.	-231.60280247 a.u.
Total Energy using B3LYP/6-31G* Basis Set	-234.55698303 a.u.	-234.54309304 a.u.

In both method, the chair transition state is stabilized by ca. 0.015 a.u. comparing to boat transition state.

Activation Energy

Activation energy refers to the minimum energy required to start a chemical reaction. For example, it can be the energy difference between reactant and the most unstable transition state through a reaction path. In order to obtain a reasonable rate of reaction, some molecules in the system must have energy equal or higher than activation energy.

The symbolization of activation energy is usually 'Ea'.

In this experiment, since it has been confirmed that only transition states should be taken into consideration, activation energy of this [3,3] sigmatropic rearrangement is calculated based on the energy difference from reactant/ product and both transition states. The results are tabulated as following.

Type of Basis Set	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Experimental
Temperature	at 298.15 K	at 0 K	at 298.15 K	at 0 K	at 0 K
Ea(Chair) /kcalmol-1	44.7	45.7	33.2	34.1	33.5 ± 0.5
Ea(Boat) /kcalmol-1	54.7	55.6	41.3	42.0	44.7 ± 2.0

It is clear that the B3LYP/6-31G* basis set shows a higher level of accuracy which tends closer to the experimental value for both activation energies of chair and boat transition states. The HF/3-21G basis set results in a bias of roughly 11 - 12 kcal/mol for both transition state, which is quite large.

However, there is still a slight different from experimental (ca. 1.5 kcal/mol for chair transition state and ca. 3.0 kcal/mol for boat transition state).

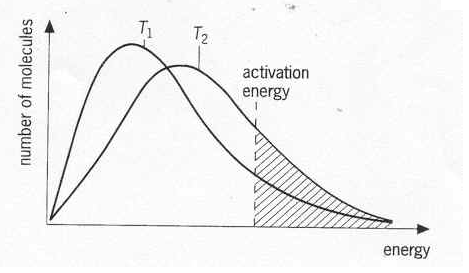
As temperature decreases, there is a tendency for activation energy to increase. This phenomenon can be explained as the increase in temperature brings up the average kinetic energy of molecules. The effect of change in temperature only exists on molecules that have energy beyond the energy barrier of reaction. Therefore, as temperature increases, more molecules will be activated and participate in the reaction. This results both a decrease in activation energy and an increase in reaction rate. An illustration is drawn to give a more direct explanation.

Source of picture: http://www.webchem.net/notes/how_far/kinetics/rate_factors.htm

(T2 is higher than T1)

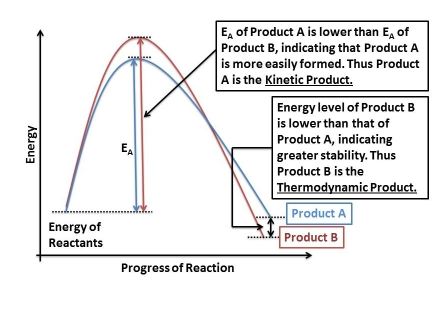
Also, since both the reactant and product have been assumed to have exactly the same structure and same total energy (anti 2 conformer in this case), the difference between thermodynamic and kinetic products has not been taken into consideration.

Source of picture: http://pharmaxchange.info/press/2011/03/thermodynamic-product-vs-kinetic-product-with-examples/

The thermodynamic product is energetically more stable but requires a higher activation energy. In contrast, the kinetic product is energetically less stable but has energy barrier that is easier to overcome. Corresponding to the results above, it is clear that the kinetic process is via chair transition state and the thermodynamic process is via boat transition state.

In this certain reaction, the kinetic product might be any of the anti conformers while the thermodynamic product might be the gauche 3 conformer which lies lowest in energy among all the eight conformers.

Accordingly, at low temperature, it is likely to proceed via chair transition state with a faster reaction; given high temperature and long reaction time, mechanism via boat transition state becomes more likely to happen.

Example b: The Diels Alder Cycloaddition

Cycloaddition reaction is categorized in pericyclic reactions. One typical [4+2] cycloaddtion, named Diels Alder Reaction, has been developed and utilized for decades since last century. It not only allowed further detailed studies into this certain type of cycloaddition reaction, but also afforded numerous new solutions toward organic synthesis.

The mechanism involves the sigma bond forming through conjugation of HOMO/LUMO of one reactant and HOMO/LUMO of the other reactant. Weather the interaction between HOMO/LUMO is allowed gives indication on weather the reaction is allowed, which depends greatly on the nature of reacting species.

In this experiment, studies of transition states in Diels Alder reactions will be achieved using quantum mechanic approaches. Unlike in analysis of cope rearrangement where Hartree-Fock and DFT have been developed, the AM1 semi-empirical molecular orbital method will be used in investigation. This method performs better in locating transition states, as well as being more effective, but bears the disadvantage of poor prediction on larger systems.

Two Diels Alder reactions will be covered in the following sessions, one of ethylene and cis-butadiene, the other one of cyclohexa-1,3-diene and maleic anhydride.

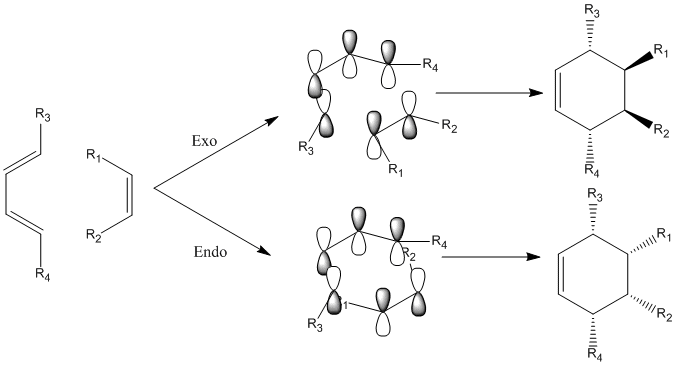
Reaction Between Ethylene and Cis-Butadiene

In this session, one of the simplest case of Diels Alder reaction will be investigated between ethylene, which performs as dieneophile, and cis-butadiene, which performs as diene. It only involves in unsubstituted carbons with even sized atomic orbitals.

The reaction scheme is drawn as following.

Two sigma bonds have been formed through terminal carbons, resulting the formation of cyclic product. The process is generally considered as being concerted and detailed mechanisms will be investigated later in the discussion session.

Optimization of Reactants

Firstly, both the reactants are optimized and results are shown as below.

1. Optimization of Cis-butadiene

1.1 Optimized Cis-butadiene

test molecule

1.2 Key Information of Result

Molecule	Cis-butadiene
Method	Optimization to a minimum
Basis Set	AM1 semi-empirical MO
Total Energy	0.04879719 a.u.

1.3 File Link

To access the .log file of optimization, click here; click here for a screenshot of the calculation summary.

2. Optimization of Ethylene

2.1 Optimized Ethylene

test molecule

2.2 Key Information of Result

Molecule	Ethylene
Method	Optimization to a minimum
Basis Set	AM1 semi-empirical MO
Total Energy	0.02619028 a.u.

1.3 File Link

To access the .log file of optimization, click here; click here for a screenshot of the calculation summary.

Analysis of Transition States

Optimization of Guess Transition State using AM1 Semi-Empirical MO

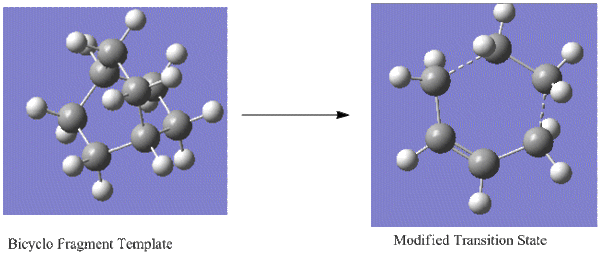
The transition state is modified based on a bicyclo fragment by removing the CH₂-CH₂ unit and modifying intergragmental distance to 2.2 Å, which is suggested by Suarez, D. The modification is shown as following.

1. Optimized Transition State

test molecule

2. Key Information of Result

Method	Optimization to TS(Berny)
Basis Set	AM1 semi-empirical MO
Key Word	Opt=NoEigen
Total Energy	0.1165470 a.u.
Number of Imaginary Frequency	1
Wavenumber of Imaginary Frequency	-957.06 cm-1

The key word 'Opt=NoEigen' is added in order to prevent the Gaussian program from crushing if more than one imaginary frequencies is obtained during optimization.

3. Validity of Result

3.1 Real Output

        Item               Value     Threshold  Converged?
Maximum Force            0.000127     0.000450     YES
RMS     Force            0.000022     0.000300     YES
Maximum Displacement     0.001060     0.001800     YES
RMS     Displacement     0.000285     0.001200     YES
Predicted change in Energy=-5.322391D-08
Optimization completed.
   -- Stationary point found.

All parameters converged to confirm an energy minimum has been reached.

3.2 Frequency Analysis

Only one imaginary frequency at -957.06 cm^-1, indicating the existence of transition state. The vibration mode for this frequency is displayed as below.

4. File Link

To access the .log file of optimization, click here; to view a screenshot of the calculation summary, click here.

IRC Calculation of Transition State using AM1 Semi-Empirical MO

1. Optimized Transition State

test molecule

2. Key Information of Result

Method	IRC
Basis Set	AM1 semi-empirical MO
Key Word	Opt=NoEigen
Number of Steps	100
Direction	Both Directions
Total Energy of Last Point	0.07462831 a.u.

Modified transition state:

Energy and RMS gradient graph:

3. File Link

To access the .log file of IRC calculation, click here; click here for screenshot of calculation summary.

Optimization of Guess Transition State using 6-31G(d) Basis Set

In order to make an comparison between different methods and avoid the error caused by previous calculation, the guess transition state is optimized using the more accurate 6-31G(d) basis set. The initial structure is exactly the same guess structure in previous session, i.e., interfragment distance is set to 2.2 Å.

1. Optimized Transition State

test molecule

2. Key Information of Result

Method	Optimization to TS(Berny)
Basis Set	6-31G(d)
Key Word	Opt=NoEigen
Total Energy	-234.54389655 a.u.
Number of Imaginary Frequency	1
Wavenumber of Imaginary Frequency	-525.04 cm-1

3. Validity of Result

3.1 Real Output

        Item               Value     Threshold  Converged?
Maximum Force            0.000008     0.000450     YES
RMS     Force            0.000001     0.000300     YES
Maximum Displacement     0.000219     0.001800     YES
RMS     Displacement     0.000056     0.001200     YES
Predicted change in Energy=-8.090440D-10
Optimization completed.
   -- Stationary point found.

All parameters converged to confirm there is an energy minimum.

3.2 Frequency Analysis

Only one imaginary frequency at -525.04 cm-1, indicating the existence of transition state. The vibration mode for this frequency is displayed as below.

However, there is a large difference in imaginary frequency between two methods. As discussed before, this is a result from the difference in level of accuracy. Since no literature value is found, it is difficult to judge which result is more accurate.

4. File Link

To access the .log file of optimization, click here; and click here for a screenshot of calculation summary.

Result and Discussion

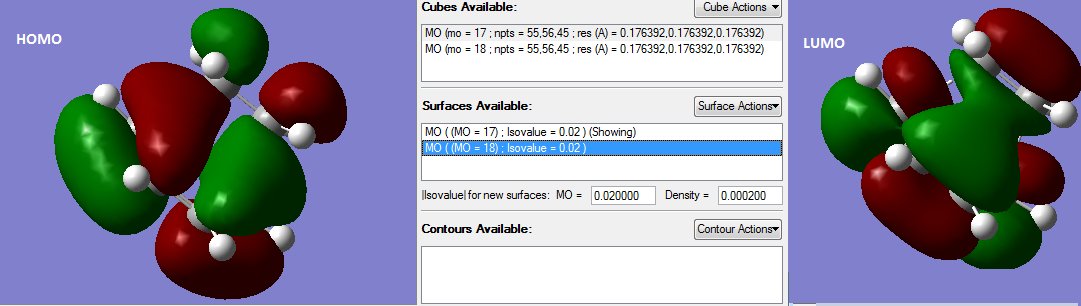
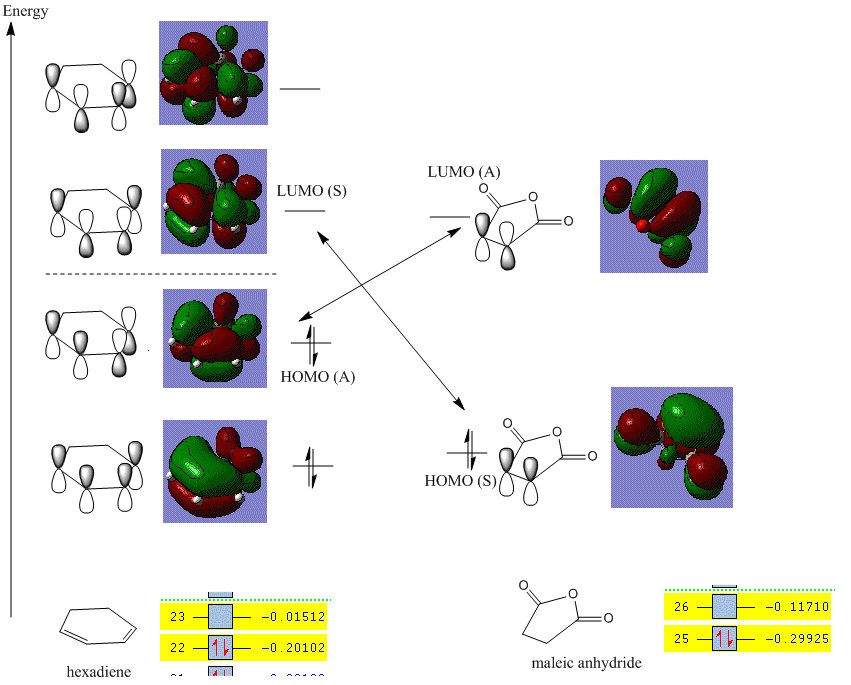
1. Molecular Orbitals

The molecular orbital for both reactants and product is drawn as following. The visualized molecular orbitals and relative energies are taken from the first optimization (using AM1 semi-empirical MO).

(Click here for an enlarged image.)

There are two requirements for a pericyclic reaction to happen:

1. interaction of HOMO and LUMO

2. interaction only happens between orbitals of same symmetry

According to the molecular orbital, this [4+2] cycloaddition is allowed because there are two possible interactions of the reactants:

1. HOMO of butadiene and LUMO of ethylene which are both anti-symmetric

2. LUMO of butadiene and HOMO of ethylene which are both symmetric

Furthermore, this reaction is classified as π4s + π2s cycloaddition, which proceeds via Hückel topology involving only suprafacial components (or via two antarafacial components, which is quite rare).

2. General Geometry Data

The optimized parameters of transition state are compared with literature as below.

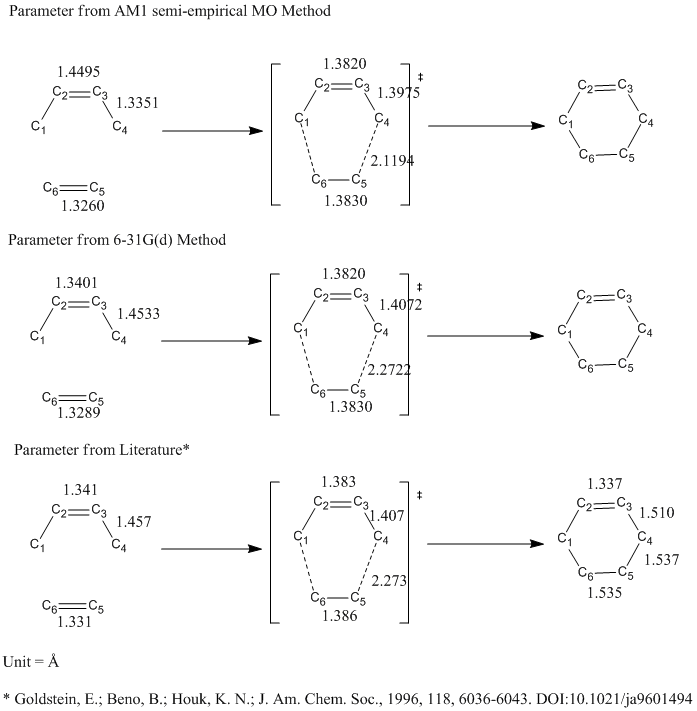
Parameter	Result from AM1 Optimization	Result from 6-31G(d) Optimization	Literature Value
C1-C2 and C3-C4 Bond Length/ Å	1.3820	1.3820	1.383
C2-C3 Bond Length/ Å	1.3975	1.4072	1.407
C5-C6 Bond Length/Å	1.3830	1.3830	1.386
C1-C6 and C4-C5 Interfragmental Distance/ Å	2.1194	2.2722	2.273

Apparently the 6-31G(d) method gives a much more accurate structure that have all parameters closer to literature than the AM1 semi-empirical MO method. The 6-31G(d) method makes nearly perfect agreement with literature while AM1 semi-empirical MO method only produces a similar structure. However, the 6-31G(6) tends to be much more time consuming and less effective if larger number of calculations are involved.

Comparison of the structural parameters of reactants is also achieved. An illustration of how close the optimized parameters are to literature is shown below.

Similarly, the 6-31G(d) method performs much better in determination of the transition state comparing to literature. The AM1 semi-empirical MO method only give prediction of a precise structure but it has been used more often due to the time efficiency.

Some typical carbon bond lengths are also found and tabulated as following:

Bond Type	Bond Length/ Å
C(sp3)-C(sp3) Bond	1.330
C(sp2)=C(sp2) Bond	1.470
C(sp3)-C(sp2) Bond	1.50*

• In this paper, the C=C bond length is suggested to be 1.54 Å and C-C bond length suggested to be 1.35 Å. This proves that C(sp³)-C(sp²) bond length lies between C(sp²)=C(sp²) bond and C(sp³)-C(sp³) bond. It could be misleading if only comparing relative values found in different papers.

In the transition state, the sp² C=C bond is generally shorter than typical value and sp³ C-C bond is slightly longer than typical value. This gives indication that they are neither pure C=C double bond or pure C-C single bond, but a state between.

3. Reaction Mechanism

According to the animation of the transition state, two sigma bonds are formed synchronously. This can be compared with the vibration mode of lowest positive frequency shown as following.

The HOMO and LUMO of modified transition state from AM1 semi-empirical MO is shown below:

It is clear that HOMO is anti-symmetric(A). It shows a weak bonding character formed by interaction between ethylene LUMO and butadiene HOMO and has energy of -0.32395 a.u.

In contrast, the LUMO is symmetric(S). It has anti-bonding character and formed by interaction between ethylene HOMO and butadiene LUMO. The energy of orbital is 0.02317 a.u.

The interaction between orbitals is shown below.

As discussed in the molecular orbital session, there are technically two possible interactions in transition state (HOMO could be either A or S). The reason why only one is presented is that in this case, the HOMO of butadiene is more electron sufficient than HOMO of ethylene. Therefore, it fills up the electron deficient LUMO of ethylene more effectively and provides extra stabilization towards the system.

4. Yield of Reaction

It is noticed that, normally the yield of this certain Diels Alder reaction is suggested to be quite low comparing to others. The major reason is that the reactant, cis-butadiene is an unfavoured structure comparing to trans-butadiene.

The reason accounting for this phenomenon is simply steric hindrance. In order to improve the yield, other reaction routes can be taken such as adding electron withdrawing groups to alkene to increase conjugation.

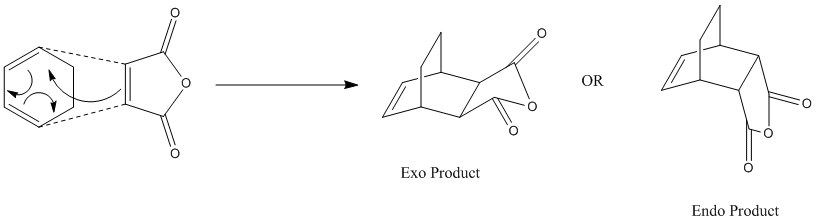
Reaction Between Cyclohexa-1,3-diene and Maleic Anhydride

Another Diels Alder reaction between cyclohexa-1,3-diene and maleic anhydride will be investigated in this session, in order to obtain more detailed information of the regioselectivity during reaction. Due to the addition of electron withdrawing groups on the alkene, extra stability is provided towards the molecular orbitals, thus improves yield. In reality, this type of reaction is firstly developed between maleic anhydride and cyclopentadiene. This becomes quite popular but technically demanding because of the unavoidable self-cycloaddition of cyclopentadiene. Though the problem will be neglected in computational labs, the reactant is still chosen to be cyclohexa-1,3-diene rather than cyclopentadiene. The calculation involving in the addition of an extra carbon atom will not be too costy in this experiment.

The reaction scheme is drawn as following.

There are two possible products, one is thermodynamic and the other one is kinetic. In this experiment, more detailed analysis and investigation between these two adducts will be made.

Optimization of Reactants

Similarly, the transition states could be modified based on optimized reactants. In this session, the two reactants will be optimized using high accurate methods.

Optimization of Maleic Anhydride

1. Optimized Maleic Anhydride Molecule

test molecule

2. Key Information of Result

Method	Optimization to a minimum
Basis Set	B3LYP/6-31G(d)
Total Energy	-379.28954412 a.u.
Current Symmetry Group	C2v

3. Validity of Result

        Item               Value     Threshold  Converged?
Maximum Force            0.000292     0.000450     YES
RMS     Force            0.000094     0.000300     YES
Maximum Displacement     0.001338     0.001800     YES
RMS     Displacement     0.000551     0.001200     YES
Predicted change in Energy=-4.590503D-07
Optimization completed.
   -- Stationary point found.

Real output shows all parameter converged, therefore it is optimized to an energy minimum.

4. File Link

To access the .log file of optimization, click here; for a screenshot of calculation summary, click here.

Optimization of Cyclohexa-1,3-diene

1. Optimized Cyclohexa-1,3-diene Molecule

test molecule

2. Key Information of Result

Method	Optimization to a minimum
Basis Set	B3LYP/6-31G(d)
Total Energy	-233.41588484 a.u.
Current Symmetry Group	C2v

3. Validity of Result

        Item               Value     Threshold  Converged?
Maximum Force            0.000275     0.000450     YES
RMS     Force            0.000038     0.000300     YES
Maximum Displacement     0.000532     0.001800     YES
RMS     Displacement     0.000141     0.001200     YES
Predicted change in Energy=-1.439597D-07
Optimization completed.
   -- Stationary point found.

Real output shows all parameter converged, therefore it is optimized to an energy minimum.

4. File Link

To access the .log file of optimization, click here; for a screenshot of calculation summary, click here.

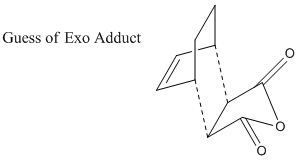
Optimization of Exo Product

As did in previous sessions, the transition states are guessed and optimization is based on the predicted structure. The guessed exo structure is shown as following.

1. Optimized Exo Adduct

test molecule

2. Key Information of Result

Method	Optimization to TS(Berny) + Frequency
Basis Set	AM1 semi-empirical MO
Key Word	opt=noeigen
Total Energy	-0.05041985 a.u.
Number of Imaginary Frequencies	1
Wavenumber of imaginary Frequency	-812.21 cm-1

3. Vibration Modes

3.1 Vibration Mode of Imaginary Frequency

Imaginary frequency at -812.21 cm^-1.

3.2 Vibration Mode of First Positive Frequency

Real frequency at 60.85 cm^-1

4. Validity of Result

4.1 Real Output

        Item               Value     Threshold  Converged?
Maximum Force            0.000002     0.000450     YES
RMS     Force            0.000000     0.000300     YES
Maximum Displacement     0.000023     0.001800     YES
RMS     Displacement     0.000004     0.001200     YES
Predicted change in Energy=-9.272514D-12
Optimization completed.
   -- Stationary point found.

The the parameters converged to give an energy minimum.

4.2 Frequency Analysis

There is only one imaginary frenquency, confirming that there is a transition state.

5. File Link

To access the file link to .log file of optimization, click here; for a screenshot of calculation summary, click here.

Optimization of Endo Product

The guessed endo structure is shown as following.

1. Optimized Endo Adduct

test molecule

2. Key Information of Result

Method	Optimization to TS(Berny) + Frequency
Basis Set	AM1 semi-empirical MO
Key Word	opt=noeigen
Total Energy	-0.05150478 a.u.
Number of Imaginary Frequencies	1
Wavenumber of imaginary Frequency	-806.47 cm-1

3. Vibration Modes

3.1 Vibration Mode of Imaginary Frequency

Imaginary frequency at -806.47 cm^-1

3.2 Vibration Mode of First Positive Frequency

Real frequency at 62.51 cm^-1

4. Validity of Result

4.1 Real Output

        Item               Value     Threshold  Converged?
Maximum Force            0.000021     0.000450     YES
RMS     Force            0.000003     0.000300     YES
Maximum Displacement     0.001021     0.001800     YES
RMS     Displacement     0.000145     0.001200     YES
Predicted change in Energy=-2.286561D-08
Optimization completed.
   -- Stationary point found.

All parameters converged to a small number to give an energy minimum.

4.2 Frequency Analysis

There is only one imaginary frenquency, confirming that there is a transition state.

5. File Link

To access the .log file of optimization, click here; for a screenshot of the calculation summary, click here.

Result and Discussion

1. Molecular Orbitals

Similarly, the reaction path can be discussion in the viewpoint of molecular orbitals. A sketch of how the components are interacted is displayed as following.

Very similar to the Diels Alder reaction between butadiene and ethylene, technically it seems to be two possible overlaps:

1. interaction between HOMO of hexadiene and LUMO of alkene, which are both anti-symmetric(A)

2. interaction between LUMO of hexadiene and HOMO of alkene, which are both symmetric(S)

Normally, the allowed mechanism is via case 1 where HOMO of diene appears to be more electron sufficient to fulfill the electron deficiency of LUMO of alkene. The pi electron overlap in diene also provides extra stabilization towards the system. However, in this reaction, the allowed mechanism is via case 2. The reason is that the attached electron withdrawing groups on alkene stabilizes the system and brings HOMO down in energy as the above diagram shows.

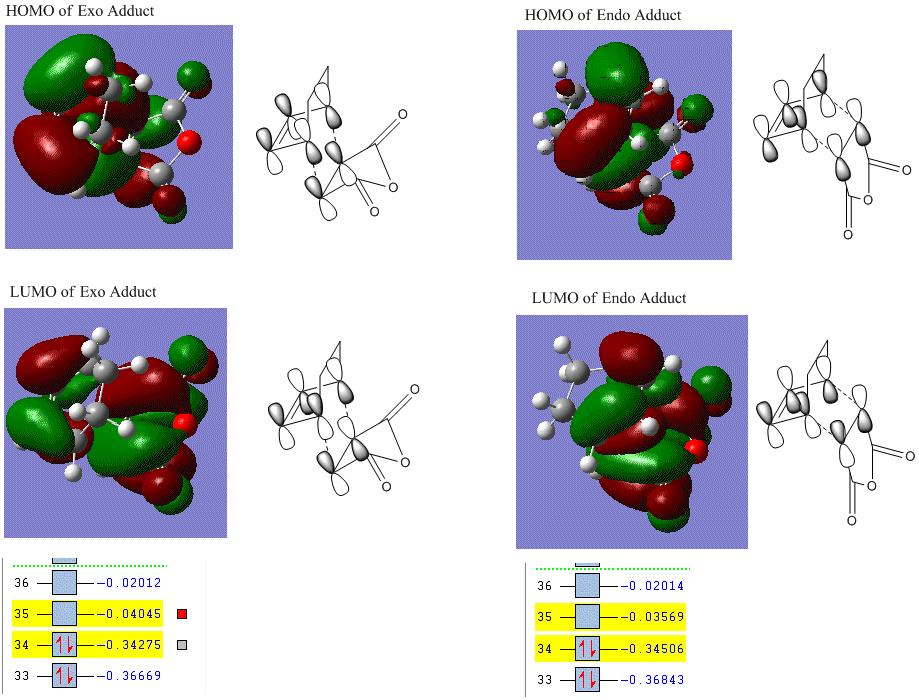
The HOMO of LUMOs of exo and endo adducts are displayed and compared as well.

These visualized orbitals make confirmation on the previous prediction that the HOMO of transition state is a result from the interaction between HOMO of maleic anhydride and LUMO of cyclohexadiene. LUMO of the transition state is in therefore fomr the interaction between LUMO of maleic anhydride and HOMO of cyclohexadiene.

HOMOs are anti-symmetric and LUMOs are symmetric.

The energy gap between exo adduct HOMO-LUMO is 0.30230 a.u., which is 189.70 kcal/mol.

The energy gap between endo adduct HOMO-LUMO is 0.30937 a.u., which is 194.13 kcal/mol.

The HOMO-LUMO gap of each adduct does not differ much in energy. HOMO of exo adduct lies slightly lower in energy than endo adduct but the relative energy of LUMO is opposite, i.e., LUMO of endo adduct lies lower in energy than exo product.

2. Relative Energy

The total energy of exo adduct = -0.05041985 a.u.

The total energy of endo adduct = -0.05150478 a.u.

Relative energy = 0.00108493, which equals 0.68080 kcal/mol.

Comparing to the energy difference between HOMO and LUMO, the relative energy between two adducts are not large in magnitude. This indicates that reaction mechanism via both transition states are possible because energy barrier is not too high to overcome.

From the scheme above, he endo adduct seems to be more strically hindered than the exo adduct and thermodynamically less stable. However, experiment shows that the endo adduct is the predominant product. The main reason is due to second orbital overlap, which is caused by the electron withdrawing groups attached at alkene(in this case, C=O groups). The interaction of pi orbitals on C=O groups with HOMO of diene(general case, in this specific reaction, LUMO of diene)in endo transition state provides extra stability towards system, thus makes endo adduct lower in energy.

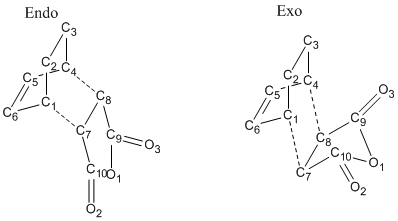
3. General Geometry Data

The parameters from each optimized transition state are tabulated and compared as following as well as the numbering of atoms.

Parameter	Optimized Exo Transition State	Optimized Endo Transition State
C1-C7 and C4-C8 Interfragmental Distance/ Å	2.1704	2.1623
C5=C6 Bond Length/Å	1.3968	1.3972
C7-C8 Bond Length/ Å	1.4101	1.4085
C1-C6 and C4-C5 Bond Length/ Å	1.3944	1.3930
C7-C10 and C8-C9 Bond Length/ Å	1.4882	1.4892

The overall geometry of each fragment (diene or alkene) does not experience a vigorous change from exo transition state to endo transition state as the bond lengths and bond angles stays almost unchanged. Comparing to the typical carbon-carbon bond lengths (there is tabulation in previous session), it is clear that neither pure double bond character nor pure single bond character is very obvious. Instead, the partial bond between double and single bond lengths occurs in the transition state. The interfragmental distance is quite close to the guess structure which is 2.1 Å.

The calculated bond lengths are not compared with literature because the AM1 semi-empirical MO method is not accurate enough in determination of structure. They might differ too much from literature and therefore does not make any sense. A more accurate method such as using 6-31G(d) basis set could be carried out if time allows to make more accurate determination in terms of structure.

4. Activation Energy and Yield

The reaction is assumed to be under kinetic control, with low temperature and short reaction time.

In this reaction, endo adduct is the major product, which has mechanism via the transition state with energy barrier that is easier to overcome. Exo adduct is the thermodynamic product which requires high temperature and long reaction time.

Activation Energy of this reaction can be calculated if the optimization of transition states are using the same basis set as the optimization of reactants(6-31G* in this case).

In this particular reaction, yield can be improved by addition of e.g. Lewis acid, which also alters the relative ratio of exo and endo products. For general Diels Alder reactions, other method including using chiral reagents or chiral catalysts can also be applied in order to control the ratio of either adduct.

Further Discussion

There are many other factors that have influences on the transition states. Further investigation into these factors will provide more specific aspects on the property of transition states in Diels Alder reactions. Due to time limitation, these calculations cannot be carried out to give real results. Only theoretical prediction will be made in a general manner.

1. Reaction Condition: By rising temperature of extend reaction time, the equilibrium will move towards the thermodynamic product.

2. Solvent: during the optimization, all the solvent have been set as 'none'. Here is an example by Alexander Wittkopp discussing on the solvent effect of reaction kinetics of the following Diels Alder reaction.

Computational interpretations of the solvent effect can be achieved using Gaussian as well. There are also many evidences showing that the rate of reaction is effected greatly by solvent.

3. Catalyst: the major role of catalyst is to reduce the activation energy barrier of reaction. Therefore, reaction rate will be increased. If some specific type of catalyst which only lowers activation energy of one transition state is applied, the ratio of resultant adducts will be altered as well.