Rep:Js5515transitionstates

Introduction

Potential Energy Surfaces (PES)

As can be seen in this lab, a reaction may proceed via a number of different transition states. The transition state on a PES is a point at which energy decreases in one direction but increases in all others, it corresponds to the maximum on the minimum energy pathway whereas a minimum is a point from which energy increases in all directions.

The first derivative of a point on a PES can be used to see if the point is a minimum or a TS. A minimum is described as a point where the first differential is 0 and the second differential is positive. A 'real' minima corresponds to the configuration of a molecule that has the lowest energy. There are different types of minima, namely local and global. A local minima (there may be several on a PES) corresponds to multiple similar configurations and a global minima (there is only one on a PES) corresponds to the lowest energy of all possible configurations. To see if we have reached a global minimum in GaussView, we can check the frequencies of the vibrational modes of the molecule. When all the vibrations are of positive frequencies, we have reached the global minimum of the PES. When one vibration frequency is negative, we have reached a TS. The positive frequencies are due to the positive force constants associated with the increase in energy in all directions from a local minima, whereas the one negative frequency corresponds to the negative force constant associated with the reaction pathway in a TS.

Nf710 (talk) 22:21, 22 February 2018 (UTC) You have shown some understanding but this is quite brief. You need to mention how you on are a PES of 3N-6 coords and that you can get the eiegenvalues of the hessian matrix to be the force constants and the eigenvectors to be the vinrational modes

Calculation methods used in the lab

For this lab we mainly use the semi-empirical PM6 and B3LYP levels. The PM6 method is based on the Hartree-Fock model, it uses empirical data and approximations in calculations in order to reduce the power needed to process and solve the Hamiltonian. This makes this method the most inexpensive and was the main method used throughout this lab. There are however downsides to using so many approximations - results can be inaccurate and may not truly reflect the PES of a reaction.

B3LYP (used in exercise 2) uses density functional theory to solve the Hamiltonian. Unlike the semi-empirical PM6 level, B3LYP only approximates the exchange correlation term, all the other terms are calculated exactly. Computing many more terms of the Hamiltonian exactly requires much more processing power and is therefore more time intensive.

Nf710 (talk) 22:24, 22 February 2018 (UTC) Good understanding of PM6, B3LYP does not approximate the XC term. that is just an artiffact of DFT. it uses a HF calculation to calculate that term hence why it is know as a hybrid term.

Exercise 1: Reaction of Butadiene with Ethene

(Fv611 (talk) Great job across the whole exercise! Very well done :) )

Reaction Scheme

MO Analysis

MO Diagram

Reactant and Transition State Orbitals

Figure 3: The HOMO and LUMO of the reactants, butadiene and ethene

HOMO

LUMO

Butadiene

Ethene

Figure 4: HOMO-1, HOMO, LUMO + LUMO+1 of the TS for the reaction between butadiene and ethene

HOMO-1

HOMO

LUMO

LUMO+1

Transition State

MO Comments

Figure 2 shows an MO diagram for the reaction between butadiene and ethane and Figures 3 and 4 are a visualisation of the reactant and transition state MOs. Figure 1 shows the HOMO(S) of the butadiene interacting with the LUMO(S) of the ethene to give two symmetrical orbitals in the transition state whilst the HOMO(AS) of the ethene interacts with the LUMO(AS) of the butadiene to give two AS MOs in the transition state. From this MO diagram it can easily be seen that there is no interaction between orbitals of differing symmetries and only orbitals of like-symmetry have interacted to form new MOs in the transition state. A constructive interaction between two MOs requires the overlap integral to be non-zero and this is only satisfied when two orbitals of the same symmetry interact. Further to the symmetry requirement, for an interaction to be 'allowed', the orbitals must be of similar energies and interact to reduce the overall energy of the system. If these requirements are not met, an interaction will be 'disallowed'.

The strongest interaction for this reaction takes place between the HOMO of the butadiene (diene) and the LUMO of the ethene (alkene), these orbitals are both antisymmetric and are the closest in energy of any orbitals sharing the same symmetry. It is for this reason that their interaction is the strongest and leads to the formation of two new MOs with a larger splitting than those formed between the symmetric MOs. If two orbitals of differing symmetry overlap the integral between them will be equal to zero as any constructive overlap between lobes is cancelled out by equal and opposite destructive interaction by other lobes.

In this reaction, we have a relatively electron rich diene and an electron poor dienophile meaning the reaction is a normal electron demand Diels-Alder reaction. The MO diagram shows that the electrons involved in the formation of the TS have gained energy resulting in a TS that is higher in energy than the reactants - this difference in energy is the energy barrier that must be overcome for a reaction to proceed.

Bond Lengths

Typical Bond Lengths
sp²-sp² 1.34 Å
sp³-sp³ 1.54 Å

Figure 5 shows the bond lengths of the reactants, transition state and product. As can be seen, the bond lengths change throughout the course of the reaction. The C-C bond in butadiene shortens during the reaction as a C=C bond is being formed in the transition state. The bond length observed between these two carbons in the transition state is between the single C-C and double C=C bond lengths observed in the reactants and products respectively.

The reaction between these two molecules involves the breaking of three C=C bonds to leave C-C sigma bonds. It would therefore be expected that the bond length between these carbons would increase, this is clearly the case with the bond lengths in the TS lengthening and ending in the products at ~the typical length of a C-C sigma bond.

The two sigma bonds that form between the butadiene molecule and the ethene molecule are much longer than the average C-C sigma bond in the transition state. The distance between the the carbons is within twice the Van Der Waals Radius and therefore it can inferred that the orbitals are interacting in the process of bond formation.

The bond lengths in the TS are closer to the lengths in the reactants which suggests this is an early stage TS, this can be confirmed by looking at the IRC of the reaction which shows the TS energy is much closer to that of the reactants than the products.

Transition State Vibration

Figure 6: Transition state vibration showing the changing lengths of the bonds during the reaction

The imaginary frequency of vibration for this reaction is -948.75 cm^-1 and the negative force constant causes the negative frequency of the vibration. Figure 6 shows the vibrations in the transition state and from this it can be seen that the formation of the two bonds is synchronous as both the ethene and butadiene carbons approach each other at the same time.

Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

Reaction Scheme

MO Analysis

MO Diagram

(Fv611 (talk) Your diagrams are well made, but you should have discussed the differences between the endo and exo conformations in terms of the relative energies of the MOs)

**Figure 9:** MO Diagram for the Endo Product Formation

Reactants

Figure 10: Visualisation of the HOMO and LUMO of the reactants, Cyclohexadiene and 1,3-Dioxole

HOMO

LUMO

Cyclohexadiene

1,3-dioxole

Transition State

Figure 11: Visualisation of the HOMO-1, HOMO, LUMO + LUMO+1 of the Exo and Endo Transition States for the reaction of Cyclohexadiene with 1,3-Dioxole

HOMO (-1)

HOMO

LUMO

LUMO (+1)

Endo Transition State

Exo Transition State

Reaction Comments

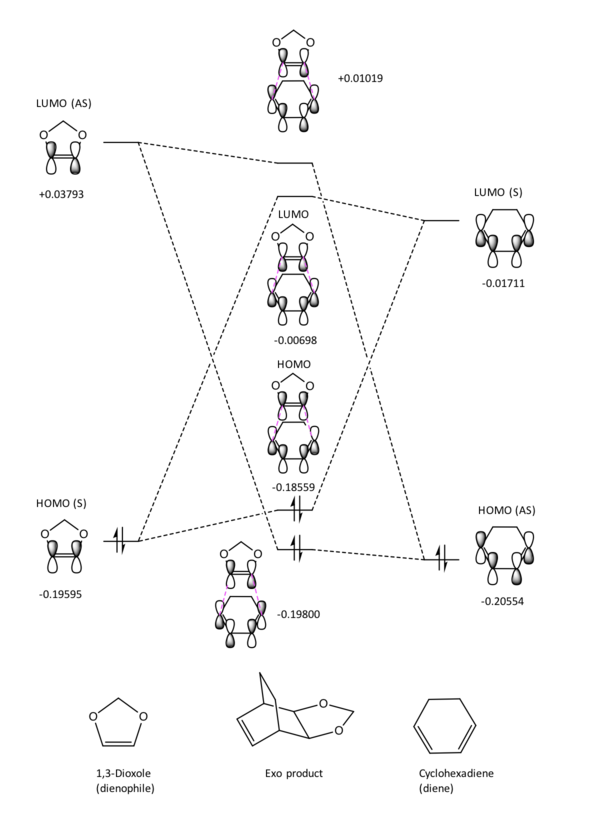
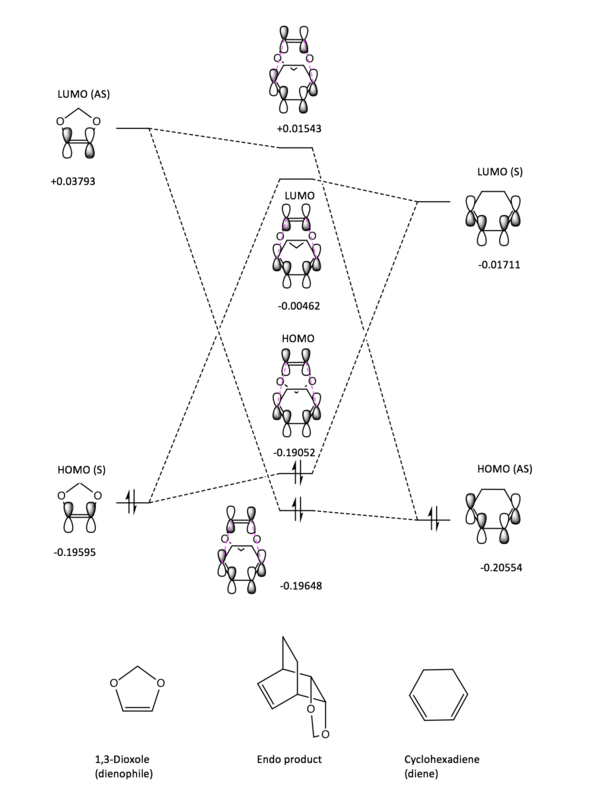
As in exercise 1, only orbitals of the same symmetry and of similar energy can interact to form new MOs and lower the overall energy of the system. However, in this reaction the relative energies of the TS for the exo and endo reactions are different. In the endo reaction, the lone pairs of the oxygens interact with the pi system of the cyclohexadiene, this interaction lowers the energy of the HOMO in the transition state and in turn lower the overall energy of the TS system relative to the energy of the TS in the exo reaction.

Figures 8 and 9 show that in this reaction, it is the HOMO of the dienophile interacting with the LUMO of the diene to form the TS. By running an energy calculation of the last point of the IRC for this reaction, both reactants were on the same potential energy surface and their energies could be compared relative to one another as they have the same Hamiltonian potentials. This calculation allowed us to confirm that this reaction proceeds via an inverse electron demand Diels-Alder where the strongest frontier molecular orbital interaction is between the HOMO of the dienophile and the LUMO of the diene. This relative energy difference can be attributed to either electron withdrawing groups on the diene lowering the energy of its HOMO or electron donating groups on a dienophile raising the energy of the HOMO. In this reaction it is the latter, the electron-donating oxygen pair on the 1,3-Dioxole (dienophile) donate electron density into the C=C bond of the alkene. This raises the energy of the pi and pi^* orbitals and thus raises the energy of the HOMO on the dienophile relative to the HOMO of the diene and makes this reaction an inverse electron demand Diels-Alder.

Nf710 (talk) 22:32, 22 February 2018 (UTC) You have just stated this with out any proof of you actually doing it. you havent given any figure either. Your reasoning is correct you just have nothing to back it up.

Reaction Calculations

Opt+freq calculations were carried out on the reactants, TS and product for both the exo and endo reaction pathways at the B3LYP level. The energies are shown in Table 1 below.

**Table 1:** Collected energy data for the exo and endo reaction pathways between Cyclohexadiene and 1,3-Dioxole
	Reactants (kJ/mol)	Transition State (kJ/mol)	Product (kJ/mol)	Activation Energy (kJ/mol)	Reaction Energy (kJ/mol)
Endo	-1313782	-1313622	-1313849	160	-67
Exo	-1313782	-1313614	-1313846	168	-64

Nf710 (talk) 22:37, 22 February 2018 (UTC) This is not enough precision.

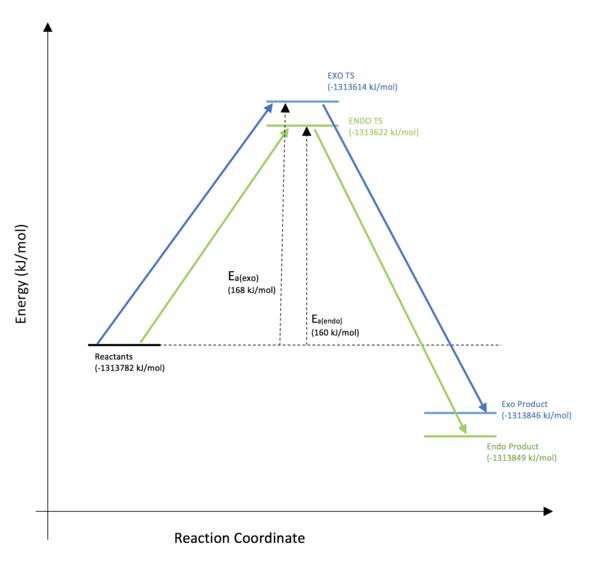
**Figure 12:** A reaction energy profile diagram for the exo and endo reactions

This data (visually represented in Figure 12, shows that the endo reaction pathway yields both the thermodynamic and the kinetic product. The smaller activation energy is due to the previously discussed lowering of the TS state energy due to favourable interactions between the oxygen lone pairs and the alkene C=C. This stabilisation is not seen in the exo transition state as the geometry does not allow the p-orbitals on the oxygens to donate into the alkene.

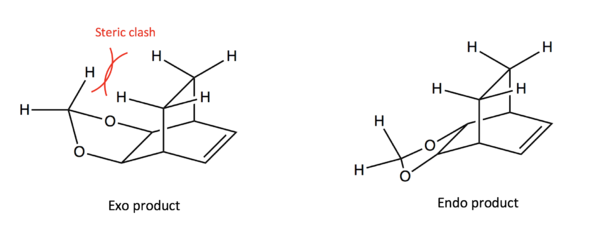
**Figure 13:** Schematic to show steric clash between hydrogens in the the exo product

It would typically be expected that the exo product is the thermodynamically more stable product in Diels-Alder reactions. In this reaction however, there is steric clash between the hydrogens of the Cyclohexadiene ring and the hydrogens of the 1,3-Dioxole group, as can be seen in Figure 13. This raises the energy of the product and renders the endo product both the kinetic and thermodynamic product.

Nf710 (talk) 22:38, 22 February 2018 (UTC) This was an o sectio, your discussion was very brief and not detailed enough in some parts. You did however get the correct results and you have complemented your discussion with some nice diagrams

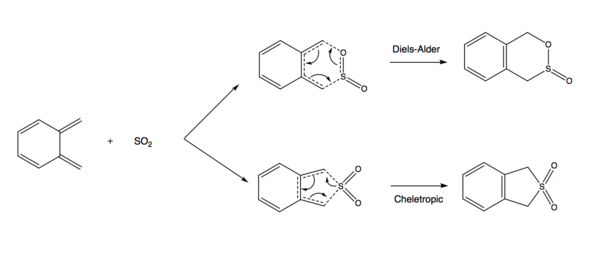
Exercise 3: Diels-Alder vs Cheletropic

Reaction Scheme

IRC Calculations

**Figure 15:** GIFs showing the possible reaction pathways and the IRC energies
Reaction Type	IRC	Energy along the IRC
Exo-Diels-Alder
Endo-Diels-Alder
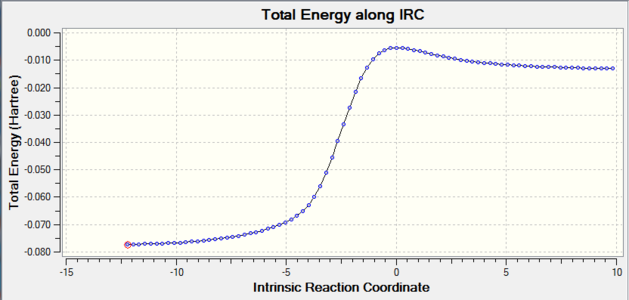
Cheletropic

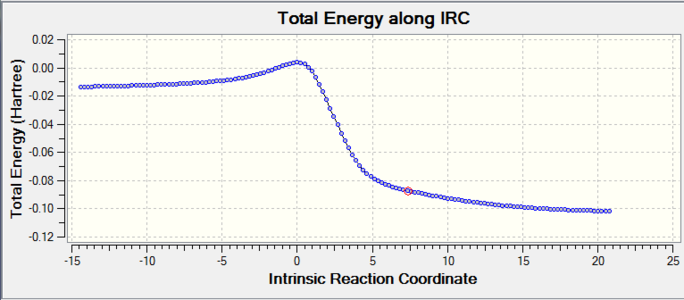
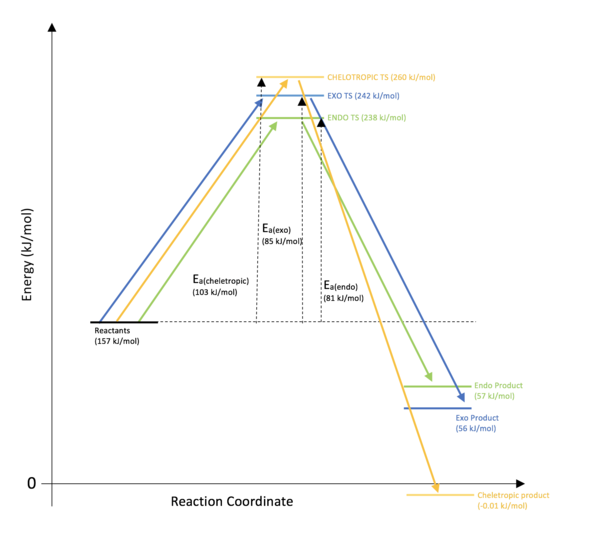
Reaction Calculations

**Table 2:** Collected energy data for the exo and endo and cheletropic reaction pathways
	Reactants (kJ/mol)	Transition State (kJ/mol)	Product (kJ/mol)	Activation Energy (kJ/mol)	Reaction Energy (kJ/mol)
Endo	157	238	57	81	-100
Exo	157	242	56	85	-101
Cheletropic	157	260	-0.01	103	-157.01

The data in the above table is visualised in Figure 16. Similarly to exercise 2, the endo TS state has the lowest energy due to stabilising interactions of the oxygen p-orbitals on the sulphur dioxide with the C=C of the alkene. The endo product is therefore the kinetic product and will be produced the most quickly.

(You've missed out reaction energies. See here for comments Tam10 (talk) 11:13, 27 February 2018 (UTC))

Although the formation of the cheletropic product has the highest activation energy, the product formed is the most stable/thermodynamic product. All of the products contain an energetically stable 6-membered aromatic ring, but both the exo and endo products contain another non-aromatic 6-membered ring. These rings do however contain a sulphur atom which is much larger than carbon and therefore distorts the geometry and puts strain on the non-aromatic ring. The cheletropic product contains two strong S=O bonds (compared to the one in the exo and endo products) - this coupled with a potentially more sterically stable 5-membered ring leads to the cheletropic product being the more energetically stable of the three, making it the thermodynamic product.

Alternative Reaction Pathways

The o-Xylylene contains another diene (cis-butadiene fragment) that the SO₂ may react with. The thermochemical data for these side reactions is shown in Table 3. This data shows that the activation energies are much higher than for the reactions with the terminal cis-butadiene. One reason why the TS energies are lowered for the reactions with the exocyclic diene is that the TS gains a degree of aromaticity, lowering the energy of both the TS and the products.

It can also be noted that both of these alternative pathways have positive reaction energies, meaning the reactions are endothermic and are therefore not favoured thermodynamically. These reactions are unlikely to take place as they are out-competed both kinetically and thermodynamically.

**Figure 17:** GIFs and IRC data for the alternative endo and exo reaction pathways
Reaction Type	IRC	Energy along the IRC
Alternative Exo-Diels-Alder
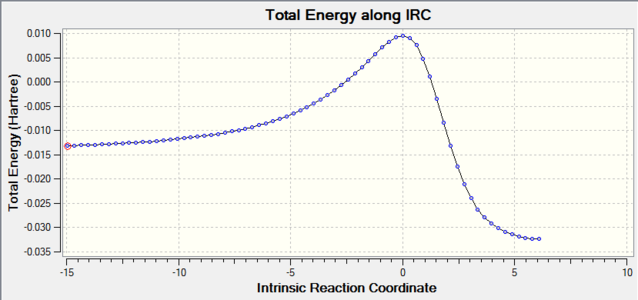
Alternative Endo-Diels-Alder

**Table 3:** Collected energy data for the alternative exo and endo reaction pathways between SO₂ and o-Xylylene
	Reactants (kJ/mol)	Transition State (kJ/mol)	Product (kJ/mol)	Activation Energy (kJ/mol)	Reaction Energy (kJ/mol)
Endo	157	268	172	111	+15
Exo	157	276	177	119	+20

Supporting Files

The IRC Files are attached below
Exo: File:JS5515EXOIRC.LOG
Endo: File:Js5515ENDOIRC.LOG
Cheletropic: File:Js5515CHELETROPICIRC.LOG
Alternative Exo: File:JS5515ALTEXOIRC.LOG
Alternative Endo: File:JS5515ALTENDOIRC.LOG

Further Works

Reaction Scheme

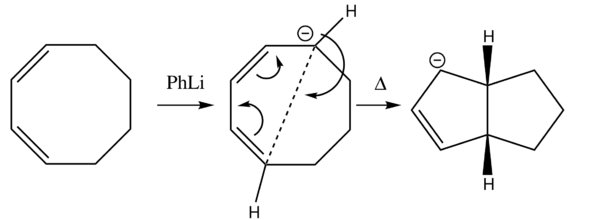
This electrocyclic reaction looks at the ring closure of 1,3-cycloctadiene using PhLi, only one of the alkene bonds is preserved in the product which contains two 5-membered rings.

To optimise this reaction, the semi-empirical PM6 level was used with method 2. The 1,3-cycloctadiene was drawn first and optimised to a ground state, a hydrogen was then removed and a Lithium ion places within the vicinity of the carbon with a negative charge. As per method two, the two carbons that were to be involved in the ring closure were frozen at 2.2 Å, a ground state and then TS optimisation were taken and then an IRC run on the resulting TS. The IRC animation in Figure 18 below allows us to see how the lithium ion essentially follows the negative charge, this is due to hard-hard interactions. Lithium is an extremely small hard positive ion and therefore has a great affinity for localised charges, rather than say a delta -ve charge.

**Figure 19:** IRC Animation showing the electrocyclic ring closure to form a bicyclic product

Reaction Calculations

As can be seen in Table 4, this reaction is exothermic. The two five-membered rings formed in the product are lower in energy than the starting octadiene ring. From our knowledge of favoured angles - this makes sense. An octadiene ring is strained, with interior angles far greater than those preferred by sp³ orbitals. Five membered rings however are much happier, their internal angles are around 108^o, very similar to the angles preferred by sp³ orbitals. This would suggest that the driving force for the ring closure is the release of steric strain to form the less energetic five membered rings.

**Table 4:** Collected energy data for the exo and endo reaction pathways between Cyclohexadiene and 1,3-Dioxole
Reactants (kJ/mol)	Transition State (kJ/mol)	Product (kJ/mol)	Activation Energy (kJ/mol)	Reaction Energy (kJ/mol)
433	615	415	182	-18

Concluding Remarks

In the three exercises in this lab, GaussView was used successfully to optimise three Diels-Alder reactions and one ring closure. The TS were found using both PM6 and B3LYP levels with the latter of which being a much more time intensive method due to the higher level of precision (far fewer approximations used in solving the Hamiltonian). Due to this, most of the calculations done in this lab were at the PM6 level, whilst not as accurate as B3LYP, the results obtained could be rationalised with knowledge of FMO's and steric interactions. By running calculations with both reactants on the same PES, we were able to visualise the relative energies of the MOs and gain information about the type of electron demand involved in the reaction - i.e. Inverse-electron demand Diels-Alder in Exercise 2. GaussView as a program allows us to carry out calculations and gain much information about bond lengths, TS, reaction pathways and activation energies. It also allowed us to produce accurate MO diagrams which further confirmed previous learnings on the symmetry and energy requirements of orbital interactions. From these MO diagrams it is easy to see that only orbitals of the same symmetry can interact constructively as they will have a non-zero overlap integral. Further to this, we can also see that orbitals must be of similar energies in order to interact and lower the overall energy of the TS.

Carrying out energy calculations on the thermochemical data collected from the log files, we were able to distinguish between the kinetic and thermodynamic products. The results could be rationalised by looking at the sterics and stabilising secondary orbital interactions in some of the products.

As expected, the bond length information gained from the optimisations showed us that the TS bond lengths were between the typical lengths of the reactant bond length and product length. This information allowed us to visualise if a TS was early or late by inspecting if the bond lengths in the TS were closer to those in the reactants (early TS) or those in the products (late TS).