Rep:Jir15comp2017

Introduction

Gaussian is a program that creates 3N-6 dimensional potential energy surfaces. Important energy points that are essential to determine the thermodynamic character of the molecules are obtained by analyzing the structure of the plot. The lowest energy conformations are obtained by determining the minima, which is done by calculating the first and second derivatives of the energy function. The transition states are located in the saddle points of the reaction, and always show a imaginary frequency due to the force constant (the second derivative) being 0 at that point. Two methods are used, PM6 and B3LYP/6-31G(d), the latter being more accurate due to taking into account parameters like the exchange conformation. In addition to Gaussian, the complementary program Gaussview allows us to view a physical representation of the molecules, their orbitals and the energy plots.

Nf710 (talk) 23:59, 16 November 2017 (UTC) This is not correct as the TS is at a saddle point and all the secondard deivatoves (of the 3N-6 ) are positive apart from the reaction coored which is at a maximum (along ths coord) hence its second derivative is negative.

Part 1: Diels-Alder reaction of butadiene and ethene diagram

Reaction overview and mechanism

The reaction is a typical example of the Diels-Alder process ([4+2] cycloaddition), that involves the formation of new bonds between a dienophile and a diene and a radical change in the bond structure of both reagents. The calculations were done by optimizing and calculating the frequencies via PM6.

(Fv611 (talk) You didn't specify what is in the log files that you appended at the end, so it is quite difficult to figure out if you have done the required optimisations.)

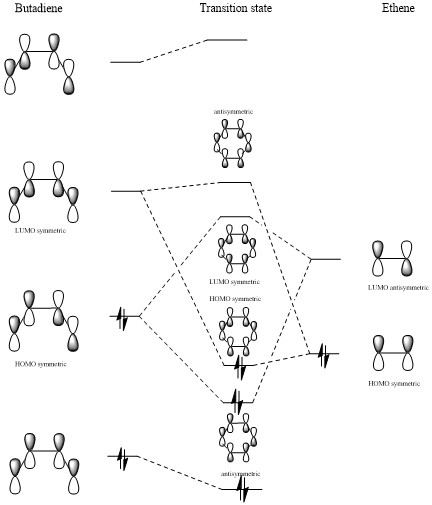
MO diagram

(Fv611 (talk) There are quite a few mistakes in this MO diagram. The HOMO of butadiene is antisymmetric, and reacts with the ethene LUMO to form two antisymmetric MOs. You also have drawn a symmetric HOMO as a combination of two antisymmetric FOs. The TS LUMO+1 is also wrong as it is drawn as a combination of a symmetric and an antisymmetric FO. These mistakes could have been avoided if you had thought more about the symmetry of your calculated MOs, and if you had related them to your diagram. Incidentally, you are lucky I realised that your MO tables have white titles and that you didn't miss out on all the labels.)

Orbital Analysis

As can be seen in the molecular orbitals diagram above, reactions are only allowed between fragment orbitals of the same symmetry sign. (Fv611 (talk) Unfortunately this cannot seen from your diagram.)

The overlap integral is non zero in case of symmetric-symmetric and antisymmetric-antisymmetric interactions, and zero in case of symmetric-antisymmetric interactions. The mathematical explanation lies in the fact that the integral of the product of an odd function and an even function, as the outcome is an odd function, while the opposite is true for the product of two odd functions or two even functions.

(Fv611 (talk) You could have pointed out that the symmetry requirements come from the value of the orbital overlap.)

Butadiene orbitals

Butadiene HOMO	Butadiene LUMO

Ethene MO's

Ethene HOMO	Ethene LUMO

MO images

TS HOMO-1	TS HOMO	TS LUMO	TS LUMO+1

Bond Analysis

The single bond C-C in butadiene has a length of 1.47070 Å, while the double bonds C=C are 1.33346 Å long. In ethene, the double bond C=C has a length of 1.32731 Å.

In the TS, the single bond C-C in butadiene has a length of 1.41106 Å, while the double bonds C=C are 1.37980 Å long. In ethene, the double bond C=C has a length of 1.38178 Å.

Cyclohexene molecule with atoms labelled

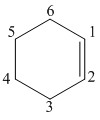
The lengths of the bonds of the products is listed in the following table:

Atoms	1-2	1-6, 2-3	3-4, 5-6	4-5
Distances (Å)	1.33784	1.50091	1.54040	1.54091

The increase in length of the double bonds in the butadiene to the equivalent single bonds in the product molecule is around 0.207 Å., while the single bond is shortened 0.133 Å as it becomes a double bond in the final product. The ethene double bond has a length increase of 0.214 Å. The smallest variation is in the formation of a double bond between 1 and 2 due to the equivalent single bond in butadiene being affected by the conjugation of the two adjacent alkene groups.

The Van der Waals radius of carbon is 1.7 Å, while the typical sp3 and sp2 C-C bond lengths are respectively 1.54 Å and 1.34 Å. The distance between the atoms forming the new bonds is 2.11 Å, well within the range of that radius.

(Fv611 (talk) Is it "well within that radius"? You said the radius is 1.7 and the forming bond is 2.11.)

The double bond is very close in lengthto the standard bond between sp2 carbons, as are all of the single bonds between sp3 carbons. The single bonds between the sp2 and the sp3 carbons are slightly shorter than the bonds between two sp3 carbons, but still closer to them than to the characteristic length of a sp3-sp2 bond.

Relevant files

File:DATSBE5.LOG File:DATSBE3.LOG

(Fv611 (talk) You are missing the illustration of the TS vibration, and the discussion about the synchronous/asynchronous bond formation in cyclohexene.)

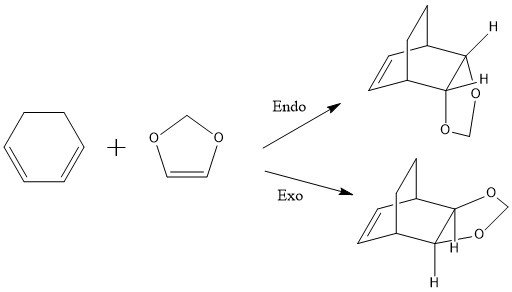
Part 2: Reaction of Cyclohexadiene and 1,3-Dioxole

Reaction overview and mechanism

The reaction is another type of of Diels-Alder, this time with two possible configurations in the products, endo and exo, that show differences in its kinetic and thermodynamic energies, and which originate in the position of the molecules relative to each other in the transition state. Again, the calculations needed involved obtaining the optimization and frequency of the reagents, both products and both transition states using first PM6 and then B3LYP/6-31G(d)

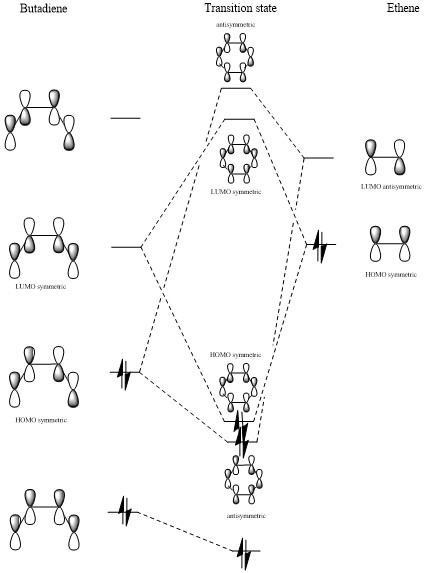
MO diagram

The orbitals of the dienophile are higher in energy than the previous case, due to them being more electron rich than the diene (thus making it an inverse demand reaction). Nonetheless, the orbital interactions are still the same, the main difference being the larger splitting in the interaction of the diene LUMO and dienophile HOMO due to the orbitals being closer in energy.

MOs of the endo TS

TS HOMO-1	TS HOMO	TS LUMO	TS LUMO+1

MOs of the exo TS

TS HOMO-1	TS HOMO	TS LUMO	TS LUMO+1

Thermodynamics

	Endo	Exo
Activation energy (kJ/mol)	101.425698	107.646
Activation energy (Hartrees)	0.038631	0.041
Reaction energy (kJ/mol)	-77.52314441	-73.92620913
Reaction energy (Hartrees)	-0.029527	-0.028157

Both reactions are exothermic in character. It can be seen from the values in the table that the favoured kinetic and thermodynamic product is the endo form (lower activation energy more negative reaction energy overall). The explanation lies in secondary orbital interactions, explained below.

Nf710 (talk) 00:01, 17 November 2017 (UTC) these should have been done at B3LYP as well as PM6 as it is a more computational expensive method and hence better.

Secondary orbital interactions

In the endo transition state, as well as having the diene-alkene interactions, the p-orbitals of the oxygens overlap with the p orbitals of two carbons in the diene, thus lowering the activation energy of the transition state and therefore stabilizing the molecule. This does not occur in the exo reaction, that only shows interactions of the first kind, as the two oxygen atoms are two far away to show any kind of activity. The calculations confirm these observation.

Nf710 (talk) 00:05, 17 November 2017 (UTC) Nice drawings and good understanding of the electron demand of the system. It is a shame you only did it at PM6 and also it would have been nice if you could have shown some understanding of the quantum mechanics behind the calculations.

Part 3: Diels-Alder vs Cheletropic

Reaction overview and mechanism

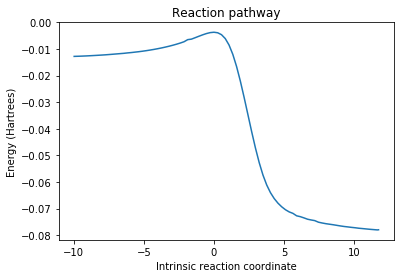
As in the previous case, the reaction shows two possible conformations, endo and exo, with different thermodynamic and kinetic properties. However, this time there is an extra possible third product that produces a symmetric molecule with cheletropic conformation. In order to obtain the thermodynamic properties, optimization and frequency calculations were performed with PM6, and an IRC was run to better observe the energy profile of the three possible reactions.

Thermodynamics

	Endo	Exo	Cheletropic
Activation energy (kJ/mol)	82.7583918	85.046403	105.08302
Activation energy (Hartrees)	0.031521	0.0323925	0.040024
Reaction energy (kJ/mol)	-98.03092647	-98.66892302	-155.009532
Reaction energy (Hartrees)	-0.037338	-0.037581	-0.05904
Reaction model
IRC

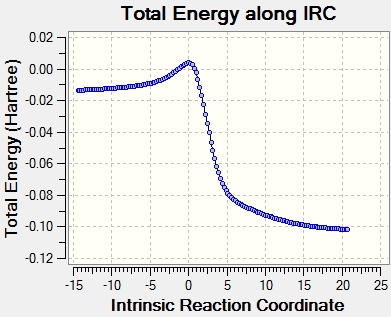
The three reactions are exothermic, but the cheletropic one is remarkable in having the largest activation energy and the most negative reaction energy, meaning that kinetically it will be the least favoured, but thermodinamically will be the most stable. Thus, it will be the preferred product when the reaction is carried out under high temperature. The thermodynamic data for the end and exo products is extremely similar, with the negligible differences between both conformations arising from secondary orbital effects in the endo onformation lowering the activation energy of the complex. All this information is shown in the diagram below; the reagents are assumed to be at infinite separation at the beginning.

Energy diagram

(A lot of decimal places. You need to think about how much you trust these numbers Tam10 (talk) 16:40, 10 November 2017 (UTC))

Bond analysis

One interesting feature of these reactions, which can be seen in the animated gifts, is that the cyclodiene becomes aromatic in the transition state by adopting a benzene like structure with conjugated bonds. The aromaticity helps to stabilize the molecule by lowering the energy.

Relevant files

File:SO2JIR15.LOG File:XYLILENE.LOG File:EXP3EXOIRC.LOG File:EXP3ENDOIRC.LOG File:CHELOTROPIC FINAL.LOG File:ENDOPRODUCTFINAL.LOG File:EXOPRODUCTFINAL.LOG File:EXP3CHELOFINALPRODUCT.LOG

Conclusion

The methods used by Gaussian proved to agree with the theory regarding the thermodynamic data of the different conformations (a perfect example would be the normally lower activation energy of the endo molecules in experiments 2 and 3 that arises from second orbital interactions). Other available tools like IRC allow a clear picture of the overall reaction path that is as well quite faithful to what happens in the laboratory. Nonetheless, the program still has issues, like its dependence on the manual design of the reagents for obtaining the different conformations, the frequent crashes and the long times involved in some of the calculations of the more complex molecules, that even sometimes fail to deliver a correct minimum energy in the optimization and the correct frequencies of the transition state.