Rep:JegaTS

Introduction

A non-linear molecule have 3N-6 internal degrees of freedom where N is the number of atoms in the molecule[1]. Varying two coordinates or the degrees of freedom in a system yields the potential energy surface. A minimum is the lowest energy point on the potential energy surface on a particular pathway or a region of the energy surface where reactants and products are found. Two types of minimum can be found on a potential energy surface, namely the local energy minimum and global energy minimum. More than one energy pathways are available for reactants to pass through in turning into the products and it is energetically favourable for the reaction to proceed through the lowest energy pathway. A reaction passing through this minimum energy pathway has to pass through an energy maximum on that pathway called the transition state. The transition state is the maximum point of a particular pathway but minimum of a different pathway which arises as a result of different degrees of freedom. The transition state is called a first-order saddle point.[2][3][4][5] This is illustrated in Figure 1.

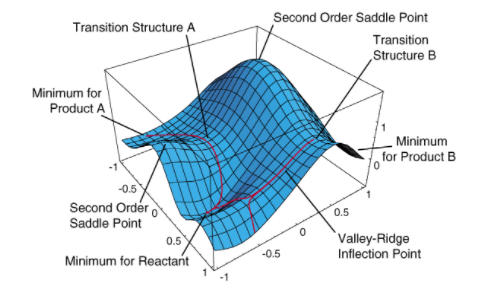
Figure 1: Potential Energy Surface (PES) showing minimum and transition state[6].

Both the minimum and transition state are referred to as stationary points and have a gradient of zero. The curvature(second derivative) is positive at a minimum and negative at a transition state. The movement of reactants and products on the minimum and the transition state can be related to Hooke's law(F=-kx) where F, k and x are restoring force, force constant and displacement respectively. Only upwards trajectory is possible from a minimum because it is at the lowest point of energy on the PES. On the other hand, only downwards movement is possible from the transition state on a reaction path as it is the energy maximum. The downwards movement from a transition state in a reaction pathway results in a negative k value which results in an imaginary frequency. This imaginary frequency is shown as a negative frequency when the frequency calculations are made using Gaussian methods. Negative frequency is not observed for the minimum as it has a non-negative force constant .[2][3][4][5][7]

Two different Gaussian methods were used to optimise the reactants, products and transition states, namely PM6 and B3LYP. PM6 is a semi-empirical method which was used to guess the location of the minimum and transition state. The DFT method B3LYP was then used to obtain a more accurate guess of the minimum and transition state. The PM6 method was used first to speed up the calculation using the second method.

Nf710 (talk) 21:45, 8 February 2018 (UTC) Your discussion about TS was not quite correct. A minimium has positive second derivatives in all directions. A TS has positive in all except one which is negative and that is the reaction coord. this is found by diaginalising the hessian at that point.

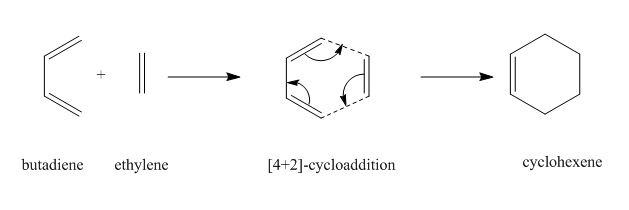
Exercise 1 - Reaction of Butadiene with Ethylene

Figure 2: Reaction scheme of the reaction of butadiene with ethylene to form cyclohexene.

(Fv611 (talk) Good section overall, but could have done with more discussion.)

Molecular orbital diagram

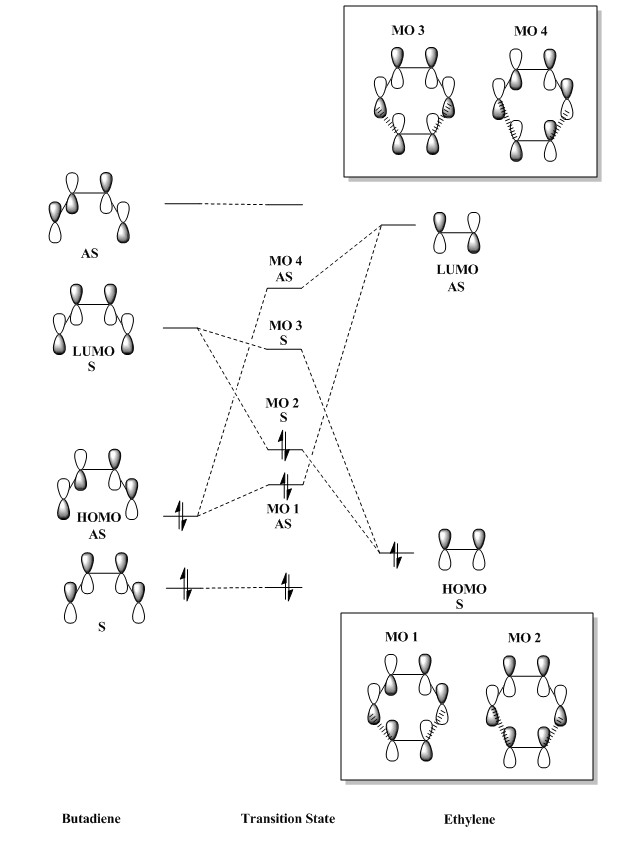
This is a Diels-Alder reaction in which the butadiene reacts with the ethylene via a [4+2]-cycloaddition reaction which breaks two pi bonds bonds and form two sigma bonds in total. Inspection of the MO diagram in Figure 3 shows that the HOMO of ethylene is lower in energy than the HOMO of butadiene. This is a characteristic of a normal electron demand Diels-Alder reaction in which the butadiene which acts as the diene is more electron-rich (higher in energy) than the ethylene which acts as the dienophile.[8]

Interaction of the molecular orbitals

Table 1 : Molecular orbitals formed at the transition state from respective HOMO and LUMO shown in horizontal order

Butadiene(LUMO)

Ethene(HOMO)

MO2

MO3

Ethene(LUMO)

Butadiene(HOMO)

MO 1

MO 4

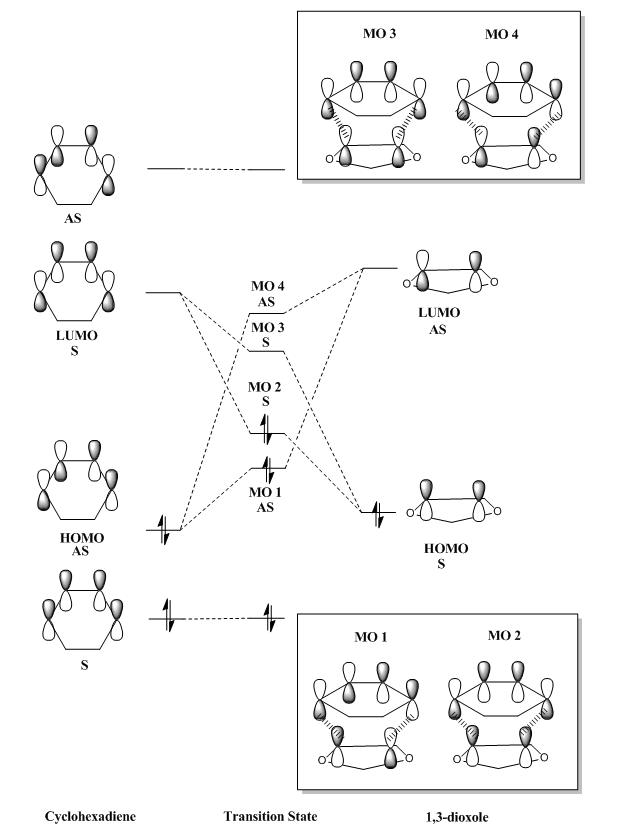
MOs 1 and 4 are formed from the combination of two antisymmetric orbitals while MOs 2 and 3 are formed from the combination of two symmetric orbitals. It can thus be concluded that a reaction is allowed when the molecules have the same symmetry. For example, HOMO of butadiene and LUMO of ethylene react because they have the same symmetry which leads to net orbital overlap and bond formation. Combination of atomic or molecular orbitals of different symmetry will lead to net orbitals overlap of zero, thus no bond formation. For example, if one of the symmetric orbital of butadiene and one of the antisymmetric orbitals of ethylene were to overlap, the in-phase combination at one orbital of ethylene cancels out the out-of-phase bonding at the other orbital. This results in a net bonding of zero. The table below shows how the orbital overlap integral changes with the symmetry of the orbitals.

Table 2 : Overlap integral produced by orbitals of and and different symmetry
Type of interaction	symmetric-antisymmetric	symmetric-symmetric	antisymmetric-antisymmetric
Orbital overlap integral	zero	non-zero	non-zero

Bond lengths and bond formation

The C-C bond lengths in the reactants, transition state and product are illustrated below.

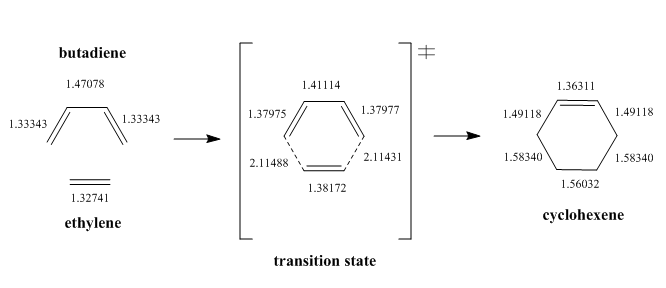
Figure 4: Bond lengths of the reactants, transition state and product. ‎

The bond lengths increase as the bond changes from a double bond to a single bond and vice versa. As the bond changes from a double bond to a single bond, the percentage of s character in the orbital increases, thus the orbital becomes less core-like. The orbital is further from the nucleus, so the bond is longer. The typical sp³ and sp² C-C bond lengths are 1.54 Å and 1.46 Å respectively.[9] The Van der Waals (VDW) radius of a carbon atom is 1.70 Å.[10] The partly formed C-C bonds in the transition state is shorter than the sum of the VDW radii of two carbon atoms (3.40 Å) but longer than a sp³ and sp² C-C bond length. This shows that the atomic orbitals of the two carbon atoms have overlapped to an extent and the single bond has been partially formed.

Vibration that corresponds to the reaction path at the transition state is illustrated below.

Figure 5: Formation of two C-C bonds in this Diels-Alder reaction.‎

As can be seen, the formation of the two C-C bonds is synchronous because both of the C-C bonds form at the same time.

Files

File:JR3915CYCLOHEXENE.LOG

File:JR3915CYCLOHEXENE TS.LOG

File:JR3915CYCLOHEXENE IRC.LOG

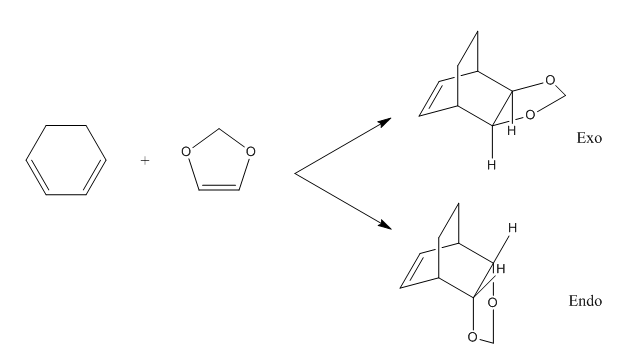
Exercise 2- Reaction of Cyclohexadiene and 1,3-Dioxole

Figure 6: Reaction scheme of the reaction of cyclohexadiene with 1,3-dioxole to form a bicyclo[2.2.2]octane adduct.

Molecular orbital diagram

(Fv611 (talk) You don't include the LOG file for your diene, so I wasn't able to check whether the calculation was done properly, but the LUMO of the diene is actually lower in energy than the TS LUMO. Additionally, you haven't discussed at all the look of the MO diagram for the endo reaction.)

Molecular orbitals determined based on symmetry

This is an example of a slightly complex Diels-Alder reaction where the formation of two products are possible depending on the orientation of the 1,3-Dioxole during the attack.If the oxygen atoms in dioxole point away from the diene, it forms an exo product while if the oxygen atoms point towards the diene, it forms an endo product. As this is a Diels-Alder reaction as well, the occupied and unoccupied molecular orbitals could be found by the symmetry shown by MOs 1-4 in Figure 3. The MOs follow a AS, S, S, AS pattern where the first two MOs are occupied and the later two are unoccupied. The corresponding MOs for both exo and endo TS are shown below in Table 3 and Table 4.

Table 3 : Occupied and unoccupied molecular orbitals associated with the Exo-TS

MO1

MO2

MO 3

MO 4

Table 4 : Occupied and unoccupied molecular orbitals associated with the Endo-TS

MO1

MO2

MO 3

MO 4

Single point energy calculation

A single point energy calculation allows the energy levels of the HOMO and LUMO of the butadiene and ethylene to be known. MOs 1-4 shown below are arranged in increasing order of energy values.

Table 5 : MOs obtained using Single Energy Point calculation showing HOMOs and LUMOs in the reactants

HOMO of cyclohexene (MO 1)

HOMO of 1,3-Dioxole (MO 2)

LUMO of cyclohexene (MO 3)

LUMO of 1,3-Dioxole (MO 4)

Since the HOMO of the 1,3-dioxole is higher in energy than the HOMO of cyclohexene, this is an inverse demand Diels-Alder reaction.[8] The HOMO of 1,3-dioxole is higher in energy than the HOMO of the cyclohexadiene due to the donation of electrons by the oxygen atoms via its lone pair of electrons into the pi-system of ethylene making it electron-rich.

Nf710 (talk) 21:49, 8 February 2018 (UTC) Well done for doing this!. you coudl have put the energies in a table or have them come up on the jmol.

Thermochemistry

The energies (Gibbs free energies) of the reactants, transition states and products of the endo and exo reactions are tabulated below. An interesting point to note is that it was found that the exo and endo products can have two different energies according to their geometries(when symmetry was slightly broken). It was deduced that two local minima exist for each of this product where one of them is lower in energy than the other. The products at these minima differ very slightly in energy, so only one of them is included in the table below.

Table 6 : Activation energies
Reactant/TS/Product	Energy(kJ mol^-1)
Cyclohexadiene	-0.612593×10^6
Dioxole	-0.701189×10^6
Sum of the energies of reactants	-1.313782×10^6
Endo TS	-1.313622×10^6
Exo TS	-1.313614×10^6
Endo product	-1.313849× 10^6
Exo product	-1.313846× 10^6

Table 7 : Activation energy and reaction energy of the reactions
Type of reaction	Activation energy(kJ mol^-1)	Reaction energy(kJ mol^-1)
Exo	168	-64
Endo	160	-67

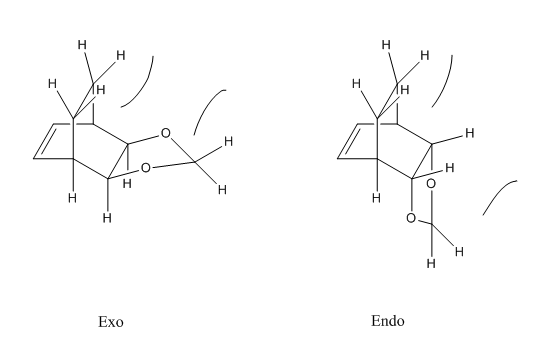
Thus, the endo-product is both the kinetically and thermodynamically stable product.It is kinetically more stable because the reaction has a lower activation energy as a result of the secondary orbital interaction between the p orbitals of the oxygen atoms and the orbitals on the 6-membered ring which is absent in the exo- product. This interaction can be seen in the HOMO of the endo transition state shown in Table 8. The endo product is also the thermodynamically stable product because there is less steric clash between the hydrogen atoms because they are further away compared to the hydrogen atoms in the exo product. This steric clash is illustrated in Figure 8.

Figure 8: Molecular orbital diagram for the formation of the TS of the exo product with the symmetry of the orbitals shown.

Table 8 : HOMOs of the endo and exo products

HOMO of the TS of endo product showing the secondary orbital interaction

HOMO of the TS of exo product showing absence of the secondary orbital interaction

Nf710 (talk) 21:51, 8 February 2018 (UTC) This was a very good section, good diagrams and Jmols. best to keep your energies to 2 decimal places. guassian has that accuracy. well done for determining the electron demand of the reaction.

Files

File:JR3915CYCLOHEXADIENE B3LYP OPTIMISATION.LOG

File:JR3915DIOXOLE B3LYP OPTIMISATION.LOG

File:JR3915NEW EXO PRODUCT 631G.LOG

File:JR3915 NEW ENDO PRODUCT.LOG

File:JR3915 NEW IRC EXO.LOG

File:JR3915IRC PM6 ENDO INITIAL PRODUCT FROZEN TS.LOG

Exercise 3-Diels-Alder vs Cheletropic

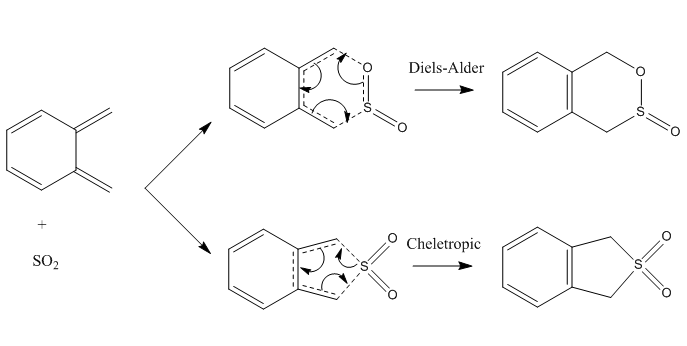
Figure 9: Reaction scheme of the reaction of o-Xylylene with sulphur dioxide.

The reaction between o-xylylene and sulphur dioxide can proceed via two pathways as shown. The Diels-Alder reaction can also take place at the other diene present in o-xylylene and this reaction is detailed in the alternative pathway section.

Reaction Coordinate

The bond formations in these three paths are illustrated below. The exo product forms when one of the oxygen atoms on the sulphur dioxide points away from the xylylene ring and vice versa for endo product. Both the exo and endo products form a stable 6-membered ring. The cheletropic reaction forms a 5-membered ring.This reaction proceeds only when the oxygen atoms are pointing away from the ring. In the case of the two oxygen atoms pointing towards the ring, the steric clash between the oxygen atoms and the ring is too great that the reaction fails to proceed.

(Interesting. Did you try this? I would imagine there are no accessible orbitals from the sulfur atom in this configuration Tam10 (talk) 13:15, 4 February 2018 (UTC))

Figure 10: Asynchronous formation of two C-C bonds in this exo Diels-Alder reaction.‎

Figure 11: Asynchronous formation of two C-C bonds in this endo Diels-Alder reaction.‎

Figure 12: Synchronous formation of two C-C bonds in this cheletropic reaction.‎

Thermochemistry

The energies (Gibbs free energies) of the reactants, transition states and products of the endo and exo reactions are tabulated below.

Table 9 : Gibbs free energies
Reactant/TS/Product	Energy(kJ mol^-1)
Xylylene	467.350
Sulphur dioxide	-311.421
Sum of energy of the reactants	155.929
Endo product	56.950
Exo Product	56.367
Endo TS	237.776
Exo TS	241.748
Cheletropic Product	0.0180
Cheletropic TS	260.095

Energy profile diagram consisting of all three pathways are shown below. The activation energies and reaction energies are shown as well.

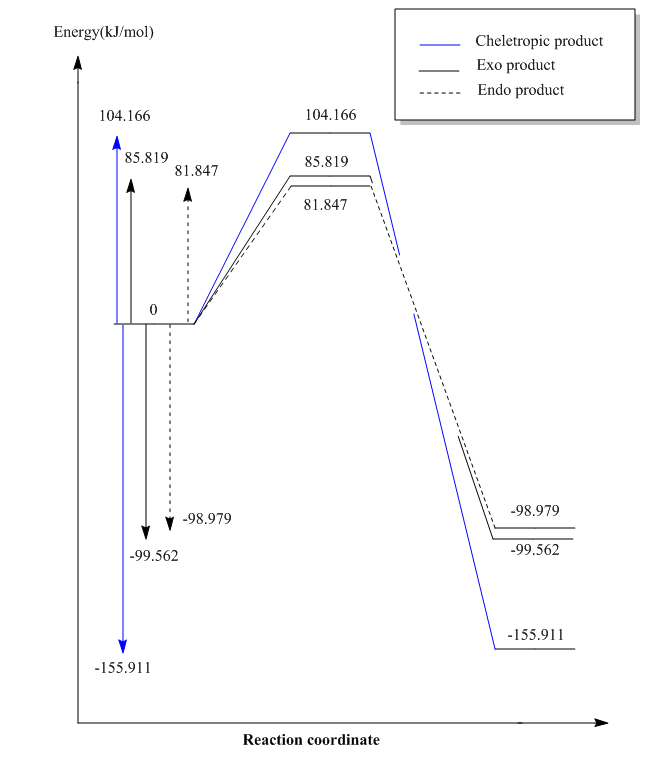
It can be seen that the endo product is more kinetically stable than the exo product because it has a smaller activation energy. This is due to the secondary orbital interaction between the oxygen atom and the ring. The exo product is however more thermodynamically stable than the endo product because the oxygen atom which points away from the ring has smaller steric clash with the ring. The cheletropic product is the least kinetically stable and most thermodynamically stable among the three products. D.Suarez and co-workers have reported that the thermodynamic stability of the cheletropic product is due to negligible charge transfer between the reactants compared to large net charge transfer in the Diels-Alder reaction.[11] It could also be due to entropic reasons where the presence of an extra oxygen atom which is not part of the ring in the cheletropic product make the molecule have higher degrees of freedom, thus higher degree of disorder and higher entropy which is thermodynamically favourable.

During the reaction , the cyclohexadiene which initially has 4π electrons gains two more π electrons when sulphur dioxide attacks and the 6π electrons become delocalised around the 6-membered ring. Owing to the Huckel's rule, the 6-membered ring gains aromaticity which makes it stable. All the three pathways are exothermic, most probably due to the stability gained from the formation of an aromatic ring.

Alternative Pathway

Exo and endo Diels-Alder can also happen at the other diene in xylylene as shown in Figure 15 and Figure 16 respectively.

Figure 15: Asynchronous formation of two C-C bonds in this exo Diels-Alder reaction.‎

Figure 16: Asynchronous formation of two C-C bonds in this endo Diels-Alder reaction.‎

Table 10 : Gibbs free energies
Reactant/TS/Product	Energy(kJ mol^-1)
Endo product	172.2511785
Exo Product	176.706652
Endo TS	267.984785
Exo TS	275.819277

Table 11 : Activation energy and reaction energy of the reactions
Type of reaction	Activation energy(kJ mol^-1)	Reaction energy(kJ mol^-1)
Exo	119.890	20.778
Endo	112.056	16.322

Both the exo and endo reactions are endothermic reactions which need input of energy for the reaction to happen. The activation energy is about 35 kJ mol^-1 higher than the other Diels-Alder reaction. Thus, the reaction at this site is both kinetically and thermodynamically unfavourable. In both cases, there is large steric clash of the sulphur dioxide with the H atoms on the ring. Also, the aromaticity of the ring is not achieved in this case as the previous one, making the reactions not energetically feasible(endothermic).

(I don't think sterics play such a role here. The important things are the distortion and lack of aromaticity in the product. Tam10 (talk) 13:15, 4 February 2018 (UTC))

Files

File:JR3915 XYLYLENE .LOG

File:JR3915SO2.LOG

File:JR3915EXO PRODUCT OPTIMISATION.LOG

File:JR3915EXO TS.LOG

File:JR3915ENDOINITIAL PRODUCT OPTIMISATION.LOG

File:JR3915ENDOINITIAL PRODUCT TS OPTIMISATION.LOG

File:JR3915CHEL INITIAL PRODUCT OPTIMISATION.LOG

File:JR3915CHEL TS INITIAL PRODUCT OPTIMISATION.LOG

File:JR3915 ALTERNATIVE EXO-PRODUCT.LOG

File:JR3915 ALTERNATIVE EXO-TS.LOG

File:JR3915 ALTERNATIVE ENDO-PRODUCT.LOG

File:JR3915 ALTERNATIVE ENDO-TS.LOG

Conclusion

PM6 method was successfully used to optimise the reactants, transition states and products in all three exercises. B3LYP method was used in Exercise 2 as well. The minimum and the transition state were differentiated by the presence of a negative frequency in the transition state optimisation. MO diagrams were drawn based on the relative energies of the orbitals. IRC calculation was carried out to study the bond formation.

The reaction between butadiene and ethylene is a normal demand Diels-Alder reaction. Orbitals must be of the same symmetry for orbital overlap integral to be non-zero and thus bonds to form. Bond length increases as the bond changes from a double bond to a single bond and vice versa. The C-C bond in the transition state has a bond length longer than a single bond but shorter than the sum of Van der Waals radii of two carbon atoms showing partially formed bonds.

The reaction betweeen cyclohexadiene and 1,3-dioxole is an inverse demand Diels-Alder reaction as the HOMO of the dienophile is higher in energy than the HOMO of the diene. Symmetry of the orbitals in Exercise 1 were used to identify the HOMOs and LUMOs in Exercise 2. The endo product is thermodynamically and kinetically more stable than the exo product because of less steric clash and secondary orbital interactions respectively.

The reaction between o-xylylene and sulphur dioxide can proceed via two different pathways-Diels-Alder and cheletropic reactions.The Diels-Alder exo product is thermodynamically more stable than the kinetic product due to less steric effect while the endo product is kinetically more stable than the exo product due to secondary orbital interactions. The cheletropic product is the most thermodynamically stable product. Aromaticity achieved by the six-membered ring makes the molecule very stable and the reaction exothermic. The Diels-Alder reaction at the other diene (alternative pathway) is not energetically feasible due to large steric clash and lack of aromaticity.

Reference

1. Lipkowitz, K. B., & Boyd, D. B. Reviews in computational chemistry. IV. John Wiley & Sons.1993.63-65 Retrieved from https://books.google.co.uk/books?id=1GnlYg_1ZRIC&pg=PA36&dq=degrees+of+freedom+in+a+potential+energy+surface+3N-6&hl=en&sa=X&ved=0ahUKEwiZk4zjg_vYAhXDJsAKHVR3CaAQ6AEIMjAC#v=onepage&q=degrees of freedom in a potential energy surface 3N-6&f=false

2.Carey, F. A., & Sundberg, R. J. Advanced organic chemistry. Part A, Structure and mechanisms.1984.175-177. Retrieved from https://books.google.co.uk/books?id=9VjtBwAAQBAJ&pg=PA176&dq=transition+state+is+the+maximum+of+a+minimum+energy+pathway&hl=en&sa=X&ved=0ahUKEwiZ1__w3frYAhWnL8AKHWHMDAgQ6AEIKjAA#v=onepage&q=transition state is the maximum of a minimum energy pathway&f=false

3.Friesner, R. A., Prigogine, I. (Ilya), & Rice, S. A. Computational methods for protein folding. Wiley.2002.364-366. Retrieved from https://books.google.co.uk/books?id=FBhtodr1Ei8C&pg=PA365&dq=transition+state+as+global+minimum&hl=en&sa=X&ved=0ahUKEwi-6eum5_rYAhUOM8AKHQVFCI0Q6AEIJzAA#v=onepage&q=transition state as global minimum&f=false

4.When Is a Minimum Not a Minimum? . Retrieved from http://www.uni-heidelberg.de/institute/fak12/AC/hofmann/acf_theo/MinNoMin.pdf

5.Ramachandran, K. I., Deepa, G., & Namboori, K. Computational chemistry and molecular modeling : principles and applications. 2008.Springer.244-246. Retrieved from https://books.google.co.uk/books?id=_imHsqknUAQC&pg=PA245&dq=transition+state+as+a+saddle+point&hl=en&sa=X&ved=0ahUKEwikxuPd5vrYAhUmIsAKHfO5AeUQ6AEINDAC#v=onepage&q=transition state as a saddle point&f=false

6.Harris, D. C., & Bertolucci, M. D. Symmetry and spectroscopy : an introduction to vibrational and electronic spectroscopy. Dover Publications.1989.104-105 Retrieved from https://books.google.co.uk/books?id=I3W6oSaRlMsC&pg=PA104&dq=hookes+law+and+harmonic+oscillator&hl=en&sa=X&ved=0ahUKEwim0NaV1f3YAhUOesAKHfIQC1gQ6AEINTAC#v=onepage&q&f=false

7.Computational physics - Finding Transition states from Saddle points - Physics Stack Exchange. Retrieved January 29, 2018, from https://physics.stackexchange.com/questions/290475/finding-transition-states-from-saddle-points

8.Dinda, B. Essentials of pericyclic and photochemical reactions. Springer.2017.44-46. Retrieved from https://books.google.co.uk/books?id=5juIDQAAQBAJ&pg=PA45&dq=normal+demand+diels+alder&hl=en&sa=X&ved=0ahUKEwjFruOr1_3YAhXmLcAKHaq7AfYQ6AEINzAD#v=onepage&q=normal demand diels alder&f=false

9.Zhou, G. Fundamentals of structural chemistry. World Scientific.1993.222. Retrieved from https://books.google.co.uk/books?id=IzDmZT6LKBMC&pg=PA222&dq=typical+sp3+and+sp2+CC+bond+lengths&hl=en&sa=X&ved=0ahUKEwiHvPeMi_jYAhXhAsAKHVEeCV0Q6AEIJzAA#v=onepage&q=typical%20sp3%20and%20sp2%20C-C%20bond%20lengths&f=false

10.Müller, U. Inorganic structural chemistry. Wiley.2007.46. Retrieved from https://books.google.co.uk/books?id=s3KlfXCY11sC&pg=PA46&dq=van+der+waals+radii+of+a+carbon+atom&hl=en&sa=X&ved=0ahUKEwj7hvyAjPjYAhUHCsAKHTubDwgQ6AEIMjAC#v=onepage&q=van der waals radii of a carbon atom&f=false

11.Sudrez, D., Sordo, T. L., & Sordo, J. A. A Comparative Analysis of the Mechanisms of Cheletropic and Diels-Alder Reactions of 1,3=Dienes with Sulfur Dioxide: Kinetic and Thermodynamic Controls. J. Org. Chem.1995.60.2848– 2852. Retrieved from http://pubs.acs.org/doi/pdf/10.1021/jo00114a039