Rep:Jed159827
Y3C - Third Year Computational Laboratory
Transition States and Reactivity - Jacob Davies
Introduction
In a potential energy surface, a minimum is a point at which the gradient is zero, and usually corresponds to the reaction coordinate of the reactants and the products, although a minimum can also be found when stable intermediates are formed during a reaction. The gradient of the potential energy surface is also zero at a maximum, such as the transition state of the reaction. This is the highest energy reaction coordinate in a potential energy surface. A vibrational frequency calculation can be completed at this point, which will give a single imaginary frequency, suggesting a negative force constant. This frequency corresponds to the change in geometry that takes place during the reaction. The following exercises investigate transition states for a series of cycloaddition reactions.
Nf710 (talk) 23:54, 11 January 2018 (UTC) You should explain this in terms of the 3N-6 (degrees of freedom) PES. A minimum has all second derivatives in the 3N-6 dimensions as positive. AS TS has in all dimensions 2nd derivatives as positive expect one which is the reaction coord. You can get this as the eigen values of the hessian matrix.
Exercise 1: Reaction of Butadiene with Ethylene
(Fv611 (talk) As a note on best practice, you should have written down somewhere that all your optimisations have been done at the B3LYP level.)
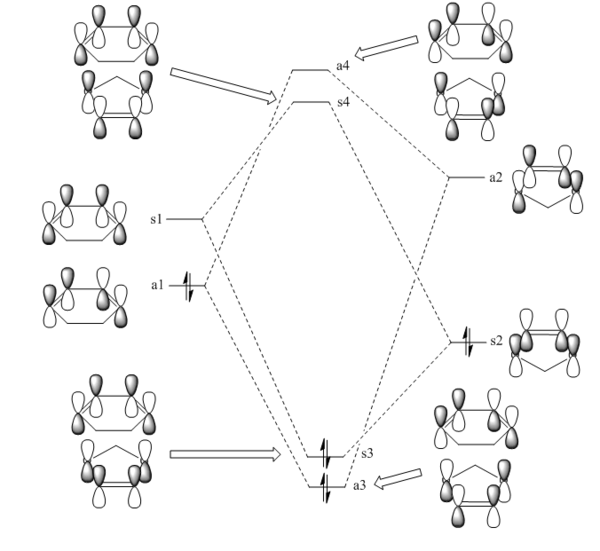
Found below is a simple MO diagram for the formation of the butadiene/ethene transition state, containing simple 'symmetric' or antisymmetric' labels, with images for the HOMO and LUMO of each of the starting reactants. The four molecular orbitals in the transition state formed from these MOs can be visualised as Jmol images below.
(Fv611 (talk) The MO combinations are correct, but the relative energies of the resulting TS MOs are not. You know from your computed TS MOs that the TS HOMO and HOMO-1 have higher energies than both the reactant MOs, so they should have been drawn accordingly on your diagram. Similarly, the TS LUMO and LUMO+1 have lower energies than the reactant LUMOs.)


Log files: File:JED15-BUTADIENE.LOG
File:JED15-ETHENE.LOG
Transition State 1 (a4)
Transition State 2 (s4)
Transition State 3 (s5)
Transition State 4 (a5)
It can be seen that for an MO on butadiene to interact with an MO on ethene, both are required to have similar symmetry. Only symmetric-symmetric and antisymmetric-antisymmetric interactions are allowed, and symmetric-antisymmetric interactions are forbidden. The orbital overlap integral is therefore non-zero for these interactions, but zero for a symmetric-antisymmetric interaction.
(Fv611 (talk) Note that the symmetry requirements are a result of the overlap integral, rather than the opposite (which you suggest): only S/S and AS/AS interactions are allowed because they are the ones resulting in a non-zero orbital integral.)
Bond Lengths
From the bond measurements below, it can be seen that the distance between the two carbon atoms forming bond on either side of the molecule decreases from 0.227nm in the transition state to 0.158nm in the final product. This is comparable to the bond expected 0.155nm sp3 C-C bond length. The Van der Waals radius of a carbon atom is equal to 0.17nm. Therfore the minimum distance required for a C-C bond to form is 0.34nm. the partly formed C-C bonds in the transition state are short enough to easily fall within this distance, allowing bond formation. The ethene double bond increases from the typical C-C double bond length of 0.133nm to a slightly longer 0.139nm in the transition state. This bond becomes a single bond in the final product, and has the expected 0.156nm bond length of an sp3 carbon. The butadiene double bonds increase to 0.138nm in the transition state and are 0.151nm in the final product. This is slightly shorter than the expected sp3 bond length, which could be attributed to the presence of the newly formed C-C double bond adjacent to these bonds.
Butadiene Bond Lengths
Ethene Bond Lengths
Transition State Bond Lengths
Product Bond Lengths
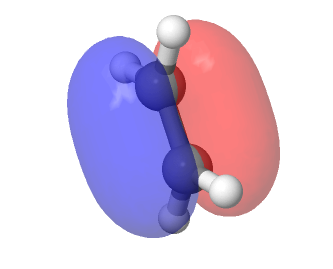
Shown above is the vibration that corresponds to the reaction path at the transition state. It corresponds to the imaginary frequency at -529.27 Hz. The formation of the two bonds is synchronous, as the carbon atoms on either side of the butadiene and ethene are moving in unison, so the bonds will be formed at the same time.
Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole
This section investigates a Diels Alder reaction, including the construction of MO diagrams, investigating whether the reaction is 'Normal' or 'Inverse Demand', and analysing the thermochemistry of the reaction. Below are all the important molecular orbitals for this reaction, and the MO diagrams for the endo and exo transition states.
(Fv611 (talk) Like in the previous exercise, you haven't paid attention to the relative energies of your calculated MOs. You are drawing product MO diagrams rather than TS ones. Additionally, there isn't much point in including two separate endo and exo MO diagrams if they look exactly the same and you don't include any discussion on the difference in relative energies across the two conformations.)
Cyclohexadiene HOMO
Cyclohexadiene LUMO
Dioxole HOMO
Dioxole LUMO
Exo Transition State MO Diagram
Exo Transition States
Transition State 1 (a3)
Transition State 2 (s3)
Transition State 3 (s4)
Transition State 4 (a4)
Endo Transition State MO Diagram
Endo Transition States
Transition State 1 (a3)
Transition State 2 (s3)
Transition State 3 (s4)
Transition State 4 (a4)
Exo Product MOs
HOMO
LUMO
Endo Product MOs
HOMO
LUMO
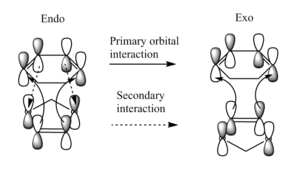
The diagram below shows that the HOMO of the endo transition state contains secondary orbital interactions between the carbon atoms at the back of cyclohexadiene and the orbitals on the oxygen atoms on dioxole. This makes the endo product the kinetic product of the reaction. The exo transition state only contains primary orbital interactions.
Normal or Inverse Demand Diels Alder
The relative energy levels of the HOMO and LUMO for both reactants were calculated to determine whether the reaction is a normal or inverse Diels Alder reaction. The reaction is a 'normal demand' reaction when the HOMO is found on the diene (cyclohexadiene). The energy levels for the HOMOs and LUMOs are found below:
| Cyclohexadiene | Dioxole |
|---|---|
| HOMO -0.20104 | HOMO -0.19197 |
| LUMO -0.01511 | LUMO -0.04242 |
Therefore, it can be seen that the HOMO for this reaction is found on the dienophile reactant, and the LUMO is found on the diene reactant. This is an inverse demand Diels Alder reaction. This can be attributed to the mesomeric effect of the two oxygen atoms on dioxole. The ether oxygen atoms can donate electrons an leads to conjugation with the carbon carbon double bond on the molecule. This leads to an increase in dioxole's π orbital's energy, making this orbital the HOMO for the reaction.
Thermochemistry
The reactants and both the exo and endo products were optimised (B3LYP/6-31G(d)) and values for the sum of electronic and thermal free energies were extracted, and tabulated below:
| Cyclohexadiene | Dioxole | Endo Product | Exo Product |
|---|---|---|---|
| -233.321033 | -267.068132 | E-500.418691 | -500.417323 |
The difference in Gibbs free energy between products and reactants will give the Gibbs free energy for the formation of the endo and exo product, revealing which is thermodynamically favoured.
Gibbs free energy for formation of endo product = -0.029559 * 2625.5 = -77.61 kJ/mol
Gibbs free energy for formation of exo product = -0.028158 * 2625.5 = -73.93 kJ/mol
The Gibbs free energy for the formation of the endo product is more negative, so this product is thermodynamically favoured.
In order to find which product is kinetically favoured, the Gibbs free energy barrier between the products and each transition state was calculated:
Gibbs free energy of endo transition state = -500.332149
Gibbs free energy of exo transition state = -500.329163
Gibbs free energy barrier for formation of endo product = 0.057016 * 2625.5 = 149.70 kJ/mol
Gibbs free energy barrier for formation of exo product = 0.060002 * 2625.5 = 157.54 kJ/mol
It can be seen that the energy barrier for the formation of the exo product is greater than for the endo product, indicating that the endo product is favoured kinetically as well as thermodynamically.
Nf710 (talk) 23:59, 11 January 2018 (UTC) You have come to the correct conclusion and nice use of diagrams to explain the SOO. However your discussion is extremely brief. you could have shown quantitatively that the reaction is Inverse by running an energy calculation with both reactants on the same PES and looking at the orbitals. Also unfortunately your energies are slightly out but you have come to the correct conclusions.
Exercise 3: Diels-Alder vs Cheletropic
This exercise investigates the reaction between xylyene and sulphur dioxide, which can undergo three different reaction pathways, via an exo or endo transition state, or via a chelotropic reaction. Each reaction path was visualised with an IRC (PM6) calculation. .gif files for each IRC are found below, and the animations can be viewed by clicking on each image. The .log files are also found below for the Transition State calculations.
Log files:
File:EXERCISE3 - JED15 - XYLYLENE - PM6 TS2.LOG
File:EXERCISE3 - JED15 - XYLYLENE ENDO - PM6 TS.LOG
File:EXERCISE3 - JED15 - CHELOTROPIC - PM6 TS.LOG
Thermochemistry - Sum of electronic and thermal Free Energies:
Xylyene= 0.178186
SO2= -0.112724
Diels-Alder endo= 0.056109
Diels-Alder exo= 0.021696
Diels-Alder TS endo = 0.092078
Diels-Alder TS exo = 0.090556
Chelotropic adduct = -0.000002
Chelotropic TS = 0.099062
Once again, the free energy change from reactants to products can be calculated by subtracting the sum of electronic and thermal free energies of the reactants from the products:
Free energy of reactants = 0.065462
Free energy change for Diels Alder endo = -0.009353 * 2625.5 = -24.56 kJ/mol
Free energy change for Diels Alder exo = -0.043766 * 2625.5 = -144.91 kJ/mol
Free energy change for Chelotropic adduct = -0.065464 * 2625.5 = -171.88 kJ/mol
(Looks like something went wrong here. Your delta free energy for endo shouldn't be that small Tam10 (talk) 12:49, 9 January 2018 (UTC))
The formation of the chelotropic adduct is the most thermodynamically favoured of the three reaction paths, with the most negative Gibbs free energy change. The formation of the exo product is slightly less favoured, and the formation of the endo product is highly disfavoured.
The height of the reaction barrier can be used to find the kinetically favoured reaction pathway:
Barrier for formation of Diels Alder endo product = 0.026616 * 2625.5 = 69.88 kJ/mol'
Barrier for formation of Diels Alder exo product = 0.025094 * 2625.5 = 65.88 kJ/mol
Barrier for formation of chelotropic adduct = 0.033600 * 2625.5 = 88.22 kJ/mol
(I don't think your SO2 was fully converged. Your energy is too high Tam10 (talk) 12:49, 9 January 2018 (UTC))
The smallest reaction barrier is found for the formation of the Diels Alder exo product, which is therefore the kinetically favoured reaction pathway. The endo product has a slightly larger barrier, but the chelotropic adduct has considerably larger barrier, making this reaction the most thermodynamically favoured, but least kinetically favoured reaction. This conclusion is supported by the following graph, showing the energy profiles for each reaction.
(This is nice, but it shows only the electronic energy. A reaction profile would show the stationary points using the values you have above Tam10 (talk) 12:49, 9 January 2018 (UTC))
For each reaction, the six membered ring on xylyene is aromatised, due to the availability of pi electrons on the two double bonds outside the ring. There is a second cis-butadiene fragment in o-xylylene, on the side of the six membered ring that can undergo a similar reaction. The two final products that can be formed are shown below:

However, the Gibbs free energy value for each product, shown below, indicates that this reaction is highly unfavourable
Endo product = 0.067302 Hartrees
Exo product = 0.065608 Hartrees
The Gibbs free energy of both of the products for this reaction pathway are higher than the Gibbs free energy of the reactants. The reaction is therefore endothermic, so is thermodynamically unfavoured. The transition state of the endo and exo product could not be optimised. However, it would be expected that the kinetic barrier would be very high, making the reaction kinetically unfavoured. The unfavourability of this mechanism can likely be attributed to the lack of an aromatic system being formed in the final product.
(Good Tam10 (talk) 12:49, 9 January 2018 (UTC))
Conclusion
These exercises demonstrate the power of computational chemistry in studying potential energy surfaces and transition states. From some relatively short and simple procedures on the computer, useful thermochemical and mechanistic information can be extracted and used to obtain useful chemical information, without the need for any complex laboratory work. However, the nature of these electrocyclic reactions that were studied lend themselves very well to this kind of analysis, due to the simplicity of the bond forming and bond breaking. In general only Carbon-Carbon bonds are being broken and formed, and the mechanisms are concerted and relatively simplistic. If a transition state needed to be analysed that was part of a more complex reaction involving different atoms and a large number of molecules, or if multiple transition states were present in a reaction, these methods may need to be developed and expanded upon to give useful results. Further work in this area could involve investigating more pericyclic reactions, such as those involving conrotation or disrotation.