Rep:Jc1506:copley03
Introduction
The Cope Rearrangement
The Cope rearrangement was developed in the 1930-40s by Arthur Cope[1]. It is generally accepted to proceed via a concerted [3,3] sigmatropic shift.
Optimizing the Reactants and Products
Both the reactant and product of the prototypical cope rearrangement is 1,5-hexadiene. This is a structure with numerous possible conformations, many of which will be similar in energy. There are multiple factors at play in determining which stucture will have the lowest energy. Firstly, there is the effect of steric strain, whereby groups close to each other in space will repel each other, leading these structures to by high in energy. Also, there is the issue of minimising dipole moment from the double bonds. Counteracting these effects is the so-called 'gauche' effect
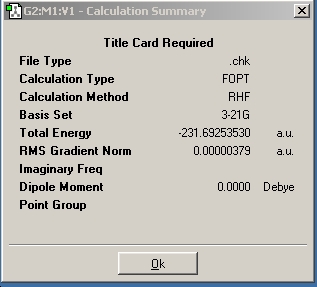
Structures can broadly be grouped into those with a gauche link and those without. Structures of both types were drawn in Gaussview and then optimized by the Hartree-Fock method and the 3-21G basis set. The checkpoint file was then opened and the "symmetrize" option used to determine the point group of the conformation drawn.
First drawn was a structure with Ci symmetry, as shown below.
Ci
The energy of this conformation matches that of identical symmetry in the lab script.
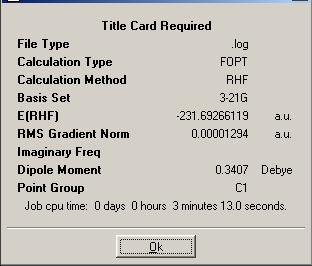
Next, for comparison, a conformation in which the dihedral angle of the central four atoms was ~60 degrees (i.e. synclinal or gauche) was drawn and optimised. This was found to have C1 symmetry. Perhaps surprisingly, this structure was found to have a lower calculated energy that the anti- Ci structure, this is likely to be due to the gauche effect at several carbons overcoming the steric raising of energy.
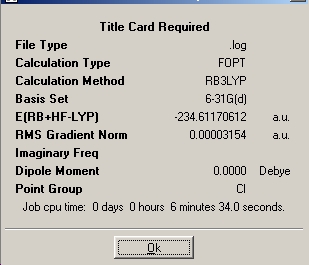
The 'anti' conformer with Ci symmetry was then reoptimised to a higher level, this time using the B3LYP method and 6-31(d) basis set.
| HF/3-21G | B3LYP/6-21(d) | |
|---|---|---|
| C=C bond length | 1.316 | 1.333 |
| central C-C bond length | 1.553 | 1.548 |
| Other C-C bond lengths | 1.509 | 1.504 |
| Central dihedral angle | 180 | 180 |
| C=C-C-C dihedral angle | 114.670 | 118.486 |
It can be seen that the C-C bond lengths change only slightly, whereas there is a relatively large change in C=C bond length and the non-central dihedral angles also change by a fairly large amount. This shows that for accurate measurements to be obtained a higher accuracy calculation is preferable, especially in small molecule situations such as this whereby computational power required is relatively small. A vibrational analysis of the 6-31* optimized structure was run, and indeed no negative frequencies were observed showing this to indeed be an energy minimum.
As these energies only represent the energy of the molecule on the bare potential energy surface, they can't be compared to experimentally observed values. This requires the addition of some extra terms, as illustrated below.
Sum of electronic and zero-point Energies= -234.469195 Sum of electronic and thermal Energies= -234.461847 Sum of electronic and thermal Enthalpies= -234.460903 Sum of electronic and thermal Free Energies= -234.500782
At 0K
Sum of electronic and zero-point Energies= -234.476093 Sum of electronic and thermal Energies= -234.468133 Sum of electronic and thermal Enthalpies= -234.467189 Sum of electronic and thermal Free Energies= -234.508804
Optimizing the Chair and Boat Transition States
In contrast to previous work, this section uses optimization techniques to find the structure of reaction transition states. As has been previously observed[2], frequency analysis of an optimized transition state structure yields one "negative frequency". It is this vibration that follows the course of the reaction.
The transition state for the Cope rearrangement must, by its nature, contain six atoms in a ring with at least partial bonding interactions between all adjacent atoms. This lends itself to the familiar 'chair' and 'boat' structures that represent the energy minima and maxima for cyclohexanes. These TS structures were optimised by various methods.
Chair Transition State
Firstly, two preoptimised allyl fragments were pasted into a chair type arrangement with the distances between non-bonded carbons set to ~2.2 Angstroms. This structure was then saved and optimised to a transition state (Berny). Force constants were calculated once and the additional keywords "Opt=NoEigen" were added to prevent the computer crashing if the guessed structure was insufficiently accurate. This job was run and the optimized structure did indeed have a negative vibration at 818 cm-1 that represented the course of the rearrangement.
This yielded a transition state structure with a distance between bond lengths of 2.020 Angstoms.
The frozen co-ordinate method was then used. This involves freezing the two bonds to be made/broken at a reasonably accurate estimate and then optimising the rest of the structure. These bonds are then unfrozen and optimised. This yielded a similar structure, but this time the transition state bond lengths were 2.021 Angstroms and the negative frequency at -817.8 cm-1
Boat Transition State
It was then attempted to draw the boat transition state in the method outlined in the script. This was drawn by the QST2 method. The structure was then drawn twice and numbered as was suggested. This opt+freq calculation failed so the structure was realigned to give a dihedral of zero degrees.
This calculation sadly failed, despite many efforts. This yielded the following structure.
The Diels-Alder Cycloaddition
Butadiene and Ethylene
Next we shall investigate perhaps the most famous and most studied of pericyclic reactions, the Diels-Alder cycloaddition. It seems appropriate to start with the prototypical Diels-Alder: the reaction between butadiene and ethylene. First, butadiene was optimised in the cis conformation using semi-empirical AM1 methods to yield a structure with the following frontier orbitals.
HOMO
Antisymmetric with respect to plane of symmetry
LUMO
Symmetric with respect to plane of symmetry
The reaction depends upon orbital symmetry with respect to the plain. It is obvious that the HOMO and LUMO of ethylene will be symmetric and antisymmetric respectively, as the HOMO consists of two in-phase p-orbitals and the LUMO two out-of-phase p-orbitals. Next, the transition state for the prototypical Diels-Alder was optimised. This was done by positioning the ethylene fragment above the terminal carbons of the butadiene fragment and constraining these interatomic distances to 2.2 Angstroms (shown earlier to be appropriate in reactions between sp2 carbons) This structure was then optimised to a minimum using AM1 methods. Then the interatomic distances were optimised giving the structure below with transition state bond lengths of 2.119 Angstroms.
The vibrational analysis was then run, with a negative frequency at -956.2 cm-1 that did indeed follow the course of the reaction
The frontier orbitals calculated are shown below
HOMO
Antisymmetric with respect to plane of symmetry
LUMO
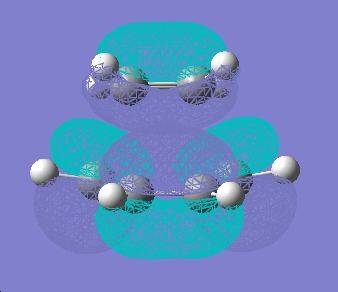Symmetric with respect to plane of symmetry
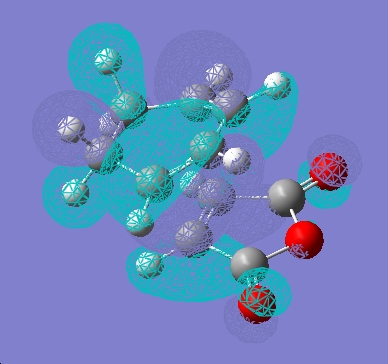
Maleic Anhydride and Cyclohexadiene
Independently, the structures of maleic anhydride and cyclohexadiene were drawn in gaussview and optimised using the AM1 semi-empirical method. The fragments were then arranged into possible exo and endo type orientations and the frozen coordinate method used as above.
| Exo | Endo | |
|---|---|---|
| Jmol | ||
| HOMO |  |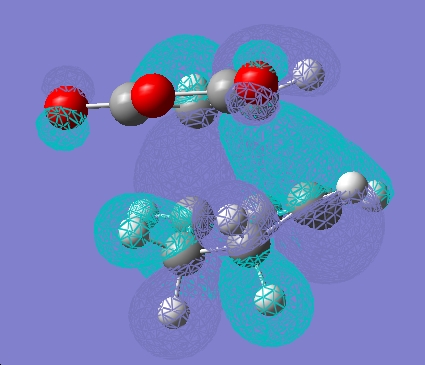
|
| LUMO | |
|
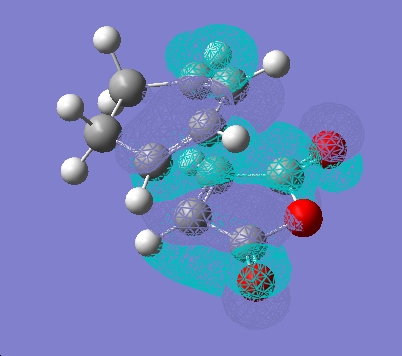
It can be seen that there is little electron density on the carbonyl atoms that are thought to be responsible for secondary orbital overlap.
Notes
- ↑ Arthur C. Cope; et al.; J. Am. Chem. Soc. 1940, 62, 441.
- ↑ Template:Https://www.ch.ic.ac.uk/wiki/index.php/Jc1506:Copley02