Transition Structures and Reactivity

Introduction

Methods

Within the exercise three different methods could be used to find the transition state. Method one, was the fastest method, however it was seldom used as it was very unreliable and required a very close approximation to the transition state. Method two, was also somewhat unreliable but was used much more than method one, and involved a 'guess' transition state and 'freezing' the atoms involved in the formation of the new bonds, this ensured that the structure drawn was a close approximation to the transition state, before optimising it. Method three involved drawing the reactants or products, which ever contained fewer molecules, and altering the bond angles and bond lengths of the atoms that are involved in the reaction. This method proved to be the most reliable and also required the least knowledge about the transition state. Throughout the exercise, all initial optimisations were initially carried out to the less expensive PM6 level before being further optimisied to the B3LYP/6-31G(d) level where appropriate. The B3LYP/6-31G(d) was not used for any first optimisations as this calculation is more accurate and precise and any initial optimisations using this method would be very time consuming.

Minimum

A minimum on the potential energy surface arises when the force constant, the second derivative of the potential energy surface, is negative. This could however only be a local minimum and does not necessarily reflect the overall minimum point of the entire potential energy surface.

Nf710 (talk) 22:21, 30 November 2017 (UTC) This is correct in 1 dimension, but the PES is in 3N-6 degrees of freedom. So the second derivative needs to be positive for all of these at a minimum on the TS. You can obtain this by diagonalizing the hessian matrix.

Transition State

The transition state is the maximum point on the potential energy surface and arises when the force constant is positive in all directions barring one, in the direction it is positive is the direction that the reaction may proceed. A frequency calculation can be used to confirm that you have arrived at the transition state, the presence of a negative frequency indicates that you have a maximum in one direction but a minimum in all others.

22:21, 30 November 2017 (UTC) OK good you mentioned more dimensions here.

Computational Methods

The PM6 method of optimisation is semi-empirical, in the method certain one-electron and some two-electron integrals from the Hamiltonian are ignored as to make the calculations less expensive to run however in their place empirical parameters are included within the calculation. Additionally, the method only considers valence electrons in any calculations and ignores the effect of core electrons within the molecule. PM6 is based upon Hartree-Fock in which a basis set of functions, the basis set is often composed of atomic orbitals, are used to represent electronic wavefunctions.

Nf710 (talk) 22:21, 30 November 2017 (UTC) Nice this is a good concise overview of PM6

The other method used through the experiment, B3LYP, is based upon Density Functional Theory, in which the energy of many-electron systems can be found by using funtionals. B3LYP is known as a 'Hybrid Functional' and is again based upon Hartree-Fock, in these functionals some of the exact exchange is from Hartree-Fock and the rest from empirical observations. DFT is based entirely upon electron density however becomes flawed when more than one electron is involved however by using B3LYP, this is corrected.

Nf710 (talk) 22:21, 30 November 2017 (UTC)'using functionals of the elctron density' .The exchange correlation term in the DFT Hamiltonian is based on HF. DFT is based on Kohn sham orbitals which are calculated wrt. the non interacting electron density. however it leaves a mystery term called the exchange correlation. different functional treat this differently. B3LYP used a Hatree fock calculation to acccount for this term and hence is now as a hybrid functional.

Exercise 1

Cyclohexene was formed via a Diels-Alder reaction between cis-butadiene and ethene.

MO Analysis

(Fv611 (talk) Very very good MO diagram. Well done! The only thing that is missing is the discussion on the overlap integral.)

The above molecular orbital diagram was produced by using PM6 optimised ethene, butadiene and transition state structures. As we know, the transition state of the reaction is the highest point in the energy profile, any of the MOs formed are higher than the Frontier Orbitals that contribute to the transition state MO. The diagram clearly illustrates mixing between the antisymmetric HOMO of butadiene with the antisymmetric LUMO of ethene, similarly the symmetric LUMO of butadiene mixes with the symmetric HOMO of ethene to produce the transition state MOs. Bonding and antibonding interactions are only observed between two Frontier Orbitals of the same symmetry, i.e. symmetric with symmetric and antisymmetric with antisymmetric.

The MOs labelled as HOMO and LUMO are the bonding and antibonding result of the overlap between the symmetric butadiene HOMO with the symmetric ethene LUMO. The above 'HOMO - 1' and 'LUMO + 1' MOs are the result of overlap between the antisymmetric butadiene LUMO and the ethene HOMO. There is a larger splitting for the butadiene LUMO and ethene HOMO resulting in larger splitting and hence the 'HOMO - 1' and 'LUMO + 1' than between the butadiene HOMO and the ethene LUMO.

The HOMO and LUMO for ethene, butadiene and the transition state, as well as the 'HOMO -1' and 'LUMO + 1' for the transition state, can be seen below.

Ethene

Butadiene

Transition State

LUMO

HOMO

LUMO + 1

-

HOMO - 1

-

Bond Length Analysis

C-C Bond	Butadiene/Ethene	Transition State	Cyclohexene
C-C Bond	C-C Bond Lengths (Å)
C1-C2	1.33522	1.50034	1.37988
C2-C3	1.46822	1.33766	1.41108
C3-C4	1.33539	1.50034	1.379780
C4-C5	-	1.54002	2.11490
C5-C6	1.32731	1.54076	1.38179
C6-C1	-	1.54004	2.11447

The notation used above for carbon i.e. C1, refer to those in the reaction scheme at the top of this section.

As expected C1-C2 and C3-C4, the two butadiene double bonds lengthen slightly during the transition state as the bond order decreases however lengthen significantly when cyclohexene is formed, compared to the initial reactants as they become single bonds and the hybridisation changes from sp2 to sp3. Similarly, C5-C6 lengthens slightly in the transition state and lengthens more in the product as the bond becomes a single bond from a double bond, again as the hybridisation changes from sp2 to sp3. The C2-C3 bond becomes shorter in the transition state as expected as the bond is becoming a double one, the bond is then significantly shorter in the products when it has full double bond character and the hybridisation of the carbons involved change from sp3 to sp2. The C4-C5 and C1-C6 lengths do not exist in the reactants as they are two separate molecules however some interaction, albeit weak however as we know the Van der Waal's radius of carbon is 1.70Å we can see that the distance between the two carbons is significantly less than 3.40Å and hence shows some bonding interaction developing. (Fv611 (talk) Yes, but how does the length of the bonds that are being formed compare with the sp3-sp3 bond length?) Overall, the single and double bonds seen in the reactants and products are typical of what we would expect to see, a typical C-C double bond is 1.33Å and a typical C-C single bond is 1.454Å, and as we can see the above bonds are very close to these values.

Vibrations

Vibration 1 above shows the imaginary vibrational frequency calculated by optimising the transition state to the PM6 level. It clearly shows the terminal carbons of the butadiene molecule and the ethene molecule moving towards one another and away from each other again. The movement is symmetric throughout, which shows that the reaction is synchrous as one would expect of a Diels-Alder reaction.

Vibration 2 shows the first real vibrational frequency, calculated to the same level. From this one can see there is no bonding interaction between either molecule and just shows some twisting.

Exercise 2

Reaction

The above reaction was a Diels-Alder [4+2]-cycloaddition between cyclohexadiene and 1,3-dioxole, in this reaction two different adducts can be formed, exo or endo, depending on the orientation of the reactants which leads to the formation of two different products as shown above. All optimisations of the above reagents, transition states and products were initially carried out at the less expensive PM6 level and then further optimised to the B3LYP level.

MOs

HOMO

LUMO

Endo TS

Exo TS

Dienophile

-

Diene

-

In this reaction, due to the presence of two oxygen atoms next to the double bond of the dieneophile donating electron density, the dieneophile has a quite high energy HOMO and LUMO. This lead to a poor interaction between the LUMO of the dieneophile with the HOMO of the diene due to a large energy gap, however there was a more significant overlap between the HOMO of the dieneophile and LUMO of the diene as these had a much similar energy. As seen above, in the HOMO of both transition states there is a larger contribution from the HOMO of the dieneophile, this can be attributed to inverse electron demand.

Nf710 (talk) 22:26, 30 November 2017 (UTC) This is the correct understanding of the electron demand of the reaction however you should have drawn an MO diagram to back this up.

Thermochemsitry

Reaction Adduct	Activation Energy (KJ/mol)	Reaction Energy
Endo	165.62	-62.30
Exo	173.46	-58.00

The table shows the activation energies and reaction energies for both the endo and exo adducts at the B3LYP level, having been initially optimised to the PM6 level. From the above results it can be seen that the exo adduct is the thermodynamic product hence if the reaction were allowed to equilibrate this adduct would dominate the composition as it is lower in energy.

For the endo product, the transition state is stabilised by secondary orbital interactions, these interactions lower the energy of the transition state, hence it requires less activation energy as seen above, and make the reaction faster in the endo- direction and more kinetically favourable. These secondary orbital interactions between the groups attached to the dienophile and on the diene, can be seen in the HOMO of the endo transition state above.

Nf710 (talk) 22:30, 30 November 2017 (UTC) I don't know what you have done with your reaction energy of the exo but it shouldn't be that low. Therefore you have unfortunately come to the wrong conclusion about thermo dynamic product. Your analysis of the kinetic product si correct though. You could have added a picture showing the SOO. Thwe rest of the report is really good but you have missed out a few important bits on this question such as the MO and it has reduced your overall mark. However you got really high mars in the other sections.

Exercise 3

Scheme

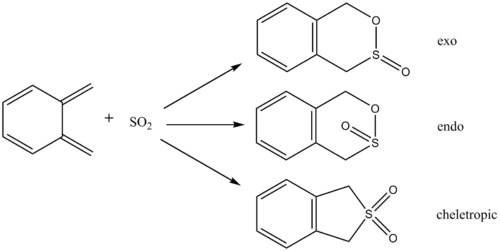
IRCs

Exo IRC	Endo IRC	Cheletropic IRC

The above gif files show that the Diels-Alder cycloaddition is asynchronous and the Cheletropic reaction is synchronous.

Note: To see either animation in motion, please click on each image.

Thermochemistry

Reaction	Activation Energy (KJ/mol)	Reaction Energy (KJ/mol)
Endo Diels-Alder	82.50	-99.21
Exo Diels-Alder	85.98	-99.86
Cheletropic	101.86	-156.17

Reaction Profile

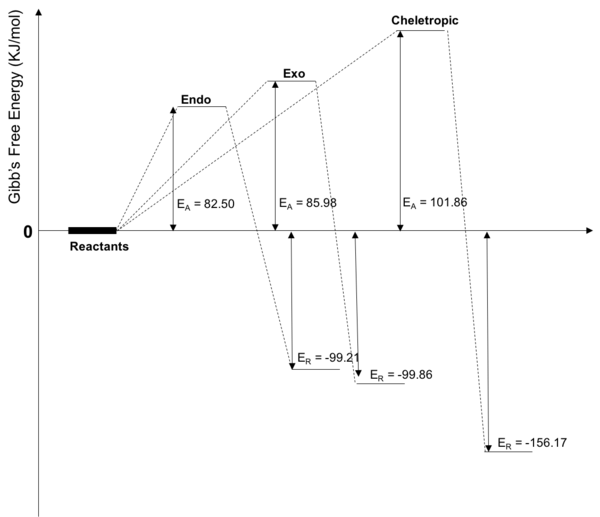
The data obtained from the .log files shows that the endo adduct is the kinetic product and that the exo adduct is the thermodynamic adduct. The relative activation energies of the three reactions can be seen above, as well as the relative reaction energies of the three reactions. As shown above, the Cheletropic reaction has the largest activation energy but also leads to the formation of the most stable product. The higher activation energy compared to the endo and exo Diels-Alder reactions is due to the formation of a more strained and less energetically favourable 5-membered ring however the ring is more stable in the product form as it contains sulfonyl, leading to it being more thermodynamically stable.

Instability of Xylylene

From the IRC animations for the endo and exo Diels-Alder reactions, one can see a delocalised pi-system forming across the ends of the diene before bond formation with the SO₂ can take place. Xylyene will react intermolecularly via an electrocyclic mechanism and will produce benzocyclobutane. The reaction, as predicted by the IRC calculations and Woodward-Hoffman rules, is thermally allowed and will happen readily. Woodward-Hoffman rules state that for a reaction to be 'thermally allowed' it must contain an odd number of (4q+2)s and (4r)a components, where s refers to suprafacial and a refers to antarafacial. In this instance, we have four pi-electrons which react in an antarafacial manner hence the reaction is thermally allowed.

(The formation of benzocyclobutene is an intramolecular reaction. Did you run this calculation? Tam10 (talk) 15:24, 27 November 2017 (UTC))

Other Diels-Alder reaction

The SO₂ molecule can react with the non-terminal diene located xylyene as well as the terminal diene, although this reaction can theoretically happen it is often disfavoured compared to reacting with the terminal diene as it does not have a stablising delocalised pi-system to stabilise the products. The thermochemistry, as well as an animation of this reaction, in the endo case, are shown below.

Reaction	Activation Energy (KJ/mol)	Reaction Energy (KJ/mol)
Endo Diels-Alder	111.80	3.84

Conclusion

Through the exercise it was found that a direct attempt at finding the transition state of a reaction is a very unreliable method of trying to find it, especially when the transition state is important. Additionally, it was found that the PM6 level was suitable for initial optimisations and rapidly reduced the time of subsequent B3LYP optimisations however the initial PM6 calculations were not accurate enough for quantitative comparisons.

Refrences

1. J. Clayden, N. Greeves and S. Warren, Organic Chemistry, 2^nd edition, 2001.