Rep:Jag115 MgO
Introduction
The experiment determines the the thermal expansion coefficient of crystalline Magnesium Oxide using computational calculations. The GULP (General Utility Lattice Program) was used to find the Helmholtz free energy and the volume of a unit cell, to determine α, the thermal expansion coefficient. The energies and unit cell volumes were calculated using two types of simulations; they were first calculated within the Quasi Harmonic Approximation (QHA) and the energies were subsequently recalculated using Molecular Dynamics (MD).
QHA relies on the fact that the Leonard-Jones potential can be viewed as a parabola with energies around those of the equilibrium energy, the zero-point energy. An issue with the QHA and its use for calculating thermal expansions is that it assumes a constant volume which we know not to be true and would also predict no actual expansion, to circumvent this issue QHA assumes that the vibrations of phonons within the approximation are volume dependent hence QHA can be used to approximate the thermal expansion.
MD is based upon classical Newton mechanics and simulates the interactions between ions within cells over a certain period of time. Each ions is assigned a specific velocity and in this instance, with gaps of 1 femtosecond, new positions for each ion were found and these were then used to solve the Schrödinger equation. A key difference between the two types of simulations ran is that in the QHA approach a Primitive Unit Cell is used, i.e. one that contains only one lattice point however in MD there is a 'supercell' containing 64 ions. Had only one cell been used in the MD approach, the simulation would have more closely represented of completely in-phase motion so a greater number of cells were used as to simulate a larger, infinite lattice.
In both the QHA and MD simulations, α was determined by using the following equation:

In the above equation, V0 is the initial volume of the unit cell at the lower temperature.
The crystalline MgO has a Face Centred Cubic (FCC) structure in real space however within reciprocal space it had a Body Centred Cubic (BCC) structure. Reciprocal space (k-space) allows calculations of the MgO lattice using the QHA on an infinite scale whilst also not being time consuming as it would be using a real structure, this crucially relies upon the periodic nature of the infinite crystalline lattice. The GULP programme is able to convert between a real space and reciprocal space, within the k-space, the k-vector describes the vibrations of the phonos with the following relationship:

Results and Discussion
Phonon Dispersion Curve and Phonon Density of States
The Phonon Dispersion Curve can be related to the Phonon Density of States (DOS) for the 1x1x1 grid. The computed DOS for the 1x1x1 grid results in one k-point which has vibrational frequencies, we can then use these vibrational frequencies to determine the position within reciprocal space. Figure 1 below, shows the Phonon Dispersion Curve and Figure 2 shows the Phonon Density of States for the 1x1x1 grid.


The 1x1x1 grid is computed for point L within the k-space, this is evident by comparing the Phonon Dispersion Curve and the Phonon Density of States. By looking at the Phonon Density of States, there are four peaks at four different frequencies, when comparing with the Phonon Dispersion Curve and reading-off at point L, point L intersects with four different curves which correspond to the frequencies of the peaks in the Phonon Density of States. Of the six branches in the Phonon Dispersion Curve, three are acoustic and three are optical, an acoustic phonon is due to the in-phase movements of atoms within the lattice away from their equilibrium positions where as optical phonons are caused by out of phase movements of atoms, i.e. one to the right and its neighbour to the left, which can only occur in lattices where the unit cells has two or more atoms. If the curves are traced back, it is apparent that two of the curves were originally two different curves that merged together, within the Phonon Density of States these two correspond to the lower frequency peaks, which have twice the amplitude of the higher frequency peaks, inspecting the log file of the Phonon Density of States simulation reveals two doubly degenerate frequencies corresponding to the peaks at 288.49cm-1 and 351.75cm-1 which correspond to the larger peaks, these are two singly degenerate frequencies within the log file which correspond to the peaks at 676.23cm-1 and 818.82cm-1, these correspond to the point (0.5, 0.5, 0.5) within the k-space i.e. point L on the Phonon Dispersion Curve.
Grid Size
As expected, increasing the grid size for the Phonon Density of States simulations increases the resolution of the plots produced, as seen below. It was found that the optimal grid size to be used was 16x16x16, increasing the grid size beyond this did not increase the resolution of the plot but increased the time taken for the simulations to be computed.
When considering other crystalline systems, the most important factor is the size of the ions involved, when finding an optimal grid size. If a crystal structure of a similar size is used i.e. CaO then it would be appropriate to use a a grid size similar to that used for MgO, CaO would be a slightly larger structure than MgO however this is only a small difference, the Ca2+ ions are still smaller than the O2- ions. If a larger crystal was modelled e.g. Zeolite, to achieve the same resolution as seen above, one would be able to use a smaller grid size, Zeolite is a larger crystal and hence in k-space it will occupy a smaller volume hence a smaller grid size would be required. The opposite is also true, if a smaller ion was used, e.g. Li+, this would occupy a larger volume within k-space and would require a larger grid size to obtain the same resolution.
Grid Size energy for Quasi Harmonic Approximation
The grid size was changed within the GULP program when determining the energy of the grid within the QHA, the temperature for the simulation was set to be 300K and the grid size was expanded within k-space, until the energy began to converge. The results of these simulations are plotted below. It was determined that a 25x25x25 grid would be suitable for any calculations as further increases dramatically increased the time taken for simulations.

As shown above, there are some initial energy fluctuations as the grid size is changed however the energy begins to converge and there is only a very small difference between the 10x10x10 grid and the 25x25x25 grid.
For calculations accurate to 1meV, a 2x2x2 grid (-40.926609eV) would be suitable, for calculations accurate to 0.5meV, a 4x4x4 grid (-40.926450eV) would be suitable and for calculations accurate to 0.1meV a 15x15x15 grid (-40.926453eV) would be suitable.
Thermal Expansion using Quasi Harmonic Approximation


As seen in Figure 10, the Lattice Parameter increases with temperature, the increase in the 0K to 1000K portion is roughly linear however beyond 1000K the Lattice Constant increases much more quickly, this effect is more pronounced as the temperature further increases. At higher temperatures the approximation breaks down as the properties of MgO change as the temperature of the simulation approaches the melting point of the solid. Figure 11 shows increased temperature leads to a decrease in the free energy of the cell, the decrease is initially small however decreases more rapidly as temperature is increased. Both of the trends of more pronounced increases and decreases can be explained by the following equation:
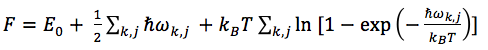
At lower temperatures, the zero point energy term of Equation 3 provides the larger contribution to the Helmholtz Free energy however as the temperature is increased, to above 1000K, the entropic term within the equation becomes more dominant and the free energy of the cell decreases more rapidly.

The above figure shows the variation of the Thermal Expansion Coefficient for the QHA and for the found literature values. In all instances, the literature values found are lower than those found experimentally however the differences are not too large. At 400K, the literature value is reported to be 1.202x10-5K-1 and was experimentally determined to be 2.25Kx10-5K-1, the experimental value is over double the literature value however as temperature is increased, both the experimental and literature values increase at a similar rate. There are approximations within the QHA that affect the values of Thermal Expansion Coefficient calculated; this includes that the approximation only simulates small oscillations from the equilibrium positions of the ions which subsequently causes problems with larger ionic separations. Additionally, the QHA will always assume that the ions are a lattice however beyond the melting point of the solid, this will not be the case.
Molecular Dynamics


As both of the above show, for the MD simulation, the Conventional Cell Volume increases roughly linearly with temperature to around 1500K, beyond this temperature there are significant deviations from a linear fit and in some cases the volume of the conventional cell decreases despite an increased temperature, we would not theoretically expect this to be the case and this shows the MD simulation is somewhat unreliable at high temperatures. At these very high temperatures, approx. 2400K, the atoms that are being modelled within the lattice are of a very high kinetic energy and due to the nature of the simulation taking averages at an interval of one femtosecond their movement can me modelled to be somewhat irregular which gives rise to decreased volumes despite increased temperatures, a potential solution to this problem when running the simulations would be to increase the number of steps taken in the calculation or to shorten the interval between averages.
In comparison to the literature value, at 400K, using the MD simulation, the Thermal Expansion Coefficient was found to be 2.845x10-5K-1, this value is again similar to the literature value of 1.202x10-5K-1 however as expected is not as close as the value predicted by QHA. It is expected that the MD approximation is more suitable when a higher temperature is used, as proves to be the case. The MD simulation ignores the zero point energy contribution to the energy of the unit cell which dominates the expression at lower temperatures, hence simulations ran on MD are more reliable at elevated temperatures.
Conclusion
Through the experiment it was found using a 16x16x16 grid was optimal when running simulations using QHA. When finding the Thermal Expansion Coefficient, it was found that the QHA simulation was more suitable at low temperatures and provided a better simulation of the crystal than MD and but at higher temperatures MD was more suitable. In both simulations, at temperatures above 2000K, the approximations used fell apart somewhat as the volumes and lattice parameters calculated fell away from linearity.
References
1. A. S. M. Rao and K. Narender. Journal of Thermodynamics vol. 2014. 532-540. 2014
2. O.A. Anderson and K. Zou. J. Phys. Chem. Ref. Data vol. 19. 1990
3. P. Atkins and J.d. Paula. Atkins Physical Chemistry Chapter 12.
4. C.Y. Ho and R. E. Taylor. Thermal Expansion of Solids p. 239. 1990.
5. C. Ronchi and M. Sheindlin. Journal of Applied Physics 90, 3325, 2001.





