Rep:Ja1915 Computational 2017
Introduction
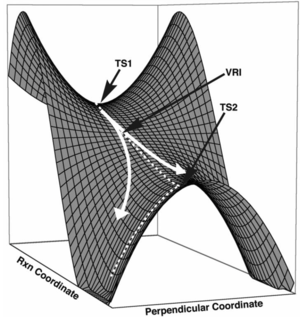
A potential energy surface (PES) maps out how the energy of the system is affected by different parameters, normally the geometry of the atoms. The potential energy surface contains stationary points (point where the surface is parallel to the horizontal line representing a positional parameter) such as a minimum point and transition states. A minimum point is a point on the PES where dE/dq = 0 (where q is a positional parameter). There are different types on minima on a PES e.g. Global minimum which is the minimum on the PES with the lowest energy or relative minimum which is a minimum only to nearly coordinates on the PES. The Intrinsic Reaction Pathway is the reaction pathway which connects the two minima together with the lowest overall energy. A transition state corresponds to a maximum along one parameter but along all other directions it is a minimum. Thus it is known as a saddle point in two dimensions. The difference between a minimum point and a transition state is that the minimum will be a minimum in all directions yet the transition state is a maximum in one and a minimum in the others i.e. the gradients at each point are the same (first derivative) but the curvature at each point differ (second derivative):
Minimum: dE/dq = 0 for all q d2E/dq2 > 0 for all q
Transition state: dE/dq = 0 for all q d2E/dq2 > 0 for all q except along the reaction coordinate where the gradient is: d2E/dq2 < 0
where the second derivatives on the potential energy surface (d2E/dq2) is the force constant according to the harmonic approximation.
In this experiment, the structures of molecules at the transition states of various reactions were found using computational methods. A frequency calculation was used to confirm the structure is at the minimum and transition state after each of these calculations by checking if the molecule had a negative frequency. At both of these points, the force constant is negative as was described earlier. The relationship between the vibration of a molecule and the force constant is shown in equation 1 where k is the force constant and u is the reduced mass.
This relationship shows that a negative force constant would thus produce a imaginary frequency of vibration which would confirm that the transition state structure was found. This imaginary vibration would illustrate the reactive atoms in the molecule moving in accordance to the reaction pathway.
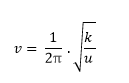
Excellent understanding of the TS and minima. You could have said how the actual corodinated used are the normal modes which are 3N-6 linear combinations of the degrees of freedom (individual bends strechs etc).
Computational methods
In this experiment, two different computational methods were utilised to optimise the structures produced: the semi-empirical method PM6 and the Density Functional Theory (DFT) method B3LYP. The PM6 method is derived from the Hartree–Fock method (an approximation for calculating the wave function by treating the Hamiltonian with respect to individual electron position). PM6 is a faster method than B3LYP because it uses values from experimental data to solve the Hamiltonian matrix to speed up the calculation, rather than calculating the integrals for each specific reaction. As a result of decreasing the computing time required to run this calculation, the accuracy of the results are compromised.
DFT method is based upon the Hartree-Fock method however it realises that the energy calculated via this method is higher than the actual value. This is because the Hartree-Fock method treats the one electron moving in the average field of other ones but does not take into account repulsion of the electrons which allow the electrons to get close to each other thus raising the energy. This therefore improves the Hartree-Fock method. However the exchange correlation part of the Hamiltonian can’t be solved via the DFT method and so is solved via the Hartree-Fock method. B3LYP is a thus hybrid method which uses DFT method but also utilises the Hartree-Fock method in order to account for the errors relating to exchange correlation. Therefore, the B3LYP method produces more accurate geometries which are more comparable to chemical data, as the method does not use pre-determined values in the calculation of the Hamiltonian matrix and does not overestimate the energy. Therefore, PM6 was first used to produce optimised structures which were then more accurately optimised using B3LYP in order to compare experimental data with literature.
Nf710 (talk) 11:28, 17 November 2017 (UTC) this is a really good paragraph, apart from saying DFT is based upon HF. It isnt it treats the hamiltonian wrt the electron density not electronic position like HF. good understanding of electronic correlation though!
The energy also depends on the size of the basis set of atomic orbitals we start with. The PM6 method has a built in basis set and so there is no choice in which atomic orbitals you choose. The atomic functions mix together to form molecular functions. This is known as Linear combination of atomic orbitals (LCAO). Variational principle is utilised to pick a set of coefficients that give the lowest energy. Mixing these atomic orbitals form a 1 electron molecular orbital (MO). These MOs can then all be added together to form a total wavefunction where the parameters are finally optimised to optimise the total energy. Again it can be seen that if more accurate basis sets are used, the calculation takes longer. The basis set used in this experiment was 6.31G(d).
Nf710 (talk) 11:28, 17 November 2017 (UTC)nice good understanding good understanding of the variation principle
Methods for finding transition state structures
In this experiment, three different methods were utilised in finding the transition structure for the different Diels-Alder reactions. Below is a description of each method used along with the advantages and disadvantages of using each method.
Method 1
Method 1 involved estimating the transition state structure of the reaction pathway and then optimising this structure using PM6 and B3LYP/6-31G(d) optimisation methods to arrive at the transition state structure.
Advantages: It is the fastest method of all three.
Disadvantages: It requires knowledge of the reaction coordinate and the transition state which isn’t always known or can be easily estimated.
Method 2
Method 2 involved again estimating the structure of the transition state and then freezing the pairs of atoms involved in the reaction. Freezing the pairs of atoms allows the other atoms to be optimised and holds the selected atoms in place (unoptimised), resulting in a much more accurate representation of the transition state being produced before optimisation of this structure occurs.
Advantages: It is more reliable than method 1 as it requires less knowledge of the transition state and it is easy to know which bonds are involved in the bond making/breaking process.
Disadvantages: As with method 1, prior knowledge of the transition state structure is needed.
Method 3
Method 3 involved optimising the product structure and then breaking the bonds formed during the reaction. The bond distances between the two structures produced were then separated before method 2 was implemented.
Advantages: The most reliable of the three methods as little knowledge of the transition state is needed.
Disadvantages: It is the slowest method of all three as there are additional steps required.
Overall for these exercises, the most useful method was method 3 as it was easier and faster to construct the product molecules and then conduct method 3 than to research the transition state structures for each reaction and then use either methods 1 or 2. As a result, method 3 was utilised for exercises 2 and 3 where as method 1 was utilised for exercise 1 as the Diels-Alder reaction covered has a heavily research transition state structure.
Exercise 1
Exercise Overview and Reaction Mechanism
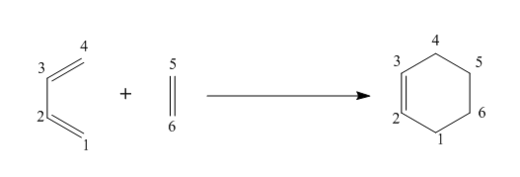 |
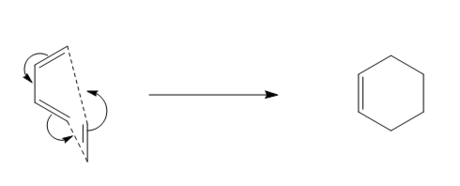 |
This exercise involved the Diels-Alder cycloaddition of s-cis butadiene and ethene forming cyclohexadiene. For this exercise, method 1 was utilised as the transition state structure for this reaction is well known and so using this method was the most efficient in terms of time. The reactants, transition state and product were all optimised at the PM6 level.
(Fv611 (talk) As you don't include a LOG file nor a JMOL of your optimised transition state structure, and as you don't mention the value of its negative frequency, there is nothing to prove that you have correctly optimised it.)
Molecular Orbital Diagram and Analysis
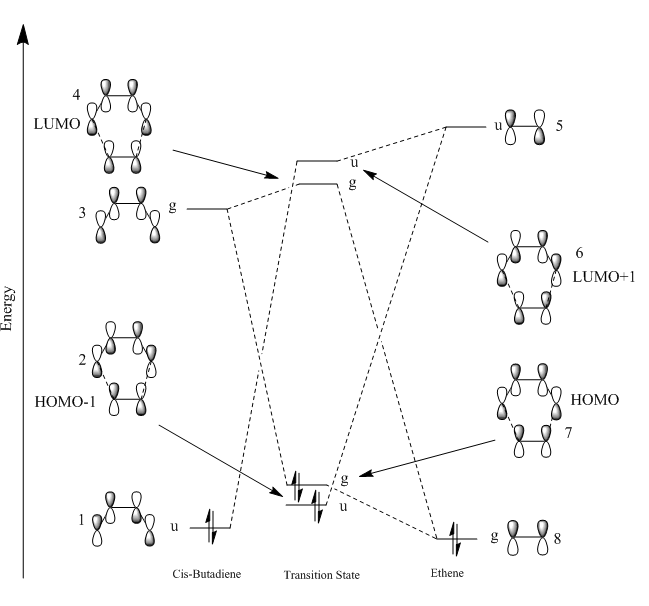
The PM6 calculation of the transition state allowed the molecular orbitals to visualised. This was then used to draw the MO diagram for the reaction of butadiene and ethene. In order for a reaction to undergo, the orbitals interacting must be of the same symmetry. This is because if they are different symmetries, they will have no net overlap i.e. produce an overlap integral of zero which therefore doesn’t lead to a reaction. When they are of the same symmetries, the overlap integral is not zero leading to the formation of bonding and anti-bonding orbitals. The electrons are then placed into the lower energy bonding orbital resulting in an overall system which is lower in energy and thus more stable. For a symmetric - antisymmetric orbital overlap, the overlap integral is zero. For symmetric-symmetric and a antisymmetric-antisymmetric orbtal overlaps, the overlap integral is not zero. Figures 7 and 6 respectively show that the HOMO of butadiene and LUMO of ethene are both antisymmetric, u (ungerade) as the orbitals undergo a change in sign upon an inversion operation. Figures 8 and 6 respectively show that the LUMO of butadiene and HOMO of ethene are again of the same symmetry, however this time they are both symmetric, g (gerade) as both orbitals don’t change sign upon an inversion operation. As a result, these orbitals will be able to mix to form an overlap integral which is not zero.
(Fv611 (talk) Your MO diagram and discussion are nice, but the labels are wrong. Molecules need to have a centre of inversion to be labelled gerade or ungerade. Should have stuck to symmetric/antisymmetric.)
In figure 4, it can be seen that the HOMO of ethene and LUMO of butadiene also overlap to form new molecular orbitals as they are close enough in energy to interact and they are of the same symmetry. Figure 4 displays the HOMO and LUMO of the transition state which shows that the reaction pathway has a normal electron demand. This is because the reaction proceeds via the HOMO of the electron rich butadiene and the LUMO from the electron deficient ethene. Proof of this is because the shapes and phases of the transition state orbitals are equivalent to the combination of these two orbitals. The sizes of the MO also correlate with this type of reaction as figure 10 shows that butadiene has a larger contribution to the bonding MO. This shows that the HOMO of butadiene is lower in energy, directly correlating with normal electron demand reactions. The transition state is defined as the point of highest energy on a reaction coordinate. Therefore the MOs that are formed as a result of the overlap at the transition state must be higher in energy than the reactant molecular orbitals. This is displayed in figure 4.
|
|
|
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
Bond Length Analysis
In Table 1, it can be seen that the single bond (C2-C3) in butadiene decreases in length due to the formation of a double bond and thus change in hybridisation of the carbon atoms. The atoms change from sp3 to sp2 hybridised which causes the bond length to decrease as there is now more s character in the hybridised orbitals. S orbitals are smaller and lower in energy than p obritals, thus they are more penetrating to the nucleus. Therefore the subsequent sp3 hybridised singma bonds are longer than sp2 hybridised single bonds as sp2 hybridised orbitals contain more s character. The double bonds in butadiene and ethene increases in length because of the breaking of the pi bond forming a single bond. The hybridisation of the carbons changes from sp2 to sp3 resulting in the formation of longer bonds as s character for the sigma bonds formed from the overlap of the carbon atoms decreases.
The Van der Waals radius of the carbon atom is approximately 1.77 Å [2]. At the transition state, the structure (seen in Table 1) shows the distance between the carbon atoms (C1-C6 and C4-C5) are 2.115 Å . As the carbon atoms are within 2 Van Der Waals radii of each other, there must be an interaction between them at the transition state.
The results of the PM6 calculation when compared with the literature values display some limitations of the PM6 method. It can be seen that the calculation produced a smaller figure for the double bond and higher figure for the single bond in comparison to literature. This highlights the fact that the PM6 model does not take into consideration the delocalisation of bonding that occurs in butadiene. Delocalisation will lengthen double bonds and shorten single bonds because the resonance hybrid (overall structure) is a combination of all resonance forms bond lengths.
| C - C Bonds | Bond Length (Å) | ||
|---|---|---|---|
| Butadiene/Ethene | Transition state | Cyclohexadiene | |
| C1 – C2 | 1.333 | 1.380 | 1.501 |
| C2 – C3 | 1.471 | 1.411 | 1.337 |
| C3 – C4 | 1.333 | 1.380 | 1.551 |
| C4 – C5 | - | 2.115 | 1.537 |
| C5 – C6 | 1.327 | 1.382 | 1.536 |
| C6 – C1 | - | 2.115 | 1.537 |
| Literature Bond Lengths (Å): Ethene: 1.331, Butadiene Double bond: 1.338, Single: 1.454 [3] | |||
Vibrational Bond Analysis
A synchronous reaction is defined as one where the extent of the reaction in terms of bond breaking and making are the same at the transition state [4]. In the case of bond formation, the two bonds must be formed to the same extent. Figure 13 displays an animation of the negative (imaginary) vibrational frequency calculated by the TS optimisation of the Diels-Alder reaction. The carbon atoms (terminal carbons on butadiene and ethene) approach each other at the same time while maintaining symmetry which means that the formation of the two bonds is synchronous. The animation in figure 13 the atoms involved in the vibration are the ones involved in the bond formation of the reaction i.e. the trajectory that the atoms are displaying is that what is expected for the production of cyclohexadiene.
Exercise 2
Exercise Overview and Reaction Mechanisms
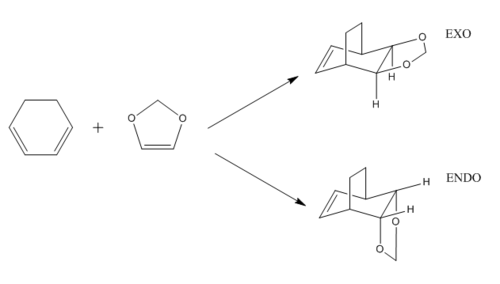
This exercise invovled the Diels-Alder cycloaddition between cyclohexadiene and 1,3-dioxole forming exo and endo products. The transition state for this structure is more complex. This coupled with the fact that the products structure could be easily constructed in Gaussian concluded in method 3 being used as this was the most reliable way of locating the transition state structure. In order to find both transition state structures, the orientation of the 1,3-Dioxole was changed to above or below the cyclohexadiene ring to change from the exo and endo reaction pathways. The reactants, transition state and product were all optimised at the PM6 level and B3LYP levels. As a result of the B3LYP calculation, this exercise was computational more expensive than exercise 1 and thus took longer.
Molecular Orbital Diagram and Analysis
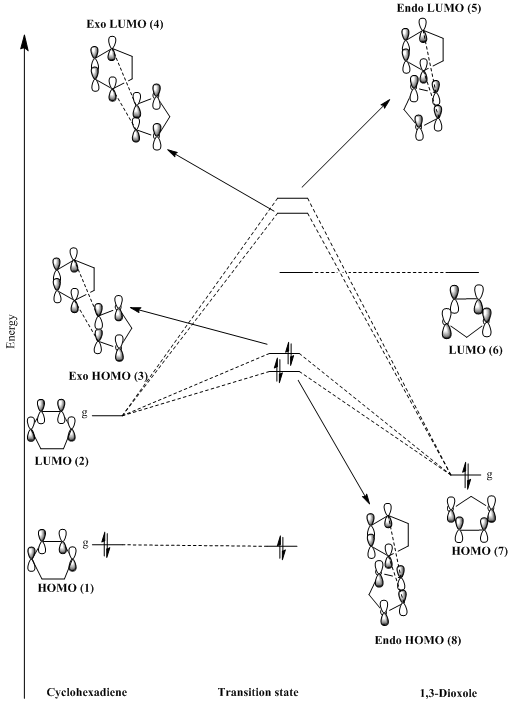
(Don't use gerade labels. That requires having a centre of inversion. Just like Rebecca's and Sophie's, you are also missing the fact that the HOMO of cyclohexadiene can interact with the LUMO of 1,3-dioxole to form 2 new MOs. Whatever you draw in the middle should appear in the TS MOs, but these non-bonding orbitals do not appear in the output of Gaussian. What you've drawn also implies the dioxole LUMO is also the LUMO of the TSs. The antibonding interaction with the CHD HOMO actually pushes it above the true LUMO. Tam10 (talk) 16:56, 12 November 2017 (UTC))
This Diels-Alder reaction is an example of an inverse electron demand reaction. This is because the dienophile (1,3-Dioxole) contains two electron donating oxygen’s where the lone pairs on the oxygen can contribute to the electron density of the double bond. As a result, the HOMO and LUMO of the dienophile are now higher in energy as displayed in the figure 15. The HOMO of the diene and LUMO of the dienophile are now further away in energy meaning that the interaction of the orbitals will be much weaker. However, the HOMO of the diene and LUMO of the dienophile are now closer in energy resulting in stronger interactions between the MO orbitals which leads to the formation of the transition state HOMO and LUMO. Therefore, this Diels-Alder cycloaddition is classed as an inverse electron demand reaction. To confirm this, a single point energy calculation was run on the transition states of each exo and endo transition states. This process ordered the MOs of each reactant in the transition state in terms of energy and illustrated that the HOMO of the dienophile was now higher in energy than the HOMO of the diene. Furthermore, the HOMO of the transition state (seen in figures 19 and 21) for both the exo and endo have a larger contribution from the HOMO of the dienophile showing it is lower in energy than the LUMO of the diene.
|
|
| |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
Thermochemistry
| Reaction pathway | Activation Energy (kJ/mol) | Reaction Energy (kJ/mol) |
|---|---|---|
| Diels-Alder Endo | 159.82 | -67.41 |
| Diels-Alder Exo | 167.04 | -63.77 |
The kinetically favoured product is the endo product as it proceeds via the lowest energy transition state. As a result, it will be formed the fastest as seen in figure 15 where the LUMO energy in the TS is lower and Table 1 where the activation energy is lower. This is because of secondary orbital interactions available in the endo orientation and not in the exo orientation (full detailed explanation below) which stabilises the endo transition state structure. The thermodynamically favoured product is the exo product because the 1,3-Dioxole ends up equatorially positioned in the product as opposed to axially positioned in the endo product. In the axial position, the molecule is higher in energy due to 1,3 diaxial interactions and gauche interactions which destabilises the product. As this is not present in the equatorial position, the exo product is thus the thermodynamic product.
Nf710 (talk) 11:31, 17 November 2017 (UTC) Noooooo This isnt correct! you worked out the energies correctly as well! Dies the exo have a larger reaction energy than the endo like you have said? what do you energies say?
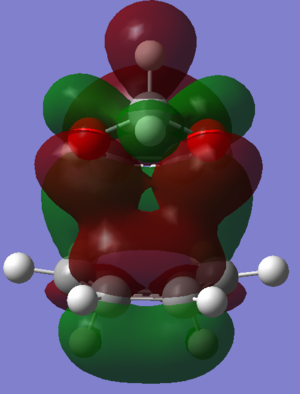
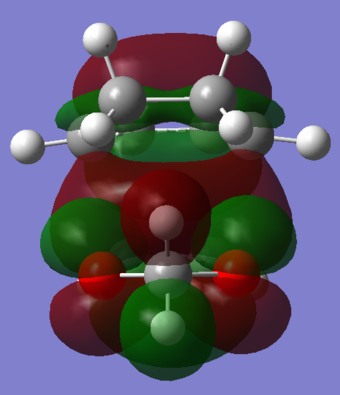
In Figures 22 and 23 it can be seen that there are secondary orbital interactions in the endo transition state HOMO but not that Exo transition state HOMO. Both oxygen atoms in 1,3-Dioxole are sp2 hybridised and so have an orthogonal P orbital which contains a lone pair of electrons. In the endo trajectory, the lone pairs in the p orbital are able to align with the pi orbitals. This favourable interaction stabilises the endo transition state and thus explains the lower activation energy for the reaction pathway towards the endo product. Secondary orbital interactions are not possible for the exo trajectory because the P orbitals from the oxygen are too far in distance from the Pi orbitals of cyclohexadiene to overlap.
This exercise also highlighted the benefits and drawbacks of the PM6 method. The thermodynamic data calculated for these reactions had the same trend in which the exo product was lower in energy than the endo product but the endo had a lower activation energy. However these values were far from the values presented in Table 2. As a result, the PM6 method can be used to determine the kinetic and thermodynamic products of a reaction but it can't be used to generate accurate data which is comparable to literature.
 |
 |
Nf710 (talk) 11:33, 17 November 2017 (UTC) Good section, your energies were correct, but you came to the wrong conclusion. Your intro was also really good.
Exercise 3
Exercise Overview and Reaction Mechanisms
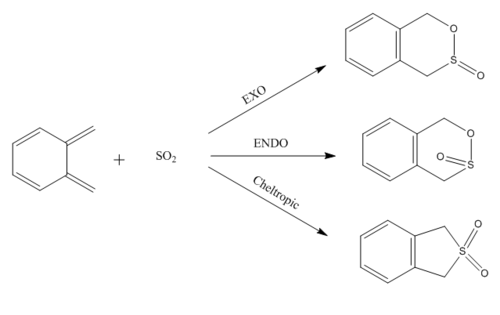
This exercise involved the Diels-Alder cycloaddition and Chelotropic reaction of o-xylelene and SO2 forming exo and endo 1,4-dihydro-2,3-benzoxathiin 3-oxide as products in the case of the Diels-Alder reaction, and 1,3-dihydrobenzo[c]thiophene-2,2-dioxide for the Chelotropic reaction. Again method 3 was utilised in this exercise as the product structure could be easily constructed. To change from the exo to endo product, the SO2 group was rotated 180° in the transition state structure. All reactants, transition states and products were optimised at the PM6 level.
IRC
An IRC was run on each transition state structure in order to visualise the reaction pathway via the bonds forming and breaking and the reaction coordinate graph showing a smooth curve.
 |
 |
 |
|---|
The reaction pathways for each reaction can be seen in these gifs by clicking on the pictures.
Thermochemistry
| Reaction pathway | Activation Energy (kJ/mol) | Reaction Energy (kJ/mol) |
|---|---|---|
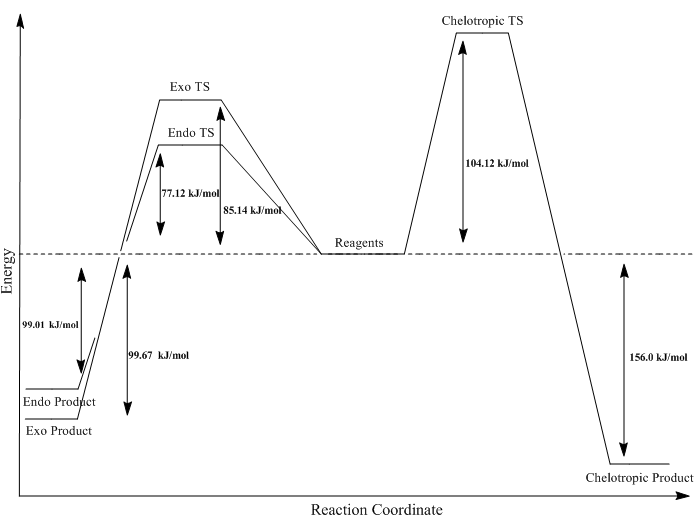
| Diels-Alder Endo | 77.12 | -99.01 |
| Diels-Alder Exo | 85.14 | -99.67 |
| Chelotropic | 104.12 | -160.0 |
From Table 4 it can be seen that as before, the endo product is the kinetic product and the exo product is the thermodynamic product. This is because the endo transition state is stabilised by secondary orbital interactions between the oxygen lone pairs on SO2 and the pi orbitals. The exo product is the the thermodynamic product as the Sulfur - Oxygen bond ends up equatorial positioned rather than in the axial. This data has also be presented on a reaction profile (Figure 28).
In Table 4, it can be seen that the reaction energy for the formation of the Chelotropic product is the lowest however the reaction pathway has the highest activation energy. The transition state for the Chelotropic reaction pathway is higher in energy due to the 5 membered ring formation which is strained as opposed to a six membered ring where all the bond angles and lengths are optimal to prevent ring strain and thus the transition state for the exo and endo are lower in energy. The product of the Chelotropic reaction is lower in energy because of the presence of the Sulfur – Oxygen double bond. This increases the enthalpic contribution towards the Gibbs free energy resulting is a lower reaction energy.
Xylelene Stability Issues
In the IRC’s of both Diels-Alder reactions, it can be seen that delocalisation of the 6 membered ring is formed first before the single bonds of the cycloaddition are formed. The Pi system formed is very stable as it is defined as aromatic with respect to Huckle’s rule (4n + 2 Pi electrons where n = 1 in this case). As a result, Xylylene is very unstable as there is a strong driving force for the reaction. This instability could potentially lead to competitive unwanted side reactions e.g. an electrocyclic reaction where benzocyclobutane is formed or a dimerisation where the molecule dimerises in a Diel-Alder cycloaddition. However it was found that the activation energy was high for the electrocyclic reaction as it required optical excitation [5]. This will be due to the formation of a strained four membered ring which increases the energy of the transition state.
An alternative Diels-Alder reaction could occur between the O-xylelene and SO2 which occurs in the six membered ring as opposed to the terminal double bonds. This reaction was investigated by calculating the transition state structures and energies which can be seen in Table 5. Here it can be seen the activation energy is higher in this reaction than the other cycloaddition. In the product, there is no aromatic stabilisation formed, as was formed in the other cycloaddition product before and so a higher transition state energy is expected as no aromatic systen would be formed throughout the reaction. However it can be seen that there will be some competing reaction present as the rate constant for this dimerisation process is 9.94 x 103 [6]
| Reaction pathway | Activation Energy (kJ/mol) |
|---|---|
| Diels-Alder Endo | 119.83 |
| Diels-Alder Exo | 111.99 |
Conclusion
The exercises highlighted how the Diels-Alder cycloaddition varies for various factors e.g. differing reactants and competing reactions. In exercises 2 and 3, the exo product was the thermodynamic product due to the position in which the new group was positioned (equatorial) and that the endo product was the kinetic product due to the secondary orbital effects. The Chelotropic product was the most stable due to its additional Sulfur - Oxygen double bond which gave a big enthalpic contribution to the reaction energy however it has the higher activation energy due to higher ring strain in the five membered ring.
The exercises also demonstrated the different computational methods one can use to find the transition state structures and which method was better in each scenario. Method 3 was the most reliable as prior knowledge of the transition state was not needed. The other methods showed a big limitation in that the transition structure must be known to a good extent before you can find an accurate transition state structure and energy. Finally, it was found that the PM6 method was fast but did not collect accurate results comparable to literature as seen in the bond angle task from exercise 1 or the thermochemistry task in exercise 2 and so B3LYP should always be used to collect accurate data on molecules.
Log files
File:Ja1915-Exercise-3-EXOPM6TS.LOG
File:Ja1915-EXOEXCERCISE3IRC.LOG
File:Ja1915-ENDOPM6EXCERCISE 3.LOG
File:Ja1915-ENDOIRCEXCERCISE3.LOG
File:Ja1915-CHELATROPICTSOPTPM6.LOG
File:Ja1915-Other-diels-ENDOPM6.LOG
File:Ja1915-Other-Diels-EXOPM6.LOG
File:Ja1915-CHELATROPICTSOPTIRC.LOG
References
- ↑ Ess, Daniel H., et al. "Bifurcations on potential energy surfaces of organic reactions." Angewandte Chemie International Edition 47.40 (2008): 7592-7601.
- ↑ Batsanov, S. S. "Van der Waals radii of elements." Inorganic materials 37.9 (2001): 871-885.
- ↑ Craig, Norman C., Peter Groner, and Donald C. McKean. "Equilibrium structures for butadiene and ethylene: compelling evidence for π-electron delocalization in butadiene." The Journal of Physical Chemistry A 110.23 (2006): 7461-7469.
- ↑ Anslyn, Eric V., and Dennis A. Dougherty. Modern physical organic chemistry. University Science Books, 2006.
- ↑ Chapman, Orville L., Robert J. McMahon, and Paul R. West. "Rearrangements of tolylmethylenes via cycloheptatetraenes: formation of benzocyclobutene and styrene." Journal of the American Chemical Society 106.25 (1984): 7973-7974.
- ↑ Trahanovsky, Walter S., and James R. Macias. "Direct observation of o-xylylene (o-quinodimethane) in solution. Dimerization kinetics of some o-quinodimethanes." Journal of the American Chemical Society 108.21 (1986): 6820-6821.
