Rep:JSheny3

Introduction

In this experiment, the reaction trajectories of three Diels-Alder reactions are investigated. Key characters of a reaction such as the location and properties of the transition states as well as activation energy and reaction energy are studied by computational methods.

Method

Gaussian is used for this experiment to optimize structure, calculate energy, run IRC and visualize MO. Two methods are used for the calculation----PM6 and B3LYP. PM6 is a semi-empirical method, which is very efficient, but often lack of accuracy. B3LYP is a method that utilizes density functional theory. In this method, repulsion between electrons are included with respect to electronic probability density. The fact that more parameters are included means that it will yield a more accurate result, yet it takes a longer time to run the calculation. In this experiment, whereas B3LYP method needs to be used, a PM6 calculation is always done first.

22:57, 30 November 2017 (UTC) Careful using the word parameters. I think you mean basis set here. if you have a bigger basis set you have more functions to build your orbitals out of. PM6 is a parameterized method and therefore doesn't do as many calculation so is faster.

Theory

A minimum of a potential energy surface is the lowest energy point. This is a point where its first derivative is zero (gradient = 0), and its second derivative is positive. To find a stationary point on a potential energy surface is relatively easy, yet to know whether it is a maxima or minima, vibrational frequencies need to be obtained. Gaussian finds the frequencies by firstly taking the second derivatives of the energy to compute the force constant.

$k = \frac{\partial^{2}}{\partial q^{2}} E$ (eq. 1)

Once the force constant is found, frequency can be calculated by treating the chemical bonds as harmonic oscillator:

$ν = \frac{1}{2 π} \sqrt{\frac{k}{μ}}$ where $μ = \frac{m_{1} m_{2}}{m_{1} + m_{2}}$ (eq. 2)

If all the vibrational frequencies are real (i.e. all force constants (k) are positive), then the structure can be confirmed as minimum.

A transition state of a potential energy surface is the highest energy point. It also has a zero gradient, but its second derivative is negative. If a structure corresponds to transition state, then its vibrational frequency should have one and only one imaginary frequency (where k in eq. 1 is negative).

Nf710 (talk) 23:01, 30 November 2017 (UTC) Ok this is correct but you haven't shown much understanding. The PES is in 3N-6 dimensions which are the degrees of freedom. A minimum has positive curvature in all of these but a TS has positive curvature in all of these except one which is the reaction coordinate.

Exercise 1: Reaction of Butadiene with Ethene

(Fv611 (talk) Good job! Could have used a bit more discussion, but your MOs and MO diagram were correct and all the calculations have been performed correctly.)

MO analysis of the reaction

The MO diagram of the formation of transition state is drawn below along with the symmetry symbol (a or s) (fig 1).

It's worth noticing that all the orbitals from the transition state are higher than the HOMO of the reactants. This is deliberately drawn in this way to show that the transition state has higher energy than the reactants in a reaction.

The HOMO and LUMO orbitals of the reactants and the orbits of transition state which they produced are listed below (table 1):

table 1: table of some key MOs and their correlation with the MO energy diagram (fig 1)

Butadiene

Ethene

Transition state of the reaction

Fig 2: HOMO

Fig 3: LUMO

Fig 4: HOMO

Fig 5: LUMO

Fig 6: MO 16 of transition state

Fig 7: MO 17 of transition state

Fig 8: MO 18 of transition state

Fig 9: MO 19 of transition state

Correlation with MO diagram (Fig1)

Figure 7 and figure 9 is a bit misleading due to the limitation of the method used for the optimization. The interactions should be between the terminal carbon atoms of butadiene and ethene like the others

From the table above, it can be concluded that only orbitals with same symmetry label can interact (either both symmetrical or both antisymmetrical). The interaction between orbitals with different symmetry (one symmetrical and the other antisymmetrical) is forbiddened. Therefore the orbital overlap integral (S) is zero for a symmetric-antisymmetric interaction and non-zero for a symmetric-symmetric/ antisymmetric-antisymmetric interaction.

(Fv611 (talk) Actually, the orbital overlap is the reason why the symmetric requirements are there, not viceversa.)

Analysis of C-C bond length and transition state vibration

The C-C bond lengths of the reactants, transition state as well as the product are listed below:

Fig 10: C-C bond lengths of ethene (reactant)

Fig 11: C-C bond lengths of butadiene (reactant)

Fig 12: C-C bond lengths of reaction transition state

Fig 13: C-C bond lengths of cyclohexene (product)

Typical sp³-sp³ C-C bond length is 1.54 Å while typical sp²-sp² C-C bond length 1.47 Å. The Van der Waals radius of the Carbon atom is 1.7 Å.

Since in the transition state, the electrons are delocalized within the two reactants, it is expected that the sp³-sp³ C-C bond of the reactants will possess higher electron density and thus the bond length will be shorter in the transition state. For the same reason, the sp²-sp² C-C bond lengths of the reactants are weaken and lengthen in the transition state. These expectations for the bond length of transitions state is verified by the above distance measurements:

C1-C4 distance in Fig 10 (1.33 Å) is shorter than C11-C14 distance in Fig 12 (1.38 Å).
C1-C4 distance in Fig 11 (1.33 Å) is longer than C9-C6 distance in Fig 12 (1.38 Å).
C4-C6 distance in Fig 11 (1.47 Å) is longer than C9-C6 distance in Fig 12 (1.41 Å).

The distance between two approaching carbons (C6 and C11 /C3 and C14 in fig 13 ) is 2.11 Å, which is shorter than the Van der Waals radius of two carbon atoms (1.7 + 1.7=3.4 Å).

(Fv611 (talk) How does the length of the bond being formed compare with the sp3-sp3 bond distance? What can you conclude from that?)

The vibration corresponds to the reaction path at transition state is shown below (fig 14):

From fig 14, it can be seen that the formation of the two bonds is synchronous, as expected for a concerted pericyclic reactions. One other way to prove this is in the transition state the distances between the two reacting carbon atoms in both ends are the same (in fig 12: C3-14 = C6-C11 = 2.11 Å).

Calculation for exercise 1

PM6 optimized reactant: Media:JSHENY3_EX1_BUTADIENE.LOG Media:JSHENY3_EX1_ETHENE.LOG

PM6 optimized product: Media:JSHENY3_EX1_OPT1_PRODUCT.LOG

PM6 optimized transition state:Media:JSHENY3_EX1_OPT1_PRODUCT.LOG

Using frequency calculation to confirm the transition state: Media:JSHENY3_EX1_OPT3_FRE.LOG

Using IRC to confirm the transition state: Media:JSHENY3_EX1_OPT4_IRC.LOG

Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

MO analysis

The MO diagram for the reaction is shown below (Fig 15 and Fig 16):

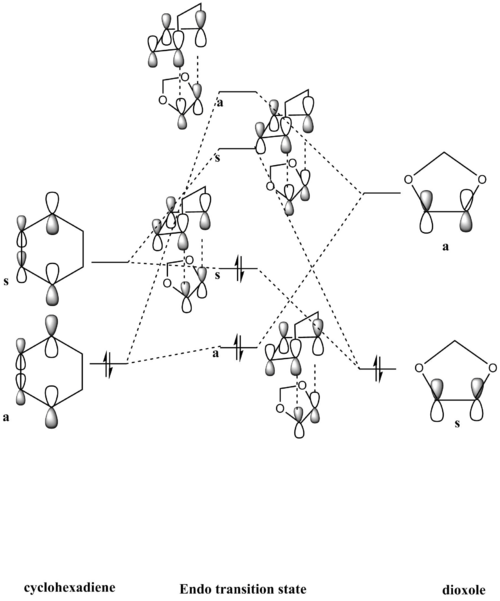
(Fv611 (talk) Good MO diagram, but you have not reported the dienophile LUMO's relative energy correctly, as that is the highest energy orbital of them all.)

The orbitals for both endo and exo transition states are listed below (table 2):

table 2: table of some key MOs and their correlation with the MO energy diagram (fig 14 and fig 15)

Endo transition state

Exo transition state

Fig 17: MO 40 of transition states (occupied)

Fig 18: MO 41 of transition states (occupied)

Fig 19: MO 42 of transition states (unoccupied)

Fig 20: MO 43 of transition states (unoccupied)

Fig 21: MO 40 of transition states (occupied)

Fig 22: MO 41 of transition states (occupied)

Fig 23: MO 42 of transition states (unoccupied)

Fig 24: MO 43 of transition states (unoccupied)

Correlation with MO diagram (Fig 15 and Fig 16)

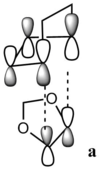
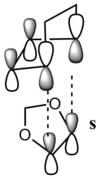
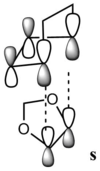
This is an inverse demand DA reaction. The inverse demand DA reaction is a [4+2] cycloaddition between an electron-rich dienophile and an electron-poor diene. In this case, cyclohexadiene (the diene) is not necessarily electron poor, yet 1,3-dioxole (the dienophile) is definitely electron-rich, due to the π-conjugation by the oxygen atoms in both ends. So 1,3-dioxole has higher energy molecular orbitals than cyclohexadiene. Therefore, it is expected that the LUMO of cyclohexadiene and HOMO of 1,3-dioxole have a smaller energy difference than the HOMO of cyclohexadiene and LUMO of 1,3-dioxole. Hence, the bonding molecular orbital formed from LUMO of cyclohexadiene and HOMO of 1,3-dioxole will be the stronger and more stable one.

Nf710 (talk) 23:09, 30 November 2017 (UTC) I wouldn't say that it is pi conjugated but the oxygens donate into the double bond raising it in energy .

This is verified by computational calculation. The HOMO, LUMO energy of both diene and dienophile can be calculated to see the energy difference (via B3YLP method). The results are displayed below (table 3).

Table 3: table of energy calculation results to show that this reaction is an inverse demand DA reaction
HOMO of cyclohexadiene	LUMO of 1,3-dioxole	Energy difference (absolute value)
-0.20554 a.u.	0.03795 a.u.	0.24349 a.u.
LUMO of cyclohexadiene	HOMO of 1,3-dioxole	Energy difference (absolute value)
-0.01711 a.u.	-0.19593 a.u.	0.17882 a.u.

So the LUMO of cyclohexadiene and HOMO of 1,3-dioxole have a smaller energy difference and therefore are better overlapped.

Nf710 (talk) 23:09, 30 November 2017 (UTC) You should only really compare the energies of theMOs when they are on the same PES

Reaction Barriers and Reaction Energy

Table 4: tabulated energies of reactants, transition states and the reaction.
	cyclohexadiene	1,3-dioxole	endo transition state	endo product	exo transition state	exo product
Sum of electronic and thermal free energies (Hartree/Particle)	-233.324375	-267.068643	-500.332150	-500.418691	-500.329168	-500.417321
Sum of electronic and thermal free energies (KJ/mol)	-6.12593193227x10⁶	-7.0118877561x10⁶	-1.31362215989x10⁷	-1.3138493733x10⁷	-1.31361433065x10⁷	-1.31384577637x10⁷

The reaction barrier of a reaction is the energy difference between the transition state and the reactants, the smaller reaction barrier reaction pathway is the kinetically favored one:
- For the endo reaction: -1.31362215989x10⁷-(-6.12593193227x10⁶+(-7.0118877561x10⁶))= 159.808946 KJ/mol
- For the exo reaction: -1.31361433065x10⁷-(-6.12593193227x10⁶+(-7.0118877561x10⁶))= 167.638188 KJ/mol

The reaction energy of a reaction is the energy difference between the product and the reactants.
- For the endo reaction: -1.3138493733x10⁷-(-6.12593193227x10⁶+(-7.0118877561x10⁶))= -67.40 KJ/mol
- For the exo reaction: -1.31384577637x10⁷-(-6.12593193227x10⁶+(-7.0118877561x10⁶))= -63.8 KJ/mol

Since the endo product is the one that has lower energy, and the endo pathway has a smaller reaction barrier, endo product is bothe kinetically and thermodynamically favored.

The HOMO of the endo and exo transition states are listed below (table 5):

table 5: table of HOMO of endo and exo transition states MO, isovalue set to 0.01

Endo transition state

Explanation

The endo transition state is the one possesses secondary orbital effect. The interaction is visualized by the figures on the left. For the endo transition state, the interaction is not just between the four reacting carbon atoms. The MOs of oxygens of 1,3-dioxole can also interact with the diene part of cyclohexadiene. Such interactions result in an overall stabilizing of transition state, and thus lower the reaction barrier of the endo transition state. However for the exo transition state, there is only primary orbital interaction between the two reactants. Therefore the endo product is the kinetically favored one.

Exo transition state

Calculation for exercise 2

B3LYP optimized endo transition state (frequency calculation is done in the same file): Media:Jsheny3 ex2 endo opt3 by3lp.log

B3LYP optimized exo transition state (frequency calculation is done in the same file): Media:JSHENY3_EX2_exo_OPT3_BY3LP.LOG

B3LYP optimized dioxole (frequency calculation is done in the same file): Media:JSHENY3_EX2_DIOXOLE_B3LYP.LOG

B3LYP optimized cyclohexadiene (frequency calculation is done in the same file): Media:JSHENY3_EX2_CYCLOHEXADIENE_B3LYP.LOG

B3LYP optimized endo product (frequency calculation is done in the same file): Media:JSHENY3_EX2_ENDO_B3LYP.LOG

B3LYP optimized exo product (frequency calculation is done in the same file): Media:jsheny3_ex2_exo_b3lyp.log

Nf710 (talk) 23:12, 30 November 2017 (UTC) Your energies are correct. this was a nice section and you shown the electron demand and the SOO nicely. It would have been good if you could have gone into more detail in the intro about the quantum mechanical methods.

Exercise 3: Diels-Alder vs Cheletropic

IRC analysis

The TSs for endo,exo and chelectropic transition states and their corresponding IRCs are tabulated below (table 6):

Table 6: Endo, exo and chelectropic (optimized by PM6) and their corresponding IRCs

Endo transition state (fig 25)

Exo transition state (fig 26)

Cheletropic transition state (fig 27)

IRC animation (click the image to see the animated reaction trajectory if it is not moving already)

TOP: IRC trajectory energy vs reaction coordinate graph, Bottom: gradient variation

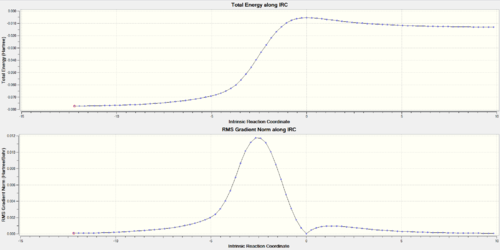
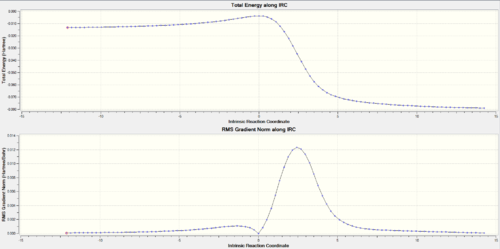
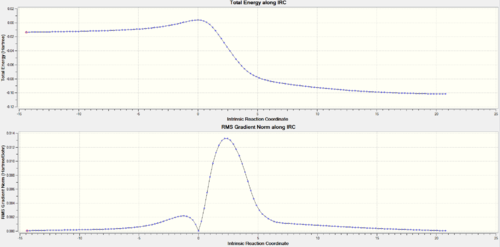
Reaction Barriers and Reaction Energy

Table 7: tabulated energies of reactants, transition states and the reaction (PM6 optimized)
	o-Xylylene	SO₂	endo transition state	endo product	exo transition state	exo product	cheletropic transition state	cheletropic product
Sum of electronic and thermal free energies (Hartree/Particle)	0.178099	-0.118614	0.090562	0.021697	0.092078	0.021454	0.099062	-0.000006
Sum of electronic and thermal free energies (KJ/mol)	467.59896	-311.4210807	237.770549	56.9654778	241.7508074	56.3274813	260.087301	-0.0157530012

The reaction barrier of a reaction is the energy difference between the transition state and the reactants, the smaller reaction barrier reaction pathway is the kinetically favored one:
- For the endo reaction: 237.770549-(467.59896+(-311.4210807))=81.59 KJ/mol
- For the exo reaction: 241.7508074-(467.59896+(-311.4210807))=85.57 KJ/mol
- For the cheletropic reaction: 260.087301-(467.59896+(-311.4210807))=103.91 KJ/mol

The reaction energy of a reaction is the energy difference between the product and the reactants.
- For the endo reaction: 56.9654778-(467.59896+(-311.4210807))=-99.21 KJ/mol
- For the exo reaction: 56.3274813-(467.59896+(-311.4210807))=-99.85 KJ/mol
- For the cheletropic reaction: -0.0157530012-(467.59896+(-311.4210807))=-156.19 KJ/mol

The endo transition state has the lowest energy and therefore the endo product is regarded as the kinetic product. The cheletropic reaction requires smallest amount of energy and therefore its product is regarded as the thermodynamically favored product.

("requires smallest amount of energy" seems to imply that you're talking about the reaction barrier. It is the thermodynamic product as the product is the lowest energy Tam10 (talk) 15:46, 27 November 2017 (UTC))

The reaction profile is drawn below (fig28):

By looking at the IRC of the reactions, it can be found that for all three reactions, the bonding of the six-membered ring changes in the same way----it gains a new double bond and forms an aromatic ring. Here, formation of endo product is used as an example:

Table 9: using formation of endo product to illustrate gaining of aromaticity by the 6-membered ring
before the reaction	after the reaction
Fig 29:	Fig 30:
number of double bonds in 6-membered ring	number of double bonds in 6-membered ring
2	3 (delocalized, showing aromaticity)

Calculation for exercise 3

PM6 optimized endo transition state: Media:SHENJY3 EX3 ENDO OPT3.LOG

PM6 optimized exo transition state: Media: SHENJY3 EX3 EXO OPT3.LOG

PM6 optimized cheletropic transition state:Media:JSHENY3 EX3 CHE OPT3.LOG

PM6 optimized endo transition state IRC: Media:SHENJY3 EX3 ENDO IRC.LOG

PM6 optimized exo transition state IRC:Media:SHENJY3 M3 IRC.LOG

PM6 optimized cheletropic transition state IRC: Media:JSHENY3 EX3 CHE IRC.LOG

PM6 optimized endo product: Media:SHENJY3 EX3 ENDO OPT1.LOG

PM6 optimized exo product:Media: SHENJY3 M3 OPT1.LOG

PM6 optimized cheletropic product:Media:JSHENY3 EX3 CHE OPT1.LOG

PM6 optimized SO₂:Media: JSHENY3 EX3 OPT SO2.LOG

PM6 optimized xylylene:Media: JSHENY3 EX3 OPT XYLYLENE.LOG

Conclusion

For computational calculation of all three reactions, the methods used give a reasonably good result. The absolute energies calculated however, are not very accurate. This can be shown in table 1 in exercise one, when interacting MOs are not correctly presented by Gaussian. Also, some of the bonding orbitals have positive energies and non-bonding orbitals have negative energies. There are possibly due to the limitation of methods used. The relative energies are quite accurate. The orders of MOs produced are what we would expect for the reaction. Using these results, some important natures of the reactions are predicted. In exercise 2, the reaction is predicted to be an inverse demand Diels Alder reaction. In both exercise 2 and 3, the kinetic and thermodynamic products are predicted. These predicted properties can be used to help design experiments in real world.