Rep:JMLOCT2015
Transition Structures and reactivity
The Cope rearrangement of 1,5-hexadiene and two Diels-Alder reactions of ‘cis-butadiene and ethylene’ and ‘cyclohexa-1,3-diene and maleic anhydride’ were analysed using the program Guassian. Transition states of the above reactions were located and their energies obtained and studied further with various methods and basis sets.
Different conformers of 1,5-hexadiene were located using HF/3-21G theory and method and the lowest energy conformer was found to be Gauche 3 (see below). The reason for this due to a favourable π / π* interaction. B3LYP/6-31G* theory level was compared to the 3-21G used; the former gave results closer to what is agreed to be accurate accounts of structure and energy. The chair and boat transition state structures of the Cope rearrangement were found using the redundant coordinate editor and the QST2 method that guessed a transition structure based on an inputted structure that had to be reasonably close to the TS. The activation energies of the rearrangement via chair and boat TS were 44.69 and 54.76 Kcal/mol respectively at 298.15 K, with HF/3-21G - showing that the calculated energies were in reasonable agreement with experimental data and that reaction via the chair TS is thermodynamically preferred.
The TS structures of the two Diels-Alder reactions were located using the redundant coordinate editor and the TS-Berny method. Evidence of secondary orbital overlap theory was observed. The activation energies of cyclohexa-1,3-diene and maleic anhydride via the exo and endo TS were calculated to be 18.46 Kcal/mol and 15.85 Kcal/mol respectively. These energies were calculated via DFT/B3LYP 6-31G* and seem to agree with secondary orbital overlap theory where the endo TS is the preferred TS to react via.
Nf710 (talk) 11:22, 19 November 2015 (UTC) Fairly good intro. It would have been nice if you could have shown some understanding of the methods such as why HF is different to DFT etc.
The Cope Rearrangement
The energy minima on the potential energy surface of 1,5-hexadiene were calculated via Gaussian. 1,5-hexadiene undergoes a [3,3]-sigmatropic shift rearrangement [1]; the different geometries and minima energies were compared using the (HF/3-21G) method to begin with.
Below is a diagram showing the two extremes of the cope rearrangement; which occur via boat and chair transition states.
 |
 |
HF/3-21G optimisations
Optimisations for 1,5-hexadiene were run via the Hartree-Fock 3-21G method where the molecule was manipulated to a structure close the desired symmetry before the method attempted to locate a minima in energy near the inputted structure. A selection of energy minima for 1,5-hexadiene were located as shown in the table below (1 hartree ~ 627.503 J).
| Conformation | Conformation | Symmetry / point group | Energy / Hartrees (HF/3-21G) | ||
|---|---|---|---|---|---|
| Anti-periplanar (1) | C2 | -231.69260233 | |||
| Gauche (3) | C1 | -231.69266122 | |||
| Anti-periplanar (2) | Ci | -231.69253517 | |||
| Anti-periplanar (3) | C2h | -231.68907 |
The lowest energy conformer
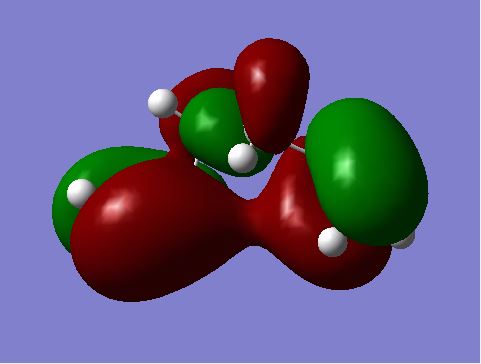
Comparing the energy of gauche (3) with anti-periplanar (1), we would expect the gauche conformation to be of slightly higher energy because of the steric hindrances / clashing the we would expect created with a gauche compared to an anti-periplanar arrangement where larger groups are not adjacent with each other. However, not only is the gauche conformation shown above lower in energy than anti-periplanar (1), it is the lowest energy conformation of a possible of 10 conformers of energy minima.[2] Gauche 3 is the lowest energy conformer because of stabilising pi-electron overlap at the ends of the molecule. This is shown in the MO diagram below of gauche 3; the pi electrons in the HOMO are overlapping, as seen in the diagram as the red orbitals overlapping - hence a lowering of energy. [3]
 |
 |
Nf710 (talk) 11:28, 19 November 2015 (UTC) Excellent use of the orbitals in the .chk to prove why the gauche is the lowest energy conf. this how we would show it in research.
Comparison to B3LYP/6-31G* for anti-periplanar (2)
Anti-periplanar (2) was chosen to compare HF/3-21G and B3LYP/6-31G* methods. The conformer was optimised with the latter method as well and then geometries were compared for the conformer. Energies from the two methods obtained were not compared since they will give meaningless comparisons.
| Conformation | Conformation | Symmetry / Point group | Energy / Hartrees (B3LYP/6-31G*) | ||
|---|---|---|---|---|---|
| Anti-periplanar (2) | Ci | -234.55970457 |
The bond lengths are compared here to help compare geometries of the the conformers after the different optimisations. The atoms were labelled as follows:
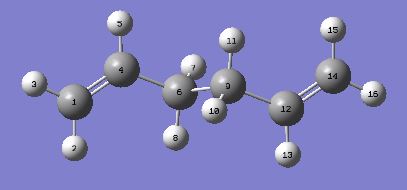
| HF/3-21G bond | HF/3-21G bond length / Å | B3LYP/6-31G* bond | B3LYP/6-31G* bond length / Å |
|---|---|---|---|
| 1 - 4 | 1.31618 | 1 - 4 | 1.33350 |
| 4 - 6 | 1.50882 | 4 - 6 | 1.50420 |
| 6 - 9 | 1.55317 | 6 - 9 | 1.54816 |
The C=C double length calculated from HF/3-21G is slightly shorter in length than the length calculated by the B3LYP/6-31G* method. The agreed literature value of C=C is 1.33 Å,[4] suggesting that the Hartree-Fock method is predicting the bond lengths to be slightly shorter. The C-C bond lengths are very similar for both methods. This suggests that the B3LYP/6-31G* method would be a more precise method to use; this is likely due to 6-31G being a more precise basis set than 3-21G. However the more precise method has a price of taking more time to run, which, again, in this system does not make a significant difference but for more complex problems it will make a difference.
The dihedral angles within the two structures were also compared as follows:
| HF/3-21G angle | HF/3-21G angle measurement / degrees | B3LYP/6-31G* angle | B3LYP/6-31G* angle measurement / degrees |
|---|---|---|---|
| 1, 4, 6, 9 | 114.626 | 1, 4, 6, 9 | 118.599 |
| 4, 6, 9, 12 | 180.000 | 4, 6, 9, 12 | 180.000 |
| 6, 9, 12, 14 | -114.654 | 6, 9, 12, 14 | -118.708 |
For a sp2 hybridised C atom, the angle is most stable at 120°. As observed above, the B3LYP/6-31G* method achieves a dihedral angle closer to 120° and the HF/3-21G method is quite far from this. Again, showing that B3LYP/6-31G* is a more precise method and so more likely to be reliable.
Nf710 (talk) 11:30, 19 November 2015 (UTC) Very very good comparison of geometries all the key degrees of freedom have been taken into account.
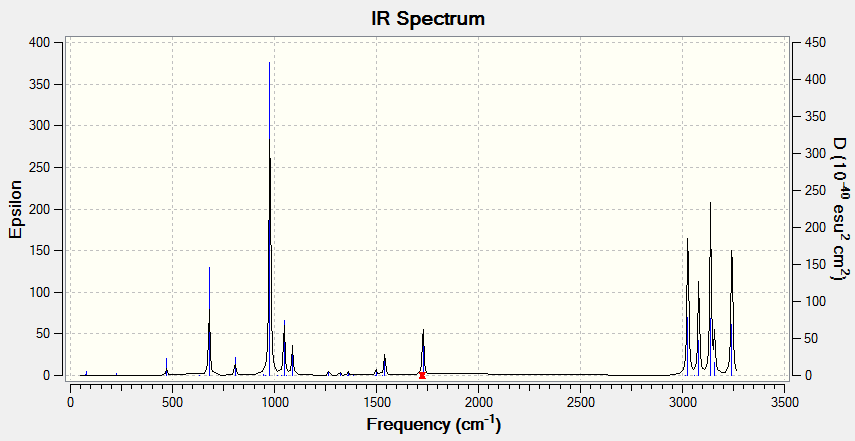
The IR frequencies of the conformer were then computed and all frequencies were real and positive. Therefore the conformer located is a minimum and not a transition state.
Below is the IR spectrum of anti-periplanar 2
More specific energies were computed for the conformer (in Hartree)
Sum of electronic and zero-point Energies= -234.416261 Sum of electronic and thermal Energies= -234.408969 Sum of electronic and thermal Enthalpies= -234.408025 Sum of electronic and thermal Free Energies= -234.447879
The sum of electronic and zero-point energies describes the potential energy at 0 K, the sum of electronic and thermal energies gives the energy at 298.15 K, 1 atm. The sum of electronic and thermal energies can be used to calculate the activation energy needed for a reaction if the energy of the transition state is found. This takes into account of the molecule's vibrational, rotational and translational energies since only at 0 K can these be ignored.
Nf710 (talk) 11:36, 19 November 2015 (UTC) energies correct
Optimising chair and boat transition structures
In the Cope rearrangement the reaction goes through a chair or a boat transition state.[5] It is expected that the chair transition state should be the preferred TS to go via as we would expect that to be the lower energy one due to steric hindrances within a boat structure.
Locating the chair TS
An optimisation of two pieces of the structure placed ~2.2 Å in HF/3-21G was run as a first guess to the chair TS structure. (Shown below)
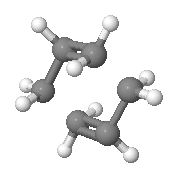
There was one imaginary frequency for the structure located, which tells us that it is a TS state and not a local minimum. Below is an animation of the imaginary frequency which is at ~ -818 cm-1
This guess for the chair TS was then optimised by freezing some coordinates at ~2.2 Å using the Redundant Coord Editor. (The distance between the two atoms where we expect bonds to be formed). The coordinates were then unfrozen and set as a derivative to be re-optimised again. The second step sometimes is unnecessary (setting the frozen bonds as the derivative); this is because sometimes the minimum structure found after freezing the coordinates is close enough to the TS structure to just run an optimisation to locate the TS. For a small system like this it does not make a significant difference in time or money; however in terms of more complex problems, differentiating along the reaction coordinate instead could be a substantial time and money saver. The following optimisations were run with HF/3-21G.
The structure after optimisation to a minimum after freezing coordinates is shown below
The structure of the chair TS optimisation after unfreezing coordinates and finding the derivative of these bonds is shown below.
Nf710 (talk) 11:55, 19 November 2015 (UTC) You have executed the frozen co ordinates well. But I don't know if you have done the TS berney. I'm going to assume that is the first part as you have done the imaginary frequency. It would have been good here if you could have shown some understanding about why it is an imaginary frequency from the force constant and the quantum harmonic oscillator.
Locating the boat TS
Next the boat transition state was attempted to be located via the QST2 method. In this method we specified the carbon numbers and so the program understood which carbon atom had rearranged where. Below are diagrams showing how the carbon atoms were numbered for the product and reactant in the rearrangement.
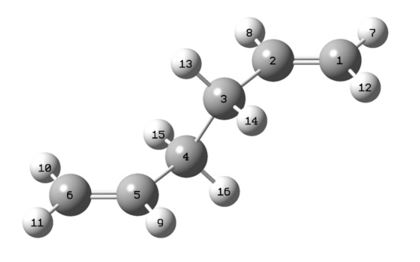 |
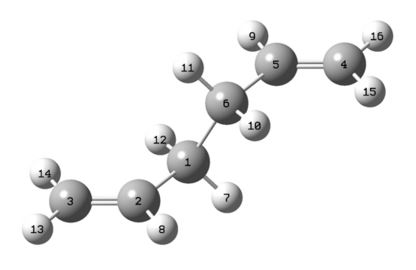 |
With the reactants and products arranged as above, they were optimised and also a frequency calculation was performed using the TS (QST2) method. The optimisation failed and a chair-like structure is located. This is because the program didn't account for the fact that there can be rotation around the central bonds within the calculation. Below is a picture of what structure was located calculating with these starting points.
For the QST2 method to locate the boat TS that we want, the starting reactant and product molecule had to be manipulated via the angles between the groups so that they are closer to the TS we want. After doing this the following TS was found, it is the boat TS.
A frequency calculation was also done on the structure and it possessed one imaginary IR frequency at -839.98 cm-1 which confirmed that the structure was a transition state structure. Below is an animation of said frequency.
The IR spectrum of the boat TS located is also shown below.
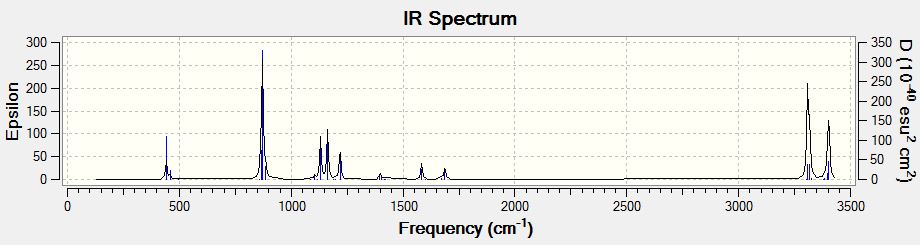
It was seen that the QST2 method is a very powerful one that didn't need the reactant and product distances 'guessed' like the previous methods. But there is a disadvantage of having the need to make sure the starting structures themselves are close enough looking to the desired TS for the method not to fail.
Locating which conformer a chair TS will lead to
You cannot tell which conformer the transition states of boat and chair lead to in the reaction by just looking at them. So an IRC calculation was run on an optimised chair TS. This tries to locate the local energy minimum and then find the lowest energy route to it. Below is the IRC plot for this:
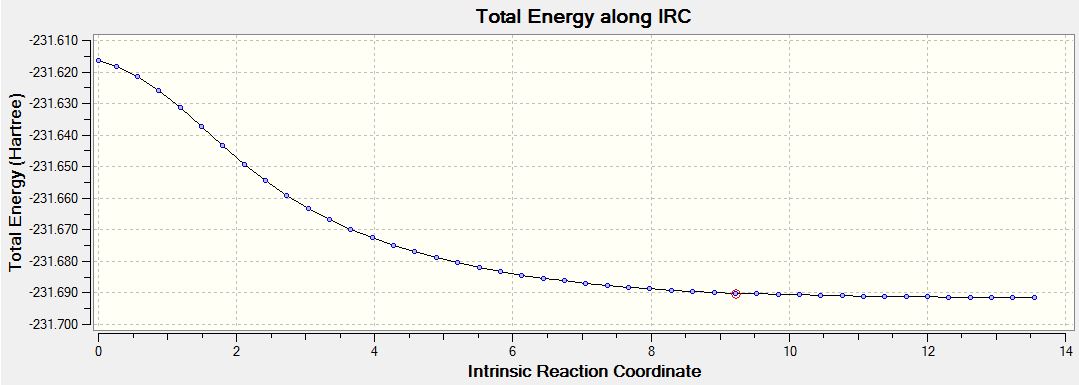
Below is the first structure after running the IRC method (going from a chair transition state to a minimum after 50 steps).
After having tried to find the local minimum of the chair TS in 50 steps the last structure was run with a normal minimisation one more time and the following structure was seen. It is clear the desired minimum has not been located.
One of the options of how to locate the minimum point is to re-run the IRC calculation but to increase the number of points. This is straightforward but very time consuming also if too many points are used then the reaction path could move in the wrong direction and the desired minimum would still not be located, in complex problems it could be expensive. Another option would be to re-run the IRC and compute the force constants for every step; this is time consuming and expensive again but it is the most accurate method.
Calculating activation enthalpies
Having computed the transition structures if the energies of the TS and reactants were subtracted then an activation energy can be calculated for the reaction. The B3lYP/6-31G* and HF/3-21G methods were compared again.
Comparison of electronic energies with HF/3-21G and B3LYP/6-31G* of boat and chair TS with anti-periplaner (2) as a reference
| HF/3-21G (Hartree) | Electronic energy | Sum of electronic and zero-point energies (0 K) | Sum of electronic and thermal energies (298.15 K) | B3lYP/6-31G* (Hartree) | Electronic energy | Sum of electronic and zero-point energies (0 K) | Sum of electronic and thermal energies (298.15 K) |
|---|---|---|---|---|---|---|---|
| Chair TS | -231.619322 | -231.466705 | -231.461346 | Chair TS | -234.556983 | -234.414919 | -234.408998 |
| Boat TS | -231.602802 | -231.450929 | -231.445300 | Boat TS | -234.543093 | -234.402340 | -234.396006 |
| Anti-periplanar 2 | -231.692535 | -231.539539 | -231.532566 | Anti-periplanar 2 | -234.611710 | -234.469203 | -234.461856 |
| HF/3-21G (KCal mol -1) 0 K | HF/3-21G (KCal mol -1) 298.15 K | B3lYP/6-31G* (KCal mol -1) 0 K | B3lYP/6-31G* (KCal mol -1) 298.15 K | Experimental (0 K) | |
|---|---|---|---|---|---|
| Chair TS, Activation enthalpy | 45.70 | 44.69 | 34.06 | 33.17 | 33.5 +/- 0.5 |
| Boat TS, Activation enthalpy | 55.60 | 54.76 | 41.96 | 41.32 | 44.7 +/- 2.0 |
The geometries of B3lYP/6-31G* and HF/3-21-G optimisations were very similar. However, the activation energies were quite different. As the B3lYP/6-31G* method is more time consuming and therefore expensive, it is reasonable that for large, complex problems that the HF/3-21G method is run first and then the results from that are re-optimised using B3lYP/6-31G*.
As seen from above, the activation enthalpies for both methods are close to the experimental values, with B3lYP/6-31G* being the better approximation.
Nf710 (talk) 12:15, 19 November 2015 (UTC) You forgot to check imaginary frequencies for your re optimised TS structures. Your energies are correct. this is a good report you have done everything asked of you. it is a shame about the IRC. You could have made it slightly better though by having a greater understanding of how the TS optimisations work and some theory into how the DFT and HF methods work. The way you used the orbitals to show the gauche as lower was very nice.
Diels-Alder cyloaddition
Diels-Alder reactions are a fundamental class of reactions in chemistry; they only require heat and have 100% atom economy. In it pi orbitals from a diene will overlap with the pi orbitals of a dieneophile and new sigma bonds will be formed. The HOMO and LUMO of the diene will interact with the HOMO and LUMO of the dieneophile during the reaction. The orbitals must be in phase / have the correct symmetry, have sufficient overlap and cause an overall decrease in energy for the reaction to take place.
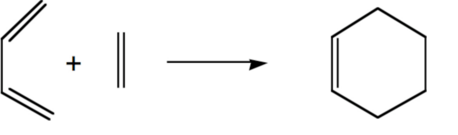
Cis-butadiene and ethylene cycloaddtion
The following concerted 4s + 2s, suprafacial cycloaddition reaction energies and structures were studied with Guassian.[6]
The Semi empirical, AM1 method was used to optimise the reactants of this reaction to begin with. Below a plot of their HOMO and LUMO are shown.
 |
 |
 |
 |
To try and compute the TS of this cycloaddition, the bond lengths of the bond forming / breaking atoms were frozen using the Redundant Coord Editor as before to a distance of ~2 Å. Afterwards a derivative was found along the reaction coordinate (the whole Hessian was not computed) because the structure created was a good enough guess for a TS to be located. The structure of the TS of this reaction is seen below:
Bond-length of the partly formed σ C-C bonds: 2.11925 Å
After a frequency calculation, this TS showed one imaginary frequency at -953.28 cm-1 was seen. This suggests that a TS has been located. An animation of this imaginary frequency is illustrated below:

The above vibration corresponds to the reaction path at the transition state, or the formation of the new bonds within the reaction. It would seem that the formation of the new bonds is synchronous. Comparing this vibration to the lowest positive frequency (at 147.24 cm-1), shown below, it would seem that the lowest frequency vibration has nothing to do with the new bond formation. This would be in line with the said frequency being positive and therefore not imaginary and so only referring to 'real' bonds that are definitely formed.
Below the HOMO and LUMO of the transition structure located are illustrated:
 |
 |
Literature values of typical sp3 C-C bond lengths are ~ 1.54 Å and for sp2 C-C bond lengths are ~ 1.46 Å and the van der Waals radius of the C atom is ~ 1.70 Å.[7] Comparing this to the C-C bond length of the partly formed σ C-C bonds in the TS of 2.11925 Å, we see that there is definitely no 'real bond' between the 2 atoms just yet. However comparing this to the van der Waals radius, the two atoms of the partially formed σ bonds are close enough for there to be some attractive interaction between them.
As mentioned briefly earlier, for the reaction to be able to take place (be allowed), phases need to match on MOs and there needs to be sufficient overlap. Comparing the cis-butadiene HOMO and the ethene LUMO it can be seen that the phases are symmetrical and form the HOMO of the TS. (Also vice versa of the reactants to form the LUMO of the TS). The reaction seems to be 'allowed' and does take place, due to efficient lowering of energy levels when reactants combine.
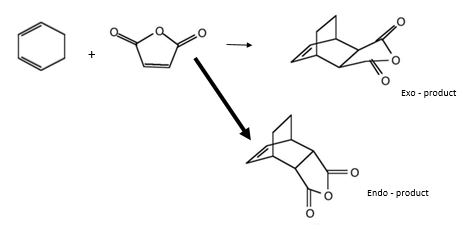
Cyclohexa-1,3-diene and maleic anhydride reaction
The following Diels-Alder reaction has substituents in both reactants which affect the preferred transition state and so product.
The HOMO / LUMO of the reactants are illustrated below:
 |
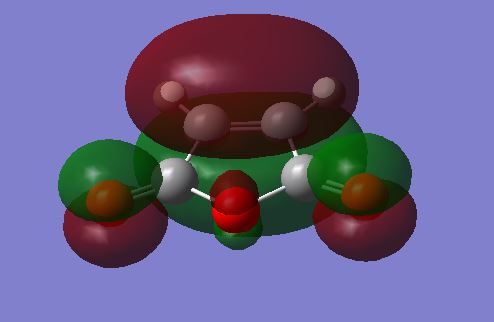 |
 |
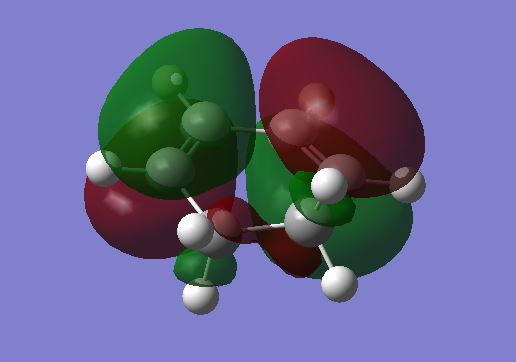 |
Locating exo product TS
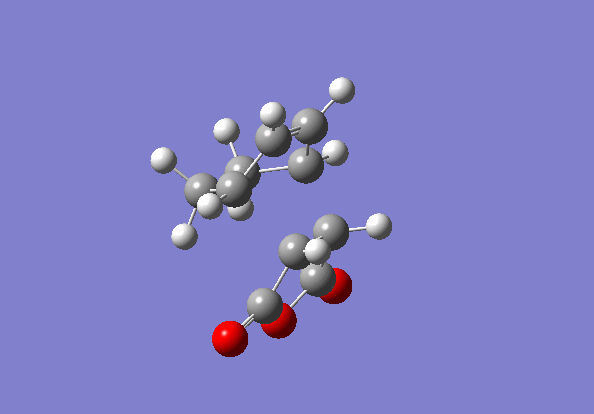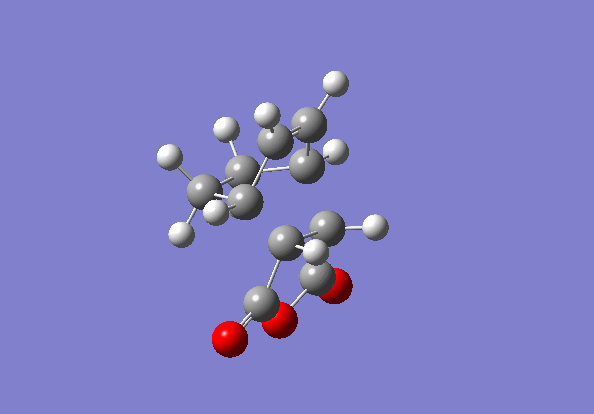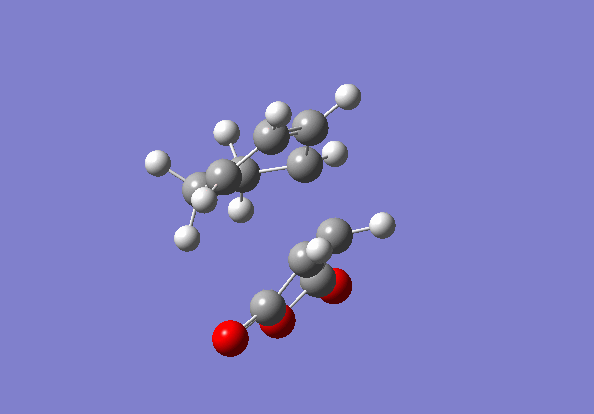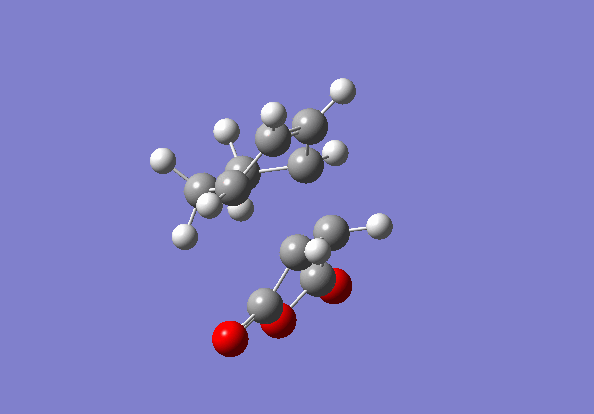
Again the transition states were located via the Semi-Empirical, AM1 level of theory. The the bond lengths of the bond forming / breaking atoms were frozen using the Redundant Coord Editor as before to a distance of ~2 Å. The bonds were then unfrozen and the TS was located as before. The structure of the TS of this reaction is seen below it is the EXO TS:
Cyclohexa-1,3-diene and maleic acid reaction TS (exo)
(Judging by the bond lengths in the above Jmol, it looks like this is the wrong TS and it doesn't match the structures below. Nonetheless it is an interesting structure. Tam10 (talk) 16:53, 12 November 2015 (UTC))
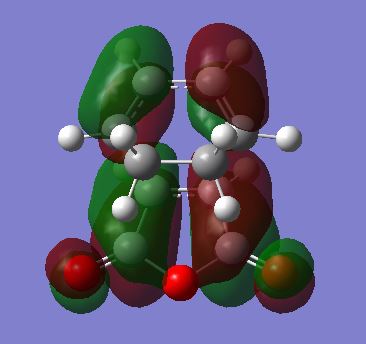 |
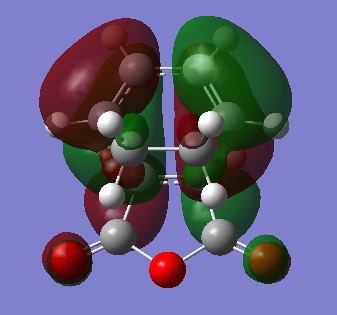 |
As before, one imaginary frequency (negative frequency) is seen suggesting a TS has been located. Frequency at -274.94 cm-1. Below is said vibration illustrated as an animation:
Locating endo product TS
Exactly the same method was applied to locate the Endo TS, just with one of reactants 'flipped' when inputting the calculations.
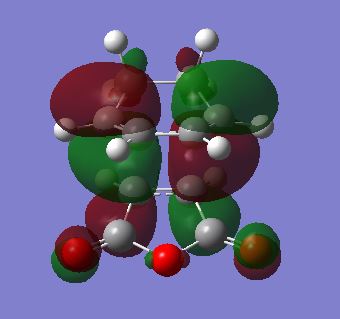 |
 |
Upon examination of the HOMO for the endo TS, the phases seem to be unmatched with the HOMO / LUMO of the reactants. It is possible that the matched orbitals that show secondary orbital interactions are not the frontier orbitals that are being looked at here. Later on the bond length examination of the endo TS compared to the reactant suggests that a reaction is very favourable. The orbitals of reactants not seeming to match to show the secondary orbital effect could be due to the level of theory used not being of high enough accuracy. (See later for limitations of the calculations in Diels-Alder reactions)
One imaginary frequency -806.41 cm-1 was seen, that gave the following vibration:
Comparisons of the TS
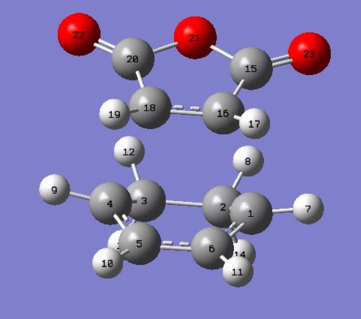
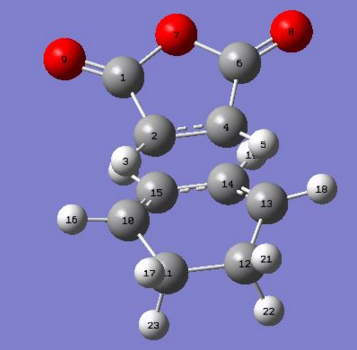
The bond lengths of reactants vs. the transition state structures were compared with the following numbering on atoms:
 |
 |
 |
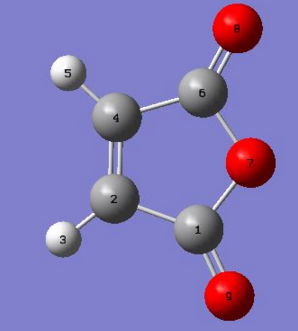 |
Bond lengths table comparing cyclohexa-1,3-diene and maleic anhydride reactants
| Cyclohexa-1,3-diene bond | Bond length / Å | Maleic anhydride bond | Bond length / Å |
|---|---|---|---|
| 6 - 5
(C-C single bond) |
1.44947 | 4 - 2
(C=C double bond) |
1.34864 |
| 5 - 4
(C=C double bond) |
1.34278 |
Bond lengths table comparing exo and endo TS structures.
| Exo TS bond | Bond length / Å | Endo TS bond | Bond length / Å |
|---|---|---|---|
| 18 - 4
( partly formed σ C-C) |
2.17701 | 2 - 10
( partly formed σ C-C) |
2.16235 |
| 5 - 6
(Beginning formation of double bond from single) |
1.39697 | 15 -14
(Beginning formation of double bond from single) |
1.39724 |
| 4 - 5
(Beginning formation of single bond from double) |
1.39439 | 15 - 10
(Beginning formation of single bond from double) |
1.39306 |
| 18 - 16
(Beginning formation of single bond from double) |
1.41129 | 2 - 4
(Beginning formation of single bond from double) |
1.40849 |
| 3 - 20
Orientation, (C-C through space distances between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the C atoms of the “opposite” -CH2-CH2- |
2.94660 | Orientation, (C-C through space distances between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the C atoms of the “opposite” -CH=CH- | 2.89222 |
With this reaction, when looking at the reactants it looks quite clear that a reaction will most likely be allowed. Since the maleic anhydride is notorious for being used as a good dienophile, where the two electron withdrawing carbonyl groups make the adjacent C atoms sufficiently electron deficient. The cyclohexa-1,3-diene is also a very good diene since it's electron rich and fixed in a trans configuration making it entropically much easier to react.
(I don't think "notorious" is the right word here! Tam10 (talk) 16:53, 12 November 2015 (UTC))
As can be seen above, the C=C double bond in maleic anhydride becomes longer in length in both TS. This shows the pi bond about to break to form into a sigma bond. Similarly comparing the C-C single bond in cyclohexa-1,3-diene that is about to become a double bond, the bond gets shorter in the two TS as it is almost a double bond but not quite the length of a double bond just yet.
If the -CH=CH- bond were not in the TS structures, then the two structures are the same in endo and exo. Measuring atom 3 and atom 20 in exo is the equivalent distance in the endo TS. In the endo TS this length (the orientation distances in table) is shorter because of the favorable secondary orbital overlap effect that must be created from the pi electrons' orbitals overlapping. The stabilising effects of the overlap have an attractive force and mean the exo TS is more strained in comparison.
Activation energies of the products
The activation energies can be calculated if we have the energies from the optimisations of the reactants and the TS, as the difference will give the activation energy. Using the DFT/B3LYP, 6-31G* method and basis set this was done with the results as follows:
| Electronic energy | Sum of electronic and thermal energies (298.15 K) | Activation energies (KCal mol-1) | |
|---|---|---|---|
| Exo TS | -612.679 | -612.49 | 18.46 |
| Endo TS | -612.683 | -612.49 | 15.85 |
| Sum of reactants | -612.71 | -612.52 |
As can be seen the endo TS leads to a lower activation energy, therefore during the reaction it is thermodynamically more favourable to form the product via the endo TS. All this is further evidence that there is a stabilising secondary orbital overlap effect with the endo TS.
Effects that might have been neglected in these calculations of Diels-Alder transition states are due to the methods and basis sets used not being of high enough accuracy. It was demonstrated in the tutorial section that the 3-21G basis set yielded less accurate C=C bond lengths than using 6-31G* basis set. The use of Semi empirical, AM1 can make many predictions that are far enough from experimental data to have a considerable effect on the accuracy of results. Examples include underestimating rotational barriers which involve double bonds and having incorrect predictions for the stability of groups.[8]
Conclusion
It has been seen that Guassian is a powerful program that is capable of locating energy minima points of molecules on their PES and these figures can be used to find reaction enthalpies and activation energies - and through this even mechanisms for reactions can be deduced.
It was seen that the use of different theory levels yielded varying results in some cases and quite similar ones in others. HF/3-21G was seen to be less accurate in predicting C=C lengths and the 6-31G* basis set was a better approximation, however this was at the price of being slower and therefore more expensive. The QST2 method was seen to be very helpful in that it was automated, but the starting points needed to be close to the desired TS or else the calculation fails.
The different conformers of the Cope rearrangement in 1,5-hexadiene were computed and two transition states located also (boat and chair). Different methods were explored to find the transition structures, the QST2 method (mentioned above) and freezing bond forming / breaking atoms were explored. Finally two Diels-Alder reactions were studied and the reaction between cis-butadiene and ethylene demonstrated how the HOMO and LUMO of the reactants overlap to form the HOMO of the TS. The reaction between cyclohexa-1,3-diene and maleic anhydride suggested the effects of secondary orbital overlap through bond lengths, but through looking at MOs it did not. This highlighted that there may be quite considerable weaknesses and limitations in the methods / theories used.
References
- ↑ O Wiest, et al., JACS., "Density Functional Theory Isotope Effects and Activation Energies for the Cope and Claisen Rearrangements" 1994, "116 (22), pp 10336-10337.DOI:10.1021/ja00101a078
- ↑ Benjamin W. Gung,* Zhaohai Zhu, and Rebecca A. Fouch, JACS., "Conformational Study of 1 ,S-Hexadiene and 1,5-Diene-3,4-diols " 1995, "117, 1783-1788.DOI:10.1021/ja00111a016
- ↑ 3.0.CO;2-X">Winter, R. F., & Rauhut, G. (2002). Computational studies on 3-aza-Cope rearrangements: protonation-induced switch of mechanism in the reaction of vinylpropargylamine. Chemistry (Weinheim an Der Bergstrasse, Germany), 8(3), 641–9. DOI|10.1002/1521-3765(20020201)8:3<641::AID-CHEM641>3.0.CO;2-X
- ↑ Lide, D. R., et al., Tetrahedron., "A survey of carbon-carbon bond lengths. Tetrahedron, 17(3-4), 125–134." 1962, "17(3-4), 125–134. DOI: 10.1016/S0040-4020(01)99012-X
- ↑ V. N. Staroverov and E. R. Davidson, J. Mol. Struct. THEOCHEM, 2001, 573, 81–89.DOI:10.1016/S0166-1280(01)00536-X
- ↑ L. Lu, S. S. Yang, Z. Wang, R. G. Cooks and M. N. Eberlin, J. Mass Spectrom., 1995, 30, 581–594.DOI:10.1002/jms.1190300409
- ↑ J.-T. Wang, C. Chen and Y. Kawazoe, Sci. Rep., 2013, 3, 3077 DOI:10.1038/srep03077
- ↑ Afarinkia, K., Bearpark, M. J., & Ndibwami, A. (2003). Computational and experimental investigation of the Diels-Alder cycloadditions of 4-chloro-2(H)-pyran-2-one. The Journal of Organic Chemistry, 68(19), 7158–66. http://doi.org/10.1021/jo0348827