Rep:JJR115 TS
Y3C Transition States and Reactivity
Introduction
This lab explored the different computational methods involved in the location and characterisation of numerous Diels-Alder reactions. The reactions explored are as follows:
- Reaction of Butadiene with Ethylene
- Reaction of Cyclohexadiene and 1,3-Dioxole
- Diels-Alder Vs Cheletropic
When locating and characterising the transition states of these larger molecules, it is no longer possible to use fitted formulae for the energy, as changes in bond type and electron distribution are not accounted for. This lab uses MO orbital based methods to determine the location of the transition sates by solving the Schrödinger equation and rationalising potential energy surfaces.
Minima and Transition States
The transition state of a reaction is defined as the critical configuration of a reaction trajectory located at the highest point of the minimal energy pathway on the corresponding potential energy surface. It is characterised as one negative Hessian eigenvalue. The term 'critical' refers to the transition state having the highest probability of completing the reaction, bridging reactants and products [1]. The location of the transition state should lead to a committer of a half, with equal probability of falling to the reactants or products in a reaction system.
Potential-energy saddle points are used to determine the location of a transition state on a potential energy diagram. The transition state is defined mathematically as a first order saddle point on a potential energy surface. All the fource constants (eigenvectors) at the transition state structure can be found by diagonalising the hessian. Saddle points have at least one negative Hessian eigenvalues. The vibrational spectrum of a transition state would be characterized by one imaginary frequency, which arises when the second derivative of the potential energy surface (force constant) is negative. This effectively means that the energy is a maximum in one direction in configurational space, and a minimal in the orthogonal direction.
Nf710 (talk) 09:27, 6 March 2018 (UTC) The eigenvalues are the force constants.
Calculating eigenvalues of the Hessian Matrix of second derivatives of the potential energy surface will identify minima, maxima and saddle points. For a general N-atom non-linear molecule with 3N-6 internal degrees of freedom, a potential energy surface can be constructed as a function of the degrees of freedom. At a minima on the PES, the second derivative can be equated to the vibrational force constant, where they are real and observable. By taking the hessian matrix eigenvalues, you can find the curvature of each dimension at a localised point. At a maximum (for example a transition state) the curvature will be negative in all degrees of freedom.
Nf710 (talk) 09:29, 6 March 2018 (UTC) Some confusion here. at a TS you will only have negative curvature in one of the dimensions. Aldo the eigen vectors are the normal modes, these are linear combinations of the degrees of freedom.
Introduction on Computational Methods
This lab involves the use of two electronic structure methods: PM6 and B3LYP. PM6 is a semi-empirical method, based on the Hartree-Fock methods, running a semi-empirical calculation using the PM6 Hamiltonian (with respect to electron position). This method is considered relatively inaccurate, as the calculation runs off of fewer integrals. This method requires knowledge of the transition state and often the wrong transition state will be found. experimental data is used to make up for the neglected integrals, and therefore many assumptions are taken, although this does make this method the fastest [2]. The average energy error for hydrogen, carbon, nitrogen and oxygen compounds is 4.6kcal/mol. In terms of bond lengths, the average error for this semi-empirical method is 0.025Å for the same elements.
The second electronic structures method used is the Density Functional theory (DFT) method; B3LYP. This method is a hybrid combination of DFT approximations while incorporating exact exchange from Hartree-Fock empirical theory. DFT improves upon Hartree-Fock calculations by including an approximation of the motions of electrons, that are only treated in an average sense in Hartree-Fock calculations [3]. The Hatree Fock calculation is used to account for the missing exchange correlation term. To this day, the B3LYP calculations are considered the most widely used theoretical tools in finding and characterizing transition states. The B3LYP method is considered much more accurate than the simplest PM6 calculations, and this experiment uses B3LYP to optimize PM6 generated geometries. (Noteː whenever a B3LYP optimisation is run in this investigation, the basis set is 6-31 and (d) has been chosen for the polarisation function).
Nf710 (talk) 09:32, 6 March 2018 (UTC) Great understanding, You could have backed up the discussion with some equations and some explanation of the basis sets.
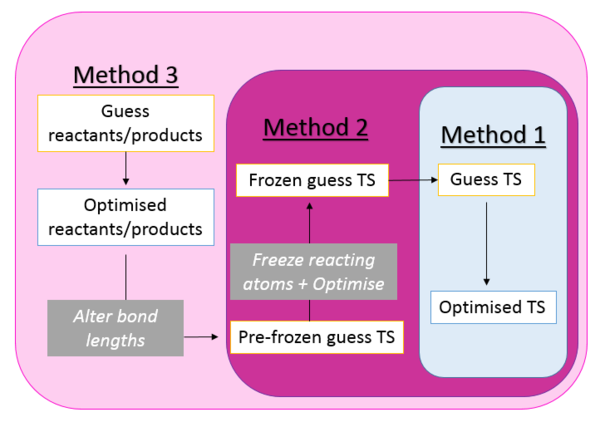
The two computation calculation methods above will be used in the following three methods for finding and characterizing transition states in the experimentː
This method runs a PM6 calculation and then a B3LYP optimization off of a 'guess' transition state. This assumes that the geometries selected are close to the transition state which is often not the case (wrong TS found, failed calculation, or multiple imaginary frequencies calculated). This method is very unreliable and therefore only used for small systems. |
This method is an extension of the first method, drawing a guess transition state structure and freezing the reacting atoms. These atoms are therefore restricted from moving and the rest of the structure is minimized to find the transition state. By freezing the atoms, the system is deemed as close as possible to the true transition state and therefore optimization more reliable. |
This method is the most reliable of the three mentioned, as it does not require exact knowledge of the transition state structure/location. Theoretically this is a longer process, with more steps involved. The method starts from either the reactants or the product structures, and bond lengths are altered and optimized (using method 2) to find the true transition state. |
The three methods used can be summarized in the following diagram (fig. 1)ː
Exercise 1
Optimization, Frequency and IRC Calculation
Exercise 1 involves the optimization of the reaction between Butadiene with Ethene, in scheme shown in figure 2. This is a thermal [4+2] cycloaddition.

Both reactants and the transition state were optimized (energetically minimised) at the PM6 level. Method 2 of optimization was used, with the terminal carbons of the butadiene and ethene being frozen (two pairs of reacting atoms). The transition state structure was first optimized to a minimum as a 'frozen guess TS', and then unfrozen and reoptimised to the transition state. A frequency calculation was run and resulted in only one negative vibration corresponding to mode 1 at 948.68i cm-1. An IRC calculation was run in both directions (TS to products, TS to reactants). The graphs produced are shown below in figure 3, with the minima and transition state structures highlighted. This was deemed a successful, asymmetric IRC with the gradient set to zero at both minima of the reactants and products and the TS. The reactants are higher energy than the products (less stable) and so it can be concluded that this is an exothermic reaction, thermally allowed pericyclic reaction.
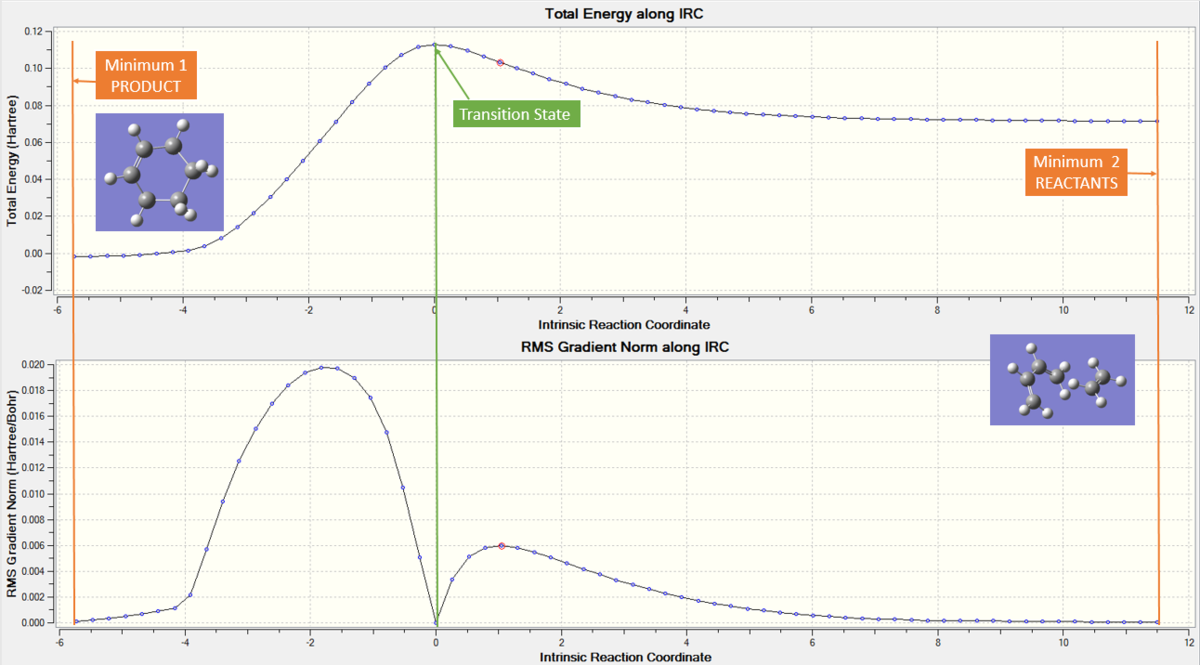
The product structure was optimized further to the same level as the other structures used in the calculation (PM6). The frequency analysis showed no negative vibrations, and therefore it can be concluded that the optimized product structure was indeed a minimum point (originally a negative vibration found, indicative of a saddle point, so the symmetry was broken and structure reoptimised to a minima).
Molecular Orbital Analysis
The MO's of the transition state were analysed when the correct TS was located and optimized, and used to construct the MO diagram below (figure 4). Jmols of the involved orbitals are displayed in the tables below. The interacting reactant MO's are also shown in the boxes either side of the MO diagram.

(Fv611 (talk) Your MO diagram is done well (as the rest of the exercise), but you have misplaced the butadiene's LUMO, which you know to have a higher energy than the TS's LUMO, as you've correctly reported their energies in the MO tables.)
In the formation of bonding and anti-bonding molecular orbitals, atomic orbitals (or in this case, fragment orbitals) have to have the correct symmetry and similar energy for a meaningful overlap. The overlapping orbitals must therefore have the same nodal symmetry for a non zero overlap, defined by the symmetry operations of the orbitals. Fragment orbitals that do not have a similar energy/equivalent symmetry partner to overlap with, will not mix and therefore will remain non bonding. This would be classed as 'forbidden' overlap. It can be seen in the MO diagram in figure four that the fragment orbitals of equivalent symmetry (asymmetric with asymmetric, and symmetric with symmetric) form strong overlaps and therefore bonding and antibonding molecular orbitals.
The overlap integral is a term quantitatively measuring the overlap of atomic (or in this case fragment) orbitals. If the symmetry of two orbitals is the same and they overlap, there will be a finite region of overlap between their orbital wavefunctions and therefore the overlap integral will be non zero (constructive interference). If the orbitals do not overlap, the combination of these orbitals does not lead to the formation of a bonding and anti-bonding pair of molecular orbitals and therefore the overlap integral will equal zero (destructive interference). The magnitude of the overlap integral will be determined by the strength of overlap, which is dependent on the similarity of the orbital energies, spacial extent of the orbitals (the type of orbital involved) and the internuclear separation. This analysis also shows that this reaction proceeds via normal electron demand, because the HOMObutadiene - LUMOethene energy gap is smaller than LUMObutadiene - HOMOethene gap. Electron demand is explained further in exercise 2.
|
|
|
|
|
| ||||||||||||
| HOMO-1 | HOMO | LUMO | LUMO+1 |
Bond Length Analysis
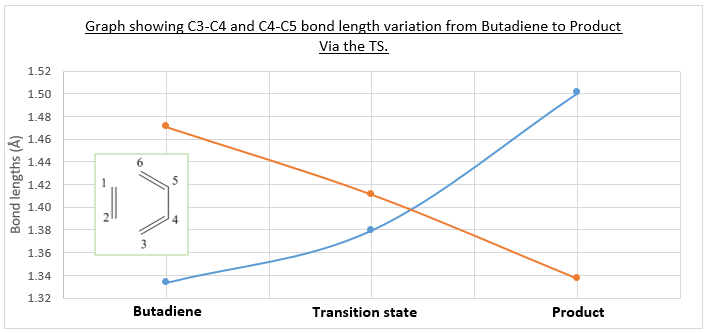
The bond lengths of the reactants, transition state and product were analysed in their optimized log files. The typical C-C Sp3 bond length is around 1.54Å, and the typical Sp2 C=C bond length is around 1.34Å. .[4]
As the table shows below (Table 1), the range of bond lengths found in the optimizations lie in between a single bond and a double bond. On the transition state, these will correspond to partially formed single/double bonds as the pericyclic reaction proceeds (concerted mechanism via a cyclic transition state).
The curve on the right (Below, right) was included to highlight the bond changing process of two important bonds in the reaction, C3-C4 and C4-C5. C3-C4 starts the reaction as a double bond, but transitions into a single bond in the product. It can be seen from the graph the the bond lengthens to from 1.33 to 1.50Å, a clear lengthening of the bond from double to single. Note, the same trend is seen for bond C5-C6 by symmetry. At the same time, bond C4-C5 transitions from a 'single' bond (1.47Å) to a shorter double bond (1.34Å). In butadiene, the bond C4-C5 is already considered partially delocalised with the rest of the pi system, hence initially shorter than the typical C-C bond lengths stated above. In both of the bonds, we observe partial bond formation at the transition state. The single bonds adjacent to the pi bond in the cyclohexene structure are also shorter because one of the carbons in the bond is sp2 hybridised with more s character (hence shorter bond than expected). The transitioning of bond types described can be observed in the negative frequency vibration of the transition state, shown in the vibrational analysis section below.
The partially formed bonds can be better understood by looking at carbon's van der Waals radius. The van der Waals radius of carbon is 1.70Å.[5]. The bonds that are partially made in the transition state are C6-C1 and C2-C3, with the transition state bond lengths being 2.1145Å and 2.1150Å respectively. These lengths are less than double the carbon van der Waals radii (3.4Å) which indicates the presence of partially formed bonds and electron cloud sharing (meaningful orbital overlap̠).
Vibration Analysis
Vib = -948.38cm-1 |
This is the only imaginary at the transition state, and corresponds to the partial formation of three single bonds (from C=C) and one double bond (from C-C). This vibration also illustrates the changes in bond length described in the section above. As the reacting atoms become closer together, the double bonds can be seen elongating, and the single bond can be seen contracting. It can also be seen that the bond making process is synchronous, with the atoms involved in bridging the two molecules together moving simultaneously. This is expected as this reaction is pericyclic, that follows a concerted mechanism by nature.
Log Files for Exercise 1
Exercise 2
This exercise involved the analysis of the reaction of Cyclohexadiene and 1,3-dioxole. This is a standard Diels-Alder cycloaddition with the production of two productsː the endo and the exo product (see figure 5 for scheme).

In order to find and analyse the transition state, method 3 was employed. This was done by optimizing the product first to the PM6 level and then to the B3LYP/6-31G(d) level. The product structure was then altered (bond lengths/angles etc) to illustrate what aspects of the molecule changes throughout the reaction. The method and results for the exo/endo mechanisms are discussed below.
Locating the Transition States
The Exo product was drawn and optimised to the PM6 and further to the B3LYP level. The bonds formed during the pericyclic reaction were broken and the two fragments were separated to be about 2.2Å from each other. This 'guess' transition state was optimized to a minimum with frozen bonds (pairs frozen were the two pairs involved in bridging the two reactants together in the final product). When both levels of optimization were achieved, the whole structure was optimized to a transition state (PM6 and B3LYP calculations ran) with force constant calculations set to 'once'. A frequency calculation was run on the final B3LYP Optimized Exo transition state, and a single imaginary frequency was found at 530.83 icm-1.
Vib = -530.83cm-1 |
The method used to find the exo transition state was repeated to find the endo transition state (see section above). The frequency analysis of the final B3LYP endo transition state found a single imaginary frequency at 520.92 icm-1.
Vib = -520.92cm-1 |
Molecular Orbital Analysis of Both Transition States
In order to understand the energetics of this reaction, an IRC was run on the system. The results of this calculation were used to understand the relative energy differences between the reactant orbitals. An energy calculation was run off of the reactants structures found in the IRC. This meant the molecular orbitals of the reactants and the transition state could be mapped, along with their relative energy positions, as seen in the molecular diagram below. Noteː this diagram could be valid (orbital orientation/overlap) for both the exo and endo transition state. This molecular orbital diagram (Fig. 6) was built from the molecular orbital diagram in exercise one, using results from the energy calculation to alter the energies of the molecular orbitals.

(Fv611 (talk) This is a very nice MO diagram, but you should have discussed the difference between endo and exo conformations in term of the relative energies of their transition states.)
|
|
|
| ||||||||||||
| HOMO-1 | HOMO | LUMO | LUMO+1 |
|
|
|
| ||||||||||||
| HOMO-1 | HOMO | LUMO | LUMO+1 |

The relative energy of the orbitals show that this reaction is under inverse electron demand. A normal electron demand reaction would involve an electron rich diene and an electron poor dienophile, as illustrated in the diagram below. The electron donating group on the diene makes it electron rich molecule with higher energy molecular orbitals. The electron withdrawing group on the dienophile decreases the energy of the molecular orbitals. In terms of the frontier MO's, this means that the HOMO of the diene (filled) will interact with the empty LUMO of the dienophile, as they are closer in energy allowing for stronger overlap .[6]. In the inverse scenario, the electron poor diene has lower energy molecular orbitals, and the electron rich dienophile has higher energy molecular orbitals. In terms of our reaction, the alpha oxygen's on the 1,3 - dioxole molecule act as electron donating groups via π donation. These donate more electron density than the alkyl groups on the diene, making the dienophile electron rich and the diene electron poor. In this situation, the strongest orbital interaction will be found between the LUMO of cyclohexadiene and the HOMO of 1,3 dioxole, as they are most similar in frontier MO energy (see figure 7). This system is different to the system explored in exercise one, where the cycloaddition was under normal electron demand. This can be seen by comparing the relative energy differences between the HOMO-LUMO of the reacting species.
The picture below (Fig 8) is a screen shot of the gaussview Molecular Orbital analysis window for the reactant species. The IRC was calculated and the initial reactant frame was used for an energy calculation (PM6 level). This snapshot confirms the explanation above, because it is clear that the HOMO is largely localized on the dienophile.

The Gaussian calculations also allowed the comparison between the endo and the exo approaches, in terms of relative transition state molecular orbital energies. Table 2 shows the relative energies of the exo and endo transition state MO's.
| Molecular Orbital | Exo Energy | Endo Energy |
| HOMO-1 | -0.19840 | -0.19648 |
| HOMO | -0.18616 | -0.19051 |
| LUMO | -0.00763 | -0.00462 |
| LUMO+1 | 0.00954 | 0.01544 |
From this it can be seen that the HOMO (and HOMO-1) of the endo transition state is lower in energy relative to the exo transition state. It would therefore be fair to say at this point that endo is the more favorable product for this reaction, because its transition state molecular orbitals are lower in energy. This is explored further in the following section.
Nf710 (talk) 09:37, 6 March 2018 (UTC) Good section. Well done for investigating the reactant MOs.
Thermochemistry and Orbital Interaction Analysis
IRC calculations were run for both the endo and exo approach to ensure the correct transition state was located. For both reactions, the product and reactant minima had gradients of zero, and an appropriate transition state was found.
With this confirmed, the thermochemistry of each system was analysed. This was done by looking at the log files (attached below) of the B3LYP/6-31(g) optimised reactant, transition state and product structures. The 'sum of electronic and thermal free energies' were tabulated and compared for the three different structures of each reaction, in order to understand the thermodynamics of the system. The result can be seen in figure 9. Note: the energies given in the log files are in Hartree units, and were converted to kJmol-1 with the conversion 1 Hartree = 2625.49 kJkJmol-1

As predicted from the relative MO energies above, the endo product is in fact the most stable product of the two. Although it is considered a more sterically hindered product (thermodynamically less stable), the endo pathway has a lower activation energy barrier and the product is also lower in energy. This can be explained by secondary orbital overlaps. The lone pairs on the oxygen atom on the 1,3 dioxole species stabilises the transition state via π overlap with the diene. I have illustrated this point in figure 10 and 11 using the HOMO molecular orbital of the endo transition state as an example. Figure 10 shows the screenshot from the optimised transition state HOMO MO, and figure 11 is a schematic to highlight the overlapping atomic orbitals. The exo product in general will be higher in energy due to steric clash with the bridging carbons in the final structure. The secondary orbital interaction does not occur in the exo transition state as the oxygen p orbitals are facing away from the diene HOMO.
 |
 |
Nf710 (talk) 09:41, 6 March 2018 (UTC) This section was well written, well done. For your figure of SOO you could have changed the iso values to get the orbitals to actually interact. You also could have added a figure to show the steric clash in the exo. But other than that this was a good section.
Log Files for exercise 2
Reactant files
- File:OPTIMISATION DIENE B3LYP ex 2 jjr115.LOG
- File:OPTIMISATION OF DIENE PM6 ex 2 jjr115.LOG
- File:OPTIMISATION OF DIOXOLE B3LYP ex 2 jjr115.LOG
- File:OPTIMISATION OF DIOXOLE PM6 ex 2 jjr115.LOG
Exo files
- File:B3LYP OPT FREQ UNFROZEN EXO STATE FOR WIKI MO PRINT JJR115 UNFROZEN TRANSITION STATE.LOG
- File:EXO FROZEN TS B3LYP OPT TO MINIMUM EX2 JJR115.LOG
- File:EXO FROZEN TS PM6 OPT TO MINIMUM EX2 JJR115.LOG
- File:EXO PRODUCT B3LYP OPT EX 2 JJR 115.LOG
- File:EXO PRODUCT PM6 OPT EX 2 JJR 115.LOG
- File:EXO TRANSITION STATE OPTIMISATION UNFROZEN PM6 EX 2 JJR115.LOG
- File:ICR ON REOPTIMISED PM6 EXO TS EX 2 JJR115.LOG
Endo files
- File:ENDO FROZEN TRANSITION STATE OPT TO MIN B3LYP JJR115.LOG
- File:ENDO FROZEN TRANSITION STATE OPT TO MIN PM6 JJR115.LOG
- File:ENDO PRODUCT B3LYP OPTIMISATION EX 2 JJR115.LOG
- File:ENDO PRODUCT PM6 OPTIMISATION EX 2 JJR115.LOG
- File:ENDO TRANSITION STATE UNFROZEN OPTIMISATION PM6 EX 2 JJR115.LOG
- File:IRC ENDO UNFROZEN TRANSITION STATE PM6 STRUCTURE TRIAL 4 EX 2 JJR115.LOG
- File:TRIAL 2 MO ENDO TRANSITION STATE UNFROZEN OPTIMISATION B3LYP EX 2 JJR115.LOG
Exercise 3
This experiment investigates the energy and mechanistic differences between Diels-Alder and Cheletropic reactions of o-Xylylene and SO2. The two possible reaction routes are shown in the scheme below (fig. 12).

In terms of the diels-alder reaction, there are two possible sites for the reaction to occur (two distinct dienes on the o-Xylylene). These are shown in the schematic diagram figure 13.
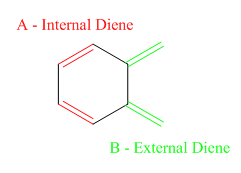
The reactions run in this part of this experiment wereː
- Endo/Exo Diels-Alder reaction at site A of o-Xylylene
- Endo/Exo Diels-Alder reaction at site B of o-Xylylene
- Cheletropic reaction at site B of o-Xylylene
The third method (mentioned in the introduction) was used to locate and analyse the five transition states involved in this reaction. For each mechanism (2 x endo/exo pairs for the Diels Alder, and a cheletropic mechanism) the product was drawn and optimised to find the minimum energy conformation. The reacting bonds were then broken, and the two 'reactant' species (that resemble the transition state) were pulled apart. The atoms involved in the reaction were then frozen, and the rest of the transition state structure was minimised to the lowest energy structure. This was all done to a PM6 level for time constraints (therefore error in the results is assumed). Finally, the transition state structure was optimised to a transition state with the calculate force constant parameter set to 'once'. IRC calculations were then completed in order to compare the energetics of each reaction, whilst also confirming that the true transition states were found. The results are shown and discussed below.
IRC Results
Noteː Click to view animation
| Exo | Endo |
|---|---|

|

|
| Exo | Endo |
|---|---|

|

|

|
The animations above show the reaction pathway from reactants to products via the transition state for all five reaction mechanisms. To understand how favorable each reaction is, the energetics were analysed in the 'thermochemistry' section in each optimized structure (reactants, products, transition state). The 'sum of electronic and thermal free energies' value for each structure allowed the following (comparative) reaction pathway to be constructed.
An interesting side note can be observed from these IRC animations. The IRC's for the endo/exo Diels-Alder reactions at the terminal diene show considerable delocalisation with the rest of the molecule before reaction with the SO2 molecule. This is the beginning of the electrocyclic reaction that can occur at the terminal alkenes, forming benzocyclobutene. The scheme is shown below (fig 14)ː

A 2000 study [7]showed that the conrotatory pathway is the lowest energy pathway, lower than the disrotatory one. The stabilisation of the aromatic product (compared to the Kekulé type reactant with alternating bonds) means this reaction occurs readily, and so xylylene is deemed unstable.
Noteː an extension would be to run these calculations, however this was not done due to time constraints.
(The delocalisation into an aromatic product is indeed the driving force (thermodynamic and kinetic) of these reactions. With an MO diagram or WH analysis, you should be able to show why it occurs via conrotation Tam10 (talk) 15:31, 5 March 2018 (UTC))
Thermochemistry Results

From the thermochemical data (fig. 15) it can be concluded that the internal diene will react much less readily than the external alkene. The activation energy for these two Diel-Alder reactions are very large compared to the other reaction routes available. Both the exo and the endo routes of this reaction mechanism are endothermic, and therefore is not enthalpically favoured. When the reaction occurs on the external diene, an aromatic ring is produced, which is largely stabilising. When the internal diene reacts, it causes an increased strain on the conformation of the molecule as a whole, and the aromaticity is disrupted (the alkenes are less conjugated than the starting material).
When looking at the reactions occuring at Diene B (terminal alkene) it can be sen that although the cheletropic transition state is considerably higher in energy than the diels-alder reactions (larger activation energy), the product is in fact the most stable of the three. This is due to the fact that the strong S=O bond is not broken in the reaction. In terms of the two diels-alder reactions, the exo product is the thermodynamic product, whereas the endo is the kinetic product (will occur faster due to a lower energy transition state. This can be explained by secondary orbital interactions, with the external S=O bond tucked in closer to the rest of the molecule, allowing for some orbital overlap that reduces the energy of the transition state intermediate.
Log Files Exercise 3
Diels-Alder at Site A
- File:SITE A ENDO FROZEN TS PM6 TO MINIMUM EX 3 JJR115.LOG
- File:SITE A ENDO IRC CALC TS PM6 EX 3 JJR115.LOG
- File:SITE A ENDO PRODUCT OPTIMISATION PM6 EX 3 JJR115.LOG
- File:SITE A ENDO UNFROZEN TS PM6 TO TS EX 3 JJR115.LOG
- File:SITE A EXO FROZEN TO MIN PM6 EX 3 JJR115.LOG
- File:SITE A EXO IRC CALC (FROM REDO) PM6 EX3 JJR115.LOG
- File:SITE A EXO PRODUCT PM6 OPTIMISATION EX 3 JJR115.LOG
- File:SITE A EXO UNFROZEN TO TS PM6 EX 3 JJR115.LOG
Diels Alder at Site B
- File:SITE B ENDO FROZEN TS PM6 TO MIN EX 3 JJR115.LOG
- File:SITE B ENDO IRC TRANSITION STATE CALC EX 3 JJR115.LOG
- File:SITE B ENDO PRODUCT OPTIMISATION PM6 EX 3 JJR115.LOG
- File:SITE B ENDO UNFROZEN TS PM6 TO TS EX 3 JJR115.LOG
- File:SITE B EXO FROZEN TS TO MIN PM6 OPTIMISATION EX 3 JJR115.LOG
- File:SITE B EXO IRC TS PM6 CALC EX 3 JJR115.LOG
- File:SITE B EXO PRODUCT PM6 OPTIMISATION EX 3 JJR115.LOG
- File:SITE B EXO UNFROZEN TS PM6 OPTIMISATION EX 3 JJR115.LOG
Cheletropics
- File:CHELOTROPIC FROZEN TRANSITION STATE PM6 OPTIMISATION EX 3 JJR115.LOG
- File:CHELOTROPIC PRODUCT PM6 OPTIMISATION EX 3 JJR115.LOG
- File:CHELOTROPIC TRANSITION STATE IRC CALCULATION EX 3 JJR115.LOG
- File:CHELOTROPIC UNFROZEN TRANSITION STATE PM6 OPTIMISATION EX 3 JJR115.LOG
Extension
This extension explores the unexpected stereochemistry for the ring opening of this cyclobutene structure with ester groups orientated in the way shown in the scheme below (figure 16). This is an interesting investigation as the unusual outcome is one of three other viable options, and is dictated by electronics of the system.
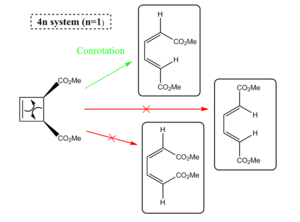
This is a 4π electrocyclic reaction, which is thermally allowed. The equilibrium will exist largely on the right of the system towards the more strain free molecule structure. As a 4n πe reaction, under thermal conditions this will occur with conrotatory motion, but will occur with disrotatory motion of the orbitals under photochemical conditions. This follows Woodward-Hoffman rules for electrocyclic reactions. During the interconversion of the cyclobutene to butadiene (ring opening) the C2 symmetry axis is retained in the reaction under conrotatory motion. However photochemically, this two fold axis of symmetry is not retained and instead the mirror plane is retained from reactants to products, which can be seen in the scheme.
Figure 17 - is a simple diagram from source ([8]) that highlights the change in orbitals throughout the ring opening process.

(You should show these MOs so the reader knows what you mean.
IRC Results
From the animation above, the conrotatory motion of the two ester groups can be seen, as they both move in an anticlockwise direction, resulting in an asymmetric end product (one of the alkenes having E stereochemistry, and the other having Z).
| Activation Energy kJ for Conrotatory /mol | Reaction Energy for Conrotatory kJ/mol |
| 163.7 | -53.9 |
Log Files for Extension
- File:EXTENSION B3LYP OPTIMISATION OF reactant JJR115.LOG
- File:EXTENSION IRC CALC ON TRANSITION STATE PM6 JJR115.LOG
- File:EXTENSION OPT TO A MINIMUM FROZEN TRANSITION STATE JJR115.LOG
- File:EXTENSION PM6 OPTIMISATION OF PRODUCT JJR115 CORRECT.LOG
- File:EXTENSION PM6 OPTIMISATION OF reactant JJR115.LOG
- File:TRIAL 4 EXTENSION OPTIMISATION TO A MINIMUM FROZEN TRANSITION STATE JJR115.LOG
Conclusion
To conclude, the PM6 and B3LYP methods of optimization and location of transition state were able to reasonably map the reaction pathways of the various experiments above. In exercise one, the molecular orbital analysis and IRC calculations confirmed the correct transition state was found via the computational methods used. In exercise two we were able to observe secondary orbital interactions via the molecular orbital analysis calculations in the optimised product to explain why the endo product was the most favourable. In exercise three, the cheletropic product was deemed the most thermodynamically favourable, whereas the terminal diels-alder mechanism (endo approach) was found to be the kinetic product with a lower energy barrier.
Although the PM6 calculation involves a considerable amount of doubt and error (many broad assumptions made in the calculation), combined with the more advanced B3LYP calculation, this experiment yielded good results that correlates with literature data found.
References
- ↑ T. Fueno, The Transition State, CRC Press, 1999, p2.
- ↑ J. J. P. Stewart, J. Mol. Model 13, 1173-1123 (2007).
- ↑ D. J, Singh, L. Nordstrom, Planewaves, Pseudopotentials and the LAPW method, 2006, p6-21.
- ↑ P. Dewick, Essentials of Organic Chemistry, John Wiley & Sons, 2013, p44
- ↑ S. Batsanov, Van der Waals Radii of Elements, Inorganic Materials, Vol. 37, No.9, 2001
- ↑ J. Clayden,S. Warren, N. Greeves, Organic Chemistry [e-book]. Oxford: OUP Oxford; 2012, ch. 34, p886-888
- ↑ 7.0 7.1 S. Sakai, Theoretical Studies of the Electrocyclic Reaction Mechanisms of o-Xylylene to Benzocyclobutene, J. Phys. Chem. A 2000, 104, p11615-11621
- ↑ 8.0 8.1 B. Dinda, Essentials of Pericyclic and Photochemical Reactions, Lecture Notes in Chemistry 93, Springer INternational Publishing Switzerland 2017, DOI 10.1007/978-3-319-45934-9_2