Rep:JHT114 Y3C TransitionStates fw
JHT Y3C Transition States Further Work
Introduction
Both the 4π electrocyclic and 6π electrocyclic ring-closing reactions were investigated at the PM6 level. The reaction coordinates of these reactions were visualised, and an MO analysis was done on the 4π electrocyclic system.

4π Electrocyclic
Optimisation of Structures (PM6 Level)
| Table 1: Optimised Structures at PM6 Level | ||||||||
|---|---|---|---|---|---|---|---|---|
| Reactant | Transition State | Product | ||||||
Visualisation of Reaction Coordinate
| Reaction Coordinate | 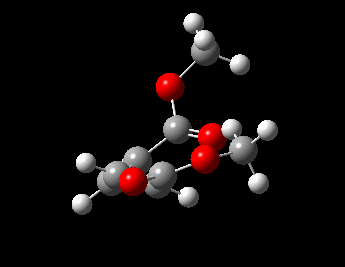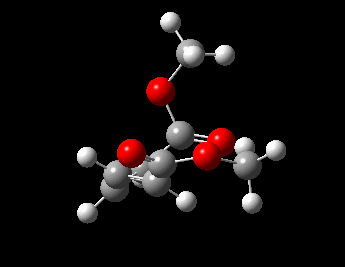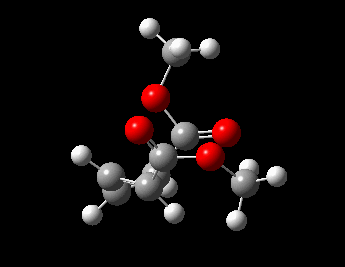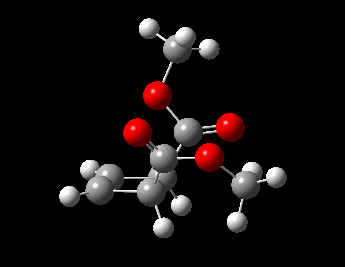
|
|---|---|
| IRC Calculation | 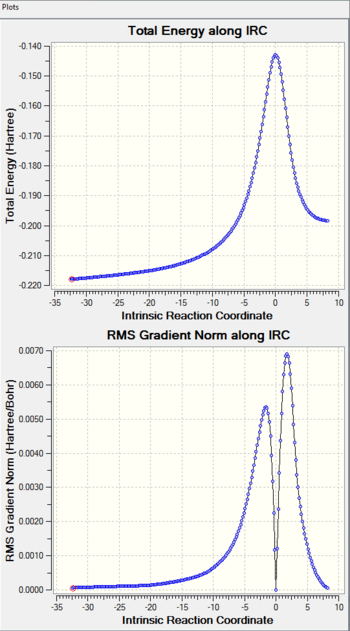
|
| IRC File | File:Jht 4PI IRC fw.LOG |
(A bit difficult to see the reaction from this angle Tam10 (talk) 16:03, 19 February 2018 (UTC))
Molecular Orbitals and Analysis
| 1,3-Butadiene Fragment | Molecular Orbital Diagram | Cyclobutene TS | ||||
|---|---|---|---|---|---|---|
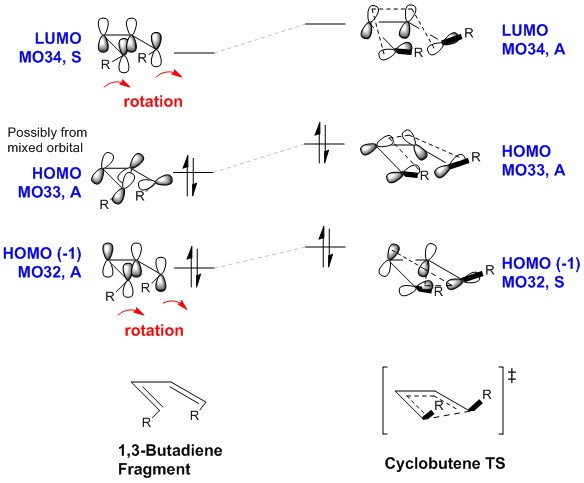
|
||||||
| LUMO, MO34, S | LUMO, MO34, A | |||||
| HOMO, MO33, A | HOMO, MO33, A | |||||
| HOMO(-1), MO32, A | HOMO(-1), MO32, S |
For a typical 4 π system, the HOMO should resemble that of HOMO(-1), MO32, A
of the diene fragment, which could be predicted using Huckel theory. However, the HOMO, MO32, A
does not resemble this. Thus, it could be possible that MO32 is formed as a result of mixing of with the ester groups, which are in conjugation with the double bond.
Nonetheless, from MO32 and MO34 , it can be noted that the reaction is conrotatory . This is in accordance to a thermal reaction governed by the Woodward-Hoffmann rules:
(The orbitals aren't too easy to understand in this example. There also might be some swapping going on in the orbitals Tam10 (talk) 16:03, 19 February 2018 (UTC))
4ra = 1 (4n+2)s = 0 sum = 1 (odd number)
6π Electrocyclic
Optimisation of Structures (PM6 Level)
| Table 2: Optimised Structures of 6п electrocyclic reaction at PM6 Level | ||||||||
|---|---|---|---|---|---|---|---|---|
| Reactant | Transition State | Product | ||||||
Visualisation of Reaction Coordinate
| Reaction Coordinate | 
|
|---|---|
| IRC Calculation | 
|
| IRC File | File:JHT 6PI IRC fw.LOG |
In contrast to the 4π system, the 6π system shows a disrotatory
behaviour, as can be seen from the gif file in the reaction coordinate above. This is in accordance to the Woodward-Hoffman rules under thermal conditions:
4ra = 0 (4n+2)s = 1 sum = 1 (odd number)
(Good. This can also be reinforced with orbital analysis Tam10 (talk) 16:03, 19 February 2018 (UTC))
Conclusion
Both calculations are in accordance to the Woodward-Hoffman analysis, where a 4π electrocyclic reaction would proceed in a conrotatory manner, which allows for antarafacial interactions; whereas a 6π electrocyclic reaction would proceed in a disrotatory manner, allowing suprafacial interactions.
Exercises 1, 2 and 3
Links to previous exercises:
Exercise 1: https://wiki.ch.ic.ac.uk/wiki/index.php?title=JHT114_Y3C_TransitionStates
Exercise 2: https://wiki.ch.ic.ac.uk/wiki/index.php?title=JHT114_Y3C_TransitionStates_ex2
Exercise 3: https://wiki.ch.ic.ac.uk/wiki/index.php?title=JHT114_Y3C_TransitionStates_ex3
