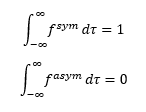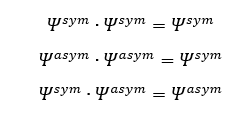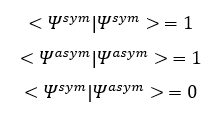Rep:JHT114 Y3C TransitionStates

Introduction

Importance and Basic Principles of Computational Chemistry

The high accuracy and ease of accessibility of computational chemistry, brought about by numerous incremental advancements, makes it an important tool for understanding many chemical behaviours. The complementary nature of computational and experimental chemistry provides both the theoretical framework and evidence of a proposed hypothesis, making neither approach sufficient on its own.

Since chemical reactivity is rationalised through electron motion, the heart of computational chemistry lies in solving the time-independent Schrödinger equation (1) for E and Ψ:

Ĥ Ψ = E Ψ (1)

where the Hamiltonian Ĥ is given by Ĥ = T_n+T_e + V_ee+V_en+V_nn. From the Born-Oppenheimer approximation, T_n=0, and V_nn is a constant Coulombic potential. From the 3^rd postulate of quantum mechanics, the other terms can be obtained from their corresponding classical expressions.

The wavefunction Ψ is an asymmetric function which can be written as a Slater determinant, specified by spin orbitals. These orbitals are approximated using the Linear Combination of Atomic Orbitals, where the basis set determines the accuracy of a calculation at the cost of computational power. Usually, Gaussian-type orbitals are used instead of Slater-type orbitals due to computational efficiency, since Slater orbitals have a discontinuous gradient.

Since the wavefunction for many-electron systems cannot be solved exactly, various methods have been developed to obtain approximates to the true wavefunction in the Schrödinger equation. The approximate solutions to the electronic part of the Schrödinger equation gives information about Molecular Orbitals, whereas that of the nuclear part gives information about vibrations. Examples of computational methods used include the Hartree-Fock method, molecular mechanics, density functional theory (DFT) and semi-empirical methods. In this exercise, the semi-empirical method (PM6) and DFT method (B3LYP) were employed to investigate chemical reactivity.

Briefly, the Semi-empirical Parameterization Method 6 (PM6) improves computational efficiency by making approximations such as Neglect of Diatomic Differential Overlap (NDDO), where some integrals that give electron density are simplified and neglected. For kept integrals, the efficiency is further improved through semi-empirical nature of this method, where some parameters are calculated from experimental values.

In the DFT method, electron density is treated as a function of cartesian coordinates. The energy of a system is then treated as a function of electron density.

 Electron Density = ρ(x,y,z)
 Energy           = E(ρ(x,yz))

The B3LYP method solves for the function of E by employing various approximations such as the Local Density Approximation (LDA), Hartree-Fock approximation, Becke-1988 (B88), Lee-Yang-Parr 1988 (LYP88), and Vosko,Wilks, Nusair 1980 (VWN80).

Nf710 (talk) 23:38, 22 February 2018 (UTC) This is an excellent section you have clear done some exxtra reading about understood why we need all these different methods. B3LYP uses the DFT hamiltonian but just the HF and LDA etc in the exchange correlation term and is hence known as a hybrid.

Potential Energy Surfaces and Stationary Points

Through the methods above, a potential energy surface of the system investigated is generated. Since the force acting on an object with potential energy E(r) is given by:

F = -dE(r)/dr

If a particle is in equilibrium, there is no net force acting on it. Translating this to a potential energy diagram, this corresponds to a stationary point of 0 gradient. Displacing the system would result in a net force (in the opposite direction) that restores the it to a minimum point. However, both minima and transition states are located at stationary points. Hence, computing the first derivative alone would be insufficient to distinguish between the two states.

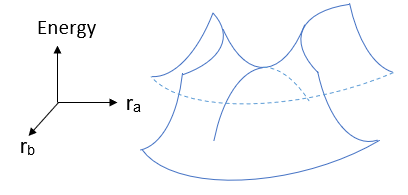
With a one dimensional reaction coordinate, the transition state corresponds to a maximum point, where the second derivative is negative; whereas a minima corresponds to a point where the second derivative is positive. However, most reactions, if not all, involve degrees of freedom >1. An example with 2 degrees of freedom is shown:

The transition state now has a positive second derivative in the r_a direction, and a negative second derivative in the r_b direction. Generalising this to a system with N atoms, with 3N-6 degrees of freedom (3N-5 for linear systems), a minima and a transition state is characterised by:

	Minima	Transition State
dE(r)/dri	0 for all i	0 for all i
d2E(r)/dri2	positive for all i	negative for 1 i, positive for all other i

Note: stationary points with more than 1 negative second derivative are not chemically significant since there will be an alternative pathway of lower energy.

Since stationary points can correspond to either a minima or a transition state, the second derivative is computed to distinguish between them. In a simple harmonic oscillator, the second derivative gives the force constant, which can then be translated into a vibration frequency. Thus, a minima should only show positive vibration frequencies, whereas a transition state should give one imaginary frequency, represented by a negative number in Gaussian.

Nf710 (talk) 23:43, 22 February 2018 (UTC) At the TS you daigonalise the hessian matrix in the basis of the degrees of freedom. your eigenvalues are the force constants and their corresponding eigenvectors are the normal modes which are linear combinations of the degreees of freedom. That when when you move along this eigenvector as a vibration it looks like a bond forming movoment as all degrees of freedom are moving at the same time.

Thermodynamics and Kinetics

Once the lowest energy pathway is determined, the reaction energy and activation barrier can be obtained from the difference in energies of the stationary points. However, these are energies at absolute 0 for an isolated molecule. To enable meaningful data to be extracted, statistical thermodynamics is employed, which allows for the determination and prediction of chemically interesting properties such as the molecular geometry and spectroscopic data at room temperature.

Exercise 1

(Fv611 (talk) Very good discussion throughout, only hiccup is the ordering of your MOs in the diagram.)

Scheme 1: Diels-Alder Reaction between Butadiene and Ethene

The Diels-Alder reaction between Butadiene and Ethene was investigated at the PM6 Level. A retrosynthetic-like approach was adopted, where the structures of the products were first optimised. Thereafter, the bonds that were formed during the course of the reaction were 'broken' in Gaussian. The C-C bonds that were broken were set to 2.2 Å, between the length of a C-C single bond and 2x the Van der Waal's radii of carbon. This structure was first optimised to a minimum, and then optimised to a Berry Transition State. A frequency analysis was carried out to confirm that the structure was a transition state. (only 1 negative frequency) To further confirm that the TS structure obtained was valid, an Intrinsic Reaction Coordinate (IRC) was calculated, where the reactants, transition structure and product showed gradients of 0.

Further analysis on the interactions of molecular orbitals of the reactants were also carried out to determine the symmetry allowed and disallowed interactions. C-C bond distances were also measured for the progress of the reaction, which would give an indication of whether the reaction is synchronous or asynchronous.

Optimised Structures

Table 1: Optimised Strcutures at PM6 Level
Ethene	1,3-Butadiene	Transition State	Cyclohexene

Frequency Calculation and IRC of Transition State

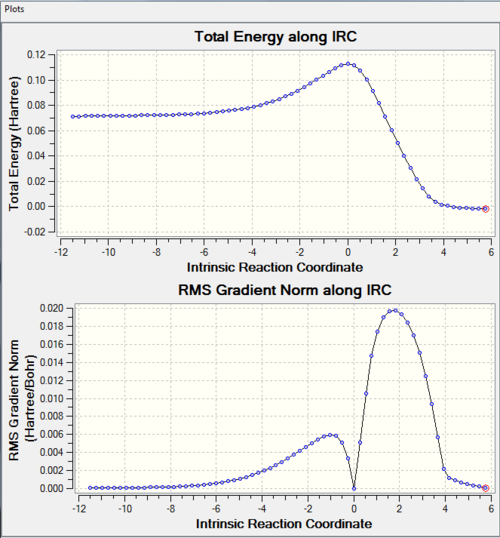
Only 1 'negative' vibration frequency, which corresponds to the direction reaction coordinate. The IRC is shown in Table 2 below:

Table 2: Intrinsic Reaction Coordinate at PM6 level
Reaction Coordinate	Energy Level vs Reaction Coordinate	Explanation
		The reactants, transition state and product correspond to stationary points. Hence, reaction coordinates corresponding to these structures (reactants= -11.5, TS= 0.0 and products= 6) have RMS gradients of 0. As expected, the IRC shows the shape of a typical potential energy diagram for the progress of a reaction. This is in accordance with the fact the IRC is calculated along specific path of the multi-dimensional potential energy surface in Gaussian. In this reaction coordinate, the reaction is exothermic.
File:Jht TS PM6 IRC ex1.LOG

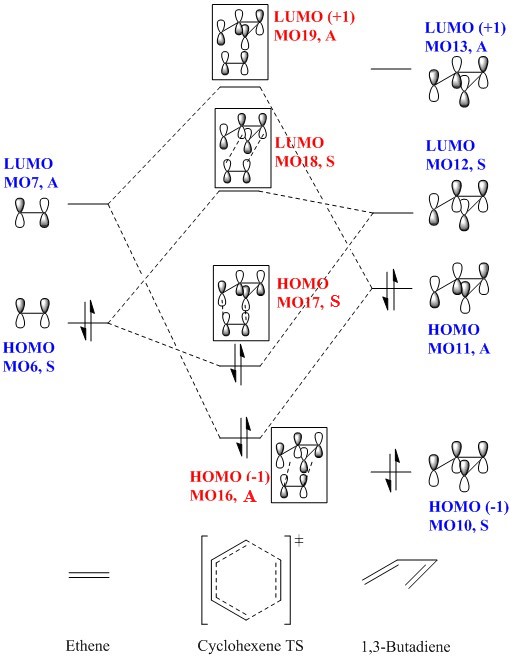
Molecular Orbital Diagram and Analysis

(Fv611 (talk) You didn't consider the energy of your computed TS MO diagrams, which is a shame - for example, your TS log file gives an energy for your TS HOMO-1 of -0.32 a.u., and for your ethene HOMO of -0.35 a.u, but you draw the ethene HOMO as higher in energy.)

Ethene	Molecular Orbital Diagram	1,3-Butadiene
LUMO, MO7, A		LUMO, MO12, S
HOMO, MO6, S		HOMO, MO11, A

Transition State	Frontier Orbitals
	TS HOMO(-1), MO16, A	TS HOMO, MO17, S	TS LUMO, MO18, S	TS LUMO(+1), MO19, A

The overlap integral is given by <Ψ_a|Ψ_a>

For normalised functions,

Since

The overlap integral for symmetric-asymmetric, symmetric-symmetric and asymmetric-asymmetric functions are

From this, it can be concluded that only orbitals of the same symmetry interact. Otherwise, the overlap integral would be 0. This is consistent with the MO diagram and calculated molecular orbitals above, where only orbitals of the same symmetry interact, giving a transition state MO of the same symmetry.

Although LUMO(+1), MO13 of 1,3-butadiene has the same symmetry as LUMO, MO7 of ethene, these do not interact. This is possibly due to the closer energy of butadiene HOMO, MO11 to the LUMO of ethene, making them interact more strongly. Also, interactions of filled-unfilled orbitals are preferred over interactions of unfilled-unfilled orbitals.

Thus, the interactions which give rise to the TS molecular orbitals are

   TS HOMO(-1), MO16, A = Ethene LUMO, MO7, A + Butadiene HOMO, MO11, A
   TS HOMO, MO17, S     = Ethene HOMO, MO6, S + Butadiene LUMO, MO12, S 

   TS LUMO, MO18, S     = Ethene HOMO, MO6, S - Butadiene LUMO, MO12, S
   TS LUMO(+1), MO19, A = Ethene LUMO, MO7, A - Butadiene HOMO, MO11, A

Symmetry Allowed Reactions

The above has led to the formulation of the Woodward-Hoffman rules. Allowed reactions are summarised as:

Thermally Allowed	Photochemically Allowed
(4n+2)s + (4r)a = odd number	(4n+2)s + (4r)a = even number

where s and a denotes suprafacial and antarafacial, n denotes the number of π electrons in the suprafacial component, and r denotes the number of of π electrons in the antarafacial component.

In this thermal [4+2] cycloaddition reaction,

   (4n+2)s = 1 (ethene) 
   (4r)a = 0
   sum = 1

Hence, it is thermally allowed provided that the components interact in a suprafacial manner.

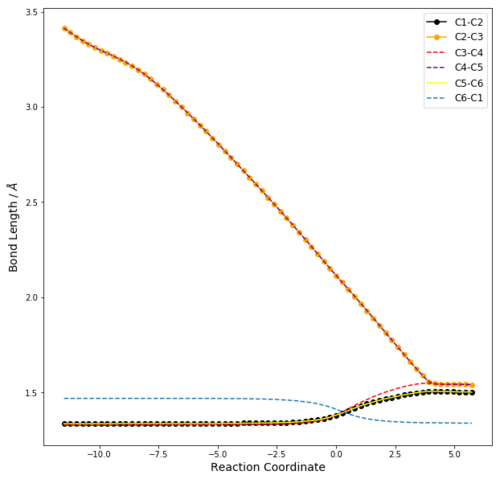
C-C Bond Length Analysis

Table 3: Change in C-C Bond Lengths with Reaction Coordinate
Vibration Corresponding to Reaction Coordinate	Change in C-C bond distance

Table 4: C-C Bond distances (Labels used correspond to that used in Table 3)
	C-C bond distance (Å)
Atom Label	Ethene	1,3-butadiene	TS	Cyclohexene
C1-C2		1.33344	1.37974	1.50084
C2-C3			2.11483	1.53717
C3-C4	1.32731		1.38173	1.53462
C4-C5			2.11444	1.53716
C5-C6		1.33344	1.37976	1.50082
C6-C1		1.47069	1.41114	1.33695

Table 5: Typical C-C bond distances
C-C bond type	Bond distance / Å
2x VdW radii of C	3.4
sp3-sp3 C-C	1.50-1.54
sp2-sp3 C-C	1.49
sp2-sp2 C=C	1.34 [8]
sp2-sp2 partial C=C (benzene)	1.397 [8]
sp2-sp2 partial C=C (graphite)	1.421 [8]

In comparison to that of typical C-C bond lengths, the C=C lengths in ethene and butadiene corresponds to typical double bonds. However, the C-C single bond in butadiene is slightly shorter than typical sp²-sp³ C-C single bonds. This can be explained by conjugation of the double bond, which can be seen in MO10 of butadiene. Both C-C and C=C in cyclohexene correspond to that of typical bond lengths.

From the change in bond lengths shown in the IRC, the changes in bond type can be summarised as:

Atom Label	Change in bond order
C1-C2	2 to 1
C2-C3	0 to 1
C3-C4	2 to 1
C4-C5	0 to 1
C5-C6	2 to 1
C6-C1	1 to 2

In the transition state, the bond length between C2-C3 and C4-C5 is significantly shorter than 2x the Van der Waal's radius carbon, but longer than that of a typical single bond length. The bond lengths of C1-C2, C3-C4 and C5-C6 are similar to that of benzene, whereas that of C1-C6 is similar to that of graphite. This can be rationalised by the formation of partial double bonds between the described atoms in the transition state, since the bonds involved undergo a change in bond order from 2 to 1 or 1 to 2.

From the vibration corresponding to the reaction path, the formation of the two bonds is synchronous, since C2-C3 and C4-C5 move towards/away from each other at the same rate. This is further supported by the simultaneous change in bond distances with reaction coordinate between C2-C3 and C4-C5 in Table 3, where the plots corresponding to these two bond distances are seen to overlap.

Exercises 2, 3 and Further Work

Due to the wiki page becoming slower to load due to the number of Jmol objects, Exercises 2, 3 and Further work are available at:

Exercise 2: https://wiki.ch.ic.ac.uk/wiki/index.php?title=JHT114_Y3C_TransitionStates_ex2

Exercise 3: https://wiki.ch.ic.ac.uk/wiki/index.php?title=JHT114_Y3C_TransitionStates_ex3

Further Work: https://wiki.ch.ic.ac.uk/wiki/index.php?title=JHT114_Y3C_TransitionStates_fw