Rep:Hrc115ts

Introduction

Transition States

A transition state is the point in a reaction pathway with the highest energy. It is this energy barrier that the reactants must be able to overcome for a reaction to complete, due to factors such as steric hindrance and orbital overlaps. It has no bearing on the stability of the product (when more than one product can result from a reaction) which is determined by its own set of factors. These differences are shown in figure 1.

Figure 1ː Reaction barrier and energy

In order to be able to determine the geometry of the transition state, the reaction must be considered across a potential energy surface. The transition state is found at a first-order saddle point, and using known electron structures, the geometry can be determined.

Nf710 (talk) 11:37, 9 February 2018 (UTC) You needed to mention here that the PES is in 3N-6 degrees of freedom and that a minium has a positive second derivative in all dimensions and a zero first. and a TS has a 0 first derivative also band positive 2nd derivatives in all teh dimensions except one which is negative and this is the reaction coordinate. these force constants (2nd derivatives) can be found by diagionalising the hessian matrix

Computational Methods

Gaussview was used for all calculations. The reactants, products, and transition states were optimised (from their drawn configurations on Gaussview to their true structures) by using a PM6 (semi-empirical) method. However, this makes a lot of approximations, uses parameters taken from data, and omits some factors entirely. A second method used is the B3LYP (density functional theory) method. This does not make as many approximations and is far more accurate. However these take a long time, so molecules were always first optimised via the PM6 method.

Nf710 (talk) 11:37, 9 February 2018 (UTC) Nice initial understanding, some equations would have complemented your discussion here.

To find the transition states in exercises one and two, a guess transition state was made, optimised to a minimum, and then optimised to a transition state. In the third exercise, first the products were made, bonds were broken, and then optimised to a transition state.

Exercise 1ː Reaction of Butadiene with Ethylene

(Fv611 (talk) Very nice section overall. Well done!)

Molecular Orbitals

The reaction between ethylene and butadiəne is a [4+2] cycloaddition, shown in figure 2.

Figure 2: Reaction between butadiene and ethylene.

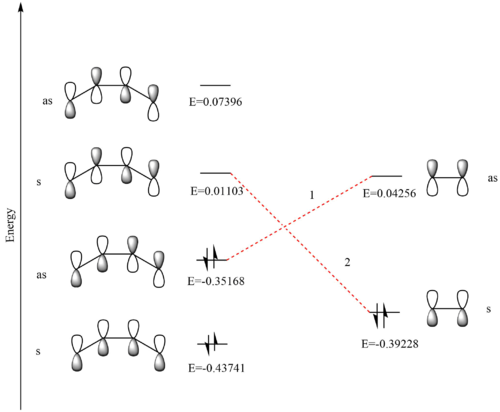
Figure 3 shows an MO diagram for the two reactant including the HOMO and LUMO on each. The energies (in au.) for each set of orbitals have been calculated in Gaussview. The labels of 's' and 'as' correlate to symmetric or anti-symmetric orbitals respectively.

Figure 3ː Molecular orbital diagram of butadiene (left) and ethylene (right).

The HOMOs and LUMOs on each molecule shown in figure 3 have been visualised in gaussview and are shown in figure 4.

Figure 4ː Butadiene and ethylene molecular orbitals

Butadiene HOMO	Butadiene LUMO	Ethylene HOMO	Ethylene LUMO

There are two HOMO-LUMO interactions shown as 1 and 2 in figure 3. It can be seen that the symmetric HOMO interacts with the symmetric LUMO, and this also holds true for the anti-symmetric orbitals. From this it is possible to draw the conclusion that interacting orbitals must be of the same symmetry for a reaction to be allowed, otherwise it would be forbidden. The orbital overlap integral would then have a value of zero for symmetric - anti-symmetric interactions (meaning that there are no orbitals overlapping) and non-zero for a symmetric - symmetric or anti-symmetric - anti-symmetric overlap (corresponding to some degree of overlap). These four orbitals on the reactants make four new orbitals in the transition state, a new HOMO and LUMO, one with an energy lower than the HOMO (HOMO - 1), and one with an energy higher than the LUMO (LUMO + 1). An observation of the new orbitals formed in Gaussview reveals that interaction 2 leads to the new HOMO and LUMO, and 1 creates the orbitals on either side of these. This can also be seen from the energy differences between the orbitals, as the combination with the smaller difference leads to the new HOMO and LUMO. Interaction 1 has an energy difference of 0.40331 au, and 2 of 0.39424 au. These new molecular orbitals are shown in figure 5, and the transition state molecular orbital diagram is shown in figure 6.

Figure 5ː Transition state molecular orbitals

HOMO-1	HOMO	LUMO	Lumo + 1

Figure 6ː MO TS diagram for reaction between butadiene and ethylene.

In figure 6 it shows that the new HOMO is higher in energy than the ethylene HOMO from which it is partly comprised. This is because it is the MO diagram of a transition state, which is the highest energy point in the reaction pathway. This is the activation energy which must be overcome to reach the products.

Bond Lengths

Figure 7 shows the changes in bond lengths that occur throughout the reaction. Lengths are given in Angstroms. The typical sp3 and sp2 bond lengths are 1.54 A and 1.34 A respectively, and the van der Waal's radius- half of the smallest possible length between two non-bonded atoms- is 1.70 A.

Figure 7ː Changes in bond lengths throughout the reaction

Upon going from the reactants to the transition state, the double bonds lengthen and single shortens. As the reaction then proceeds to the products, the new double bond mirrors the length of those found in the products. The single bonds are all longer than that one seen in the butadiene, with those adjacent to the new double bond slightly shorter than the others. This is due to the product having an overall less sp2 character than the reactants. In the transition state, all the bond lengths exist between the lengths of those of typical sp3 and sp2 carbon-carbon bonds- the transition state shows an intermediate where the bonds exist as though between states and is not a stable product. The distance between carbons 1 & 6, and 4 & 5, which will become bonded in the product, are observed to be 2.11 A. This is longer than the van der Waal's radius (1.70 A), showing that the atoms are still far apart enough to not need to be bonded. This also helps to prove the structure found is indeed the transition state as the 6 -membered ring is yet to be formed.

(Fv611 (talk) The Van der Waal's distance between the two carbon atoms is actually double the carbon's van der Waals radius.)

TS Vibration

When the imaginary vibration of the transition state is animated, the movement corresponding to the reaction pathway at this point can be seen, as shown in figure 8.

Figure 8ː Transition State Vibration

The distance between the two pairs of terminal atoms reduces at the same rate. This shows that the reaction proceeds via a concerted mechanism, where all new bonds are formed at the same time.

Log Files

File:HRC115 DAPROD3.LOG - optimised product

Exercise 2ː The reaction of cyclohexadiene with 1,3-dioxole

Molecular Orbitals

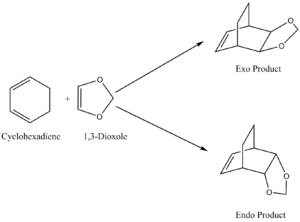
The reaction between cyclohexadiene and 1,3-dioxole is also a [4+2] cycloaddition. However in this case, two different stereoisomers may be synthesised; an endo or an exo product. This is shown in figure 9.

Figure 9: Reaction between cyclohexadiene and 1,3-dioxole.

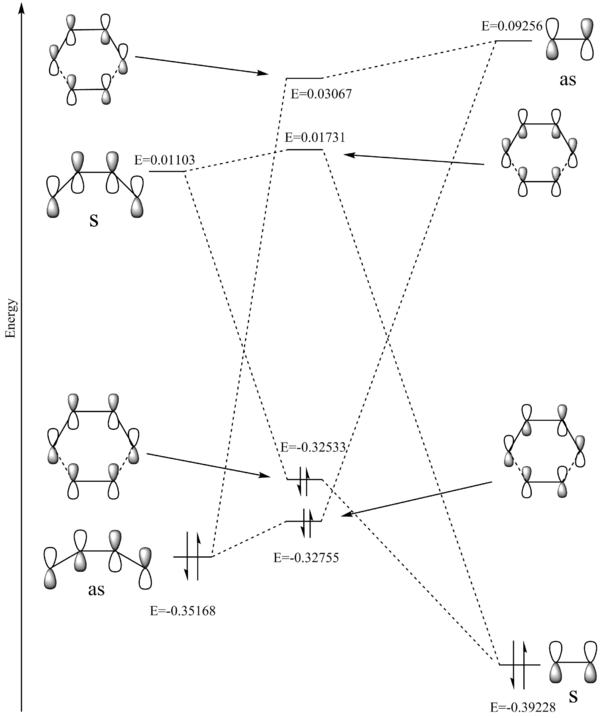
An MO diagram, shown in figure 11, was constructed after consideration of the reactant molecular orbitals which are displayed in figure 10.

Figure 10: Molecular orbitals of cyclohexadiene and 1,3-dioxole

Cyclohexadiene HOMO	Cyclohexadiene LUMO	1,3-Dioxole HOMO	1,3-Dioxole LUMO

As for the previous reaction, the new HOMOs and LUMOs are formed from the 1,3-dioxole HOMO and cyclohexadiene LUMO, as this pairing has the smaller energy difference (0.32545 au vs 0.3304). It is much more common in diels-alder reactions for the new HOMO and LUMO to be generated from the diene HOMO and dienophile LUMO. This is due to inverse electron demand. Usually the diene is electron rich, providing a high energy reactant HOMO, and dienophile electron poor, providing a low enrgy reactant LUMO. However in this situation, the dienophile is electron rich due to the adjacent oxygens, which donate electron density to the double bond. This raises the energy of its HOMO, decreasing the energy gap between it and the diene LUMO.

Nf710 (talk) 11:48, 9 February 2018 (UTC) This is the correct deduction, you could have shown this quantitively by doing a single point energy calc on the first point (reactants) of the irc.

Figure 11: Molecular orbital diagram for the endo and exo transition state.

(Fv611 (talk) I understand why you have shown the MO diagrams this way, and it is actually quite helpful in this case, but I have to advise against it as it is not chemically correct in this form (the number of FMOs and MOs do not match). However, you did well in considering both conformations.)

Comparison of the transition states show the endo HOMO has a slightly lower energy. This is because in the transition state the endo configuration has a much greater overlap between diene and dienophile, leading to stabilising interactions between the MO's. This is illustrated in figures 12 and 13. This becomes even more apparent when the secondary orbitals are considered, as seen in figure 14. There are large regions of overlap in the endo transition state in comparison to the exo.

Figure 12ː Endo transition state molecular orbitals

HOMO - 1	HOMO	LUMO	LUMO + 1

Figure 13ː Exdo transition state molecular orbitals

HOMO - 1	HOMO	LUMO	LUMO + 1

Figure 14ː Secondary orbital interactions

ENDO TS	EXO TS

Thermochemistry

Information about the kinetic and thermodynamic products of the reaction can be gained by examining the thermochemistry. Although the HOMO of the endo transition state is lower in energy it does not reveal which product is energetically more favourable. This was investigated by comparing product energies to the reactants. Further information about the reaction barrier was drawn by contrasting the transition state energies to the reactants also. These values are shown in table 1.

Table 1ː reaction barriers and energies for the reaction between cyclohexadiene and 1,3-dioxole

Stereoisomer	Reaction Barrier / kJ/mol	Reaction Energy / kJ/mol
endo	158.64	-66.09
exo	166.34	-62.61

The endo stereoisomer has both a lower reaction barrier and reaction energy. This means that not only is it formed more easily, but its product is also more stable. The lower reaction barrier is due to the previously discussed secondary orbital interactions. The fact it is a more stable product can be explained due to sterics. The oxygen-carbon-oxygen fragment in the exo product could be experiencing hindrance from the bridging carbons, which do not exist in the endo product as it is facing downwards.

Nf710 (talk) 11:51, 9 February 2018 (UTC) Your energies are correct(ish) and you have come to the correct conclusions. your jmols of the SSO are very nice. You couldhave added a diagram for the sterics.

Log Files

File:2HRC115 ENDOOFB3.LOG - endo product

File:6HRC115 EXOOFB3.LOG - exo product

Exercise 3ː Diels-Alder vs Cheletropic

Reactions

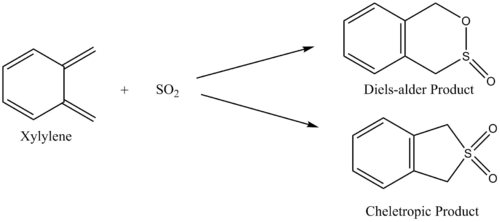
The reaction between sulfur dioxide and xylylene can either proceed as a hetero-diels-alder (producing either an endo or exo product) or as a cheletropic reaction, as demonstrated in figure 15.

Figure 15ː Scheme for the reaction between xylylene and sulfur dioxide.

The pathway of the transition states for each outcome is illustrated in figure 16.

Figure 16ː Transition state pathways for possible reaction outcomes

Endo	Exo	Cheletropic

Thermochemistry

An examination of thermochemistry provides information on the different energies, and therefore preferred products. This is shown in table 2 and figure 17. All enrgies are in kJ/mol.

Table 2ː Reaction Barriers and Energies

Product	Reaction Barrier / kJ/mol	Reaction Energy / kJ/mol
endo	82.76	-98.03
exo	86.75	-98.68
cheletropic	105.08	-154.99

Figure 17ː Comparison of rection barriers and energies

(Don't forget units! Tam10 (talk) 14:33, 4 February 2018 (UTC))

The endo product has the lowest reaction barrier, but is also the least stable product. The cheletropic reaction has the highest reaction barrier, but is the most stable product due to bond energies.

Table 3ː Bond strengths

Bond	Energy / kJ/mol
C-O	358
C-S	272
C=S	522

(Small typo in table Tam10 (talk) 14:33, 4 February 2018 (UTC))

Table 3 shows the bond strengths relevant to this reaction. In the diels-alder reactions, new C-O and C-S bonds are formed, and there is a loss of one S=O double bond. The cheletropic involves the formation of two new C-S bonds. Despite the C-O bonds being stronger than the C-S, the diels-alder product involves the loss of a very strong S=O double bond. This overrides the reaction energies, making the cheletropic product more stable. However, it has the highest reaction barrier as it has the most twisted and strained transition state, due to having a smaller ring size than the diels-alder.

Xylylene is a very unstable molecule. Looking at the IRC pathways, as soon as the sulfur dioxide approaches, but before it bonds, xylylene changes its bonding character to become aromatic, a much more stable structure.

Log Files

File:HRC115 SOBER1.LOG - exo transition state

File:HRC115 NSOFR.LOG - endo transition state

File:HRC115 CHXBER.LOG - cheletropic transition state

Conclusion

The transition states geometries that occur in reactions between butadiene and ethylene, cyclohexadiene and 1,3-dioxole, and xylylene and sulfur dioxide were succesfully found using Gaussview. Those reactions occuring in exercises 1 and 3 were optimised using the PM6 method, and those in exercise 2 were further optimised using the B3LYP method. In exercise 1, the differences in bond lengths throughout the reaction were examined, and when compared to typical carbon bond lengths, they tally with what we would expect. Inspection of molecular orbital energies in exercise 2 reveals that this reaction proceeds with inverse electron demand, and it is the HOMO of the dieneophile that contributes to the new HOMO in the product, rather than the HOMO of the diene. This is because 1,3-dioxole is electron rich (dieneophiles are usually electron poor), which raises its HOMO energy. Exercise 3 shows that despite the endo diels-alder product having the lowest reaction barrier, it is the least stable product. The cheletropic product, which has a high reaction barrier due to its strained transition state geometry, it the most stable as it retains both strong sulfur-oxygen double bonds.