Rep:Grt07:breakyourself3

The Cope Rearrangement

The Cope rearrangement of 1,5-hexadiene is to be investigated. The Cope Rearrangement involves a [3,3]-sigmatropic rearrangement of 1,5-dienes. The reaction takes place via a concerted pericyclic reaction involving either the chair or boat configuration transition state. The low energy minima and transition structures on the C6H10 potential energy surface are to be calculated and from this, the preferred reaction mechanism will be deduced.

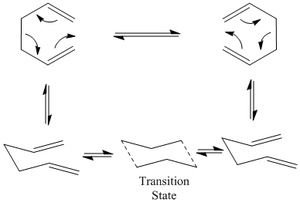
1,5-dienes can rotate freely around the three central C-C bonds and hence many different conformers can be formed.

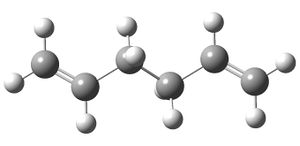a) A molecule of 1,5-hexadiene was built with an anti-periplanar relationship along the central C-C bonds, the structure cleaned and then optimised using the Hartree-Fock method with a 3-21G basis set (http://hdl.handle.net/10042/to-6146) the results are shown below:

Calculation Type FOPT
Calculation Method RHF
Basis Set 3-21G
Total Energy -231.692535 Hartrees
RMS Gradient Norm 0.00001891 Hartrees
Dipole Moment 0 Debye

The symmetry of the optimised molecule was Ci which labelled as anti2 in appendix 1.

b) Another molecule of 1,5-hexadiene was built, this time with a gauche relationship along the central C-C bond. This molecule was optimised in the same way with the following results (http://hdl.handle.net/10042/to-6343):

Total Energy -231.6915
RMS Gradient Norm 0.00001866
Dipole Moment 0.1281
Symmetry C2

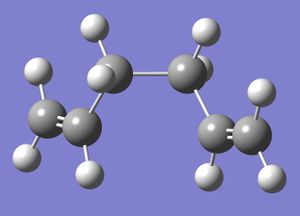The energy of the resulting conformation is marginally higher than that of the initial Ci conformer which is what would be expected as the hydrogens are in a gauche conformation along the 3 central C atoms and this usually results in a higher energy relative to an anti periplanar conformation due to the increased steric clashing.

c) Next, an attempt was made to creat the most stable conformation of the 1,5-hexadiene molecule. This was done by examining appendix 1 and manually altering a pre-optimised 1,5-hexadiene molecule in a similar way to the most stable gauche 3 molecule with C1 symmetry. This was then optimised using the Hartree Fock method with a 3-21G basis set (http://hdl.handle.net/10042/to-6322):

Calculation Type FOPT
Calculation Method RHF
Basis Set 3-21G
Total Energy -231.69266 Hartrees
RMS Gradient Norm 0.00000301 Hartrees
Dipole Moment 0.3405 Debye

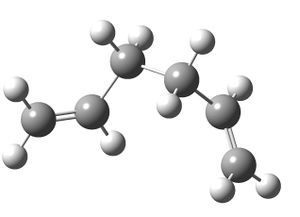This is indeed the lowest energy conformation I could make after a few attempts at manually arranging the atoms slightly differently before optimising the molecules in the same way (http://hdl.handle.net/10042/to-6329).

The fact that the lowest energy conformer (using the HF/3-21G method) is in a gauche arrangement is surprising as this usually leads to a higher energy molecule due to increased steric clashing between the hydrogens on the carbon atoms. This stability must be due to different interactions which have a greater stabilising effect on the total energy of the molecule than the destabilising effect of the steric clashing. This stabilising interaction is probably some sort of hyperconjugation effect from the C-H sigma orbitals into a different part of the MO structure.

This conformation was optimised again using a 6-31G basis set (http://hdl.handle.net/10042/to-6310):

Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 6-31G
Total Energy -234.5597 Hartrees
RMS Gradient Norm 0.00004135 Hartrees
Dipole Moment 0 Debye

The resulting structure was very similar to with the HF/3-21G method and still had Ci symmetry. However, the more accurate 6-31G basis set gave a much lower total energy.

A frequency calculation was then undertaken on this more accurately optimised conformer with the same level of theory (http://hdl.handle.net/10042/to-6309). The spectrum is shown along with the thermochemistry data:

Sum of electronic and zero-point energies= -234.416218
Sum of electronic and thermal energies= -234.408933
Sum of electronic and thermal enthalpies= -234.407988
Sum of electronic and thermal Free Energies= -234.447812

Optimizing the Chair TS Conformation

The transition state in the Cope rearrangement can adopt two conformations and, therefore, we will compare the two conformations and determine which transition state is the lowest in energy and hence which transition state the reaction goes by.

The transition states are essentially two allyl fragments of CH2-CH-CH2. The fragment was built using Gaussview and optimised using a Hartree Fock method with a 3-21G basis set (http://hdl.handle.net/10042/to-6342):

Calculation Type FOPT
Calculation Method UHF
Basis Set 3-21G
E(UHF) -115.823
RMS Gradient Norm 0.00005432
Dipole Moment 0.0291 Debye
Point Group C1

Two of these fragments were then used to predict the chair transition state of the Cope rearrangement by arranging them in a similar way to the predicted transition state. There was roughly a 2.2A gap between the terminal carbons. This structure was optimised using a Hartree Fock Method

An Opt+Freq calculation was then run through Gaussian (http://hdl.handle.net/10042/to-6341) with the options: optimize to a transition state (Berny); The force constants calculated once; and the keywords 'Opt=NoEigen' which stops the calculation crashing if more than one imaginary frequency is detected during the optimisation. The resulting output had the properties:

Calculation Type FREQ
Calculation Method RHF
Basis Set 3-21G
Total Energy -231.619
RMS Gradient Norm 0.00000941
Imaginary Freq 1 (-817.938cm-1)
Dipole Moment 0.0001 Debye

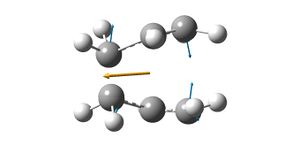
The transition structure estimate was then optimised in a different way. Both pairs of terminal carbons were given frozen coordinates and then the optimisation run again (http://hdl.handle.net/10042/to-6340).

Calculation Type FOPT
Calculation Method RHF
Basis Set 3-21G
Total Energy -231.615 Hartree
RMS Gradient Norm 0.00326 Hartree
Dipole Moment 0.0018

The transition state estimate was then optimised again in a different way. Both pairs of terminal carbons were given frozen coordinates of 2.2A, the optimisation set to a minimum and the force constants never calculated then the optimisation run again(http://hdl.handle.net/10042/to-6337).

Calculation Type FREQ
Calculation Method RHF
Basis Set 3-21G
Total Energy -231.619
RMS Gradient Norm 0.00005190
Imaginary Freq 1
Dipole Moment 0.0009

The resulting molecule had one imaginary frequency of -818.104 which corresponds to the vibrations of the terminal carbons relative to the terminal carbons opposite. This confirms that the molecule formed is the chair transition state for the Diels-Alder reaction.

Optimisation of the Boat Transition State

Two of the 1,5-hexadiene molecules with Ci symmetry created in the first part of the investigation were then placed in the same molecule group (one as the reactant, one as the product). The atoms of the product molecule were renumbered so that they correspond to the reactant molecule after the reaction.

A QST2 calculation, in which reactants and products are specified and Gaussian interpolates between them and finds the transition state, was configured with the molecules optimised to a transition state (Berny) (http://hdl.handle.net/10042/to-6339). The calculation failed as the configuration of the reactant molecule was not close enough to the actual transition state.

Failed QST2 Boat Transition State Calculation

The molecule from the original input file was then altered in an attempt to make the reactant and product molecules closer to the actual transition structure. The molecules' central C-C-C-C dihedral angles were altered to 0 degrees and the inside C-C-C bond angles were reduced to 100 degrees. The same QST2 job was run again (http://hdl.handle.net/10042/to-6338) and this time was successful in finding the transition structure:

Calculation Type FREQ
Calculation Method RHF
Basis Set 3-21G
Total Energy -231.603 Hartrees
RMS Gradient Norm 0.00000567
Imaginary Freq 1
Dipole Moment 0.1584 Debye
Symmetry C2v

As for the chair transition structure, the imaginary frequency corresponds to the vibrations of the bonds between the 2 pairs of terminal carbon atoms and had a value of -839.957. This confirms that the transition state structure for the Cope rearrangement was found.

The energy of the boat transition state is higher than that of the chair conformation due to the eclipsed conformation of the carbon atoms which increases steric clashing between them and the attached hydrogen atoms. This suggests that the reaction proceeds via the chair transition state.

Intrinsic Reaction Coordinates

It is hard to predict which molecule is being formed from looking at the transition state alone. However, an Intrinsic Reaction Coordinate calculation can be undertaken which shows the minimum energy pathway from the transition state to the local minimum of the potential energy surface

The optimised chair transition state structure was taken and an IRC calculation undertaken (https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/to-6306). The reaction coordinate is symmetrical for the forward and backward reactions so the reaction coordinate was only calculated for the forward direction. The force constants were calculated once and the number of points along the IRC calculated set to 50.

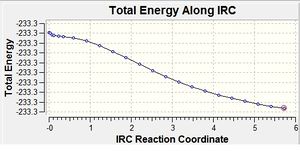
It was presumed that the minimum structure had not been found initially because the IRC graph had not reached a plateau after the 23 points and hence, in an attempt to find this desired minimum, the force constants were always calculated rather than once like in the initial IRC calculation (http://hdl.handle.net/10042/to-6322). This method was chosen because only 23 points were required for the initial IRC calculation so adding more points would be pointless. This method should give the most accurate result so it was chosen over the other suggested method of taking the structure from the initial IRC calculation and optimising that. As a precaution the number of points was set at 100.

The resulting output had the results:

Calculation Type FREQ
Calculation Method RB3LYP
Basis Set 3-12G
Total Energy -233.33524 Hartrees
RMS Gradient 0.00002156
Dipole Moment 0.3885 Debye

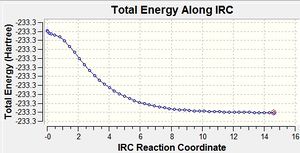
By looking at the 2nd IRC Graph we can see that the IRC calculation came to a plateau which suggests that a minimum was reached.

Looking at the final structure of the 2nd IRC calculation, it looks as though either the gauche2 or gauche4 conformations with C2 symmetry is being formed. The symmetrise function was undertaken on the final IRC structure and this also came back with the result that this structure had C2 symmetry although it would be hard to determine which gauche structure is being formed.

Activation Energies

The activation energies for the reaction will now be calculated using both the lowest energy chair transition state and the boat transition state.

Both the chair and boat transition structures were reoptimised using a higher level of theory. A B3LYP method with a 6-31G basis set was used (chair http://hdl.handle.net/10042/to-6308 and boat http://hdl.handle.net/10042/to-6307). The output file was taken and the following values used to find the activation energy.

Chair TS thermochemistry data:

Sum of electronic and zero-point Energies=           -234.362676
Sum of electronic and thermal Energies=              -234.356764
Sum of electronic and thermal Enthalpies=            -234.355819
Sum of electronic and thermal Free Energies=         -234.391604

Boat TS thermochemistry data:

Sum of electronic and zero-point Energies=           -234.351356
Sum of electronic and thermal Energies=              -234.345053
Sum of electronic and thermal Enthalpies=            -234.344109
Sum of electronic and thermal Free Energies=         -234.380121

1,5-Hexadiene thermochemistry data:

Sum of electronic and zero-point Energies=           -234.416218
Sum of electronic and thermal Energies=              -234.408933
Sum of electronic and thermal Enthalpies=            -234.407988
Sum of electronic and thermal Free Energies=         -234.447812

Using the difference between the Sum of electronic and thermal Free Energies for each TS and the anti2 1,5-Hexadiene reactant we get:

Chair Transition State Activation Energy = 0.056208 Hartrees = 35.27 kcal/mol at 0K
Boat Transition State Activation Energy = 0.067691 Hartrees = 42.48 kcal/mol at 0K

From the results it has been found that the activation energies for the Cope rearrangement are lower for the chair transition state pathway rather than the boat transition state. This fits in with the predictions made earlier that took into account the fact that there was more steric clashing associated with the boat transition state and hence it it higher in energy.

If we compare the values found to the experimaental values of 33.5 ± 0.5 kcal/mol via the chair transition structure and 44.7 ± 2.0 kcal/mol via the boat transition structure at 0 K it can be said that the modelled values are reasonably close to the experimental values using the B3LYP/6-31G level of theory. The computed values probably wouldn't be as close to the experimental data if a lower level of theory such as the 3-21G basis set was used to calculate the activation energies.

Diels Alder Investigations

The Diels Alder reaction is a cycloaddition reaction between a conjugated diene and a dienophile. It is a pericyclic reaction which proceeds via the transition state and this is to be investigated.

The first reaction to be investigated is that of cis-butadiene with ethylene. Gaussview was used to construct a cis-butadiene molecule and optimised using the AM1 semi-empirical MO method (http://hdl.handle.net/10042/to-6333):

Calculation Type FOPT
Calculation Method RAM1
Basis Set ZDO
Total Energy 0.0488 Hartrees
RMS Gradient Norm 0.00001745
Dipole Moment 0.0414 Debye
Symmetry C2v

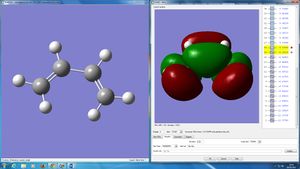
The HOMO and LUMO were plotted and the symmetries determined with respect to the sigma-v plane:

Butadiene HOMO - Antisymmetric
Butadiene LUMO - Symmetric
Ethylene HOMO - Symmetric
Ethylene LUMO - Antisymmetric

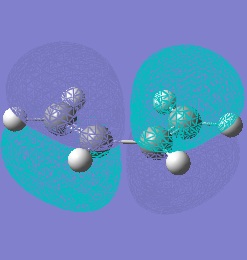
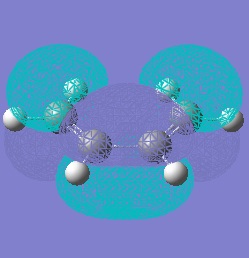
Molecular orbitals only interact if they have symmetries which complement each other. If we look at the HOMOs and LUMOs of both reactant molecules we can see that the HOMO of cis-butadiene can interact with the LUMO of ethylene and vice versa.

The transition state for the Diels-Alder reaction was then computed using the optimised butadiene molecule and an optimised (http://hdl.handle.net/10042/to-6331) ethylene molecule arranged in a similar way to the predicted transition state. The method used was Hartree Fock with a 3-21G basis set and the TS(berny) job type used (http://hdl.handle.net/10042/to-6321):

Calculation Type FREQ
Calculation Method RHF
Basis Set 3-21G
Total Energy -231.603 Hartrees
RMS Gradient Norm 0.00001954
Imaginary Freq 1
Dipole Moment 0.5756 Debye

The transition structure had one imaginary frequency of -818.48 which corresponds to the movement of the ethylene carbons towards the terminal butadiene carbons with the hydrogens bonded to these carbons moving away from where the new C-C bonds will form. This confirms that the structure found is the transition state.

The HOMO and LUMO of the transition states were computed:

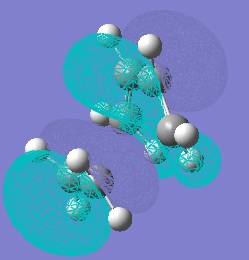
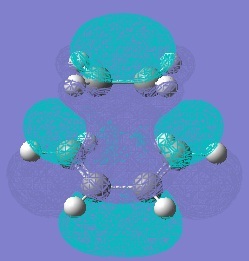
The HOMO of the transition state is antisymmetric and hence it must have been formed from the HOMO of cis-butadiene and the LUMO of ethylene. However, the LUMO of the transition state is symmetric so must have been formed from the LUMO of butadiene and HOMO of ethylene.

The bond lengths and angles of the starting materials used; the transition state; and the literature values were then compared (brackets signify literature values):

Newly formed C-C sigma bond

Butadiene 2.2
Ethylene 2.2
Transition State Butadiene 2.20987
Transition State Ethylene 2.20987
The bond lengths are very similar for the transition state and starting materials. If we compare the TS C-C bond lengths for butadiene with the newly forming C-C bond it is clear that the newly forming bond length is much longer. This is because the bond has not fully formed yet and therefore the bond is not as strong, and hence longer, as it will be when the reaction has taken place.

C=C pi bonds

Butadiene 1.33507 (1.349)
Ethylene 1.326 (1.329)
Transition State Butadiene 1.36999
Transition State Ethylene 1.37589
Both C=C bond lengths are longer in the TS than in the starting materials. This is because the C=C bonds become C-C sigma bonds in the product which are longer than the pi-bonds. The transition state C=C bonds are in the process of becoming C-C sigma bonds so are longer than the starting materials but are not yet as long as the final sigma C-C bonds will be. The literature values are close to the calculated bonds of the starting materials but will of course be different to the final product.

Initial C-C sigma bond

Butadiene 1.44946 (1.467)
Ethylene -
Transition State Butadiene 1.39443
Transition State Ethylene -
The butadiene single C-C bond is longer in the starting product than in the TS because the bond is in the process of becoming a pi C=C bond in the product and C=C bonds are shorter than C-C bonds. The calculated C-C bond in butadiene is reasonably close to the literature value but if a higher level of theory the calculated bond would probably be closer to this literature value.

C=C-C angle

Butadiene 125.665 (124.4)
Ethylene -
Transition State Butadiene 121.472
Transition State Ethylene -
This angles decreases from the starting butadiene molecule to the TS because the product molecule is a 6 membered ring structure which in general have smaller bond angles than non-ring structures. Again, the computed value is reasonably close to the literature value but would probably be improved if a higher level of theory was used.

C=C-H angle

Butadiene 121.909 (120.9)
Ethylene 122.725 (120.9)
Transition State Butadiene 119.958
Transition State Ethylene 119.760
In a similar fashion to the C=C-C bond angle, the bond angle decreases in the TS relative to the starting material and this again is due to the forming ring structure from the TS.

The Diels Alder reaction of cyclohexa-1,3-diene reaction with maleic anhydride

The reaction of cyclohexa-1,3-diene with maleic anhydride is a stereoselective Diels Alder reaction where the endo product is the mojar product. Because the reaction is kinetically controlled, the energies of the exo and endo transition states are to be investigated. As the endo product is the major product then the transition state involved must be lower in energy than that of the exo conformation i.e. the reaction has a lower activation energy.

Molecules of cyclohexa-1,3-diene and maleic anhydride were created in gaussview and optimised using the Hartree Fock method and a 3-21G basis set (http://hdl.handle.net/10042/to-6318 and http://hdl.handle.net/10042/to-6332). These optimised molecules were then arranged next to each other in an attempt to estimate the structure of the endo transition state in the Diels-Alder reaction. An opt+freq calculation (http://hdl.handle.net/10042/to-6320) was then run with a view to finding the optimised transition state using the Hartree Fock method and 3-21G basis set and optimising to a transition state (Berny). The results are shown below:

Calculation Type FREQ
Calculation Method RHF
Basis Set 3-21G
Total Energy -605.610 Hartrees
RMS Gradient Norm 0.00002292
Imaginary Freq 1
Dipole Moment 6.7145

There was one imaginary frequency at -643.58cm-1 which corresponds to the stretching of the newly forming bonds between the expected carbons.

The optimisations of the transition state were then run again with different methods: semi imperial with a ZDO basis set (http://hdl.handle.net/10042/to-6316) and B3LYP with a 6-31G basis set (http://hdl.handle.net/10042/to-6315):

semi imperial with a ZDO basis set:

Calculation Type FREQ
Calculation Method RAM1
Basis Set ZDO
Total Energy -0.05150 Hartrees
RMS Gradient Norm 0.00000769
Imaginary Freq 1 (-806.393)
Dipole Moment 6.1664 Debye

B3LYP with a 6-31G basis set:

Calculation Type FREQ
Calculation Method RB3LYP
Basis Set 6-31G
Total Energy -612.495 Hartrees
RMS Gradient Norm 0.00000691
Imaginary Freq 1 (-446.825)
Dipole Moment 7.0090 Debye

The process was repeated to find the exo adduct ():

Calculation Type FREQ
Calculation Method RHF
Basis Set 3-21G
Total Energy -605.6036 Hartrees
RMS Gradient Norm 0.00004883
Imaginary Freq 1
Dipole Moment 5.9379

Again there was one imaginary frequency, this time at -647.211cm-1, which corresponds to the stretching of the newly forming bonds between the expected carbons.

The optimisations of the transition state were then run again with different methods: semi imperial with a ZDO basis set (https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/to-6313) and B3LYP with a 6-31G basis set (http://hdl.handle.net/10042/to-6314):

Semi imperial with a ZDO basis set:

Calculation Type FREQ
Calculation Method RAM1
Basis Set ZDO
Total Energy -0.05042 Hartrees
RMS Gradient Norm 0.00001456
Imaginary Freq 1 (-812.311)
Dipole Moment 5.5642 Debye

B3LYP with a 6-31G basis set:

Calculation Type FREQ
Calculation Method RB3LYP
Basis Set 6-31G
Total Energy -612.491 Hartrees
RMS Gradient Norm 0.00000596
Imaginary Freq 1 (-448.357)
Dipole Moment 6.3940 Debye

Comparing the total energies of the transition states gives the expected result of the endo transition state being lower in energy using all 3 different methods of calculation. The exo transition state structure being higher in energy results from the bridgehead of the cyclohexadiene ring being on the same face as the 3 oxygen atoms on the maleic anhydride fragment which increases streric clashing in the total structure and hence increases the energy.

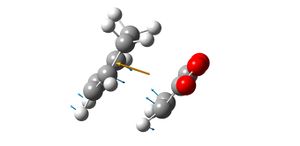
Molecular Orbitals of Maleic Anhydride, Cyclohexa-1,3-diene and the Exo and Endo Transition Structures

A study of the molecular orbitals of the reactants and transition states of the reaction helps to understand how the product is formed. The HOMOs and LUMOs of the reactant molecules and the transition states were computed and their symmetries determined (symmetries indicated on thumbnail titles).

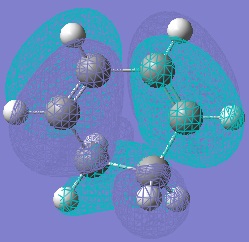
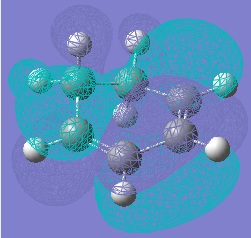
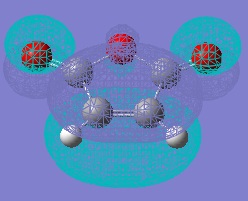
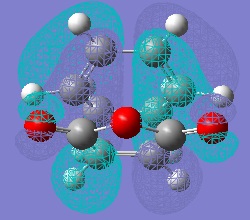
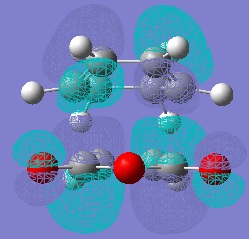
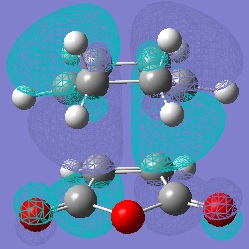
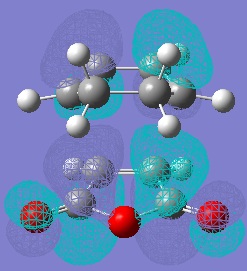
By studying the molecular orbitals it can be understood that it is the HOMO of the cyclohexa-1,3-diene and the LUMO of the maleic anhydride that combine to form the transition states as they have the same symmetry. By studying the MOs we can also see another erason why the endo transition state is more stable. Aside from the primary orbital overlap which creates the new bonds, there is also secondary orbital overlap between the pi orbital of the C=O groups in the endo transition state with the pi orbitals on the cyclohexa-1,3-diene which creates additional stabilisation of the endo transition state. These stabilising interactions are not present in the exo-transition state due to the C=O groups on the maleic anhydride fragment located away from the diene. The partially formed C-C Bond Lengths were calculated to be 2.16243 Angstroms for the endo TS and 2.17030 Angstroms for the exo TS.