Rep:Ggr07Module3:version1
Module 3 (Physical)
The Cope Rearrangement
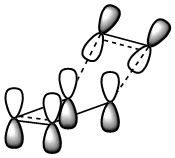
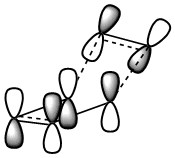
Gauche and Antiperiplanar conformations of 1,5-Hexadiene
| Anti periplanar | |
| Energy (a.u.) | -231.69254 |
| Point Group | Ci |
| Gauche | |
| Energy (a.u.) | -231.68772 |
| Point Group | C2 |
A conformation in which all the four back carbons (i.e. the non-terminal carbonds) are bonded in an antiperiplanar conformation was optimised with HF (Hartree-Fock) with a basis set of 3-21G and found to have symmetry of the point group Ci which is a very low symmetry having it's identity and a center of inversion only.
This conformation can be compared with other isomers. Of all the potential rotamers an antiperiplanar arrangment is expected to be the most stable due to minimisation of steric clash.
The same method was followed by positioning all the four back carbons gauche to each other. The structure was optimised as in the previous case to obtain a conformation with increased symmetry of C2. Due to the two products being isomers of each other the energies can be directly compared and have a difference in value of 12.65491kJ/mol. As predicted the antiperiplanar structure is most stable.
Counterintuitively there is however a gauche structure which is the most stable of all confomers this is due to the specific confomers ability to tautomerise via a cope rearrangment.
Further Optimisation of the Anti2
| 2nd opt | Antiperiplanar |
| Energy (a.u.) | -234.61171 |
| Point Group | Ci |
| 298.15K | 0K | |
| E0K | -234.469 | not available |
| E298.15K | -234.462 | not available |
| H | -234.461 | not available |
| G | -234.501 | not available |
The previous anti product was further optimised by increasing the basis set for a better desription of the Molecular Density. The calculations were made with a different method of DFT instead of HF with a higher basis set of 6-31G. The geometry is very similar and therefore there is only minor refinement to the geometry. The energy is reduced due to a lower potential minima found with higher accuracy calculations. Thermochemical data can be obtained from the resulting optimised date. The values are defined as; E0K is the sum of electronic and zero-point energies, E298.15K is the sum of electronic and thermal energies, H is the sum of electronic and thermal enthalpies and finaly G is the sum of electronic and thermal free energies. These energies can be compared with other isomers if the same basis set and method of calculation is used.
Several attempts[1][2][3][4][5] were made to compute the Thermochemical properties at 0K but unsuccesful (even just altering the temperature[6]). Therefore it can only be estimated that at 0K the 0.007K increase in (negativity) potential energy will be due to the reduction in the number of accesible vibrations. It is estimated that at 0K that there would be a single residual vibration of the molecule which has to exist if the molecule exists.
Chair and Boat Transition States
So far only the product (isomers) of rearrangement has been studied. However the transition state of these reactions can be analysed theoreticaly as well as the product. There is more than one possible reaction path way for this cope rearrangement i.e. two transition states and the activation energies and enthalpies of these transition states can be followed.

The two transitions states are either a chair conformation or a boat conformation. In this section different methods will be utilized and compared for computing the properties of these transition states.
Optimising the 1,5-hexadiene chair transition state
An allyl fragment of (CH2CHCH2) was optimised using Hartree-Fock method and a low level 3-21G basis set[7]. The optimised fragment was then copied and two were amalgamated to form an approximate transition state for the chair structure with an aproximate distance of 2.2Angstrom between terminal carbons of both allyl fragments.
Two optimisation methods will now be utilised (and subsiquently compared) for the optimisation of this transition state (using the same basis set of 3-21G).
Hessian Method
The first is the optimisation of the chair transition state by computing the force constant matrix (Hessian) which is re-calculated as the conformation is altered in every step. It is important that the guess structure is fairly accurate/correct because a false minimum can be obtained easily by virtue of this method.
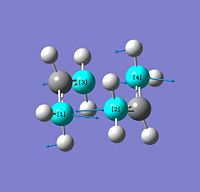
The guess structure was optimisied using TS (Berny) and frequency analysis was made on the optimised structure. The resulting six low frequencies were checked and 5 were all below the modulus of 10KJ/mol confirming that an optimised minima had been reached.
A single imaginary frequnecy (>10kJ/mol) of -818cm-1 was obtained from the frequency calculation. This vibration represents the bond breaking/forming which happens during the reaction. Vibrations in molecules have downaward slopes explaining their energy minimum however this single negative/imaginary stretch is due to the force constant being negative therefore the lowest energy is not at the equilbrium of the stretch (i.e. the transition state) but at extremes which is the product or starting conformation.
As seen in the image during the inital "contraction" the 1 and 2 carbon atoms are forming a σ bond while the 3 and 4 are breaking and vice versa on the "expansion".
Frozen Coordinate Method
The guess structure of the chair TS will now be optimised using a different method. During the [3,3] Sigmatropic rearrangement the σ bond forming and breaking's distances can be frozen and the rest of the transition states geometry can be optimised. By implementing this method a poorer guess as to the geometry can originaly be suggested.
Both of these σ bonds were frozen to 2.2Angstrom and then optimised using the energy minimum optimisation (HF and same basis set).[8] Giving the resulting optimised geometry which was very similar to the transitions state calculated earlier.

The bonds were then defrosted (haha) and left free to be optimised via derivative (normal guess Hessian) without calculating the force constant which would alter the rest of the pre-optimised structure. The resulting bonds were optimised[9].
| Freeze Coordinate Method | TS (Berny) Directly | Difference | Units | |
| C-C Bond Length (Angstrom) | 2.02 | 2.02 | 0 | Angstrom |
| Energy at 0K (hartree) | -231.619322 | -231.619322 | 0 | Kcal/mol |
The carbon bonds formed and broken during the reaction are the refernced ones in the table above. As it can be observed both methods have been able to derive the same minimum and give the same values for the transition state. Therefore if the guess structure is accurate enough either method is equaly as good however the direct TS (Berny) method gives greater scope for a false minimum.
Optimising the 1,5-hexadiene boat transition state
Another transition state optimisation method will be used for calculating the boat transition state. A Synchronous Transit-Guided Quasi-Newton (STQN) Method is to be implemented and specificaly QST2 is the method to be used. The advantages of the chosen method is that the transition state does not have to be guessed only the reactant and products. The atoms need to be labeled in order to be tracked during the reaction and are done so for the antiperiplanar conformation obtained in the first section of the optimisation of 1,5-Hexadiene.


Interestingly the job fails to obtain the correct transition state structure shown below. This is due to the incorrected assumption during optimisation to translate one allyl fragment instead of rotation around the central bonds. Therefore this rotation must be implemented in to the conformation of the starting conformation and product in order to obtain the required transition state.
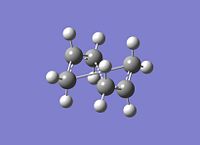
The central four carbons dihedral angles were rotated to 0 degrees and the two internal angles of these four carbons changed to 100 degrees. From this suggested geometry the QST2 optimisation was calculated. [10]

Intrinisic Reaction Coordinate of the transition state of the boat and chair
It is not possible to predict the conformation of product and reactant by analysing the boat and chair conformations. However there is a method of deriving the conformations by making small geometry optimisations to the Transition State and for each step looking for the steepest gradient of change in energy once found iterated again until a energy minimum is found which is the predicted product.
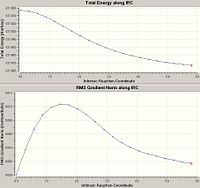
The resulting IRC is found to have not reached a minimum in energy (it only reached 21 points before concluding that it had converged even though 50 points were set) and therefore alterations to the IRC calculation initialy made is required.
There are multiple options for how the geometry can be further optimised.
- The final lowest energy geometry can be further optimised using normal optimisation
- The number of IRC points can be increased with the hope a minimum is found within the specified points.
- Finaly the force constant can be calculated each time to find a maximum gradient in fewer points.
The options are modeled on the boat conformation and then the best choice chosen for the chair. Attempts have been made at all three methods in order to discuss.
1. The final geometry in the IRC was then optimised using HF-3-21g TS (Berny) to give the resulting structure.
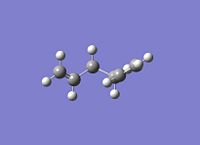
This is the tautimer of the gauche3 referenced in the appendix here[11] which has been correctly found. This option has been able to find the correct low energy optimisation but this is likely only because the last geometry is far across the IRC.
2.An attempt was made at increasing the number of points along the IRC to 75[12] however it is recognised that the IRC stopped after 21 and therefore would not expect increasing the points from 50 to 75 to make a difference. Therefore an attempt was made with a tighter convergence limit using "int=ultrafine scf=conver=9". But returned the same 21 IRC points as found originaly in the calculation[13].
3.The IRC was recalculated from the boat TS but this time with the force constant calculated after every point[14]. Interestingly zero derivative was not reached for the boat conformation even though the force constant was calculated infact after 42/43 the gradient increases.

Even though the IRC of bullet point 3 didn't reach the optimised geometry it is believed to give the most reliable answer for the geometry of the product and therefore is used for the chair conformation.
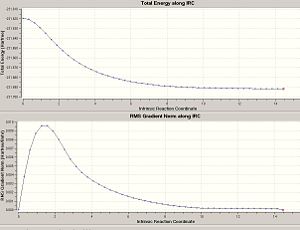
The chairs IRC was calculated[15] using point 3. Interestingly with the chair conformation the energy minimum was reached giving the resulting conformation after 47 IRC points.
Higher Basis Set optimisation
The activation energy of these optimised structures can be obtained from the predicted transition structures. In order to have good estimates of the activation energy these optimised structures need to be further optimised with a larger basis set. Density Functional Theory is applied with the B3LYP method and a larger basis set of 6-31G(d) is used. The optimisiation was done for the chair[16] and boat[17] conformations.
| Boat TS (HF 3-21G) | Chair TS (HF 3-21G) | Boat TS (DFT 6-31G)[1] | Chair TS (DFT 6-31G)[2] | |||||
| E0K | -231.45092 | -231.466701 | 9.90272 | kcal/mol | -234.40234 | -234.414919 | 7.893435711 | kcal/mol |
| E298.0K | -231.4453 | -231.461341 | 10.06587 | kcal/mol | -234.396006 | -234.408998 | 8.152596928 | kcal/mol |
The chair conformation is observed to be significantly lower in energy ~10kcal/mol. And the increased basis set gives lower energy conformations as the minimum well is found more accurately. Due to unsuccesful attempts previously at calculating the thermochemichal properties at different temperatures this was not done.
The Diels Alder Cycloaddition
In this section Diels Alder cycloaddition reactivity will be studied via computational methods. They will be studied by modeling and analysing the transition states' structures of different dienes and dieneophiles.
During the discussion of this reactivity only elements up to Oxygen are expected to be considered. Based on this conclusion it was decided to do all final structure optimisations with Density Functional Theory with B3LYP method of calculation and a large basis set of 6-31g(d). This level of optimisation should yield high accuracy and if there were a need to expand the calculations to higher row elements the inclusion of the (d) in the basis set would accomodate for them.
For convenience all calculations for the Diels Alder are referenced at the end of the discussion.
The analysis of Cis Butadiene
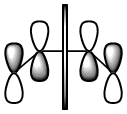
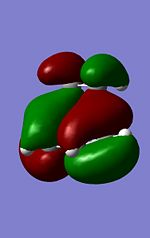
Cis butadiene is an example of a diene which is of correct geometry for the diels alder reaction (which more specificaly has the correct orbital alignment for a dieneophile to interact. The geometry was initialy optimised with AM1 semi-empirical checked to see if the energy had converged and then the final optimisation was run. The MO's of the HOMO and the LUMO are depicted below.
The LCAO's resemble the calculated MO's very well and it is observed that the HOMO is completely anti-symmetric with respect to the plane while the LUMO is completely symmetric with respect to the plane.

Diels Alder Transition State of Cisbutadiene and Ethene
The transition state of this particular Diels Alder reaction was derived by using the freeze coordinate method. An intuative guess as to the site of attack was made and the two sigma bonds formed during the reactions bond length frozen to 2.2Angstrom. The rest of the transition state was modified with B3LYP 3-21g basis set as rough estimate then further optimised to 6-31g(d) before using a guess Hessian to find the bond length of the previously frozen sigma bonds at the higher level basis set.
The advantages of this method is that with a slight intuative guess of the initial geometry the true energy minimum is found with greater certanty than TS(Berny) alone. QST2 is not chosen because an intuitive guess of the TS is possible and comparatively it is more likely to cause errors due to incorrect assignment of atoms or other inconsistencies between reagents and product.
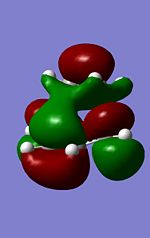
The MO's
It is worth noting that the local symmetry of the ethene and the cisbutadiene resemble the overall symmetry. Therefore analysing the frontier HOMO the symmetrical MO of cisbutadiene is therefore its LUMO and the corresponding frontier MO of Ethene is it's symmetrical HOMO. As both are symmetrical a concerted reaction is allowed. It can therefore be deduced that this reaction proceeds via a Ethene-Cisbutadiene HOMO-LUMO concerted reaction respectively.
Interestingly the HOMO MO has the majority of electron density at the forming alkene bond of the cis-butadiene and breaking alkene bond of the ethene (in the forward reaction) and therefore represents the transition between the two.
The Geometry
| Above | Side | Angle |
|---|---|---|
 |
 |
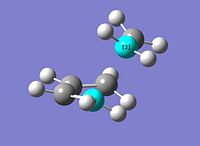 |
The predicted transition state very much resembels the starting reagents as opposed to being close to a planar six memebered ring of the product, it can be predicted from the previous statement that the reaction is expected to be exothermic. Both the bond lengths of TS forming carbon bonds are accurately estimated to be 2.27Angstrom. The bond lengths found experimentaly are sp3 being 1.526Angstrom[3] and sp2 1.47Angstrom[3] and Van der Waals radius of 1.75Angstroms[4] which would be 3.5Angstroms for both carbons. The value is observed inbetween this which would suggest that there is a shift in electron density (in the forward reaction sense) from the ethene to the cisbutadiene in one bond and vice-versa in the second explaining the transition states bond length while the covalent bond is formed (as the carbons change from being sp2 hybridised to sp3.).
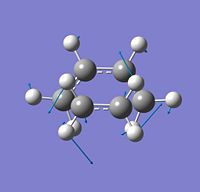
The Coordinate Path Vibrational Representation

Displayed is the imaginary frequency of the reaction coordinate vibration. As described earlier it is the only negative frequency calculated and signifies an energy maxima. The carbons of both species approach each other while the protons are pulled away when the stretch contracts forming sp3 hybridised orbitals. The frequency of the vibration is -525cm-1 which has a modulus which is larger than the first six positive vibrations.
It is observed from the imaginary frequency that both bonds have equal scalar with respect to their vectors therefore showing that the bonds are formed in a synchronus maner confirming that the reaction is concerted.
The lowest energy real vibration shows the displacement of the transition state which shows the rotation of the two reagents this would cause the reaction to occur via one carbon center first and wouldn't be a cyclic mechanism. The hypothetical reaction is drawn below. This is highly unlikely to occur as the orbital overlap of the transition state would be significantly reduced in the HOMO and the dipolar intermediate would be highly unstable.
The Regioselectivity of the Diels Alder Reaction
Cyclohexa-1,3-diene undergoes a diels alder raction with with dieneophile maleic anhydride and it's reactivity can also be studied. There are two possible regioisomers for the product depending on whether the maleic anhydride carbonyls are facing towards the forming alkene (endo) or away from the forming alkene (exo).
The structures below were used based on site of attack for the frozen coordinate method with the inital guess of 2.2Angstrom for the freezed bond length.
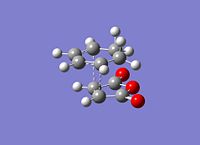
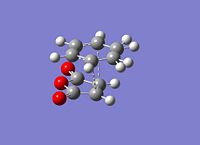
The exo had to be modified as the guess structure was not accurate enough guess as the CH2 can be seen to be much more sp3 hybridised than the guess of the endo structure. The important c-c bond lengths have been depicted for the exo(left) and endo(right). All bond lengths are in Angstrom and opposite sides are of the same value bond length due to the symmetry. It is observed that in both cases bonds involved in the cyclic reaction are all ~1.40Angstrom showing that the electron density is evenly distributed in the transition state. The two forming sigma bonds are however of different value the bonds are smaller. This would suggest a transition state closer to the product and that the two parts are drawn together closer at the transition state.
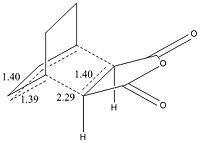
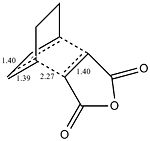

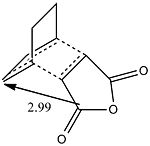
| EXO | ENDO | Difference | ||
| E0K | -612.498013 | -612.50214 | 2.589729643 | kcal/mol |
| E298K | -612.487662 | -612.491786 | 2.587847116 | kcal/mol |
| H | -612.486718 | -612.490842 | 2.587847116 | kcal/mol |
| S | -612.534266 | -612.538328 | 2.548941558 | kcal/mol |
It is known and has been calculated above that the Endo product is the kinetic product i.e. lower energy transition state. By analysing the strain from across this is contradictory as there seems to be more steric clash in the endo case rather than the exo as the carbonyls are closer to the nearest bridge. Therefore there is a need to look elsewhere as to the reasoning of the lower energy of the Endo product. It can be observed that the majority of energy difference is due to electronic contribution and therefore the MO's of these orbitals should be analysed.
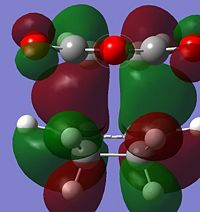
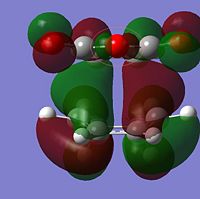
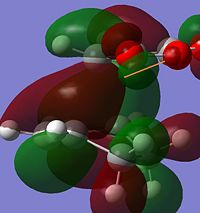
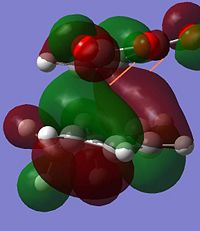
From observing the HOMO in both cases there is an interesting observation. The reason for the energy difference can be observed in the HOMO contributions to the HOMO's. It is due to the alignment of the oxygen group which can be observed when viewed down the nodal plane. In the ENDO case the oxygen clearly has delocalising effects towards the forming sigma bonds while there is little in the EXO case of this "secondary orbital overlap" as discussed in literature[5].
Table of Calculations
| 2nd Optimisation | Freeze (3-21G) | Freeze (6-31G) | Deriv (6-31G) | |
| Cisbutadiene | http://hdl.handle.net/10042/to-3591 | |||
| (Cis+Ethene) | http://hdl.handle.net/10042/to-3592 | http://hdl.handle.net/10042/to-3593 | http://hdl.handle.net/10042/to-3594 | |
| ENDO | http://hdl.handle.net/10042/to-3595 | http://hdl.handle.net/10042/to-3599 | http://hdl.handle.net/10042/to-3600 | |
| EXO | http://hdl.handle.net/10042/to-3598 | http://hdl.handle.net/10042/to-3596 | http://hdl.handle.net/10042/to-3597 |
References
- ↑ Values where not obtained and therefore taken from http://www.ch.ic.ac.uk/wiki/index.php/Mod:phys3
- ↑ Values where not obtained and therefore taken from http://www.ch.ic.ac.uk/wiki/index.php/Mod:phys3
- ↑ 3.0 3.1 A survey of carbon-carbon bond lengths, David RL Jr, Tetrahedron, Volume 17, Issues 3-4, 1962, Pages 125-134
- ↑ V.Yu. Zefirov, P.M. Zorkii. Russ. Chem. Rev. 58 (1989) 421–440.
- ↑ Steric Effects vs. Secondary Orbital Overlap in Diels-Alder Reactions, Marye Anne Fox,* Raul Cardona, and N. J. Kiwiet, J. Org. Chem, 1987,52, 1469-1474