Rep:Fizzychem
Module 3: The Transition State
The Cope Rearrangement
Anti- 1,5,-hexadiene was modelled and optimized using the HF method and 3-21G basis set. Its point group was assigned as C1 and its energy was -231.68907 hartree. This probably corresponds to anti 3 (shown in appendix 1), as it has the same energy. The point group is not the same, but since Gaussian is very fussy about point groups and will only assign a point group if the symmetry is perfect it is not that important.
Gauche 1,5-hexadiene was also modelled and optimized in the same way as the anti isomer. It was expected that this isomer would have a higher energy than the anti isomer, as there are more steric clashes between hydrogens. Its point group was assigned as C2 and its energy was -231.69166694 hartree. This corresponds most closely to the gauche 2 isomer (shown in appendix 1), as it has the same energy and point group.
Using the calculations above, the lowest energy conformation of 1,5-hexadiene should be anti. The lowest energy isomer that I could make had an energy of -231.69253524 hartree. This corresponded to anti 1, (had the correct energy), but the point group was not Ci. The molecule was then re-made and re-optimized. This time the correct symmetry was returned (the new energy of the molecule was -231.69253511 hartree, the same as reported in appendix 1 of the lab instructions).
This isomer having been found, it was optimized again using the 6-31G(d) basis set. The overall geometry of the molecule had changed very little, but the energy had changed quite substantially from that reported above to -234.61171551 hartree.
A frequency analysis was then done; this showed no imagninary frequencies. The energy of the molecule was also investigated using different corrections, these are shown below (copied from the log file).
Sum of electronic and zero-point Energies= -234.469176 Sum of electronic and thermal Energies= -234.461834 Sum of electronic and thermal Enthalpies= -234.460890 Sum of electronic and thermal Free Energies= -234.500744
Optimising the chair and boat transition states
The chair and boat transitions states were then modelled using different methods. These are disscussed below.
The chair transition state was modelled using two allyl fragments and placing them above one another as shown below.
The bond distance between the terminal carbons (that form bonds in the rearrangement) were set to 2.2 angstoms. This transition state was then optimized (to a Berny transition state) using the HF/3-21G basis set. This gave the transition state shown below. The vibrations were then checked to see if the appropriate transition state had been found. One negative vibration was found; this was at -817.884 cm-1 and corresponded to the forming and breaking of the bonds during the concerted rearrangement. This can be used to confirm that the structure found does correspond to the correct transition state.
A new transition state "guess" molecule copied from the orignial model that was used in the previous section. This was optimized using a frozen coordinate method; the "bonds" between the carbons that form/break new bonds were set to 2.2 angstroms long and frozen using the redundant coordinate editor. The rest of the structure was then optimized using the HF/3-21G method and basis set. Once this had optimized the frozen bonds were un-frozen and set to derivative instead. This time the transition state optimization was run using a guess Hessian at the important bonds. The force consants were therefore not computed at all. Once this optimization had completed it was possible to compare the two methods.
The boat transition state was optimized using the QST2 method, starting from the product and the reactant. At first the input used the optimized 1,5-hexadiene molecule with Ci symmetry as the reactant and the product (but re-labelled so that the carbons are correctly labelled in both). This did not work, however, as the Ci molecule does not have a close enough symmetry to the boat transition state. Instead, the Ci molecule had to be modified to be more like the transition state (the central dihedral angle was changed to 0 degrees and the inside C-C-C angles to 100 degrees.
This optimization completed showing a negative vibration at -1117.55 cm-1. It looked like it corresponded to the motion expected during the transition state, but the displacement vectors show that the vibration is not a pure stretch (there is a slight displacement of the other groups so the vibration is more of a bend). This doesn't seem to be as good a method of optimizing the transition state, as the input has to be fairly close to the actual structure of the transition state; if this is not known then it would be difficult to guess. Also, the negative vibration is not as pure a C-C stretch as was produced in the frozen bond method. It seems that the frozen bond method is easier to achieve the correct structure without knowing it to begin with. If the structure of the transition state were already mostly known then it may be quicker to use the QST2 optimization.
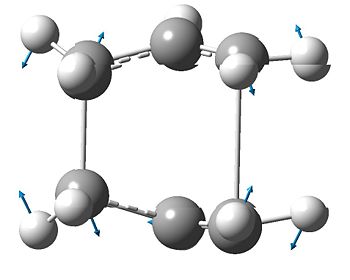
Comparing the two transition states and the mthods used to reach them, it is very difficult to deduce which conformer the transition state is formed from; this is especially evident when optimizing the structure using the QST2 method. In order to follow the geometry of the reactant as the reaction proceeds it is necessary to use the intrinsic reaction coordinate function in Gaussian. This shows the small steps along down the steepest slope of the potential energy surface that Gaussian has taken in order to minimise the geometry. The structure that has been taken to show the IRC is the chair transition state that was optimized using the frozen coordinate method. In this case the IRC was only calculated in one direction as it is symmetrical and the number of points along the IRC was changed from the default setting of 6 to 50. The resulting IRC is shown below.
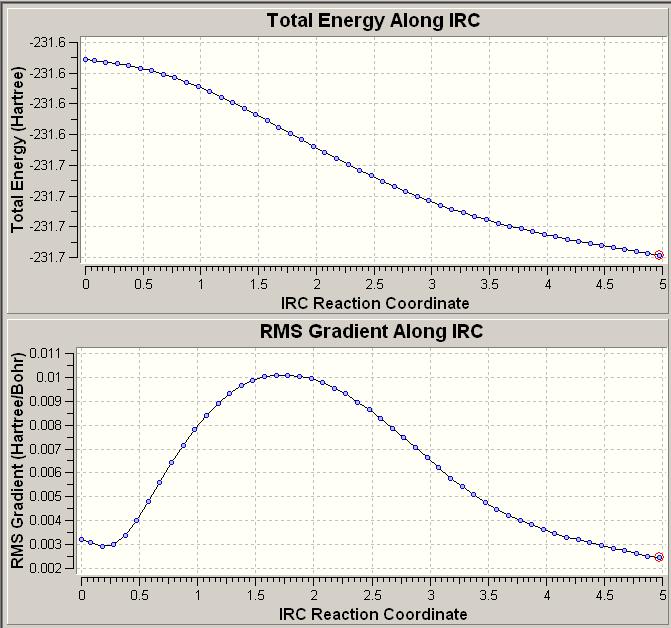
It can be seen from this that the IRC had not yet reached a minimum geometry. This is because the number of points chosen to be calculated was not enough. From this point there are a few options: to run a normal minimization from the final geometry, to run a second IRC this time chosing to calculate more points or to re-do the IRC calculating the force constants at every step. The first is the quickest, the second is slightly more reliable, but there is no guarantee that the number of steps chosen will be enough and the third is the most reliable but will take a large amount of computational time. The first method was chosen here due to time constraints. The structure produced by this optimization was very similar to the inputted structure and it is very possible that this structure is not the true minimum (the log file was checked and the force constants do not seem to have been calculated at all and so it is difficult to know if the structure had converged.) If more time were available it would have been beneficial to complete all of the above methods as this would have given an interesting comparison.
Calculating the activation energy of the reaction
The reaction energy of the reaction has to be calculated via both transition states, but firstly it is necessary to re-optimize both transition state structure to a higher level of theory (in this case the B3LYP and 6-31G* method and basis set). The structures that had been optimized to the 3-21G level were used as a starting point in order to save computational time. Both optimized transition states are shown below.
| The optimized chair transition state | The optimized boat transition state | ||||||
|
|
The energies of each structure were collated and are summarized in the table below. The activation energies are very close to those given in the lab manual (the activation energy via the chair transition state is given as 33.5 with a margin of 0.5 kcal/mol and the activation energy via the boat transition state is given as 44.7 with a margin of 2 kcal/mol).
| Structure | Energy calculated at the HF/3-21G level (kcal/mol) | Energy calculated at the B3LYP/6-31G* level, 0K (kcal/mol) | Energy calculated at the B3LYP/6-31G* level, 298.15K (kcal/mol) | Difference in calculated EA of rxn (kcal/mol) |
| Reactant | -145389.151 | -147131.5182 | -147220.963 | - |
| Chair transition state | -145343.2093 | -147097.4745 | -147186.6178 | - |
| Boat transition state | -145332.8425 | -147089.578 | -147177.9018 | - |
| Activation energy via the chair t.s. | 45.94169092 | 34.04361827 | 34.34516772 | 11.5965232 |
| Activation energy via the boat t.s. | 56.3085161 | 41.94019152 | 43.06123635 | 13.24727975 |
Information about the energies and enthalpies of the transition states at different temperatures can found in the log file under thermochemistry. The sum of electronic and zero point energies is the energy at OK including the vibrational energy and the other energies and enthalpies are at 298K.
The chair transition state:
Sum of electronic and zero-point Energies= -234.414924 Sum of electronic and thermal Energies= -234.409004 Sum of electronic and thermal Enthalpies= -234.408060 Sum of electronic and thermal Free Energies= -234.443808
The boat transition state:
Sum of electronic and zero-point Energies= -234.402340 Sum of electronic and thermal Energies= -234.396006 Sum of electronic and thermal Enthalpies= -234.395062 Sum of electronic and thermal Free Energies= -234.431094
The effect that these corrections have on the final activation energy of the reaction is shown in the table above. The predicted activation energy via the chair transition state is closer when the energy taken is that predicted for 0K, but the experimental value for the reaction via the boat transition state is closer to that predicted at room temperature. It can also be seen that the HF/3-21G basis set is much less reliable than the B3LYP/6-31G* method, as the energies predicted with the former method are around 10 kcal/mol out.
The Diels Alder Reaction
The Diels-Alder reaction is another example of a pericylic reaction whose transition state can be modelled. The most basic example of a Diels Alder reaction (between cis-butadiene and ethylene) will be considered first followed by the reaction of cyclohexadiene with maleic anhydride. Both will be considered in terms of orbital overlap and the latter will be considered in terms of the stereoselectivity of the reaction (i.e. whether the endo or the exo product will be formed).
The reaction of cis-butadiene and ethylene
Cis-butadiene was modelled and optmized using the semi-empirical level of theory (AM1). This optimized structure was then used to vizualize the molecular orbitals. The HOMO and LUMO of butadiene are shown below.
| The HOMO of butadiene | The LUMO of butadiene |
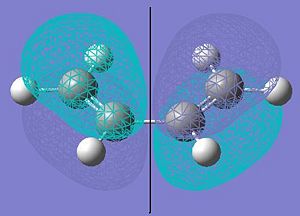
|

|
It can be seen that the HOMO of cis butadiene is antisymmetric with respect to the plane shown on the diagram and the LUMO is symmetric with respect to the same plane. A guessed structure for the transition state of the reaction was then made. This was done first by building a bicylco-octane type molecule, removing the bottom CH2-CH2 fragment and changing the distance between the carbons that form the bonds in the reaction. These bonds were set to 1.56 angstroms at first, as the average sp3-sp3 carbon-carbon bond is around this length. However, this was clearly not close enough to the transition state as the negative vibration shown by this structure did not correspond to the motion of the transition state of this reaction. The bond was then set to 2.2 angstroms, as this was the bond length in the transition state above. This input molecule is shown below.
Guessed transition state for the reaction of cis-butadiene and ethylene |
This molecule produced an output structure with one negative vibration, but this negative vibration did not correspond to the correct vibration (it was more of a methyl bend).
Since this method did not seem to work the next step was to try a different one. This time the reactants were put together in a geometry that was guessed to be near the transition state (see the molecule below.) The frozen bond method was used (the bonds that are made in the transition state) were frozen and set to 2.2 angstroms long. The rest of the structure was then optimized to a minimum. The frozen bonds were unfrozen and set to derivative and the structure was re-optimized to a transition state. The outputted structure is shown below (the file shown below is the log file, the checkpoint file did not have a partial double bond across the central C-C bond in cis-butadiene).
Transition state for the reaction of cis-butadiene and ethylene |
The bond lengths of the semi-formed bonds in this transition state structure were 2.2 Å long. The angle between the two fragments (i.e. the angle of attack) was optimized to be 101.603 degrees. The imaginary frequency (at -817.695 cm-1) this time corresponded to the correct vibration. This is shown in the picture below. The energy of the transition state was -231.60320841 hartree.
| The vibration of the transition state | The HOMO of the transition state | The LUMO of the transition state |
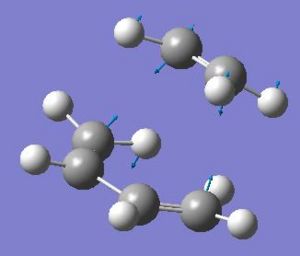
|

|

|
The HOMO and LUMO of the transition state were visualized; the HOMO was found to be symmetric with respect to the plane shown on the diagram with 3 nodal planes. The LUMO was also found to be symmetric about the plane shown but had 4 nodal planes. The structure of these orbitals (the positions of the nodal planes in particular) suggests that they were formed from the p-orbitals of each reactant.
The reaction of cyclohexadiene and maleic anyhdride
The reaction between cyclohexadiene and maleic anhydride can have two possible outcomes; the product can either be endo or exo. Which of these two products is formed is dependant on which way the two reactants approach each other in the transition state. If maleic anhydride approaches cyclohexene with the hydrogens pointing over the two double bonds then the exo product is formed. If maleic anhydride approaches with the hydrogens pointing away from the double bond then the endo product is formed (see the reaction scheme below). All optimizations were run to the HF/3-21G level in order to save computational time.
The exo transition state was modelled first using the frozen bond method. The two reactant molecules were drawn in ChemBio3D, opened in GaussView and then copied into the same file. The carbons that form the new bonds were set to 2.2 angstroms apart when frozen. However on completing a vibrational analysis it was clear that this guess had not produced the correct transition state, as the negative vibration (at -78.7927 cm-1) corresponded to a methyl wiggle rather than the bond forming carbons becoming closer. The input molecule used for this optimization is shown below.
Input molecule for the transition state of the reaction between maleic anhydride and cyclohexadiene |
The frozen bond lengths were next set to 2.4 angstroms. This gave the correct transition state; the negative vibration was at -647.387 cm-1 and corresponded to the forming of two new bonds as would have been expected. The energy of the exo transition state was -605.60359123 hartree.
| Optimized exo transition state | The negative vibration of the exo transition state | |||
|
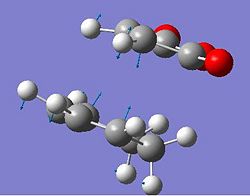
|
The HOMO and LUMO of the exo transition state were visualized and are shown below. It is possible to see from these pictures, the favourable interactions that cause the product to form from this transition state. There are two orbital interactions in the HOMO of the transition state. This can be predicted on paper (secondary orbital overlap), and this is discussed in the section on orbital overlap below.
| The HOMO of the endo transition state | The LUMO of the endo transition state |

|
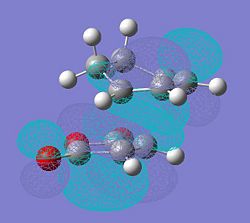
|
The endo transition state was then optimized using the frozen vond method (the bonds were frozen to 2.2 angstroms). The ouptut geometry is shown below. This one showed a negative vibration at -647.845 cm-1 that corresponds to the expected vibration of the transition state (the bond forming carbon atoms are stretching towards one another). This vibration was at -647.845 cm-1.
| Final optimization geometry of the endo transition state | The negative vibration of the endo transition state | |||
|---|---|---|---|---|
|

|
The energy of the optimized endo transition state was -605.60359125 hartree. The HOMO and LUMO of the endo transition state were also visualized (shown below). These can be compared very well with those predicted by secondary orbital overlap theory (see the section below.)
| The HOMO of the endo transition state | The LUMO of the endo transition state |

|

|
Orbital overlap
The energy of the endo transition state is found to be higher than that of the exo transition state (The exo transition state had an energy of -605.60359123 hartree whereas the endo state had an energy of -605.60359125 hartree) which corresponds to an energy difference of 0.00001255 kcal/mol. This is qualitatively unsuprising, as there are more favourable orbital overlaps available when the molecules approach in the endo transition state (there are overlaps available in the endo transition state and 2 available in the exo transition state). These orbital interactions are known as secondary orbital interactions, and are shown below. However, it is slightly quantitatively suprising as the energy difference is very small and would not be expected to make any practical difference.
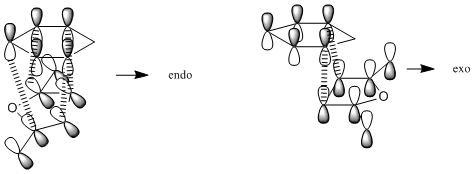
The orbital overlaps that we expect can also be seen in those computed for the transition states. Comparing the drawn secondary orbitals interactions to the computed HOMOs of each transition state we can see the corresponding pi clouds around which the reactivity is based.
References
- The exercise guidelines [1]
- Clayden, Greeves, Warren and Worthers Oragnic Chemistry pgs 906, 910, 914 - 922 (Chapter 35)
