Rep:Finalmod

Introduction

During this investigation the transition structures on potential energy surfaces for the Cope rearrangement and Diels Alder cycloaddition reactions will be characterised. The main aim is to demonstrate the power of high-level quantum computations in offering insights towards understanding the nature of organic molecules- their structures, properties and reactions- and to emphasise their usefulness, whilst pointing out some potential pitfalls of these calculations.

Molecular Modeling

Prior to the 1960s, organic reactivity was thought to be dominated by factors which included:

• The relative stability of reactant and product (i.e. thermodynamic control)
• Geometrical effects such as strain, steric interactions, hydrogen bonding, neighbouring group effects (entropy),
• Electrostatic effects such as the polarity of functional groups (eg the carbonyl group) and the aromaticity of either the reactant or the product.

During the course of the synthesis of vitamin B12 in the early 1960s, Robert Woodward concluded that none of the above factors could rationalise several experimental observations. A new explanation was developed based on 'stereoelectronic' factors, i.e. recognising that the three-dimensional properties of the electrons and their phase relationship could dominate the other factors listed above. This theory of stereoelectronic control of pericyclic reactions was derived using an approach known as the conservation of orbital symmetry, together with the theoretician Roald Hoffmann.

The Nobel prize winner, John Pople, was recognized for developing the Gaussian program, one of the best known of the molecular modelling systems, and one which has been crucial in quantifying aromaticity and creating accurate models of reaction transition states and potential energy surfaces. This program will be used for each calculation.

Pericyclic Reactions

A pericyclic reaction is one in which bonds are made or broken in a concerted cyclic transition state. A concerted reaction is one which involves no intermediates during the course of the reaction (left). A stepwise and therefore non-concerted and non-pericyclic reaction is shown with a discrete intermediate (right).

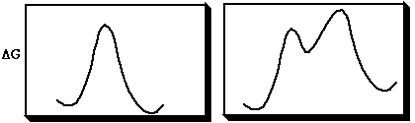
Understanding pericyclic reactions therefore involves understanding the transition states that control them. Pericyclic reactions have certain characteristic properties, three of which are:

• There is no nucleophilic or electrophilic component. This means that in the arrow pushing sense, there is no beginning and no ending for the arrows, and the arrow pushing can occur in either a clockwise or anti-clockwise direction.
• Pericyclic reactions can be frequently promoted by light as well as heat. Normally, the stereochemistry under the two sets of conditions is different and it was (originally) thought invariably opposite. Current thinking about the photochemical route is more complex.
• Pericyclic reactions normally show a very high stereospecificity.

Part 1- Cope Rearrangement

Sigmatropic reactions are one class of pericyclic reactions. A sigmatropic reaction involves the concerted migration of an atom or group of atoms from one point of attachment to a conjugated system to another point of attachment, during which one σ bond is broken and one σ bond is formed.

The Cope rearrangement is perhaps the premier example of [3,3]-sigmatropic rearrangements. It is accurately denoted as a (3,3)-sigmatropic reaction as the σ bond formed is three carbon atoms away from the σ bond which is broken. This is shown below.

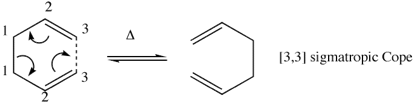
Although first discovered in the 1940s, the mechanism of this reaction remained controversial well into the 1990s. Nowadays it is generally accepted that the reaction occurs in a concerted fashion via either a "chair" or a "boat" transition structure, with the "boat" transition structure lying several kcal/mol higher in energy. The B3LYP/6-31G* level of theory has been shown to give activation energies and enthalpies in remarkably good agreement with experiment. In this tutorial it will be demonstrated how Gaussian can be use to calculate these values.

Optimising the Reactants and Products

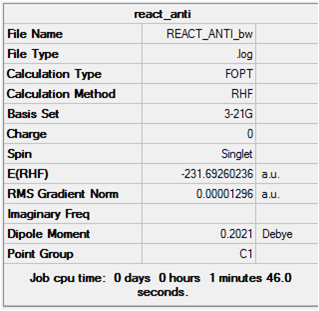
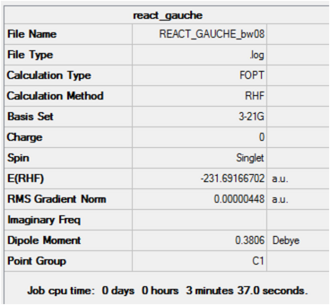
Using GaussView, a molecule of 1,5-hexadiene was drawn with an "anti" linkage for the central four atoms and the structure cleaned using the Clean function under the Edit menu. The HF/3-21G level of theory was used to optimise the structure. The same procedure was carried out for the conformation with a "gauche" linkage and the results are summarised below. Input Files

Media:React anti bw.gjf

Media:React gauchebw08.gjf

Output Files

Media:REACT ANTI bw.LOG

Media:REACT GAUCHE bw08.LOG

Anti

The energy of this conformer lies closest to that of anti1 shown in Appendix 1. Symmetrising resulted in an output of C₂, agreeing with that of anti1.

Gauche

This structure is almost identical in energy to gauche2 shown in Appendix 1. Symmetrising resulted in an output of C₂, agreeing with that of gauche2.

Comparisons

From the results above the anti conformer is approximately 0.59 kcal/mol lower in energy than the gauche conformer. The anti conformer is expected to have a lower total energy due to the fact that there is likely to be a larger degree of orbital overlap between the C/C-H σ-orbital and the C-C/C-H σ*-orbitals in the anti conformer as the orbitals are more effectively aligned for interaction. A diagram illustrating the origin of this stabilisation concept is shown below.

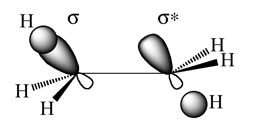
A range of conformations were then trialled by varying the dihedral angle of the central four carbon atoms and by changing the C-C-H angle in certain cases where stabilisation was to be expected. Four of the conformations have been compared in detail, as shown in the table below.

Energy and point groups of four conformers explored

	anti1	anti3	gauche4	gauche1
Jmol
Energy/ au	-231.69225	-231.68906	-231.69155	-231.68779
Energy/ kcal/mol	0.04	2.25	0.71	3.10
Point group	C2	C2h	C2	C1

Additionally, there is a van der Waals attraction when the H^..H distance is 2.4 Å and in gauche4 it is 2.49 Å , and increases to 2.54 Å for gauche1, as does the energy. The conformer gauche3 has the distance closest to this van der Waals attraction at 2.41 Å, helping to explain why this conformer was found to have the lowest energy of all structures. This distance was measured for anti 1 to be 2.51 Å for anti 3 2.50 Å. This helps to explain the relative stabilisation and smaller energy differences between the gauche and anti conformers than initially expected.

Analysis of the natural bonding orbitals of each conformer also yielded interesting information which helps to explain relative stabilities. The HOMO of the anti1 and gauche1 conformers are shown below.

NBO analysis: HOMO orbitals

	anti 1	gauche 1
MO (HOMO)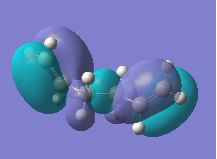
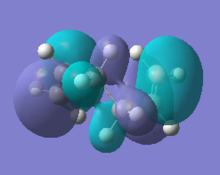
MO energy (au)	-0.350	-0.348

Firstly, the energy of the HOMO for anti1 is lower than that of gauche1, which is consistent with the anti conformer being lower in total energy. From the figures above it is clear that there is a lower degree of anti-bonding character in the NBO of the anti conformer compared to that of the gauche conformer. The orbitals of the anti conformer are more closely aligned to 180°, which is most effective for stabilsation effects outlined above, therefore contributing to the slightly lower total energy of this conformer.

Optimisation of C_i conformer with HF and DFT methods

The C_i anti2 conformation of 1,5-hexadiene was drawn and optimised using the HF/3-21G level of theory. Its symmetry was confirmed as C_i. The energy of this conformer was just 0.006 kcal/mol higher than that of the corresponding conformer shown in Appendix 1. This structure was then reoptimized at the B3LYP/6-31G* level. The results are shown below.

Input Files

Media:REACT Ci DFTFinal.gjf

Media:REACT Ci DFTFinal freq.gjf

Output Files

Media:REACT CI DFTFINAL.LOG

Media:REACT CI DFTFINAL FREQ.LOG

The greater level of theory used during the B3LYP/6-31G(d) calculation results in a reduction of the total energy of the conformer by approximately 3 a.u.

C_i conformer optimisations

	HF/3-21G	B3LYP/6-31G(d)
Jmol
Energy/ au	-231.69253	-234.55970
Point group / kcal/mol	Ci	Ci

The DFT method clearly results in a much lower energy conformation, but initial comparison of both structures indicates very little difference in both conformers. Further analysis was then completed, as shown below.

C_i conformer bond lengths

Bond lenghts/Å	HF/3-21G	B3LYP/6-31G(d)	Literature
C1-C2	1.32	1.33	1.34
C2-C3	1.51	1.50	1.50
C3-C4	1.55	1.55	1.54
C4-C5	1.51	1.50	-
C5-C6	1.32	1.33	-

C_i conformer dihedral angle/^o

	HF/3-21G	B3LYP/6-31G(d)
C1-C2-C3-C4	114.5	118.9
C2-C3-C4-C5	179.9	180.7
C3-C4-C5-C6	-115.8	-118.4

Comparison of dihedral angles shows that the C₂-C₃-C₄-C₅ is closer to the optimal 180^o for optimal overlap, but the difference is small. Furthermore, the bond lengths are similar for each structure.

Overall it can be said that the DFT method has not changed the geometry considerably in comparison to the HF method as the point group has also been retained. In total, the geometries have not changed greatly, but the greater level of computational power of the DFT method results in a lower energy primarily due to a large number of small changes in various parameters such as bond lengths and angles.

Overall, the B3LYP/6-31G(d) method produces data which is in better agreement with literature values, although in this case the deviation from literature value is relatively small for both structures. This emphasises the value of HF/3-21G calculations when the system involved is composed of a relatively low number of atoms such as carbon and hydrogen. It took approximately two minutes longer for the B3LYP/6-31G(d) calculation to complete, although the data obtained was slightly more accurate. This balance between longer computational time involving the use of more complex techniques must be balanced with the improvement of end result compared to experimental values.

Frequency Calculation

Vibrational analysis of the conformer produced from the B3LYP/6-31G(d) calculation confirmed that the structure was at a minimum as there were no negative frequencies obtained, as shown in the log file above and the spectrum below.

Two of the most useful absorptions for identification of alkenes is the high frequency C-H stretching modes and the C=C stretches, two of which are shown below.

Exo/Endo orbital effects

Assigned Vibration	Frequency/cm-1	Animation
Alkene C-H stretch	3244
C=C stretch	1728

Analysis of Output File

Notice that in the .log output file we observe 6 "low frequencies" which are not classified as "real" vibrational frequencies as they correspond the the 3 degrees of freedom in translational and rotational motion.

We can also extract vital information regarding the different types of energy of the molecule to enable comparison to the appropriate energy in the literature:

(i) "The sum of electronic and zero-point energies" corresponds to the potential energy at 0K + Zero pt. energy

(ii) "The sum of electronic and thermal energies" corresponds to the energy (1atm, 298.15K) inc. translational, vibrational and rotational contributions

(iii) "The sum of electronic and thermal enthalpies" effectively includes RT correction

(iv) "The sum of electronic and thermal free energies" is an effective freee energy, G = H - TS

These values at 298 K and 0.001 K were computed and are shown below.

Energy Type	298.15 K and 1 atm	0 K and 1 atm
Sum of electronic and zero-point energies	-234.416245	-234.469203
Sum of electronic and thermal free energies	-234.408955	-234.461855
Sum of electronic and thermal enthalpies	-234.408011	-234.4507613
Sum of electronic and thermal free energies	-234.447848	-234.470121

This information will be useful in subsequent calculations.

Cope Transition State

In this section the transition structure optimization will be set up and completed using three methods- (i) by computing the force constants at the beginning of the calculation, (ii) using the redundant coordinate editor, and (iii) using QST2. The reaction coordinate will be visualized and the IRC (Intrinisic Reaction Coordinate) run. The information produced will be used to calculate the activation energies for the Cope rearrangement via the "chair" and "boat" transition structures.

Chair

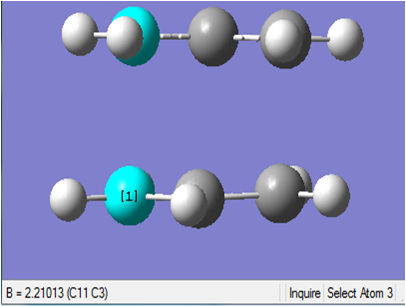
An allyl fragment was drawn and optimized using the HF/3-21G level of theory. After opening a new window in GaussView the optimised allyl fragment was copied into this and a second molecule was appended into the same window. Both fragments were arranged so that the distance between the terminal ends of the allyl fragments was approximately 2.2 Å as shown below.

A Gaussian optimization for a transition state was then set up by selecting the job type as Opt+Freq and then changing the Optimization to a Minimum to Optimization to a TS (Berny). Force constants were chosen to be calculated once and the final modification to the input file was to type Opt=NoEigen in the Additional keyword box. The files for the optimisation are shown below.

Input FilesMedia:Optimisationallyl opt-3-21.gjf Output Files Media:GUESS-TS.LOG

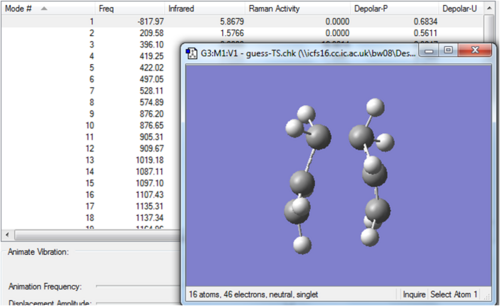
The frequency calculation gave an imaginary frequency of magnitude 818 cm^-1. This vibration is animated below and clearly corresponds to the Cope rearrangement due to the concerted fashion in which one σ-bond is breaking and one σ-bond is forming.

The chair transition structure was then optimised using the frozen coordinate method. The coordinate editor was used and Bond instead of Unidentified was selected, then Freeze Coordinate instead of Add was selected once the terminal carbon atoms had been highlighted. This was done for both termini, setting the length to 2.2 Å. Input File Media:Mod Redundant.chk Output File Media:MOD REDUNDANT.LOG The outputted geometry looked very similar to that optimised previously but this time the terminal C-C bond lengths were both equal to 2.2 Å.

The terminal C-C bond lengths were then optimised. This was done by opening the Redundant Coordinate Editor and choosing Bond instead of Unidentified and Derivative instead of Add, for each terminal C-C bond. This time the transition state optimization was set up but force constants were not calculated as done so previously, instead a normal guess Hessian was used, modified to include the information about the two coordinates we are differentiating along. The output file was used to perform a frequency calculation, the resulting imaginary frequency is shown below.

Input Files Media:Mod Redundant2.chk Media:MOD REDUNDANT2bwfreq.gjf

Output Files Media:MOD REDUNDANT2bw.LOG Media:MOD REDUNDANT2BWFREQ.LOG

The imaginary frequency calculated using this method is just 0.18 cm^-1 less negative than that calculated during the previous step. Again, the imaginary frequency corresponds to the Cope rearrangement due to the concerted fashion in which one σ-bond between the two termini is breaking and another σ-bond is forming. The geometry of the optimised transition structure is shown below.

Chair following freeze

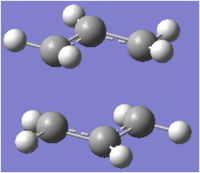
The final energies for the chair transition state were -231.6193224 a.u. and -231.6193219 a.u. when using the first method and the frozen coordinate method respectively. Terminal C-C bond lengths were found to be the same. As there is an error associated with both calculations it can be concluded that the results from both techniques are identical.

HF output:

Sum of electronic and zero-point Energies= -231.466700

Sum of electronic and thermal Energies= -231.461340

Sum of electronic and thermal Enthalpies= -231.460396

Sum of electronic and thermal Free Energies= -231.495206

Boat Transition State

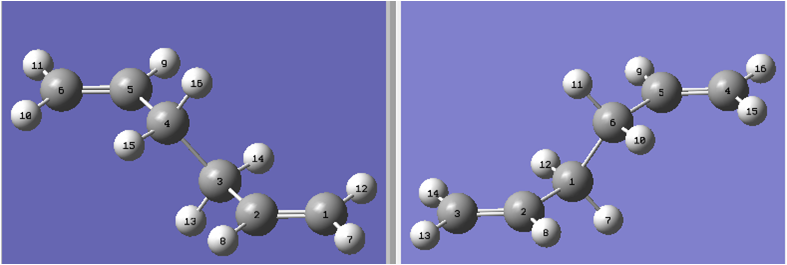
Now the boat transition structure will be optimized. This was completed using the QST2 method. In this method, the reactants and products for a reaction are specified and the calculation interpolates between the two structures to try to find the transition state between them. To ensure a successful computation, the reactants and products must be numbered in the same way. Hence the atom numbering must be manually changed the numbering for the product molecule so that it corresponds to the numbering obtained if the reactant had rearranged.

With the current starting geometries the job fails (shown below). The output resembles the chair transition structure but more dissociated. When the calculation linearly interpolated between the two structures, it simply translated the top allyl fragment and did not consider the possibility of a rotation around the central bonds. It is clear that the QST2 method will not locate the boat transition structure starting from these reactant and product structures. Input File Media:Failed.gjf Output File Media:FAILED.LOG

Hence the original input file for the QST2 calculation was used to modify the reactant and product geometries so that they are closer to the boat transition structure. The central C-C-C-C dihedral angle (i.e. C2-C3-C4-C5 for the molecule above) was changed to 0°. and the side C-C-C (i.e. C2-C3-C4 and C3-C4-C5 for the molecule above) was reduced them to 100°. The same was done for the product molecule. The reactant and product molecules then looked like the following:

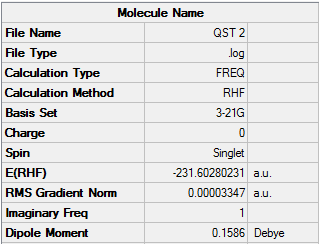
This time the job is successful and the geometry converges to the boat transition structure. There is only one imaginary frequency which can be visualized below.

IMAGINARY FREQUENCY QST 2

This illustrates that although the QST2 method is has some advantages because it is fully automated, it can often fail if the reactants and products are not close to the transition structure.

Input Files Media:2nd boat attempt 1.gjf Media:QST 2.gjf

Output Files Media:2ND BOAT ATTEMPT 1.LOG Media:QST 2.LOG

Sum of electronic and zero-point Energies= -231.450924

Sum of electronic and thermal Energies= -231.445297

Sum of electronic and thermal Enthalpies= -231.444353

Sum of electronic and thermal Free Energies= -231.47976

Intrinsic Reaction Coordinate

Take a look at your optimized chair and boat transition structures. Which conformers of 1,5-hexadiene do you think they connect? You will find that it is almost impossible to predict which conformer the reaction paths from the transitions structures will lead to. However, there is a method implemented in Gaussian which allows you to follow the minimum energy path from a transition structure down to its local minimum on a potential energy surface. This is called the Intrinisic Reaction Coordinate or IRC method. This creates a series of points by taking small geometry steps in the direction where the gradient or slope of the energy surface is steepest.

It is difficult to predict which conformers of 1,5-hexadiene the two transition structures connect from simple observations. The Intrinsic Reaction Coordinate implemented within Gaussian allows the minimum energy path from a transition structure to its local minimum to be followed. This creates a series of points by taking small geometry steps in the direction where the gradient or slope of the energy surface is steepest.

Chair

The optimized chair structure was used to carry out an IRC calculation, setting the calculation in the forwards direction only as the coordinate is symmetrical, calculating force constants once and to consider 50 points along the reaction coordinate. The result is shown below.

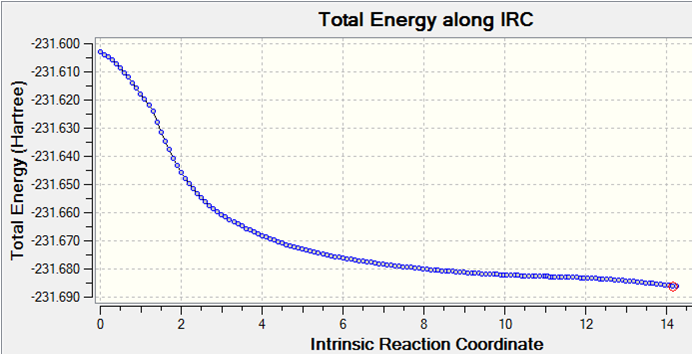
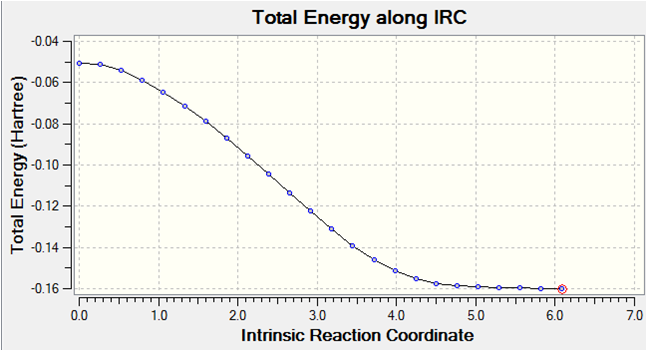
It is clear that a minimum geometry was not yet reached during this computation. By increasing the number of steps to 150, reducing the stepsize to 5 and calculating force constants at every step the minimum energy structure was reached as shown below. DOI:10042/to-8022

The IRC converges to -231.69106 a.u. which is closest in energy to the gauche2 structure. Symmetrizing the product resulted in a structure having C₂ symmetry, which is the same as gauche2. The conformation looks almost identical to this structure and a final optimisation using HF/3-21G results in an energy which is the same as that shown in Appendix 2.

Boat

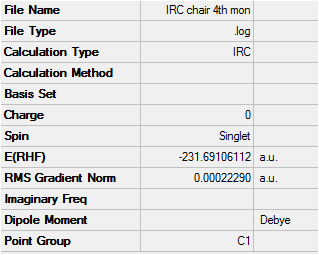
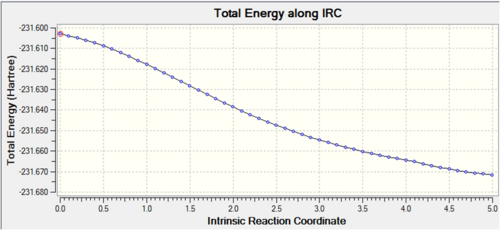
An IRC calculation was then completed on the optimized boat transition structure, setting the constraints to the same as those done for the initial chair transition state optimisation. The result is shown below. Input FilesMedia:IRC boat.gjf Output FilesDOI:10042/to-7996

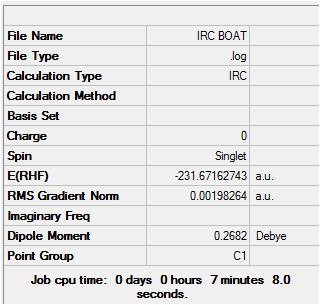
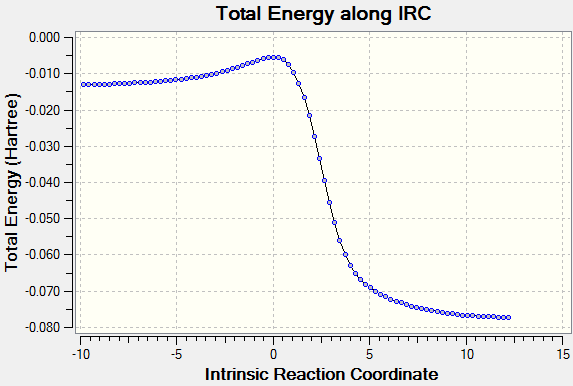
Once again, from the first optimisation it is clear that a minimum geometry had not yet been reached. By increasing the number of steps to 150, reducing the stepsize to 5 and calculating force constants at every step the minimum energy structure was reached as shown below. Input File Media:IRC boat final.gjf Output File (could not upload)

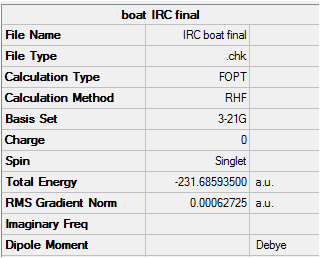
The IRC converges to -231.69106 a.u. which is very close in energy to that of the gauche3 structure. Symmetrizing the product resulted in a structure still having C₁ symmetry, which is the same as that of gauche3. The conformation looks almost identical to this structure and a final optimisation using HF/3-21G results in an energy which is just 0.0003 a.u. higher than the structure in Appendix 2.

DFT and HF Activation Energy Comparisons

Finally the activation energies for both transition structures were calculated. The chair and boat transition structures were reoptimized using the B3LYP/6-31G* level of theory before carrying out frequency calculations. In each case the starting structure was the HF/3-21G optimized structure. The results are summarised below.

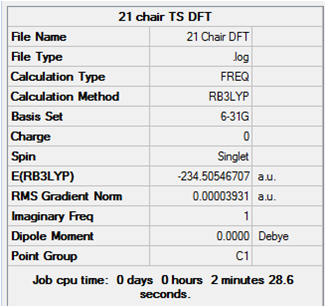
Chair

Input File

Media:21 chair TS DFT.gjf

Output File

Media:21 Chair DFT.out

Sum of electronic and zero-point Energies= -234.362663

Sum of electronic and thermal Energies= -234.356753

Sum of electronic and thermal Enthalpies= -234.355809

Sum of electronic and thermal Free Energies= -234.391587

The B3LYP/6-31G* optimisation lowered the energy of the chair transition state by approximately 2.9 a.u., although the geometry for both optimisations are very similar, but the terminal C-C bond length is 0.08 Å shorter after optimisation at the higher level, which is likely to contribute to the lower total energy.

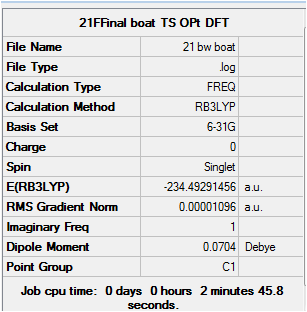
Boat

Input File

Media:21FFinal boat TS opt DFT.gjf

Output File

Media:21 bw boat.out

Sum of electronic and zero-point Energies= -234.351356

Sum of electronic and thermal Energies= -234.345053

Sum of electronic and thermal Enthalpies= -234.344109

Sum of electronic and thermal Free Energies= -234.380776

The geometries were found to be similar for both structures as the angles and bond lengths were very close in each method. The DFT method gives transition structures which have a shorter terminal C-C bond for the chair (1.97 Å) compared to the boat (2.21 Å). This may indicate a stronger force of attraction in this transition state, contributing to the lower energy of the chair transition structure. Additionally, the C-C-C bond angle is closer to 120° in the chair transition structure (119.95°) than in the boat transition state (12.25°). The fact that this angle is closer to the ideal 120° of an sp² hybridised carbon atom in the chair transition structure also helps to explain why there is less strain in this transition state. (The energy summary is provided below.)

Summary of energies (in hartree)

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619322	-231.466700	-231.461340	-234.505467	-234.362663	-234.356753
Boat TS	-231.602802	-231.450924	-231.445297	-234.492915	-234.351356	-234.345053
Reactant (anti2)	-231.692535	-231.539539	-231.532566	-234.556983	-234.414476	-234.407129

Summary of activation energies (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.71	44.69	32.51	31.6	33.5 ± 0.5
ΔE (Boat)	55.61	50.43	39.61	48.65	44.7 ± 2.0

The computed activation energies of the chair and boat transition structures, using both methods, agree with the experimental values. The HF/3-21G method results in an overestimation of the activation energy. Further optimisation using the B3LYP/6-31G* method clearly resulted in a result which is closer to the experimentally observed activation energy values.

Further Discussion

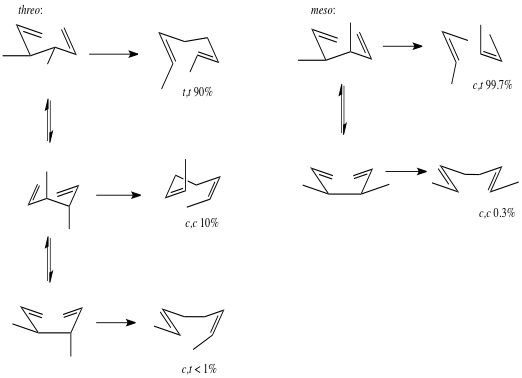
The classic Doering and Roth experiment addressed the stereochemistry of the Cope rearrangement. Heating threo- or meso-3,4-dimethyl-1,5-headiene gives mixtures of octadienes that indicate a preference for the reaction to occur through a chair-like transition state. They estimated that the chair pathway was preffered over the boat pathway by at least 5.7 kcalmol^-1 in free energy, a figure later supported by Goldstein’s experiments with deuterated 1,5-hexadiene.

More contentious has been the nature of the mechanism itself. Outlined below are the three main limiting cases for the mechanism. The reaction can proceed along a concerted path, passing through a single transition state (1a) with no intermediates (path a). This transition state invokes delocalization across all six carbon centres and has been termed an “aromatic” transition (4n+2 electrons).

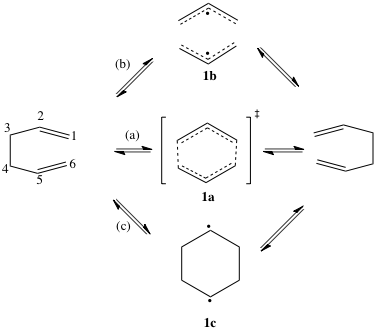
There are two stepwise possibilities. Following path (b), the σ (C3-C4) as labelled) bond is cleaved first, creating two non-interacting allyl radical species (1b). The ends of these allyl radicals can then combine to give product. The alternative is path (c), where the bond between the two carbon atoms labeled 1 above forms first, creating cyclohexane-1,4-diyl (1c) as a stable intermediate. Cleaving the 3-4 bond then forms the product.

The experimental activation enthalpy for the Cope rearrangement of 1,5-hexadiene is 33.5 kcal mol^-1.

The cleavage pathway (path b) has been discounted for two reasons. First, the estimate for the dissociation energy of 1,5-hexadiene into two allyl radicals is 59.7 kcal mol^-1, which is much higher than the activation barrier. Secondly, experiments indicate no crossover products, which would be expected if allyl fragments were liberated.

Doering et al. estimated that cyclohexane-1,4-diyl would be 33.7 kcal mol^-1 higher in energy than 1,5-hexadiene, essentially identical to the activation barrier, championing path (c). However, they used a faulty estimate for the bond dissociation energy for forming the iso-propyl radical from propane. With current group equivalents and bond energies, the diyl is estimated to be 42 kcal mol^-1 higher in energy than 1,5-hexadiene, suggesting that it too is unlikely to participate in the Cope rearrangement. This set up the environment in which computational chemists came to weigh in on the nature of the Cope rearrangement.

Density functional theory, for example, has been applied to the Cope rearrangement. Nonlocal methods find a single transition state with R₁₆ approximately 2Å. The barrier height is in excellent agreement with experiment. Computation on a CCSD surface also indicates a single minimum on the C_2h slice, corresponding to an aromatic transition state and agreeing that path (a) is the actual mechanism.

Important Experimental Results

Based on Goldstein’s studies of the Cope rearrangement of the 1,5-hexadienes, the chair transition state is estimated to be 11.3 kcal/mol lower in enthalpy than the boat transition state. Shea and Phillips designed the diastereomeric pair 2c and 2b, which can undergo a Cope rearrangement exclusively through a chair transition state or a boat transition state, respectively.

Consistent with Goldstein’s results, the activation enthalpy for the Cope rearrangement of 2c is 13.8 kcal/mol lower in energy than that of 2b. Dolbier followed these experiments with a study of the difluoronated analogs 3b and 3c. The activation enthalpy for the Cope rearrangement of 3c is 5.6 kcal/mol below that of 2c, but the barrier for reaction of 3b is 7.9 kcal/mol above that for 2b.

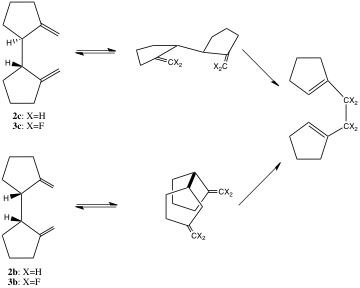
Perhaps even more intriguing are the experimental activation entropies: -11.3 and -17.5 eu for 2c and 3c, respectively, which are in the range of typical values. But the activation entropies for 2b and 3b are -0.7 eu and +8.7 eu respectively. The more positive activation entropies of the boat than the chair paths suggest more bond breaking than bond forming in the former. The very positive activation entropy for 3b suggests there is essentially no bond making, only bond breaking in this boat transition state. As Dolbier noted, “This (the reaction of 3b) is a Cope rearrangement which does not want to be pericyclic."

Part 2 - The Diels Alder Cycloaddition

During this exercise the transition structures of two cycloaddition reactions will be characterised. By analysing the molecular orbitals involved, key directing effects will be explained.

A cycloaddition reaction involves the concerted formation of two or more σ bonds between the termini of two or more conjugated π systems. The reverse reaction involves the concerted cleavage of two or more σ bonds to produced two or more conjugated π systems.

The most common example is the Diels Alder cycloaddition. Two π systems are involved, one contributing 4π electrons, the other 2π electrons. The total electron count is 6 (4n+2, n=1) and since the reaction is thermal, it must proceed via Huckel topology involving only suprafacial components.

Prototype Reaction

This reaction study involves the cycloaddition between ethane and butadiene. Many Organic Chemistry textbooks contain this reaction as the basic Diels Alder reaction. Yet in most cases the Diels-Alder reaction involves a dienophile that is conjugated with an electron withdrawing group (as shown in the next example).

Input Files Media:Ethene opt 1.gjf Media:Cis buta opt.gjf Output Files Media:ETHENE OPT 1.LOG Media:CIS BUTA OPT.LOG

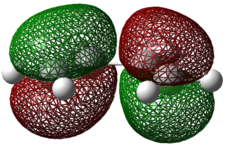
The AM1 semi-empirical molecular-orbital method was used to optimise both compounds and the key interacting molecular orbitals are shown below.

AM1 optimisation - HOMO-LUMO Comparison of Cis-butadiene and Ethylene

Ethene: HOMO: symmetric	Ethene: LUMO: antisymmetric	Cis butadiene: HOMO: antisymmetric	Cis butadiene: LUMO: symmetric

Each of these molecular orbitals is either symmetric (s) or antisymmetric (a) with respect to the plane of symmetry. This has been indicated above. Hence the HOMO of ethene and the LUMO of butadiene are both s and the LUMO of ethane and the HOMO of butadiene are both a. Hence as it is possible to pair up the HOMO of one molecule with the LUMO from the other by symmetry (i.e. both a or s) the reaction is allowed.

Computation of the Transition State Geometry for the Prototype Reaction and an Examination of the Nature of the Reaction Path

The optimized fragments shown above were arranged with initial separation between the terminal carbon atoms of approximately 2.0 Å. The semi-empirical AM1 method was initially used to locate the transition state, before the higher level DFT-B3YLP/6-321G* method and basis set was completed. The results are shown below. DOI:10042/to-8042

Summary TS (Berny)

Method	Structure	Animation	Frequency/cm-1
Semi-empirical AM1	Separation = 2.12 Å, C=C = 1.38 Å, C-C = 1.40 Å	Vibration	- 956
DFT-B3YLP/6-321g*	Separation = 2.27 Å, C=C = 1.38 Å, C-C = 1.41 Å	Vibration	- 524

The single imaginary frequency at -956cm^-1 for the semi-empirical AM1 method and -524cm^-1 for the DFT calulation shows that a transition state has been reached. The two σ bonds forming animated in each vibration above and comparison with the first positive frequency, which indicates an asynchronous twist which is not associated with the bonds forming during this reaction. If a transition state had been formed then we would expect the σ C-C forming bond length to lie in between the C-C length (1.54 Å) for an sp³ hybridised bond (in the product) and the sum of the van der Waals radii (3.14 Å) for two carbon atoms. This is observed as bond lengths of 2.12 Å for the AM1 method and 2.27 Å for the more experimentally accurate DFT method. From the bond lengths above there is clearly a difference between the single and double bonds in the fragments, indicating that we have an early transition state where the transition structure is “reactant-like”.

The fragment double bonds are approximately 1.40 Å which is longer than a sp² C=C alkene bond (1.33 Å), consistent with bond breaking. The central C-C single bond of the butadiene fragment is also approximately 1.40 Å, which is shorter than the observed C-C bond of 1.54 Å in alkanes, which is consistent with double bond formation.

HOMO-LUMOs Transition state

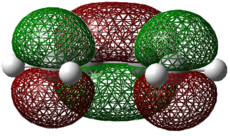
Method	HOMO	LUMO
Semi-empirical AM1	HOMO	LUMO
DFT-B3YLP/6-321g*	HOMO	LUMO

DFT-B3YLP/6-321g* optimisation: Further HOMO-LUMO Comparison in Transition State

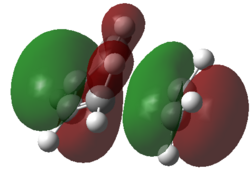Inspection of the a HOMO for the AM1 transition state indicates that the structure has formed by interaction of the a HOMO of cis-butadiene and a LUMO of ethylene. Analysis of the s LUMO indicates contributions from s LUMO of butadiene and the s HOMO of ethylene. The agreement in terms of orbital symmetry matching is consistent with the reaction being allowed.

Consideration of the DFT results yields some interesting information. For both the HOMO and LUMO their symmetries are s. Further analysis of the HOMO and LUMO of this transition state indicates contributions from the s HOMO of ethene in both cases. The LUMO of the transition has a large contribution from the s LUMO of butadiene. This results the reaction being classified as [π_2s+π_4s]. Yet neither the HOMO or LUMO of butadiene resemble the phase of the molecular orbital on the butadiene part of this transition state (although it seems symmetric), which can be attributed to the different ordering of the orbitals under the DFT method. This stresses the importance of the choice of method used and the care which must be taken when comparing results using two different methods.

It is important to bear in mind that the reaction above occurs in a very low yield due to the relatively unreactive dienophile of ethene. For example, reactions to combine even such a reactive diene as cyclopentadiene with a simple alkene lead instead to the dimerization of the diene. One molecule acts as the diene and the other as the dienophile to give the cage structure shown below.

However, the results during this section highlight the importance of orbital symmetry in determining whether a reaction is allowed, and the bond lengths measured are consistent with theory and experiment.

Regioselectivity of the Diels Alder Reaction Between Cyclohexa-1,3-diene and Maleic anhydride

Reaction of Cyclohexa-1,3-diene with maleic anhydride results in predominantly the endo product as shown below and this reaction proceeds in a high yield, for example due to the higher reactivity of the electron deficient dienophile as shown on the left. This reaction is a prime example of the regioselectivity of the Diels Alder reaction and during this section an explanation for the selectivity will be explained.

Indication of resonance contributions which place a δ+ charge on the dienophile, increasing its reactivity and the yield observed during this reaction.

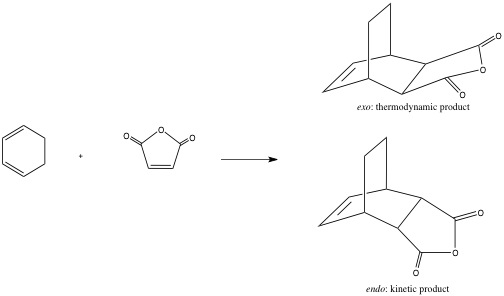
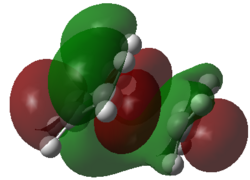
In order to explain why the endo compound predominates the product mixture and to understand why the transition state leading to the formation of this product is lower than that leading to the exo product the transition structures leading to the formation of both compounds must be determined and examined. Once again a semi-empirical AM1 method will be used due to its simplicity and effectiveness. The maleic anhydride fragment and then the cyclohexa-1,3-diene structures were optimised initially, followed by a range of transition state optimisations before the final successful result was produced. The results are shown below.

AM1 optimisation - HOMO-LUMO cyclohexadiene/maleic anhydride

HOMO cyclohexadiene	LUMO cyclohexadiene	HOMO maleic anhydride	LUMO maleic anhydride

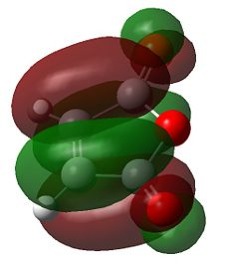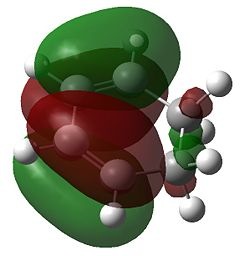
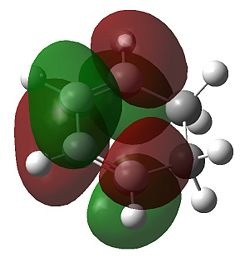
Hence as the HOMO of cyclohexadiene and the LUMO of maleic anhydride are both antisymmetric, the reaction is allowed as these orbitals can interact.

Exo/Endo transition states

Approach	Summary	Animation	Frequency/cm-1
Exo DOI:10042/to-8039			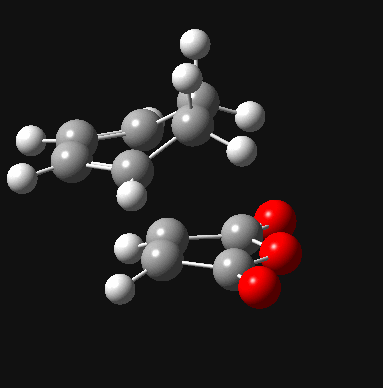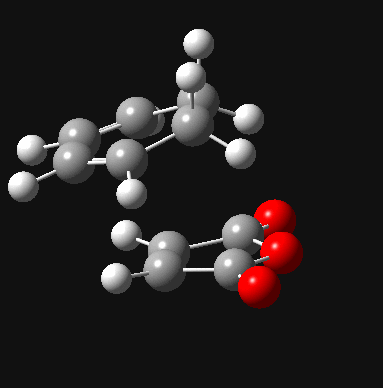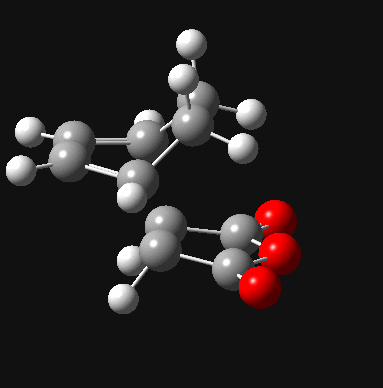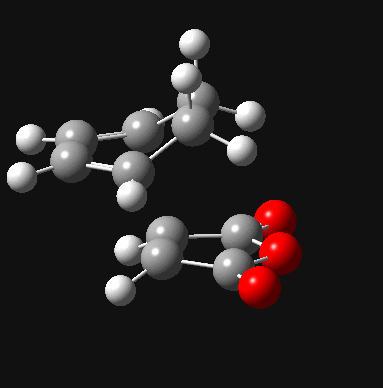- 812
Endo DOI:10042/to-8040			-806

Firstly, for each transition state there was only one negative frequency computed. This vibrational mode corresponds to the transition state during which two sigma bonds are formed and one π bond is broken as shown above. The transition state leading to the endo product was computed to be 0.68 kcal/mol lower in energy than that leading to the exo product, which is consistent with theory. The reason for the higher stability of the endo transition state can be most accurately depicted during analysis of the HOMO and LUMO of each transition state, which are shown below.

HOMO-LUMOs Transition state

	HOMO	LUMO
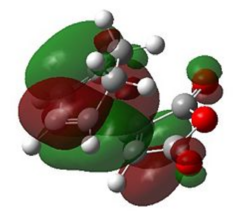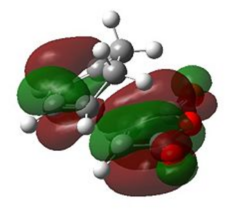Exo	HOMO	LUMO
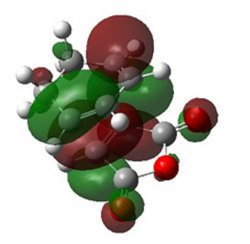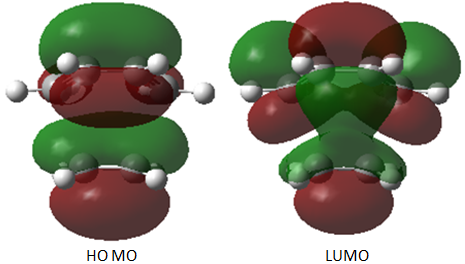
Endo	HOMO	LUMO

The natural bonding orbitals above indicate that in all cases, the LUMO of maleic anhydride (a) is the key interacting orbital involved in bond formation with the diene. This is consistent with this orbital lying very low in energy due to the resonance forms shown above resulting from resonance forms which place a δ- charge on the carbonyl oxygen atoms and a δ+ charge on the carbon atoms which form the new bonds with cyclohexa-1,3-diene.

Indication of resonance contributions which place a δ+ charge on the dienophile, lowering the energy of the LUMO and increasing its reactivity and the yield observed during this reaction.

The HOMO of the transition state for both cases is antisymmetric (a). For the HOMO of both the endo and exo transition states, the interacting molecular orbital on cyclohexadiene indicate that it is the HOMO of the diene which is involved in bonding. This is consistent with the observed HOMO-LUMO interaction during the transition state, as both interacting orbitals are antisymmetric and it is therefore possible to conclude that the reaction is allowed. The small energy gap between the LUMO of maleic anhydride and the HOMO of cyclohexadiene is one of the reasons for the fast rate of reaction observed in this experiment, as the π-π* energy gap is low.

The LUMO of both the endo and exo transition states has also been computed and is shown above. This indicates the large contribution from the LUMO of maleic anhydride but the orbitals on the cyclohexadiene component are very similar but not identical to the HOMO of cyclohexadiene (the orbital contribution from the other two carbon atoms of the diene is not present).

IRC Calculations

In order to confirm that the transition states above represent the lowest energy along the minimum energy pathway from a transition structure down to its local minimum on a potential energy surface, an Intrinisic Reaction Coordinate calculation was completed for each structure. Exo-DOI:10042/to-8043 Endo-DOI:10042/to-8044 The final structures of the endo and exo products are also included below.

Exo-

Exo-

As each transition state has converged to a minimum, corresponding to the energy of either the endo or exo final products, this confirms that the transition states above strongly resemble those experienced in reality.

Transition State Geometry Comparisons

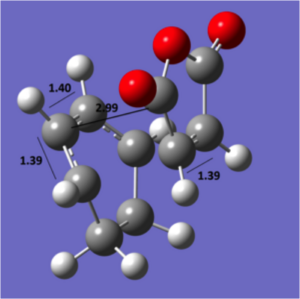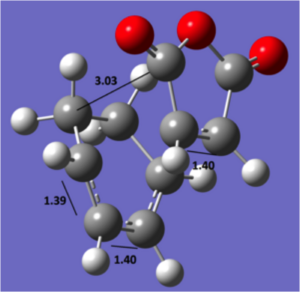
endo geometry	exo geometry

The diagram above shows the C-C bond lengths and the distance from the anhydride structure to the rest of the system. On initial analysis, the steric strain is expected to be less in the exo transition structure due to the slightly longer spacial distance of 3.03 Å between the anhydride and the opposite carbon atom. Additionally, the (to be) bridging carbons in the cyclohexadiene for the exo are sp³ hybridised and have 2 hydrogens, one of which is 2.75 Å away from the oxygen, compared to the planar hydrogen which points away at 3.45 Å for the endo form. However, if we were to follow the arguments presented previously, we would expect a stabilising Van der Waal attraction at the distance of 2.75 Å for the exo form. This suggests that there must be a different reason for the stability of the endo form. The molecular orbitals must therefore be considered.

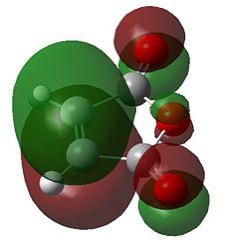
Secondary Orbital Effects

Extensive literature exists concerning the secondary orbital effect in the Diels-Alder reaction which accounts for the endo form being the kinetic product. In each case there is a balance between steric effects and secondary orbital overlaps (SOO). SOO has been defined as "the positive overlap of a non active frame in the frontier molecular orbitals of a pericyclic reaction", i.e. an interaction of orbitals not involved in the primary bond forming overlaps. Yet in some cases the presence of a bulky substituent can override this effect, as the endo approach becomes drastically sterically hindered.

Exo/Endo orbital effects

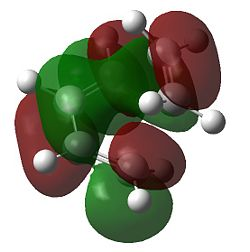
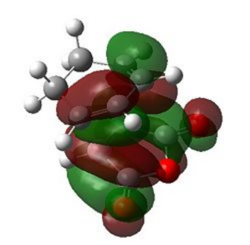
Approach	FMO approach	Calculated HOMO-1
Exo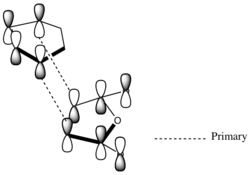
Endo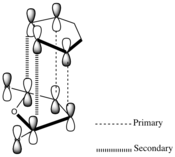

The interacting HOMO and LUMO drawn above indicate that additional bonding interactions (secondary orbital overlap) are present in the transition state leading to the endo product which do not exist in that leading to the exo product. Hence this results in the lower energy of the endo transition state computed above and results in this product dominating under kinetic conditions. The HOMO-1 of the transition state indicates the existence of the secondary orbital overlap in the endo transition state which are not present in that for the exo transition state. Although the secondary orbital overlap drawn above and that observed in the HOMO-1 do not agree completely, it emphasises the possibility of a numerous bonding interactions which may take place during the endo approach.

Additional Considerations

Solution Phase Organic Chemistry

Standard quantum chemical computations are performed on a single molecule or complex. This isolate species represents a molecule in the gas phase. Although gas-phase chemistry comprises an important chemical subdiscipline, the vast majority of reactions occur in solution. Hence if computational chemistry is to be relevant, most importantly for biochemical applications, treatment of the solvent is imperative.

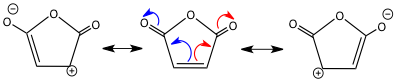
Neglecting solvent effects is extremely hazardous. Equilibria and kinetics can be dramatically altered by the nature of the solvent. For example, the rate of nucleophilic substitution reactions spans 20 orders of magnitude on going from the gas phase to nonpolar and polar solvents. A classic example of a dramatic solvent effect on equilibrium is the tautomerism between the compounds below. In the gas phase the equilibrium lies far to the left, but in solution, (b) dominates due to its much larger dipole moment.

Yet in the last ten years there have been a number of contributions to this area which has enabled a more accurate prediction of reaction outcomes to be made. For example, microsolvation computations, which involve computations with a few solvent molecules (typically no more than five), have provided a more in realistic insight into the nature of chemical reactions in solution. Implicit solvent models average out the effects of all of the solvent molecules, effectively integrating over the coordinates describing the solvent molecules.

The two methods described above have complementary strengths and weaknesses. The implicit solvation models treat the bulk, long-range effect of solvation, but may underestimate local effects within the first solvation shell, especially if hydrogen bonding can occur between the solute and solvent. Microsolvation addresses these local effects but may neglect long-range solvation effects. Hence it is likely that a combination of the two approaches might offer a treatment that combines the best of both methods.

Hybrid solvation models have been used to account for solvent effects, and seem to offer the most promising path for further explorations. This model surrounds the solute with a small number of explicit solvent molecules, and then embeds this cluster into the implicit dielectric field. A decision must be made regarding how many solvent molecules should be included in the cluster, recognizing that each additional solvent molecule increases the size of the calculation and expands the configuration space which must be included. Nonetheless, this model has been used successfully in a number of problems. For example, Cramer used this model to more accurately predict the free energy of dissociation for 57 species, mostly organic compounds, using the SM6 implicit solvation model. The results were improved by including a single explicit water molecule in the calculations.

Aqueous Diels-Alder Reactions

With its concerted reaction mechanism implying little change in charge distribution along the pathway, the Diels-Alder reaction has been understood to have little rate dependence on solvent choice. The relative rate for the Diels-Alder reaction of isopropene with maleic anhydride varies by only a factor of 13 with solvents whose dielectric constants vary by almost a factor of ten.

In this context, the surprise brought on by Breslow’s publication of a study of the Diels-Alder reaction in water is understandable. Breslow noted that the reaction of cyclopentadiene with acrylonitrile is twice as fast in methanol than in isooctane, but 30 times faster in water. An even larger acceleration was found for the reaction for the reaction of cyclopentadiene with butanone, shown below. The reaction is 741 times faster in water in water than in isooctane.

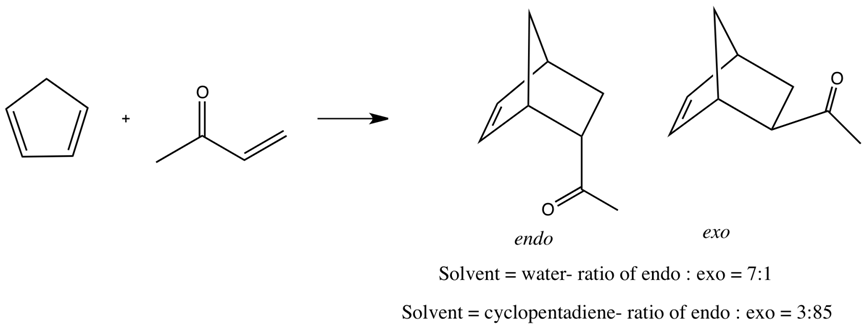
Water also produces an enhanced selectivity for the endo over the exo product; a greater than 20:1 ratio for the reaction above. Breslow attributed the enhanced rate for the Diels-Alder reaction in water to the hydrophobic effect. Engberts argued that in water, the exposed surface area of the transition state is reduced, thereby reducing unfavourable hydrocarbon-water interactions in the transition state, leading to rate enhancements. This has been called the enforced hydrophobic interaction.

Solvophobicity, a parameter which correlates well with hydrophobicity and lipopholicity, has been found to correlate well with Diels-Alder reaction rates in a number of solvents, including water.

The computational work of Jorgensen’s group was key to key to bringing critical insight into the nature of the aqueous Diels-Alder reaction. Monte Carlo simulations were used to simulate the reaction above. They first optimized the geometry of the four possible transition states (shown below) at HF/3-21G, followed by single point energy calculations.

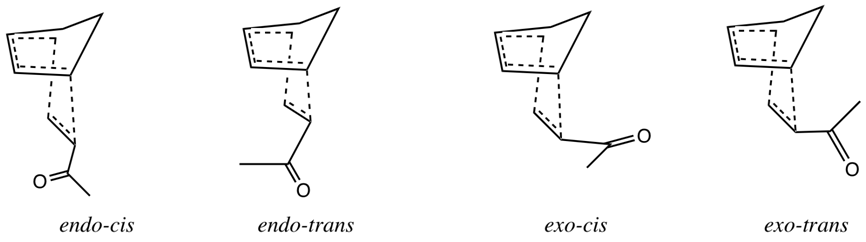
The lowest energy transition state was found to be endo cis conformation. A Monte Carlo simulation, including solvent molecules, was run, which indicated a 2.4 kcal/mol stabilization of the transition state in methanol, compared to completing the reaction in propane. The stabilization when water was used was predicted to be 4.2 kcal/mol, agreeing with the experimental value of 3.8 kcal/mol.

Their most important result concerns what effect could be responsible for the remaining stabilization (4.2 kcal/mol total less 1.5 kcal/mol due to the hydrophobic effect). Jorgensen noted that the number of hydrogen bonds to the carbonyl oxygen was fairly constant throughout the reaction (at an average of 2). However, each hydrogen bond was strongest in the neighborhood of the transition state. This is consistent with slightly more polar C-O bonds, as determined by the Mulliken charges, in the transition state than in the reactant or product. The degree of endo cis selectivity was found to increase as the water content of the solvent increased, suggesting that additional stabilization by this conformer in the transition state is could be present.

Endo/exo selectivity has also been predicted successfully using a variety of computational methods.

Conclusion

This investigation highlighted the attractiveness of computational methods to calculate and visualise transition states. In part one, the Cope rearrangement was studied, with the initial computations on 1,5-hexadiene conformers showing the energy differences between various anti and gauche structures. Molecular orbital analysis and measurement of the distance between various atoms to gauge strength of Van der Waals forces enabled each of the energy differences to be explained. A variety of methods were then used to compute the energies of the boat and chair transition structures, for example using frozen coordinates and the QST 2 method, which concluded that the boat transition structure was higher in energy than the chair transition state. The intrinsic reaction coordinate calculation confirmed that the transition states computed led to a minimum, and enabled the final structures to be compared.

Computations involving the Diels-Alder cycloaddition were then studied. Molecular orbital analysis enabled a clear explanation for why each reaction was symmetry allowed, as the HOMO-LUMO interactions could be visualised in Gaussian. The same techniques were used to study the regioselective reaction of cis-butadiene with maleic anhydride, and the secondary orbital overlap explained why the endo form is the kinetic product. Additional considerations were also explored, for example the effect of using water as the solvent in Diels-Alder reactions and also the introduction of solvent parameters to more accurately understand reactions in solution.

These computations emphasise the detailed insights into reactivity and selectivity which can be gained from relatively quick calculations, and similar calculations have also be used (as reported recently in Nature) to probe a variety of biologically relevant receptor-ligand binding interactions. Clearly the information gained from initial calculations are likely to save time in chemical synthesis as well, enabling potential synthetic pathways to be analysed before entering the laboratory.

Computational chemistry is rapidly emerging as a subfield of theoretical chemistry, where the primary focus is on solving chemically related problems by calculation. One of the main problems in this area is selecting a suitable level of theory for a given problem, and to be able to evaluate the quality of the obtained results. Yet this investigation has demonstrated the wealth of information which can be gained after a suitable method is chosen, emphasizing the increasing value of these computations as more systems are studied in the future.