Transition Structure and Reactivity

Felix de Courcy-Ireland 01062960 Transition States and Reactivity Computational Lab

Introduction

Stationary points on potential energy surfaces (or ‘hypersurfaces’) are defined by a value of zero for the first derivative at that point⁽¹⁾. However, it is through the use of second derivatives that the distinction can be made between the various types of stationary points, including reactants, transition states, intermediates and products⁽¹⁾.

Products, reactants and intermediates are all minima on a potential energy surface. They are characterised by the fact that all paths through these points have a positive second derivative⁽¹⁾.

Transition states are characterised by having a single normal coordinate for which the second derivative is negative, with all other paths through the transition state giving a positive second derivative at this point⁽¹⁾. They are known as ‘saddle-points’. If a point on a potential energy surface is a maximum in more than one normal coordinate, it is diagnostic that there is a lower energy path for the reaction to proceed in the vicinity of this point⁽¹⁾.

Nf710 (talk) 09:09, 23 March 2018 (UTC) This is a good explanation. But remember that you are working in 3N-6 coordinates.

The calculations carried out were effectively an interrogation of the potential energy surface of a simple reaction. The aims of the calculations were to locate the stationary points of the potential energy surfaces. This was done through using the Gaussian software, which traced paths across the potential energy surface, iteratively calculating the second derivative of each point on the path until a point with a zero first derivative was reached.

In this laboratory, a successfully located transition state was denoted by there being a single negative frequency in the frequency calculation, which when animated, showed the desired reaction coordinate for the reaction.

In the relatively simple reactions investigated, where the reactants pass through only one transition state, it is simple to calculate important quantities such as the activation energy and the reaction energy, from knowledge of the free energies of the reactants, products and transition states.

In this laboratory, two computational methods were used; the semi-empirical PM6 method and the DFT method B3LYP/6-31(d).

The semi-empirical PM6 is a less accurate method but not as computationally expensive. Therefore, it proved useful in optimising structures, be they reactants, products or transition states, in preparation for the use of the more accurate and expensive B3LYP method. B3LYP/6-31(d) is based in density functional theory (DFT)⁽¹⁾. DFT finds approximate solutions to unsolvable many-electron wave functions by analysis of functionals of the one electron density, ρ(r), of the molecule⁽¹⁾.

In some instances, use of chemical intuition in the location of transition states was most useful. There were cases where it proved fruitful to optimise a product or reactant(s) at the PM6 level, and then freeze the atoms immediately involved in the transition and further minimise the molecule around this frozen ‘transition state’ at the B3LYP level. A final calculation to find the transition state of at the B3LYP level was often more successful when using this ‘bond freezing’ technique.

Nf710 (talk) 09:09, 23 March 2018 (UTC) OK intro, you could have gone into more detail in part and added some equations/ diagrams

Exercise 1

(Fv611 (talk) Excellent work throughout the whole section - well done!)

Reaction Scheme

Log Files

Log Files - Butadiene + Ethene
Log Files - Butadiene + Ethene
Minimisation of butadiene (PM6)	Minimisation of butadiene (PM6)
Minimisation of ethene (PM6)	Minimisation of ethene (PM6)
Minimisation of cyclohexene (PM6)	Minimisation of cyclohexene (PM6)
Transition State (PM6)	Transition State (PM6)
IRC (PM6)	IRC (PM6)

MO diagram

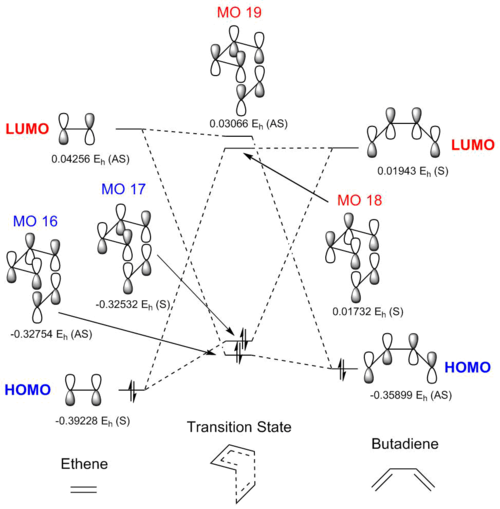
The above molecular orbital diagram shows the interaction between the HOMOs and LUMOs of the ethene and butadiene. Each MO is assigned a symmetry value (assignments were based on the phasing of orbitals) - from these assignments it can be seen that only orbitals of like symmetry interact. The orbital overlap integral is zero for the case of a symmetric-(anti-symmetric) interaction and non-zero for either a symmetric-symmetric or (anti-symmetric)-(anti-symmetric) interaction. The orbital energies are relative to one another rather than being absolute. An attempt has been made to draw the MOs of the transition state - the calculated MOs can be found in the table below.

Jmols of the HOMOs and LUMOS of Butadiene and Ethene

Table 1 showing the HOMO and LUMO of ethene with relative energies in Hartrees

Ethene

HOMO

Ethene HOMO

-0.39228 E_h

LUMO

Ethene LUMO

0.04256 E_h

Table 2 showing the HOMO and LUMO of butadiene, with relative energies in Hartrees.

Butadiene

HOMO

Butadiene HOMO

-0.35899 E_h

LUMO

Butadiene LUMO

0.01943 E_h

Jmols of the MOs in the Transition State

Table 3 showing the four MOs produced from the interaction of the ethene and butadiene MOs with associated relative energies in Hartrees

Transition State

MO 16

-0.32754 E_h

MO 17

-0.32532 E_h

MO 18

0.01732 E_h

MO 19

0.03066 E_h

C-C Bond Lengths of Reactants, Transition State and Products

Reaction Scheme repeated for clarity when analysing the bond lengths below.

Table 4 showing bond distances in the reactants.
Reactants
Bond	C-C Bond Distance (Å)
C1-C2	1.33344
C2-C3	1.47077
C3-C4	1.33344
C5-C6	1.32731

Table 5 showing bond distances in the transition state
Transition State
Bond	C-C Bond Distance (Å)
C1-C2	1.37978
C2-C3	1.41104
C3-C4	1.37981
C4-C5	2.11452
C5-C6	1.38177
C6-C1	2.11469

Table 6 showing bond distances in the product
Cyclohexene
Bond	C-C Bond Distance (Å)
C1-C2	1.49118
C2-C3	1.36309
C3-C4	1.49118
C4-C5	1.58345
C5-C6	1.56027
C6-C1	1.58345

Discussion of carbon-carbon (C-C) bond lengths

The C-C single bond length of typical n-hydrocarbon is 1.533 Å, and the bond length of a typical C-C double bond is 1.33 Å⁽²⁾. These lengths will be used as a point of comparison in the following discussion.

The two pairs of carbon atoms which make up the two alkene bonds in the butadiene (C1-C2 and C3-C4) lengthen from a separation of 1.33 Å to a separation of 1.49 Å. This can be rationalised by observing that these two double bonds in the butadiene reactant will be present in the cyclohexene product as single bonds in the cyclohexene ring.

The internal C-C bond in butadiene (C2-C3) shortens from a distance of 1.47 Å to a distance of 1.36 Å. Again, although this bond is shorter than a typical C-C single bond due to the conjugation of the butadiene, it shortens to a distance more typical of a C-C double bond which it adopts in the cyclohexene product.

The ethene C-C double bond lengthens from 1.327 Å to 1.560 Å. This is due to the carbons moving from the sp² hybridised environment of the ethene molecule to the sp³ hybridised environment of the cyclohexene ring.

The two new C-C bonds which are formed upon the Diels-Alder [4+2] cycloaddition between the butadiene and ethene have a value of 2.115 Å in the transition state, which shortens to a value of 1.583 Å in the cyclohexene product. This change in bond distance shows a shortening of bond lengths from an effectively infinite value in the reactants, through to a bond distance of 1.583 Å in the cyclohexene product.

Van der Waals radius of a carbon atom is 1.7 Å ⁽³⁾, and this can be used in discussion of the partially formed bond between the ethene and butadiene in the transition state.

The length of the partly formed C-C bonds between butadiene and ethene is 2.115 Å. This is less than two times the van der Waals radius of carbon. Therefore, although there is not formally a bond formed between the atoms, the atoms are close enough to interact through van der Waals forces.

Vibration corresponding to the transition state

Reaction Path Vibration

The Jmol above shows the vibration that corresponds to the reaction path at the transition state. It shows that the formation of the two bonds is synchronous - both bonds form simultaneously⁽⁴⁾.

Exercise 2

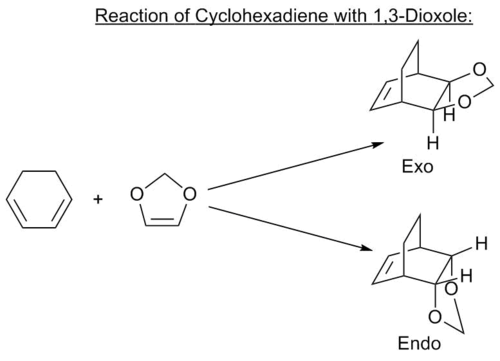
Reaction Scheme

Log files

Log Files - 1,3-Dioxole + Cyclohexadiene
Log Files - 1,3-Dioxole + Cyclohexadiene
Minimised Cyclohexadiene (B3LYP/6-31G(d))	Minimised Cyclohexadiene (B3LYP/6-31G(d))
Minimised 1,3-Dioxole (B3LYP/6-31G(d))	Minimised 1,3-Dioxole (B3LYP/6-31G(d))
Minimised exo-product (B3LYP/6-31G(d))	Minimised exo-product (B3LYP/6-31G(d))
Minimised endo-product (B3LYP/6-31G(d))	Minimised endo-product (B3LYP/6-31G(d))
Minimised exo-transition state (B3LYP/6-31G(d))	Minimised exo-transition state (B3LYP/6-31G(d))
Minimised endo-transition state (B3LYP/6-31G(d))	Minimised endo-transition state (B3LYP/6-31G(d))
IRC on Exo Transition State (PM6)	IRC on Exo Transition State (PM6)
IRC on Endo Transition State (PM6)	IRC on Endo Transition State (PM6)
Single Point Energy on Exo Transition State (B3LYP/6-31G(d))	Single Point Energy on Exo Transition State (B3LYP/6-31G(d))
Single Point Energy on Endo Transition State (B3LYP/6-31G(d))	Single Point Energy on Endo Transition State (B3LYP/6-31G(d))

(Fv611 (talk) Very nice MO diagrams here too. )

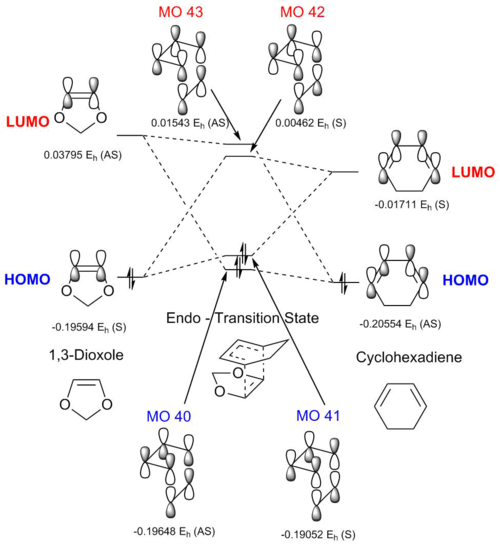
Jmols and Molecular Orbital Diagram for the Endo Reaction of Cyclohexadiene and 1,3-Dioxole

Table 7 showing the MOs of the endo transition state with associated relative energies in Hartrees

Transition State

MO 40 - Endo Transition State

-0.19648 E_h

MO 41 - Endo Transition State

-0.19052 E_h

MO 42 - Endo Transition State

0.00462 E_h

MO 43 - Endo Transition State

0.01543 E_h

Above is the new MO diagram from the endo reaction of cyclohexadiene and 1,3-dioxole. The endo reaction involves the two oxygen atoms of the 1,3-dioxole tucking under the cyclohexadiene. This leads to a stabilising secondary orbital interaction which shall be discussed later. The MO's produced by the interaction of the cyclohexadiene and 1,3-dioxole orbitals are shown in Table 7.

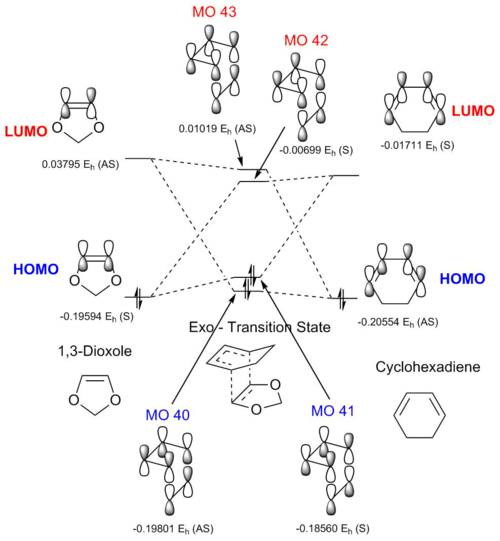
Jmols and Molecular Orbital Diagram for the Exo Reaction of Cyclohexadiene and 1,3-Dioxole

Table 8 showing the MOs of the exo transition state with associated relative energies in Hartrees

Transition State

MO 40 - Exo Transition State

-0.19801 E_h

MO 41 - Exo Transition State

-0.18560 E_h

MO 42 - Exo Transition State

-0.00699 E_h

MO 43 - Exo Transition State

0.01019 E_h

Above is the MO diagram from the exo transition state, with the MOs produced from interaction of the reactant HOMOs and LUMOs shown in Table 8. It should be noted that, similarly to the previous Diels-Alder reaction of butadiene and ethene, that only orbitals of like symmetry interact to give MOs in the transition state.

Inverse and Normal Electron Demand Diels-Alder Reactions

The reaction between 1,3-dioxole and cyclohexadiene is an inverse electron demand Diels-Alder reaction. Inverse electron demand Diels-Alder reactions are characterised by there being a smaller energy gap between the HOMO of the dienophile (1,3-dioxole) and the LUMO of the diene (cyclohexadiene) than the energy gap between the HOMO of the diene and the LUMO of the dienophile⁽⁵⁾.

Nf710 (talk) 09:12, 23 March 2018 (UTC) This is correct however you have just stated it with no values. You have even done a single point energy calculation too! Why not use the numbers for the MOs that you have calculated to prove your hypothesis.

Thermochemistry

If the formation of more than one product is possible from a given set of reactants, knowledge of reaction energies and activation energies can lead to assignment of the kinetic and thermodynamic products. The kinetically favourable product is that from the reaction which has the lowest energy barrier to conversion between reactants and products. The thermodynamically favourable product is the lower energy product relative to the reactant(s).

In the case that there are two possible products of a reaction, as is the situation in this Diels-Alder reaction between 1,3-dioxole and cyclohexadiene, it is not necessary for one product to be the thermodynamic product and the other product to be the kinetic product. It may be the case that one of the products is both the thermodynamic and kinetic product.

Energies Endo Reaction
Molecule	Gibbs Free Energy (kJ/mol)
1,3dioxole	-701,188.414
cyclohexadiene	-612,592.877
1,3dioxole and cyclohexadiene	-1,313,781.291
Endo Transition State	-1,313,621.479
Endo Product	-1,313,848.695

Endo Reaction Parameters
Reaction Barrier (kJ/mol)	159.811
Reaction Energy (kJ/mol)	-67.404

Energies Exo Reaction
Molecule	Gibbs Free Energy (kJ/mol)
1,3dioxole	-701,188.414
cyclohexadiene	-612,592.877
1,3dioxole and cyclohexadiene	-1,313,781.291
Exo Transition State	-1,313,613.639
Exo Product	-1,313,845.098

Exo Reaction Parameters
Reaction Barrier (kJ/mol)	167.651
Reaction Energy (kJ/mol)	-63.807

As shown in the above tables, the reaction barrier for the exo reaction is higher at a value of 167.651 kJ/mol, due to the transition state through which the reaction proceeds being of higher energy. Therefore, due to the lower reaction barrier of 159.811 kJ/mol, the endo product is kinetic product.

The endo product proceeds through a lower energy transition state due to the secondary orbital interactions between the oxygen p orbitals and the p orbitals of the internal carbons of the cis-butadiene fragment⁽⁵⁾.

The Jmol of the HOMO of the endo transition state is repeated here, where it can be seen that there is a stabilising interaction between the orbitals which lie on the oxygens of 1,3-dioxole and the two carbons which eventually form the double bond in the product, for the portion of the orbital located in these areas is the same phase.

MO 41 - Endo Transition State

The endo product is again the thermodynamic product, as the energy of the endo product (-67.404 kJ/mol) is lower than that of the exo product (-63.807) - although the difference in energy is less in the products than in the reactants. This reason for the greater stabilisation of the endo product is possibly due to this same orbital interaction between the p orbitals on the oxygens with the alkene pi system. The fact that the difference in energy between the products is less than the difference in energy of the transition states is a consequence of this orbital interaction being poorer in the products.

Nf710 (talk) 09:14, 23 March 2018 (UTC) This is a good section. You have got the correct energies and come to the correct conclusions. However there are part where you could have gone into more detail. Such as the thermo and kinetic theory, or the electron demand.

Exercise 3

Log Files

Reaction of Sulfur Dioxide with Exo-Cyclic Cis-Butadiene Fragment

Log Files - Dioxide + Exo-Cyclic Butadiene
Reaction of Sulfur Dioxide with Exo-Cyclic Cis-Butadiene Fragment
Xylylene Minimisation (PM6)	File:XYLYLENE MINIMISATION PM6.LOG
Sulfur Dioxide Minimisation (PM6)	File:SULFUR DIOXIDE.LOG
Cheletropic Transition State (PM6)]	File:CHELETROPIC PM6 PRODUCT TRANSITIONSTATE NOTFROZEN.LOG
Cheletropic Product (PM6)]	File:CHELETROPIC PRODUCT INITIAL MINIMISATION 2.LOG
Endo (Xylylene-SO2) Transition State (PM6)	File:DA ENDO PM6 TRANSITIONSTATE ATTEMPT1.LOG
Endo (Xylylene-SO2) Product (PM6)]	File:DA ENDO PM6 PRODUCT ATTEMPT1 NOTFROZEN MINIMISATION.LOG
Exo (Xylylene-SO2) Transition State (PM6)]	File:DA EXO PM6 TRANSITIONSTATE SECOND.LOG
Cheletropic IRC (PM6)]	File:CHELETROPIC PM6 IRC ATTEMPT1.LOG
Endo (Xylylene-SO2) IRC (PM6)	File:DA ENDO PM6 IRC ATTEMPT1.LOG
Exo (Xylylene-SO2) IRC (PM6)]	File:DA EXO PM6 IRC ATTEMPT1.LOG

Reaction of Sulfur with Alternate, Endo-Cyclic Cis-Butadiene Fragment of Xylylene

Log Files - Dioxide + Endo-Cyclic Butadiene
Reaction of Sulfur Dioxide with Exo-Cyclic Cis-Butadiene Fragment
Endo Transition State - OTHER CIS-BUTADIENE FRAGMENT OF XYLYLENE]	File:ENDO EXTRA NEW TRANSITIONSTATE ATTEMPT2.LOG
Endo Product Minimisation - OTHER CIS-BUTADIENE FRAGMENT OF XYLYLENE	File:ENDO EXTRA NEW MINIMISATION ATTEMPT1.LOG
Exo Transition State - OTHER CIS-BUTADIENE FRAGMENT OF XYLYLENE	File:EXO EXTRA TRANSITIONSTATE ATTEMPT1.LOG
Exo Product Minimisation - OTHER CIS-BUTADIENE FRAGMENT OF XYLYLENE	File:EXO EXTRA MINIMISATION ATTEMPT1.LOG
Cheletropic Transition State - OTHER CIS-BUTADIENE FRAGMENT OF XYLYLENE	File:CHELETROPIC EXTRA TRANSITIONSTATE NOTFROZEN ATTEMPT2.LOG
Cheletropic Product Minimisation - OTHER CIS-BUTADIENE FRAGMENT OF XYLYLENE	File:CHELETROPIC PRODUC MINIMISATION HOPEFULLY ATTEMPT2.LOG

GIFs of IRC for Reaction of Sulfur Dioxide and Xylylene

It can be seen in all of the GIFs of the reactions below that the 6-membered ring of the highly unstable xylylene molecule becomes aromatic on reaction with sulfur dioxide.

GIF for Endo Reaction

GIF for Exo Reaction

This reaction goes from products to reactants.

GIF for Cheletropic Reaction

Thermochemistry

Reaction Parameters For Reaction of Sulfur Dioxide With Xylylene
Reaction Type	Reaction Barrier (kJ/mol)	Reaction Energy (kJ/mol)
Endo	81.724	-99.050
Exo	85.709	-99.714
Cheletropic	104.049	-156.041

The data above shows that the kinetic product is the endo product, due to it having the lowest reaction barrier of 111.946 kJ/mol. This is probably a consequence of the secondary orbitals interactions that were previously discussed, between the second sulfur oxygen and the carbon p orbitals that eventually form the alkene. The cheletropic reaction has the highest reaction barrier of 140.666 kJ/mol. This is potentially due to the 5-membered transition states that forms being of higher energy than that of the 6-membered transition states that form in the endo and exo forms of the reaction.

(The barriers in this text refer to the alternate reactions Tam10 (talk) 15:32, 16 March 2018 (UTC))

The thermodynamic product is also that from the endo reaction, due to it having the lowest energy (-156.041 kJ/mol). This is best explained in terms of bond enthalpies. In the endo and exo reactions, a sulfur-oxygen bond is broken and a carbon-oxygen and sulfur-carbon bond are formed, whereas in the cheletropic reaction, no bonds are broken, and two bonds are formed.

Although the cheletropic reaction proceeds through a higher energy transition states, the formation of two bonds with the loss of none leads to a lower energy product.

Reaction Profile for the Reaction of Sulfur Dioxide and the Exo-Cyclic Cis-Butadiene Fragment of Xylylene

Further Comment

Discussion of Stability of Xylylene

Xylylene is an 8 electron system, and therefore anti-aromatic (Huckel's 4n rule, with n=2)⁽⁵⁾. These systems are often bent to avoid planarity of the p orbitals of the molecule, however xylylene is somewhat constrained to a planar configuration due to the sp²) nature of the 6 ring carbons. This makes for a very strained molecule with a high relative energy of 467.460 kJ/mol.

Reaction at the Endo-Cyclic, Cis-Butadiene Fragment

Reaction scheme above shows the same reactions are possible at the endo-cyclic cis-butadiene fragment of xylylene.

Reaction Parameters For Reaction at the Alternate Cis-Butadiene Site of Xylylene
Reaction Type	Reaction Barrier (kJ/mol)	Reaction Energy (kJ/mol)
Endo	111.946	16.197
Exo	119.783	20.668
Cheletropic	140.666	47.238

The values for activation energy (reaction barrier) and reaction energy above show these reactions are far less favoured. All the reactions are endothermic, and also have larger reactions barriers than the reactions at the original cis-butadiene fragment.

The reason for the positive values for the reaction energy is due to the fact that there is no gain of aromaticity in these reactions, like there was previously.

The reason for the higher activation barrier is potentially a consequence of the endo-cyclic cis-butadiene fragment being harder to access, therefore the molecules need to adopt higher energy conformations in the transition states to yield the products

Further Work

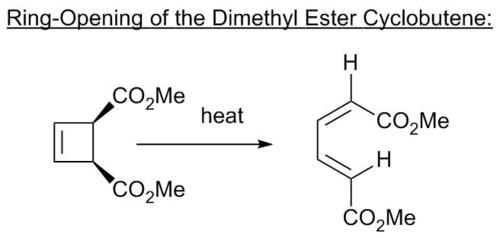
Ring Opening of the Dimethyl Ester Cyclobutene

Log Files

Ring Opening of the Dimethyl Ester Cyclobutene
Ring Opening of the Dimethyl Ester Cyclobutene
Dimethyl Ester of Cyclobutene	Dimethyl Ester of Cyclobutene
Transition State	Transition State
Diene Product	Diene Product
IRC Calculation	IRC Calculations

Jmols of MOs

Jmols of MOs for Ring Opening of the Dimethyl Ester Cyclobutene

HOMO

LUMO

Reactant (ring closed)

Reactant HOMO

Reactant LUMO

Transition State

Transition State HOMO

Transition State LUMO

Product (ring open)

Product HOMO

Product LUMO

Disrotatory or Conrotatory?

Due to running out of time, I have not been able to put the correct MO for the transition state into the table above (I am doing something wrong, but I am sure that the marker will be able to work out what it is I have done). However, the reaction proceeds in a conrotatory fashion, as expected due to it being a 4n cyclisation under thermal conditions⁽⁵⁾.

(So what's happened is that you're showing the MOs of the initial geometries of the calculations eg product frame should be 64 not 2. Yes this reaction is conrotatory as you're on the ground state Tam10 (talk) 15:41, 16 March 2018 (UTC))

Cyclisation of [1,1']bicyclohexyl-1,1'-diene

Log Files

Cyclisation of [1,1']bicyclohexyl-1,1'-diene
Cyclisation of [1,1']bicyclohexyl-1,1'-diene
[1,1']bicyclohexyl-1,1'-diene	[1,1']bicyclohexyl-1,1'-diene
Transition State	Transition State
Cyclised Product	Cyclised Product
IRC Calculation	IRC Calculation

Jmols of MOs

Jmols of MOs for Cyclisation of [1,1']bicyclohexyl-1,1'-diene

HOMO

LUMO

Reactant (ring open)

Reactant HOMO

Reactant LUMO

Transition State

Transition State HOMO

Transition State LUMO

Product (ring closed)

Product HOMO

Product LUMO

(The same problem as before, but perhaps worse here. You've started with geometries that have a plane of symmetry, which in this case have favoured MOs with the same symmetry (just happen to correspond to the orbitals that would be populated under photochemical conditions). If you use the correct frame you'll see that it is all conrotation. Also observing the IRC should show the same result. Perhaps important to know is PM6 is a ground state, single-reference method Tam10 (talk) 15:41, 16 March 2018 (UTC))

Disrotatory or Conrotatory?

As can be seen from the MOs of the transition state structures for the cyclisation of this [1,1']bicyclohexyl-1,1'-diene, the cyclisation proceeds in a disrotatory fashion, with either end of the butadiene fragment twisting in the opposite direction. This is anticipated due to it being a 4n cyclisation performed under photochemical conditions⁽⁵⁾.

Conclusion

A computational analysis of three different reactions of increasingly complexity were studied. Through the introduction to Gaussian, two computational methods were used (PM6 and B3LYP/6-31(d)) to optimise both the reactants and products of a reaction. From these initial minimisations, and using chemical intuition, the transition states for these reactions were located.

From using the relative energies of the transition states, reactants and products, thermodynamic properties of the systems were calculated (the activation energy (reaction barrier) and reaction energy). These values were used in discussion of the thermodynamic and kinetic products of the reaction.

Further work was carried out on two electrocyclic reactions, however the student ran out of time to conduct a full analysis of these reactions, for said was enjoying carrying out the calculations too much.

The tutorial and further reading provided facilitated an introduction to potential energy surfaces and the underlying quantum mechanics of the Gaussian code. A computational chemist must marry a working knowledge of the computational methods (and underlying approximations) with the savoir-faire of an experimental chemist.

References

Template loop detected: Template:Reflist

1. W. J. Ot, Computational quantum chemistry, 1990, vol. 207.

2. L. S. Bartell, J. Am. Chem. Soc., 1959, 81, 3497–3498.

3. A. Bondi, J. Phys. Chem., 1964, 68, 441–451.

4. B. R. Beno, K. N. Houk and D. A. Singleton, J. Am. Chem. Soc., 1996, 118, 9984–9985.

5. J.Clayden, Organic Chemistry, OUP, Oxford, 2001

6. E. Białkowska-Jaworska, M. Jaworski and Z. Kisiel, J. Mol. Struct., 1995, 350, 247–254.