Jump to content

Rep:Error9999

From ChemWiki

Introduction

The experiment mainly focuses on locating and characterising transition states, including optimization,frequency calculation and IRC of those for 3 Diels-Alder reactions.

In the context of a potential energy surface, a minimum is the lowest energy point, which can be either reactant or product. A transition state is a saddle point with a single negative Hessian eigenvalue,ω21. They both have zero gradient, i.e. zero first derivative and negative secondary derivative.

The experiment allows us to explore the transition state of Diels-Alder reactions with optimization and various confirmations.

Nf710 (talk) 11:55, 16 November 2017 (UTC) This is extremely brief and it would have been good if you could have talk about the methods in some detail.

Exercise 1: Reaction of Butadiene with Ethylene

Calculation

Analysis

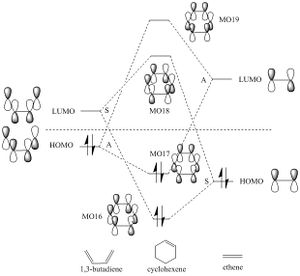
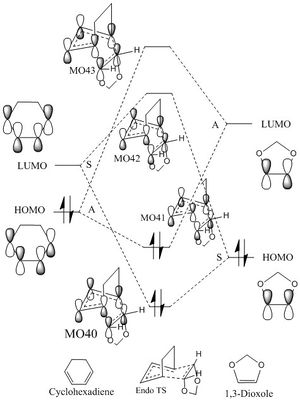
  • The MO diagram of ethene and butadiene DA reaction is drawn below:
For an 'allowed' reaction, a symmetric MO must interact with a symmetric MO, and an anti-symmetric one must interact with an anti-symmetric one. Symmetric anti-symmetric with anti-symmetric or vice versa are 'forbidden' reactions.

(Fv611 (talk) Proofreading would help - I know what you want to write here but this sentence doesn't make sense)

In this case, the anti-symmetric HOMO of butadiene and the anti-symmetric LUMO of ethene interact together; the symmetric LUMO of butadiene and the symmetric HOMO of ethene interact, both of which react suprafacially and conserve symmetry.

The orbital overlap integral is zero for the case of a symmetric-antisymmetric interaction, and non-zero for a symmetric-symmetric interaction and an antisymmetric-antisymmetric interaction.

(Fv611 (talk) Could have linked the symmetry requirements to the orbital overlap)

(Fv611 (talk) Your MO diagram is wrong. You react symmetric reactant MOs to give antisymmetric orbitals, and viceversa. Something must have gone wrong in the MO calculation as MO16 should be antisymmetric and MO17 should be symmetric. I think it is because you didn't optimise that transition state and instead just ran a freq calculation with the MO keyword. However, MO18 and MO19 are correct in the table but you do not correlate them with your MO diagram, where they are drawn with opposite symmetries.)

  • The MOs for HOMOs, LUMOs and combined orbitals of ethene and butadiene are shown below:
HOMO for Butadiene LUMO for Butadiene HOMO for Ethylene LUMO for Ethylene
Interact with LUMO of ethene Interact with HOMO of ethene Interact with LUMO of butadiene Interact with HOMO of butadiene
MO 16 for TS MO 17 for TS MO 18 for TS MO 19 for TS
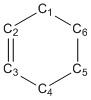
  • The bond lengths change during the Diels-Alder reaction as hybridisation changes:
Reactants Transition State Product Comments
Typical sp3 and sp2 C-C bond lengths are 1.54Å and 1.47Å. The Van der Waals radius of the C atom is 1.70Å. The partly formed C-C bonds in the TS are much longer than sp3 and sp2 C-C bond lengths but are shorter than the Van der Waals radius.

(Fv611 (talk) Are they? Because you state that the VdW radius is 1.7 and the TS bond length is 2.11.)

bond number bond length bond number bond length bond number bond length bond lengths change as the reaction progresses
C1=C2,C3=C4 1.335Å C1...C2,C3...C4 1.380Å C1-C2,C3-C4 1.500Å C1=C2 and C3=C4 are weakened and lengthened.
C2-C3 1.468Å C2...C3 1.411Å C2=C3 1.337Å C2-C3 is strengthened and shortened.
C5=C6 1.327Å C5...C6 1.382Å C4-C5,C5-C6,C6-C1 1.537Å C5=C6 is weakened and lengthened.
C1...C6,C4...C5 2.115Å C1 and C6,C4 and C5 are approaching each other, forming a single bond.

The vibration that corresponds to the reaction path at the transition state is illustrated below. The formation of the two bonds are synchronous.(The gif will move if you click on it.)

Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

Calculation

Analysis

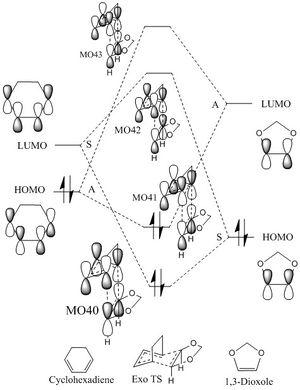
  • The MOs(HOMOs, LUMOs and combined orbitals) of endo- and exo- TSs at the B3LYP/6-31G(d) level are extracted as following:
Exo-TS MOs
MO43
MO41
MO42
MO40
Endo-TS MOs
MO43
MO41
MO42
MO40

(Your MOs don't correspond to the diagram you've produced. You are also linking MOs of the wrong symmetry Tam10 (talk) 16:43, 1 December 2017 (UTC))

  • Is it a normal or inverse demand DA reaction?

This is an inverse demand DA reaction. The energy for HOMO of cyclohexadiene is -0.32410 a.u. and that of LUMO of 1,3-dioxole is 0.02395 a.u. The energy difference is 0.34805a.u. The energy for LUMO of cyclohexadiene is 0.02134 a.u. and that for HOMO of 1,3-dioxole is -0.32462 a.u. The energy difference is 0.34596 a.u. Therefore, LUMOcyclohexadiene and HOMO1,3-dioxole energy difference is smaller than that of HOMOcyclohexadiene and LUMO1,3-dioxole. Thus, the LUMOcyclohexadiene and HOMO1,3-dioxole are the frontier orbitals that interact the most strongly, and result in the most energetically favourable bond formation.

  • Energies extracted and tabulated from .log files
1,3-dioxole cyclohexadiene exo product endo product exo TS endo TS
Ɛ0 + Gcorr -0.052279 0.116878 0.037973 0.037802 0.138907 0.137941
in kJ/mol -137.26 306.86 99.70 99.25 364.70 362.16
reaction barriers(kJ/mol) - - - - 195.10 192.56
reaction energies(kJ/mol) - - -69.90 -70.35 - -
notes The endo product is both kinetically and thermodynamically more favorable one.
  • Compare the HOMO of endo TS and that of exo TS

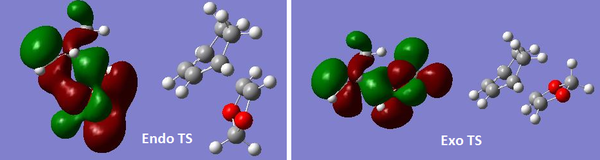
The left hand side image shows the MO for the HOMO of endo TS and its molecular structure. It is easily seen that despite the interaction between the alkene in the 1,3-dioxole and the diene in the cyclohexadiene, the MOs of oxygens in 1,3-dioxole and diene in the cyclohexadiene also interact. And this is the secondary orbital interactions of the endo TS, which lowers the energy and make it more kinetically favorable.However, the exo TS has only primary orbital interactions, and no other MOs interact apart from the alkene in the 1,3-dioxole and diene in cyclohexadiene.

Nf710 (talk) 12:10, 16 November 2017 (UTC) These calculation should have been done at B3LYP but you have still come to the correct conclusion. Good understanding of the secondary orbital interaction.

Exercise 3: Diels-Alder vs Cheletropic

Calculation

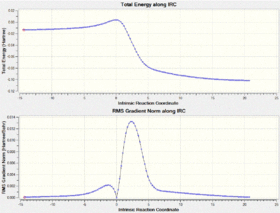
  • The TSs for the endo- and exo- Diels-Alder and the Cheletropic reactions are optimized at the PM6 level, and their IRCs are calculated to confirm them.
exo- Diels-Alder at PM6 level endo- Diels-Alder at PM6 level Cheletropic reactions at PM6 level
Media:XYLYLENEDA1-1-PM6(em2015).LOG Media:XYLYLENEDAENDO1-1-1-PM6(em2015).LOG Media:XYLYLENECHE1-1-1-1(em2015).LOG

Analysis

  • The energies from the .log files of each compound are tabulated and are sorted out in the following table:
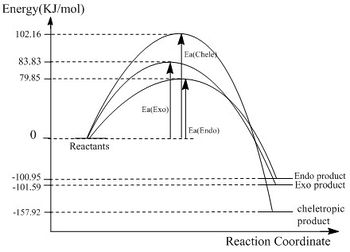
Xylylene SO2 DA exo product DA endo product cheletropic product exo ts endo ts cheletropic ts
Ɛ0 + Gcorr 0.178764 -0.118614 0.021454 0.021698 -0.000001 0.092077 0.090561 0.099061
in kJ/mol 469.34 -311.42 56.33 56.97 -0.003 241.75 237.77 260.08
reaction barriers(kJ/mol) - - - - - 83.83 79.85 102.16
reaction energies(kJ/mol) - - -101.59 -100.95 -157.92 - - -
notes The endo product is kinetically more favorable, and the cheletropic reaction is thermodynamically more stable.
  • The energies of reactants, reaction barriers and reaction energies are used to draw an energy profile, containing all three reactions.
In the reaction profile, the energy level of the reactants is set as zero. All three reactions are exothermic. The cheletropic reaction has the highest energy barrier and therefore needs the most activation energy. The reaction barriers and product energy levels are quite close for both Diels-Alder exo- and endo- reactions. However, endo- reaction has a transition state slightly lower in energy and a slightly higher product energy level. During the course of the reaction, two double bonds becomes three double bonds. The 6-membered ring is gaining aromaticity and forming benzene, which makes is stronger and more stabilized.

(Don't use curved lines like this for reaction profiles - they can be misleading. Also be more specific about which double bonds you are referring to. Could be useful to have a diagram for it Tam10 (talk) 14:06, 10 November 2017 (UTC))

Conclusion

The highest optimization of the TSs in this experiment is B3LYP and this method works very well, giving highly precise data and structures of the reactants, products and transition states.

Frequency calculations and IRCs are very good ways to confirm structures. For frequency calculations, the vibration of a molecule is essential and the lowest energy vibration is the motion of reaction. All three experiments uses it and results turn good. Regarding the IRC calculation, if sits right at the transition state, smooth reaction profile and zero-gradient of the barrier will be presented.

The first exercise gives the easiest and the most general form of a Diels-Alder reaction. From the reaction, general rules like orbital symmetry can be identified and proved. It also explores the change in bond length,e.g from double bond to single bond, the bond length increases and the bond is weakened. The bond lengths of transition state is somewhere in between the reactants and product.

Exercise 2 is an inverse demand DA due to the electron-withdrawing oxygens on the 1,3-dioxole. The energy gap between LUMOcyclohexadiene and HOMO1,3-dioxole is closer than the other pair. This part also explores the energy of the reaction and turns out that the endo product is both kinetically and thermodynamically more favorable. The seconday orbital interaction in the endo TS lowers the reaction energy barrier and make it more kinetically favorable than the exo product.

The last experiment compares three different reactions with the same reactants. And the result shows the endo product is kinetically more favorable, and the cheletropic reaction is thermodynamically more stable. The difference can be easily seen from the energy profile.

Locating TS is important and requires high level of optimisation. The whole experiment assists the modelling and finding the reaction paths on the energy surface.

Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Error9999&oldid=814943"