Rep:Egn14

Introduction

Potential Energy Surfaces (PES)

A Gaussian calculation involves the utilisation of the Born-Oppenheimer approximation to obtain energy values for every structure generated by varying 3N-6 degrees of freedom. A potential energy surface is obtained when two degrees of freedom are varied. By varying greater than two degrees of freedom we obtain a varying higher dimensional vector space with respect to energy.

Minimum points: A minimum is a turning point within the PES that corresponds to the minimum energy structural configuration. This has zero gradient and positive curvature (second derivative) as a minimum point can only increase by definition. A structure that is generated in the Gaussview builder represents an arbitrary point within the PES. When a Gaussian optimisation is performed, the program rolls down the PES along the path of steepest slope from this initial arbitrary energy point until it reaches the aforementioned minimum energy point. The minimum energy structure is hence generated. A frequency calculation is when Gaussian computes the second derivatives (curvature) corresponding to the vibrational modes. Therefore, a frequency calculation of a bona fide minimum would turn out only positive second derivatives and thus confirming a minimum.

Transition State: The transition state is a saddle point with a gradient of zero and corresponds to a local but not global maximum. More specifically, the transition state is a maximum along one direction (the reaction coordinate) and is a minimum along other directions. Mathematically, this means that a transition state has a negative curvature along the reaction coordinate (it is getting ready to roll down this pathway) and a positive curvature along all other directions. This is not unlike the shape of a saddle. A frequency calculation by Gaussian for a transition state would therefore produce multiple positive second derivatives (curvatures) along non-reactive coordinate paths and one negative second derivative along the reaction coordinate.

Nf710 (talk) 23:41, 15 December 2016 (UTC) Well explained conceptually, some equations would have been nice here.

Exercise 1: Reaction of Butadiene with Ethylene

Molecular Orbitals

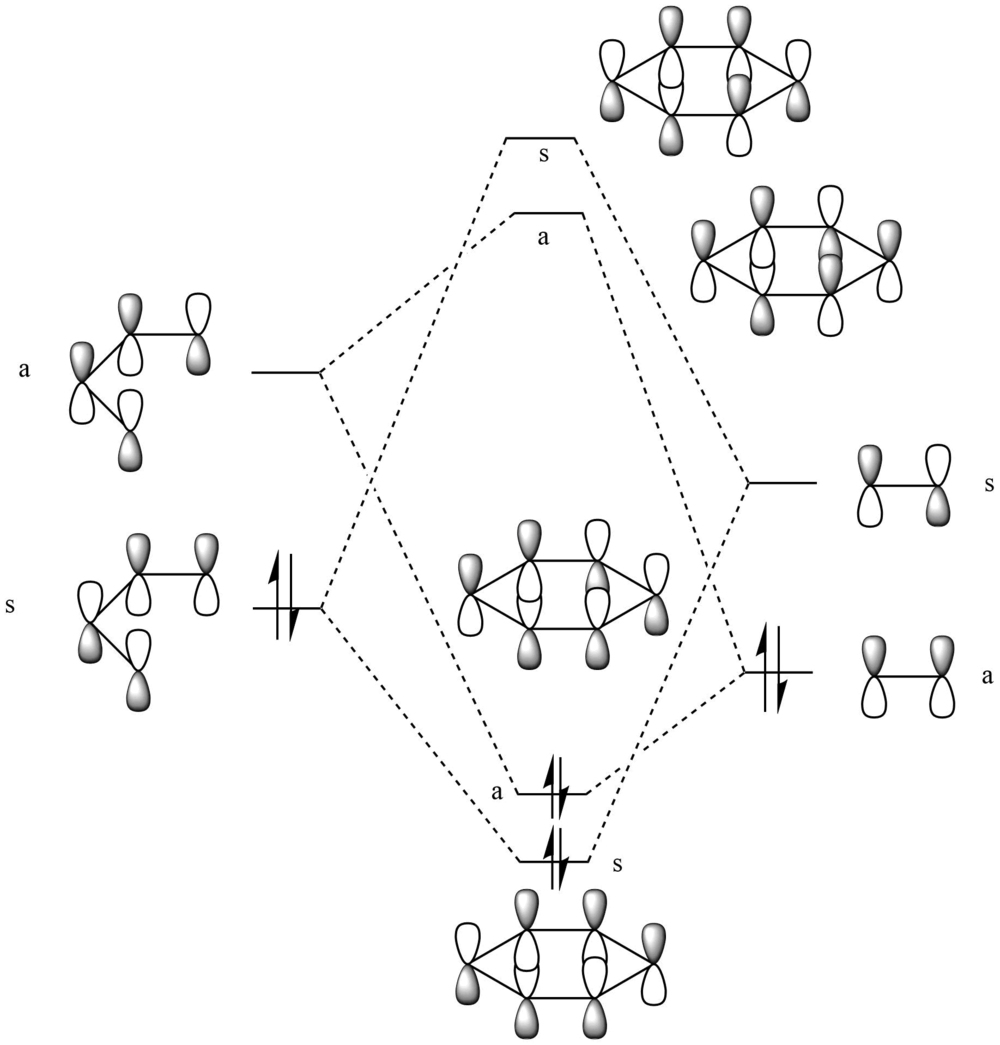
MO Diagram for Butadiene and Ethene Cycloaddition

Reactant/TS	Molecular Orbital	Symmetry	MO Surface
Ethene	HOMO	unsymmetric
Ethene	LUMO	symmetric
Butadiene	HOMO	symmetric
Butadiene	LUMO	unsymmetric
TS	2nd HOMO	symmetric
TS	HOMO	unsymmetric
TS	LUMO	unsymmetric
TS	2nd LUMO	symmetric
Table 1.

The HOMO of ethene interacts strongly with the LUMO of butadiene to form the the HOMO and LUMO of the TS. The LUMO of ethene and HOMO of butadiene interacts to give the 2nd HOMO and 2nd LUMO of the TS. An allowed reaction is one where the symmetries of interacting orbitals between reactants are the same. For example, the unsymmetric-unsymmetric interaction between the HOMO of ethene and LUMO of butadiene gives rise to the HOMO and LUMO of the TS in an allowed reaction. The orbital overlap integral is non-zero for same symmetry interactions, i.e symmetric-symmetric and antisymmetric-antisymmetric while the overlap integral is zero for opposite symmetry interactions, i.e symmetric-antisymmetric. This can be seen in the strong interactions between orbitals of the same symmetry in the above reaction. However the orbital overlap integral between the same symmetry orbitals from above is not one. An overlap integral with a value of one would only occur when overlap involves identical orbitals due to the orthonormality of basis sets.

Bond Lengths

	Ethene	Butadiene	Transition State	Product
Compound
Bond length (Å)	(C1=C2) = 1.328	(C1=C2) = (C3=C4) = 1.335 (C2=C3) = 1.468	(C1=C2) = (C3=C4) = 1.380 (C2=C3) = 1.411 (C4=C5) = 1.382 (C1-C5) = (C4-C6) = 2.115	(C1-C2) = (C5-C6) = 1.500 (C2-C3) = (C4-C5) = 1.540 (C3-C4) = 1.541 (C1-C6) = 1.338
Table 2.

1. The C=C double bonds in ethene and butadiene elongates going from reactants to transition state. All three C=C bonds then become C-C single bonds in the product.
2. The C-C single bond in butadiene shortens going from reactant stage to transition state. This bond then becomes a C=C double bond in the product.
3. Two additional C-C single bonds are formed between each terminal carbon of butadiene with each carbon of ethene to give a single product from two reactants.
4. Typical sp3-sp3 C-C bond length is 154 pm while sp3-sp2 C-C bonds are 150 pm. These are consistent with the bond lengths in the product.
5. The Van der Waals radius of carbon is 170 pm. The interatomic distances between carbon atoms at reaction centres in the transition state are shorter than the Van der Waals radius. This indicates that the carbon atoms approach each other to undergo a reaction.

Vibrations

Imaginary Frequency	Lowest Positive Frequency
Table 3.

The Imaginary Frequency above illustrates the vibrational mode leading to the transition state of the reaction. It can be seen that this vibration involves stretching that elongates all three C=C bonds with a simultaneous shortening of the C-C bond in butadiene. This corresponds exactly to the expected change in bond lengths according to the reaction as detailed above. This vibration also has an out-of-plane bend involving the atoms involved in the reaction centre. Namely, each terminal carbon atom of butadiene is brought closer to each carbon atom of ethene leading to bond formation. The lowest positive frequency involves in plane bendings and does not lead to a reaction.

Animation of Reaction Coordinate	Energy Curve
Table 4.

The reaction proceeds via a synchronous formation of bonds. This can be seen in the animation of the reaction coordinate above. Furthermore, the presence of a single maximum in the potential energy curve reinforces this.

Nf710 (talk) 23:52, 15 December 2016 (UTC) A good first exercise everything was answered fairly well. you could have talked about the demand of the reaction

Exercise 2

MO Analysis

		Cyclohexadiene	1,3-dioxole	TS	Product
Endo	HOMO	Antisymmetric	Symmetric
Endo	2nd HOMO
Endo	LUMO	Symmetric	Antisymmetric
Endo	2nd LUMO
Exo	HOMO	Antisymmetric	Symmetric
Exo	2nd HOMO
Exo	LUMO	Symmetric	Antisymmetric
Exo	2nd LUMO
Table 5. Illustrations of key MOs

(This is a pretty huge table. Quite difficult to compared each without scrolling a lot. This page is also using nearly 1GB of memory and ~30% CPU! You should cut back on the number of antialiased Jmols Tam10 (talk) 11:07, 12 December 2016 (UTC))

For both exo and endo products, it can be seen that the HOMO of the dienophile (1,3 diaxole) and LUMO of the diene (cyclohexadiene) are both symmetric. This common symmetry allows them to overlap to form the HOMO of LUMO in the transition state. The LUMO of the dienophile (1,3 diaxole) and HOMO of the diene (cyclohexadiene) are both antisymmetric. This common symmetry allows them to overlap to form the 2nd HOMO and 2nd LUMO in the transition state.

It can be seen that the HOMO and LUMO of the TS are symmetric and therefore must be formed by overlap between symmetric orbitals from the diene and dienophile. The HOMO of the dienophile (1,3 diaxole) and LUMO of the diene (cyclohexadiene) are symmetric therefore these are the orbitals that overlap to form the HOMO and LUMO of the TS. By definition, an inverse-electron demand Diels-Alder reaction is one where the electrons are provided by the dienophile. Since the filled HOMO of our dienophile (1,3 diaxole) overlaps with the unfilled LUMO of our diene (cyclohexadiene) in the reaction, it can be concluded that this is an inverse-electron demand Diels-Alder reaction.

In a normal electron demand Diels-Alder reaction, the LUMO of the dienophile will be comparable in energy to the HOMO of the diene. Hence, these are the orbitals that will overlap in the reaction. However, in this case, the electron donating oxygen atoms in 1,3 diaxole raises the energy of its HOMO, making it comparable in energy to the LUMO of our diene (cyclohexadiene) resulting in overlap between them. This is the origin for the inverse electron demand reaction.

Thermochemical Analysis

Nf710 (talk) 00:18, 16 December 2016 (UTC)B3LYP Energies correct well done.

The sum of electronic and thermal Free Energies (Hartree)
	Cyclohexadiene	1,3-dioxole	Reactants	Transition State	Products	Energy barrier	Reaction energy
Endo	-233.324374	-267.068642	-500.393016	-500.332148	-500.418692	0.060868	-0.025676
Exo	-233.324374	-267.068642	-500.393016	-500.329165	-500.417321	0.063851	-0.024305
Table 6. Values of the sum of electronic and thermal Free Energies in Hartree units obtained with calculation using the DFT method)

The sum of electronic and thermal Free Energies (kJ/mol)
	Cyclohexadiene	1,3-dioxole	Reactants	Transition State	Products	Energy barrier	Reaction energy
Endo	-612593.190602	-701188.772985	-1313781.96359	-1313622.15464	-1313849.37593	159.808946	-67.41234314
Exo	-612593.190602	-701188.772985	-1313781.96359	-1313614.32277	-1313845.77637	167.640813	-63.81278236
Table 7. Values of the sum of electronic and thermal Free Energies in kJ/mol obtained with calculation using the DFT method)

The same reactants react via separate reaction pathways to give two different products. The kinetic product is the product formed via the pathway involving the lower activation energy or reaction barrier. The configuration with lowest energy is the thermodynamic product. It can be seen from table 7. that the endo configuration represents both the thermodynamic and kinetic product. The endo one is the kinetic product because of its lower energy barrier of 159.808946 kJ/mol v.s 167.640813 kJ/mol for the exo reaction. The endo product also has a lower energy than the exo product, resulting in a more negative reaction energy since both reactions utilise the same reactants making it the thermodynamic product.

The lower activation energy for the endo pathway can be attributed to secondary orbital interactions between the p-orbitals of both oxygen atoms on 1,3-dioxole and the pi* system of the cyclohexadiene involving the two carbon atoms adjacent to the sigma-bond forming carbon centres. This can clearly be seen in the HOMO of the endo transition state but is notably absent in the exo transition state HOMO in table 5.

The higher exo product energy can be attributed to a steric clash between the hydrogen atoms on the sp3 carbons of the 1,3-dioxole fragment with the hydrogen atoms on the sp3 carbons on the cyclohexadiene fragment directly above them. This also contributes to an elevation in the transition state energy due to a more unfavourable approach trajectory. This destabilising interaction is notably absent in the endo form as the aforementioned hydrogen atoms are not directly above one another.

00:24, 16 December 2016 (UTC) This sectionw as done well correct deduction of sterics and SSO giving the ordering of the reaction energies, dont uses as many Jmols

Exercise 3: Diels-Alder vs Cheletropic

Adducts and Transition States of the Xylylene-SO2 Diels-Alder and Chelotropic Reactions
		Adduct	Transition state
Diels-Alder	Endo
Diels-Alder	Exo
Chelotropic
Table 8.

("Adduct" refers to the products Tam10 (talk) 11:07, 12 December 2016 (UTC))

Intrinsic Reaction Coordinate

Endo Diels-Alder reaction
Forward endo Diels-Alder path	IRC curve of endo Diels-Alder reaction

Exo Diels-Alder reaction
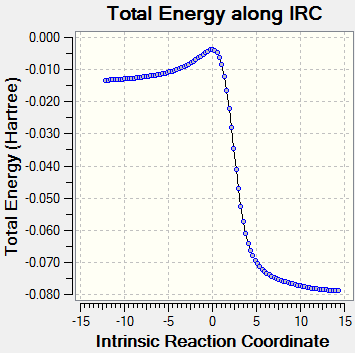
Forward exo Diels-Alder path	IRC curve of exo Diels-Alder reaction

Cheletropic Reaction
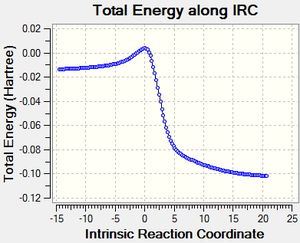
Forward cheletropic path	IRC curve of cheletropic reaction

Thermochemical Analysis

The sum of electronic and thermal Free Energies (Hartree)
	Xylylene	SO2	Reactants	Transition State	Products	Energy barrier	Reaction energy
Endo	0.178074	-0.119269	0.058805	0.090560	0.021702	0.031755	-0.037103
Exo	0.178074	-0.119269	0.058805	0.092075	0.021454	0.03327	-0.037351
Cheletropic	0.178074	-0.119269	0.058805	0.099062	0.000001	0.040257	-0.058804

The sum of electronic and thermal Free Energies (kJ/mol)
	Xylylene	SO2	Reactants	Transition State	Products	Energy barrier	Reaction energy
Endo	467.533323	-313.1407834	154.392539	237.765298	56.9786053	83.3727589	-97.41393392
Exo	467.533323	-313.1407834	154.392539	241.742931	56.3274813	87.350392	-98.06505797
Cheletropic	467.533323	-313.1407834	154.392539	260.087301	0.0026255002	105.694762	-154.3899138

The kinetic product was the endo product as it had the lowest activation energy. The thermodynamic product is the one which was obtained via the cheletropic reaction as this had the lowest reaction energy. The instability of xylylene is evident in its high free energy.

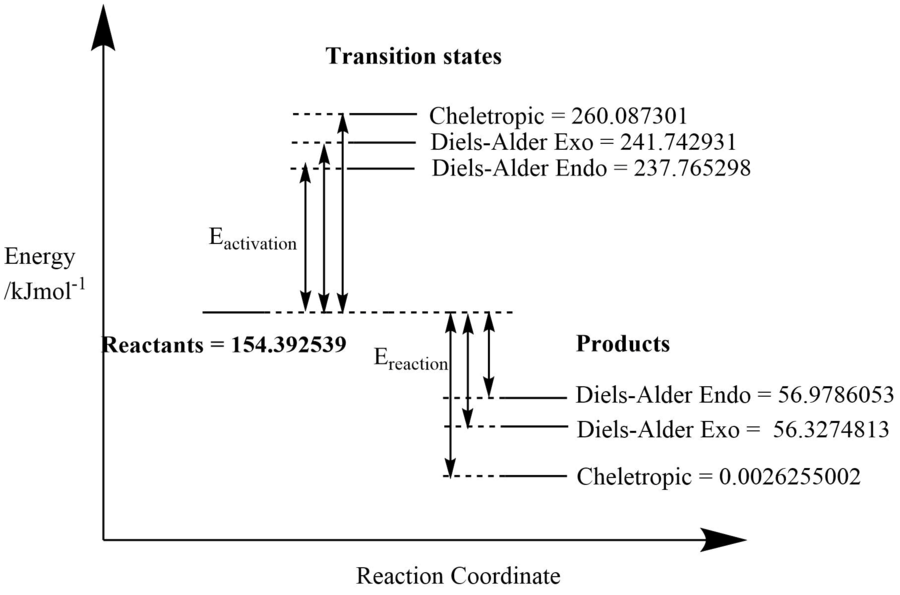
Reaction Profile showing relative heights of energy levels.

(It's much easier to read a reaction profile that's normalised. Usually the common point (reactants) are set to zero to allow quick comparison Tam10 (talk) 11:07, 12 December 2016 (UTC))

Throughout the course of the reaction as viewed from the IRC animation, it can be seen that the two exocyclic C=C bonds lengthen and are converted into C-C bonds. The six-membered ring then gains a C=C bond to form a benzene like structure with six delocalised pi-electrons conveying resonance.

Second Butadiene Reaction Site

Reaction	Endo	Exo

The sum of electronic and thermal Free Energies (kJ/mol)
	Xylylene	SO2	Reactants	Transition State	Products	Energy barrier	Reaction energy
Endo	467.533323	-313.1407834	154.392539	267.987431	172.259068	113.594892	17.866529
Exo	467.533323	-313.1407834	154.392539	275.819298	176.706665	121.426759	22.314126

It can be seen from the significantly greater reaction barriers that a Diels-Alder reaction at this second cis-butadiene fragment within o-xylylene is kinetically unfavourable. In addition, the products were of greater energy than the reactants giving a positive reaction energy, i.e this is an endothermic reaction. Hence, this reaction is thermodynamically unfavourable as well.

Conclusion

In this computational lab, three methods were introduced to optimise transition state structures. The first two involved guessing of the transition structure based on chemical intuition and knowledge about the reaction beforehand. While these methods were generally simpler, often less than satisfactory structure would be obtained even for the small chemical systems in the exercises. The third method involves more effort as it requires starting from the products or reactants then working backwards or forwards to the transition structure. The principle of this method is not unlike Hammond's postulate. Optimisation using this method can be tricky if the transition structure is dissimilar from the products or reactants.

These methods were applied to several cycloaddition reactions with increasing complexity and a cheletropic reaction. Molecular orbitals were generated which allowed visualisation of key MOs involved in these reactions. The exercises also informed about the trade-offs between accuracy and time in computational chemistry as more sophisticated calculations such as DFT require a significantly greater amount of time and computational power.