Rep:Dy815

Introduction

Potential Energy Surface (PES)

The Potential energy surface (PES) is a central concept in computational chemistry, and PES can allow chemists to work out mathematical or graphical results of some specific chemical reactions.

The concept of PES is based on Born-Oppenheimer approximation - in a molecule the nuclei are essentially stationary compared with the electrons motion, which makes molecular shapes meaningful.

The potential energy surface can be plotted by potential energy against any combination of degrees of freedom or reaction coordinates; therefore, geometric coordinates, $q$, should be applied here to describe a reacting system. For example, as like Second Year molecular reaction dynamics lab (triatomic reacting system: HOF), geometric coordinate ($q_1$) can be set as O-H bond length, and another geometric coordinate ($q_2$) can be set as O-F bond length. However, as the complexity of molecules increases, more dimensions of geometric parameters such as bond angle or dihedral need to be included to describe these complex reacting systems. In this computational lab, $q$ is in the basis of the normal modes which are a linear combination of all bond rotations, stretches and bends, and looks a bit like a vibration.

Nf710 (talk) 09:38, 8 March 2018 (UTC) Well done you seem to have actually undertstood normal mode. you change from the basis of degrees of freedom to normals modes when you diagonalize the hessian matrix.

Transition State

Transition state is normally considered as a point with the highest potential energy in a specific chemical reaction. More precisely, for reaction coordinate, transition state is a stationary point (zero first derivative) with negative second derivative along the minimal-energy reaction pathway($\frac{dV}{dq}=0$ and $\frac{d^{2}V}{d{q}^2}<0$). $V$ indicates the potential energy, and $q$ here represents an geometric parameter, in the basis of normal modes at transition state, which is a linear combination of all bond rotations, streches and bends, and hence looks like a vibration.

In computational chemistry, along the geometric coordinates ($q$), one lowest-energy pathway can be found, as the most likely reaction pathway for the reaction, which connects the reactant and the product. The maximum point along the lowest-energy path is considered as the transition state of the chemical reaction.

Nf710 (talk) 09:41, 8 March 2018 (UTC) You get the second derivatives as the eigen values of the hessian when you diagonalise it. the eiegenvectors are the normal modes and these are the vibrations that you see when you move back and forth along the vector.

Computational Method

As Schrödinger equation states, $⟨\mathrm{\Psi }|\mathbf{H}|\mathrm{\Psi }⟩=⟨\mathrm{\Psi }|\mathbf{E}|\mathrm{\Psi }⟩,$ a linear combination of atomic orbitals can sum to the molecular orbital: $\sum _i^N{c}_i|\mathrm{\Phi }⟩=|\psi ⟩.$ If the whole linear equation expands, a simple matrix representation can be written:

$$\begin{gathered} E=\left(\begin{array}{cccc}{c}_1& c_2& \cdots & \\ {c}_i\end{array}\right)\left(\begin{array}{cccc}⟨{\mathrm{\Psi }}_1|\mathbf{H}|{\mathrm{\Psi }}_1⟩& ⟨{\mathrm{\Psi }}_1|\mathbf{H}|{\mathrm{\Psi }}_2⟩& \cdots & ⟨{\mathrm{\Psi }}_1|\mathbf{H}|{\mathrm{\Psi }}_i⟩\\ ⟨{\mathrm{\Psi }}_2|\mathbf{H}|{\mathrm{\Psi }}_1⟩& ⟨{\mathrm{\Psi }}_2|\mathbf{H}|{\mathrm{\Psi }}_2⟩& \cdots & ⟨{\mathrm{\Psi }}_2|\mathbf{H}|{\mathrm{\Psi }}_i⟩\\ ⋮& ⋮& \ddots & ⋮\\ ⟨{\mathrm{\Psi }}_i|\mathbf{H}|{\mathrm{\Psi }}_1⟩& ⟨{\mathrm{\Psi }}_i|\mathbf{H}|{\mathrm{\Psi }}_2⟩& \cdots & ⟨{\mathrm{\Psi }}_i|\mathbf{H}|{\mathrm{\Psi }}_i⟩\\ \end{array}\right)\left(\begin{array}{c}{c}_1\\ c_2\\ ⋮\\ c_i\end{array}\right), \end{gathered}$$

where the middle part is called Hessian matrix.

Nf710 (talk) 09:42, 8 March 2018 (UTC) Hamiltonian Matrix!

Therefore, according to variation principle in quantum mechanics, this equation can be solve into the form of $H_c$ = $E_c$.

In this lab, GaussView is an useful tool to calculate molecular energy and optimize molecular structures, based on different methods of solving the Hessian matrix part ($H_c$ bit in the simple equation above). PM6 and B3LYP are used in this computational lab, and main difference between PM6 and B3LYP is that these two methods use different algorithms in calculating the Hessian matrix part. PM6 uses a Hartree–Fock formalism which plugs some empirically experimental-determined parameters into the Hessian matrix to simplify the molecular calculations. While, B3LYP is one of the most popular methods of density functional theory (DFT), which is also a so-called 'hybrid exchange-correlation functional' method. Therefore, in this computational lab, the calculation done by parameterized PM6 method is always faster and less-expensive than B3LYP method.

Nf710 (talk) 09:44, 8 March 2018 (UTC) Good section, nice work with the formatting. It would have been good if you could have put some equations in there shown the difference between the 2 methods.

Exercise 1

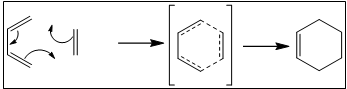
In this exercise, very classic Diels-Alder reaction between butadiene and ethene has been investigated. In the reaction, an acceptable transition state has been calculated. The molecular orbitals, comparison of bond lengths for different C-C and the requirements for this reaction will be discussed below. (The classic Diels-Alder reaction is shown in figure 1.)

Note : all the calculations were at PM6 level.

Figure 1. Reaction Scheme of Diels Alder reaction between butadiene and ethene

Molecular Orbital (MO) Analysis

Molecular Orbital (MO) diagram

The molecular orbitals of Diels-Alder reaction between butadiene and ethene is presented below (Fig 2):

Figure 2. MO diagram of Diels Alder reaction between butadiene and ethene

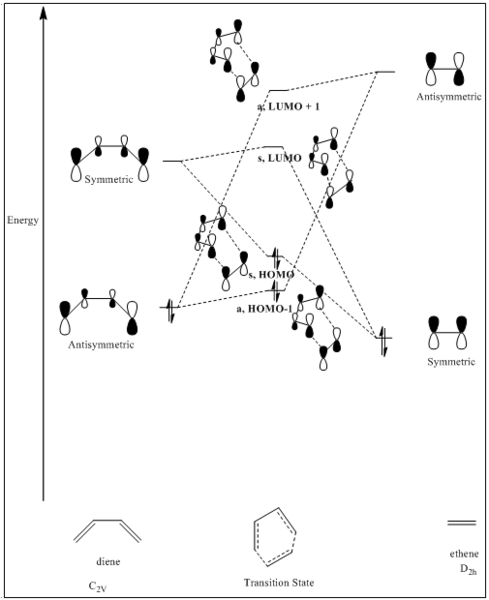
In figure 2, all the energy levels are not quantitatively presented because GaussView is not able to give very accurate energies. It is worth noticing that the energy level of ethene LUMO is the highest among all MOs, while the energy level of ethene HOMO is the lowest one. To confirm the correct order of energy levels of MO presented in the diagram, energy calculations at PM6 level have been done, and Jmol pictures of MOs have been shown in table 1 (from low energy level to high energy level):

table 1: Table for energy levels of MOs in the order of energy(from low to high)

ethene HOMO - MO 31	butadiene HOMO - MO 32	transition state HOMO-1 - MO 33	transition state HOMO - MO 34	butadiene LUMO - MO 35	transition state LUMO - MO 36	transition state LUMO+1 - MO 37	ethene LUMO - MO 38

In table 1, all the calculations are done by putting the reactants and the optimized transition state in the same PES. TO achieve this, all the components (each reactant and the optimized transition state) are set a far-enough distances to avoid any presence of interactions in this system (the distance usually set up greater than 6 Å, which is greater than 2 × Van der Waals radius of atoms). The pictures of calculation method and molecular buildup are presented below:

Figure 3. energy calculation method for MOs

Figure 4. molecular buildup for MO energy calculation

Frontier Molecular Orbital (FMO)

The table 2 below contains the Jmol pictures of frontier MOs - HOMO and LUMO of two reactants (ethene and butadiene) and HOMO-1, HOMO, LUMO and LUMO+1 of calculated transition state are tabulated.

(Fv611 (talk) Unfortunately, you did not optimise butadiene (the log file you include is not an optimisation but a frequency calculation). This error carried through to the MO, where you got the wrong relative energy for the butadiene LUMO.)

table 2: Table of HOMO and LUMO of butadiene and ethene, and the four MOs produced for the TS

Molecular orbital of ethene (HOMO)	Molecular orbital of ethene (LUMO)
Molecular orbital of butadiene (HOMO)	Molecular orbital of butadiene (LUMO)
Molecular orbital of TS (HOMO-1)	Molecular orbital of TS (HOMO)
Molecular orbital of TS (LUMO)	Molecular orbital of TS (LUMO+1)

Requirements for successful Diels-Alder reactions

Combining with figure 2 and table 2, it can be concluded that the requirements for successful reaction are direct orbital overlap of the reactants and correct symmetry. Correct direct orbital overlap leads to a successful reaction of reactants with the same symmetry (only symmetric/ symmetric and antisymmetric/ antisymmetric are 'reaction-allowed', otherwise, the interactions are 'reaction-forbidden'). As a result, the orbital overlap integral for symmetric-symmetric and antisymmetric-antisymmetric interactions is non-zero, while the orbital overlap integral for the antisymmetric-symmetric interaction is zero.

Measurements of C-C bond lengths involved in Diels-Alder Reaction

Measurements of 4 C-C bond lengths of two reactants and bond lengths of both the transition state and the product gives the information of reaction. A summary of all bond lengths involving in this Diels-Alder reaction has been shown in the figure 5 and corresponding dynamic pictures calculated by GaussView are also shown below (figure 6):

Figure 5. Summary of bond lengths involving in Diels Alder reaction between butadiene and ethene

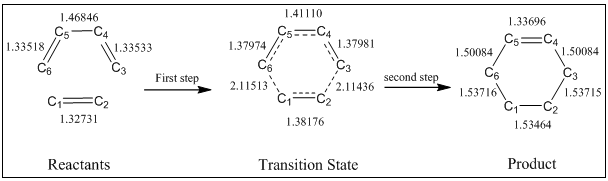
Figure 6. Corresponding (to figure 5) dynamic Jmol pictures for C-C bond lengths involving in Diels Alder reaction

The change of bond lengths can be clearly seen in figure 5, in first step, the double bonds in ethene (C₁-C₂) and butadiene (C₃-C₄ and C₅-C₆) increase from about 1.33Å to about 1.38Å, while the only single bond in butadiene (C₄-C₅) is seen a decrease from 1.47Å to 1.41Å. Compared to the literature values of C-C (sp³:1.54Å), C=C (sp²:1.33Å) and Van der Waals radius of carbon (1.70Å), the changes of bond lengths indicate that C=C(sp²) changes into C-C(sp³), and C-C(sp³) changes into C=C(sp²) at the meantime. As well, since the C₁-C₆ and C₂-C₃ is less than twice fold of Van der Waals radius of carbon (~2.11Å < 3.4Å), the orbital interaction occurs in this step as well. Because all other C-C bond lengths (except C₁-C₆ and C₂-C₃) are greater than the literature value of C=C(sp²), and less than the literature value of C-C(sp³), all the C-C bonds can possess the properties of partial double bonds do.

After the second step, all the bond lengths in the product (cyclohexene) go to approximately literature bond lengths which they should be.

Vibration analysis for the Diels-Alder reaction

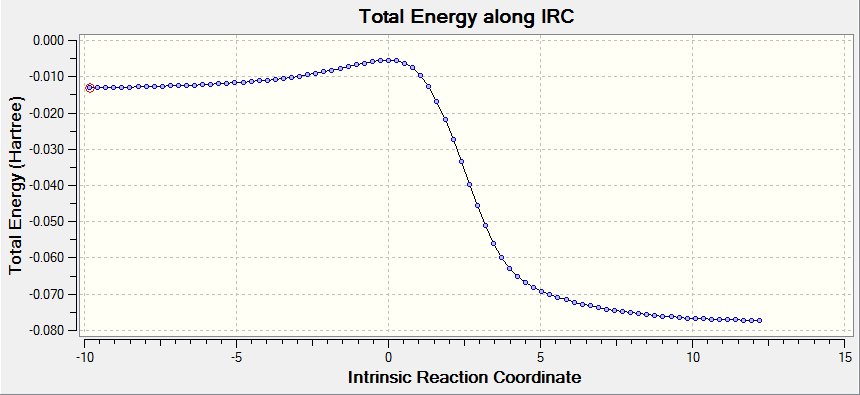
(Fv611 (talk) This is not a gif of the vibration, but a movie of the IRC.)

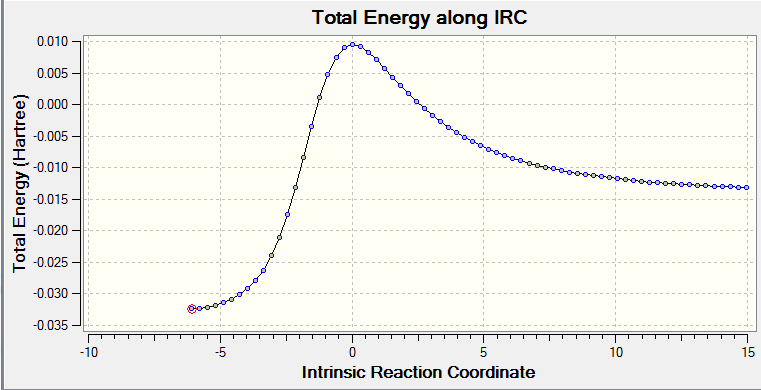
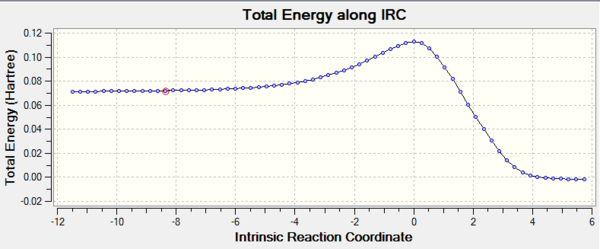
The vibrational gif picture which shows the formation of cyclohexene picture is presented below (figure 7):

Figure 7. gif picture for the process of the Diels-Alder reaction

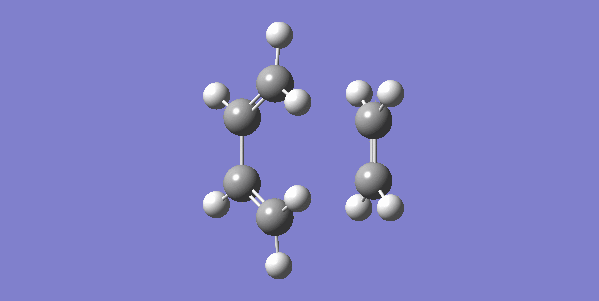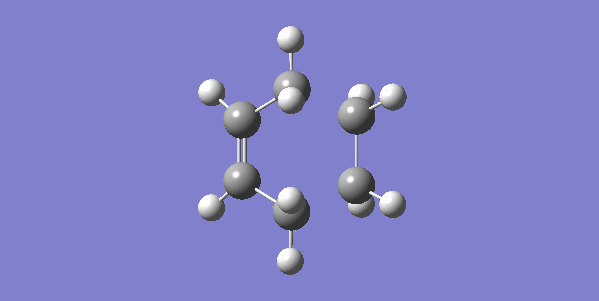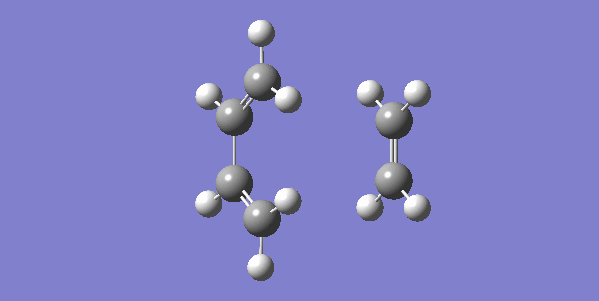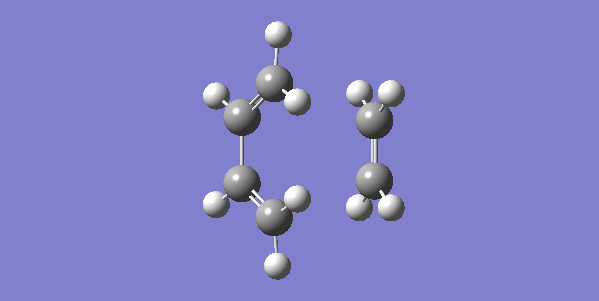
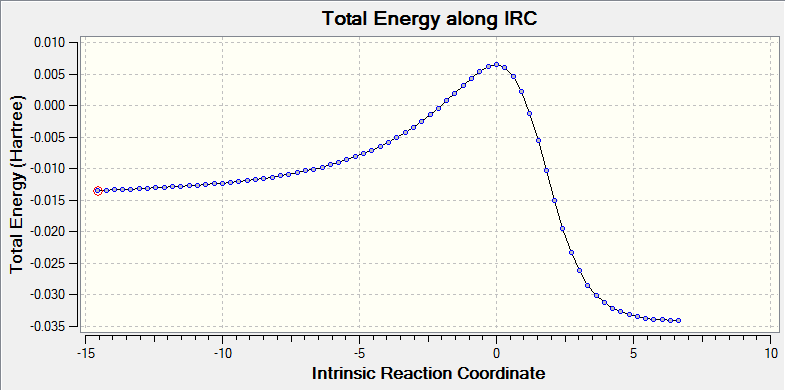
In this gif, it can also be seen a synchronous process according to this vibrational analysis. So, GaussView tells us that Diels-Alder reaction between ethane and butadiene is a concerted pericyclic reaction as expected. Another explanation of a synchronous process is that in molecular distance analysis at transition state, C₁-C₆ = C₂-C₃ = 2.11 Å.

In the gif, we can also see that these two reactants approach each other with their π orbitals parallel head to head, p orbitals for the ends of both reactants dis-rotated to form two new sigma bonds symmetrically. This is supported by Woodward–Hoffmann rules which states a [4+2] cycloadditon reaction is thermally allowed.

Additionally, IRC energy graph for this vibrational analysis is plotted as well (figure 7*).

Figure 7* IRC energy graph

Calculation files list

optimized reactant: Media:EX1 SM1 JMOL.LOG Media:DY815 EX1 DIENE.LOG

optimized product: Media:PRO1-PM6(FREQUENCY).LOG

otimized/frequency calculated transition state:Media:DY815 EX1 TSJMOL.LOG

IRC to confirm the transition state: Media:DY815-EX1-IRC-PM6.LOG

Energy calculation to confirm the frontier MO: Media:DY815 EX1 SM VS TS ENERGYCAL.LOG

Exercise 2

Figure 8. Reaction scheme for Diels-Alder reaction between cyclohexadiene and 1,3-dioxole

The reaction scheme (figure 8) shows the exo and endo reaction happened between cyclohexadiene and 1,3-dioxole. In this section, MO and FMO are analyzed to characterize this Diels-Alder reaction and energy calculations will be presented as well.

Note:All the calculations in this lab were done by B3LYP method on GaussView.

Molecular orbital at transition states for the endo and exo reaction

(Fv611 (talk) You end up with the correct MO diagrams, but you should have been able to reach the same conclusion with an analysis of the reactants and TS separately.)

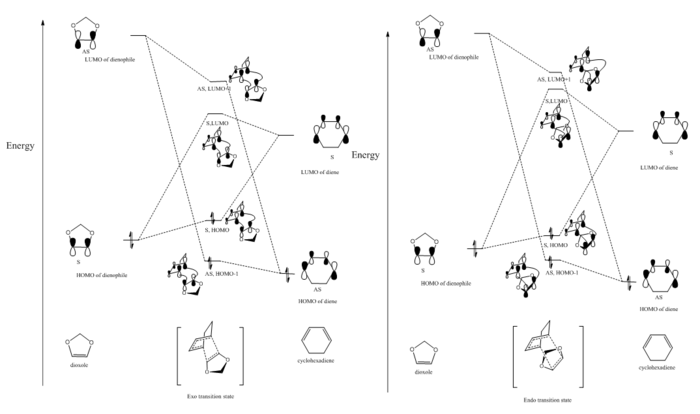
Correct MOs of the Exo Diels-Alder reaction, generated by energy calculation

The energy calculation for the exo transition state combined with reactants has been done in the same PES. The distance between the transition state and the reactants are set far away to avoid interaction between each reactants and the transition state. The calculation follows the same energy calculation method mentioned in fig 3 and fig 4, except B3LYP method being applied here. Table 3 includes all the MOs needed to know to construct a MO diagram.

table 3: Table for Exo energy levels of TS MO in the order of energy(from low to high)

cyclohexadiene HOMO - MO 79	EXO TS HOMO-1 - MO 80	1,3-dioxole HOMO - MO 81	EXO TS HOMO - MO 82	cyclohexadiene LUMO - MO 83	EXO TS LUMO - MO 84	EXO TS LUMO+1 - MO 85	1,3-dioxole LUMO - MO 86

Figure 9. MO for exo Diels-Alder reaction between cyclohexadiene and 1,3-dioxole

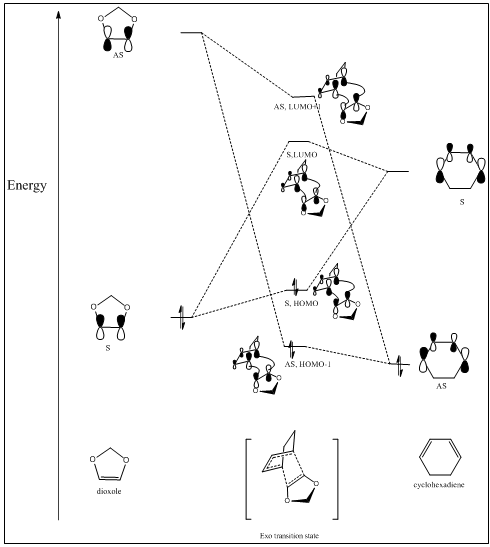
Therefore, the MO diagram can be constructed as above (figure 9). Note: all the energy levels are not quantitatively presented because GaussView is not able to give very accurate energies.

Incorrect MO diagram of the Endo Diels-Alder reaction, genereated by energy calculation

The determination of endo MO here follows the exactly same procedures as mentioned in construction exo MO, except substituting the endo transition into exo transition state. Table 4 shows the information needed to construct endo MO.

table 4: Table for Endo energy levels of TS MO (energy from low to high)

1,3-dioxole HOMO - MO 79	ENDO TS HOMO-1 - MO 80	ENDO TS HOMO - MO 81	cyclohexadiene HOMO - MO 82	cyclohexadiene LUMO - MO 83	1,3-dioxole LUMO - MO 84	ENDO TS LUMO - MO 85	ENDO TS LUMO+1 - MO 86

Based on the table above, the MO diagram for endo can be generated (figure 10) because all the relative energy levels are clearly seen. Note: all the energy levels are not quantitatively presented because GaussView is not able to give very accurate energies.

Figure 10. Wrong MO for endo Diels-Alder reaction between cyclohexadiene and 1,3-dioxole

This MO diagram was not what we expected because the LUMO of dienophile should be higher than the unoccupied orbitals of endo transition state as like as exo MO. This is not correct. Therefore, a new method to determine endo transition state was done.

Correct for the Endo MO diagram, with calculating combined endo and exo transition states and reactants

The new comparison method follows:

• Putting two transition states (endo and exo) in a single Guassview window with far enough distance to avoid any interaction. Far enough means the distance > 2 * VDW radius of carbon.

• Putting 1,3-dioxole and cyclohexadiene in the same Guassview window with far enough distance to avoid any interaction.

• Make sure these four components have no interaction with each other. Putting these four components in one GaussView window is to make sure these components being calculated on the same PES.(The final setup shown below)

Putting the four components together

• Calculate energy at B3LYP level (as shown in figures below).

energy calculation for the system

B3LYP calculation method being appiled

• The obtained MO is shown below:

12 desired MOs generated to obtain the correct MO

Although the relative molecular orbitals were obtained, the log file for the calculation is greater than 8M (actually 9367KB). Even though it was impossible to upload it in wiki file, a table (Table 5) which shows relations for these MOs is presented below.

table 5: Table for energy levels of transition states (Exo and Endo) MO and reactants MO

MO-118	MO-119	MO-120	MO-121	MO-122	MO-123	MO-124	MO-125	MO-126	MO-127	MO-128	MO-129
cyclohexadiene HOMO	EXO TS HOMO-1	ENDO TS HOMO-1	1,3-dioxole HOMO	ENDO TS HOMO	EXO TS HOMO	cyclohexadiene LUMO	EXO TS LUMO	ENDO TS LUMO	EXO TS LUMO+1	ENDO TS LUMO+1	1,3-dioxole LUMO

Therefore, the actually correct MO diagrams, containing both endo and exo transition states molecular orbitals, was presented and shown below (shown in figure 10*). Note: all the energy levels are not quantitatively presented because GaussView is not able to give very accurate energies.

Figure 10*. Correct MO diagram for endo TS

From table (table 5) above, the difference between exo TS and endo TS is not clearly seen. If we calculate these two transition states (endo and exo) in the same PES together, we can see clearly from the table below (table 6) that the energy levels of HOMO-1, LUMO and LUMO+1 for Exo TS are lower than these energy levels of Endo MO, while HOMO for Exo TS is higher comapared to HOMO for Endo TS. Because the log file with two transition states only is smaller than 8M, the Jmol pictures are able to be uploaded to wiki file and tabulated (table 6).

table 6: Table for Exo and Endo energy levels of TS MO in the order of energy(from low to high)

EXO TS HOMO-1 - MO 79	ENDO TS HOMO-1 - MO 80	ENDO TS HOMO - MO 81	EXO TS HOMO - MO 82	EXO TS LUMO - MO 83	ENDO TS LUMO - MO 84	EXO TS LUMO+1 - MO 85	ENDO TS LUMO+1 - MO 86

Characterize the type of DA reaction by comparing dienophiles in EX1 and EX2 (ethene and 1,3-dioxole)

This Diels Alder reaction can be characterized by analysing the difference between molecular orbitals for dienophiles, because the difference for two diene (butadiene vs cyclohexadiene) is not big and we cannot decide the type of DA reaction by comparing the dienes.

table 7: Table for Exo energy levels of TS MO in the order of energy(from low to high)

ethene HOMO - MO 26	1,3-dioxole HOMO - MO 27	ethene LUMO - MO 28	1,3-dioxole LUMO - MO 29

To confirm the which type of Diels-Alder reaction it is, we need to put the two reactants on the same PES to compare the absolute energy, which can be done by GaussView energy calculation. The procedures are very similar to exercise 1 (figure 3, figure 4) - put two reactants in the same window, setting a far enough distance to avoid any interaction, and then use energy calculation at B3LYP level.

Table 8: table of energy calculation resulted in this DA reaction

	HOMO	LUMO	Energy difference (absolute value)
standard	cyclohexadiene	1,3-dioxole	0.24476 a.u.
inverse	1,3-dioxole	cyclohexadiene	0.17774 a.u

It can be concluded from the table that it is an inverse electron demand Diels-Alder reaction, because energy difference for inverse electron demand is lower than the standard one. This is caused by the oxygens donating into the double bond raising the HOMO and LUMO of the 1,3-dioxole. Due to the extra donation of electrons, the dienophile 1,3-dioxole, has increased the energy levels of its HOMO and LUMO.

Nf710 (talk) 11:02, 8 March 2018 (UTC) You have clearly put lots of effort in here to try and understand the electron demand of the reaction. I struggled to follow it at times. But I see that you have done a nice comparisions between the energy gap between the FMOs of the reactants with a single point energy calculation. well done.

Reaction energy analysis

calculation of reaction energies

table 9. thermochemistry data from Gaussian calculation

	1,3-cyclohexadiene	1,3-dioxole	endo-transition state	exo-transition state	endo-product	exo-product
Sum of electronic and free energies at 298k (Hartree/Particle)	-233.324374	-267.068643	-500.332150	-500.329165	-500.418692	-500.417321
Sum of electronic and free energies at 298k (KJ/mol)	-612593.1906	-701188.77561	-1313622.1599	-1313614.3228	-1313849.3759	-1313845.7764

The reaction barrier of a reaction is the energy difference between the transition state and the reactant. If the reaction barrier is smaller, the reaction goes faster, which also means it is kinetically favoured. And if the energy difference between the reactant and the final product is large, it means that this reaction is thermodynamically favoured.

table 10. Reaction energy and activation energy for endo and exo DA reaction

	reaction energy (KJ/mol)	activation energy (KJ/mol)
EXO	-63.81	167.64
ENDO	-67.41	159.81

We can see, from the table above, that endo pathway is not only preferred thermodynamically but also preferred kinetically. The reasons why it is not only thermodynamic product but also a kinetic product will be discussed later.

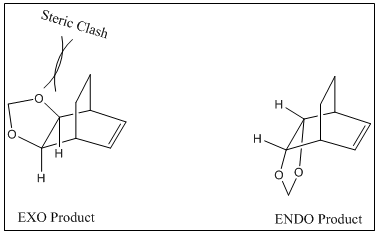
Steric clashes between bridging and terminal hydrogens

The reason why the endo product is the thermodynamic product can be rationalised by considering the steric clash in exo, which raises the energy level of exo product. Therefore, with the increased product energy level, the reaction energy for exo product is smaller than endo one.

Figure 11. different products with different steric clash

Secondary molecular orbital overlap

Figure 12. Secondary orbital effect

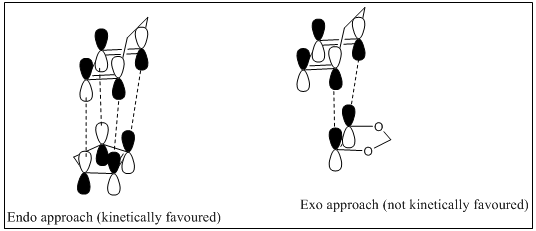
As seen in figure 12, the secondary orbital effect occurs due to a stablised transition state where oxygen p orbitals interact with π ^* orbitals in the cyclohexadiene. For exo transition state, only first orbital interaction occurs. This is the reason why endo product is the kinetic product as well.

table 11. Frontier molecular orbital to show secondary orbital interactions

ENDO TS MO of HOMO	EXO TS MO of HOMO

Table 11 gives the information of the frontier molecular orbitals.

Calculation files list

Energy calculation for the endo transition state combined with reactants has been done in the same PES:Media:DY815 EX2 ENDO MO.LOG

Energy calculation for the exo transition state combined with reactants has been done in the same PES:Media:DY815 EX2 EXO MO 2222.LOG

Frequency calculation of endo TS:Media:DY815 EX2 ENDO-TS2-B3LYP(FREQUENCY).LOG

Frequency calculation of exo TS:Media:DY815 EX2 TS2-B3LYP(FREQUENCY).LOG

Energy calculation for endo TS vs exo TS:Media:DY815 EX2 ENDOTS VS EXOTS ENERGYCAL.LOG

Energy calculation for EX1 dienophile vs EX2 dienophile:Media:DY815 COMPARISON FOR EX1 AND EX2 DIENOPHILE.LOG

Energy calculation for comparing HOMO and LUMO for cyclohexadiene vs 1,3-dioxole:Media:(ENERGY CAL GFPRINT) FOR CYCLOHEXADIENE AND 13DIOXOLE.LOG

Nf710 (talk) 11:33, 8 March 2018 (UTC) Good section you got the correct results and have made the correct conclusions, your diagrams are also very nice. You could have going into more detail about the kenetic and thermodynamic theory.

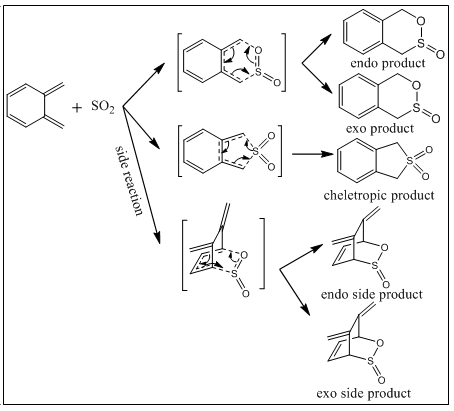
Exercise 3

In this section, Diels-Alder and its competitive reaction - cheletropic reaction will be investigated by using PM6 method in GaussView. Also, the side reactions - internal Diels-Alder and electrocyclic reaction will be discussed. The figure below shows the reaction scheme (figure 13).

Note: All the calculations done in this part are at PM6 level.

Figure 13. Secondary orbital effect

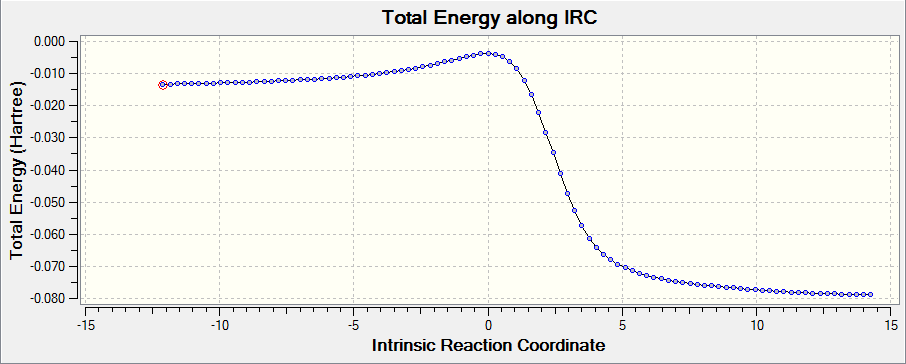
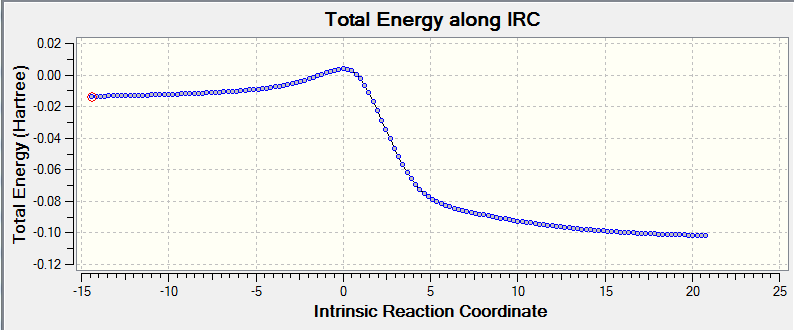
IRC calculation

IRC calculations use calculated force constants in order to calculate subsequent reaction paths following transition states. Before doing the IRC calculation, optimised products and transition states have been done. The table below shows all the optimised structures (table 12):

table 12: Table for optimised products and transition states

	endo Diels-Alder reaction	exo Diels-Alder reaction	cheletropic reaction
optimised product
optimised transition state

After optimising the products, set a semi-empirical distances (C-C: 2.2 Å) between two reactant components and freeze the distances. IRC calculations in both directions from the transition state at PM6 level were obtained. The table below shows IRC calculations for endo, exo and cheletropic reaction. As shown in the IRC gif, the six-member ring became the aromatic system during the reactions processing.

Table 13. IRC Calculations for reactions between o-Xylylene and SO₂

	Total energy along IRC	IRC
IRC of Diels-Alder reaction via endo TS
IRC of Diels-Alder reaction via exo TS
IRC of cheletropic reaction

Reaction barrier and activation energy

The thermochemistry calculations have been done and presented in the tables below:

table 14. Summary of electronic and thermal energies of reactants, TS, and products by Calculation PM6 at 298K

Components	Energy/Hatress	Energy/kJmol-1
SO2	-0.118614	-311.421081
Xylylene	0.178813	469.473567
Reactants energy	0.060199	158.052487
ExoTS	0.092077	241.748182
EndoTS	0.090562	237.770549
Cheletropic TS	0.099062	260.087301
Exo product	0.027492	72.1802515
Endo Product	0.021686	56.9365973
Cheletropic product	0.000002	0.0052510004

(Your xylylene energy is a bit too high. If you had included the log file for it we could have seen what happened Tam10 (talk) 11:11, 7 March 2018 (UTC))

The following figure and following table show the energy profile and the summary of activation energy and reaction energy.

Figure 14. Energy profile for ENDO, EXO and CHELETROPIC reaction

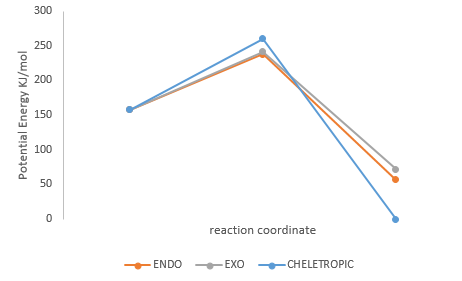
(You should include values on this diagram to make comparison easier. It's not immediately obvious which way around the profile is, so typically it's better to show where reactants/TS/products are as well. Excel is not the easiest program to do this with. Remember it doesn't need to be to scale if you have individual values on, so you can make it tidier if there's overlap Tam10 (talk) 11:11, 7 March 2018 (UTC))

table 15. Activation energy and reaction energy(KJ/mol) of three reaction paths at 298K

	Exo	Endo	Cheletropic
Activation energy (KJ/mol)	83.69570	79.71806	102.03481
Reaction energy (KJ/mol)	-85.87224	-101.11589	-158.04724

(Too many significant figures. The precision is an indication of trust and lack of error Tam10 (talk) 11:11, 7 March 2018 (UTC))

By calculation, the cheletropic can be considered as thermodynamic product because the energy gain for cheletropic pathway is the largest. The kinetic product, here, is endo product (the one with the lowest activation energy) just like as what was expected before.

Second Diels-Alder reaction (side reaction)

The second Diels-Alder reaction can occur alternatively. Also, for this second DA reaction, endo and exo pathways can happen as normal DA reaction do.

Figure 15. Second Diels-Alder reaction reaction scheme

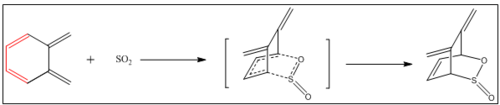
The table 16 below gives the IRC information and optimised transition states and product involved in this reaction:

Table 16. for TS IRC and optimised products for THE SECOND DA reaction between o-Xylylene and SO₂

	exo pathway for the second DA reaction	endo pathway for the second DA reaction
optimised product
TS IRC
Total energy along IRC

The table below (in table 17) gives the information of energies calculation:

table 17. Summary of electronic and thermal energies of reactants, TS, and products by Calculation PM6 at 298K

Components	Energy/Hatress	Energy/kJmol-1
SO2	-0.118614	-311.421081
Xylylene	0.178813	469.473567
Reactants energy	0.060199	158.052487
ExoTS (second DA reaction)	0.102070	267.984805
EndoTS (second DA reaction)	0.105055	275.821924
Exo product (second DA reaction)	0.065615	172.272196
Endo Product (second DA reaction)	0.067308	176.717167

The energy profile for the second Diels-Alder reaction is shown below (shown in figure 16):

figure 16. Energy profile for the second Diels-Alder reaction

And the activation energy and reaction energy for the second Diels-Alder reaction has been tabulated below. From this table, it can be concluded that the kinetic product is endo as expected, and the relative thermodynamic product here is endo as well.

table 18. Activation energy and reaction energy(KJ/mol) of second DA reaction paths at 298K

	Exo (for second DA reaction)	Endo (for second DA reaction)
Activation energy (KJ/mol)	109.93232	117.76944
Reaction energy (KJ/mol)	14.21971	18.66468

Comparing the normal Diels-Alder reaction and the second Diels-Alder reaction (side reaction)

figure 17. combined energy profile for five reaction pathways

(Perhaps keep the colours consistent throughout the exercise? Tam10 (talk) 11:11, 7 March 2018 (UTC))

As seen in figure 17, the combined energy profile has been shown to compare the activation energies and reaction energies. The energy profile illustrates that both endo and exo for second DA reaction is side reactions because their gain in reaction energy are both positive values. The positive values indicate that the second diels-Alder reactions are not thermodynamically favourable compared with the normal Diels-Alder reactions and cheletropic reaction. If we see the products formed by the second DA pathway, very distorted structures can be found, which means the products for the second DA pathway are not stablised.

The second DA reaction are not kinetically favourable, reflected by the activation energies for both side reaction pathways. The activation energies for side reaction are higher than the activation energies for other three normal reaction pathways (as shown in figure 17).

Some discussion about what else could happen (second side reaction)

Because o-xylyene is a highly reactive reactant in this case, self pericyclic reaction can happen photolytically.

figure 18. Electrocyclic rearrangement for reactive o-xylyene

While this reaction is hard to undergo under thermal condition because of Woodward-Hoffmann rules (this is a 4n reaction), this reaction can only happen only when photons are involved. In this case, this reaction pathway is not that kinetically competitive for all other reaction pathways, except the photons are involved.

In addition, in this side reaction, the product has a four-member ring, which means the product would have a higher energy than the reactant. This means this side reaction is also not that competitive thermodynamically.

(This is not true. You can perform the calculations to determine which is more stable. The important thing is whether it is kinetically viable. Tam10 (talk) 11:11, 7 March 2018 (UTC))

Calculation file list

Log file for CHELETROPIC IRC:Media:DY815-CHELETROPIC-IRC.LOG

Log file for CHELETROPIC PRODUCT:Media:DY815 EX3 CHELETROPIC-PRO1(FREQUENCY).LOG

Log file for CHELETROPIC TS:Media:DY815 EX3 CHELETROPIC-TS2(FREQUENCY).LOG

Log file for DIELS-ALDER ENDO IRC:Media:DY815 DIELS-ALDER- ENDO-IRC.LOG

Log file for DIELS-ALDER ENDO PRODUCT:[Media:DY815 EX3 DIELS-ALDER- ENDO-PRO1(FREQUENCY).LOG]]

Log file for DIELS-ALDER ENDO TS:Media:DY815 EX3 DIELS-ALDER- ENDO-TS2(FREQUENCY).LOG

Log file for DA EXO IRC:Media:Dy815-DIELS-ALDER- EXO-IRC.LOG

Log file for DA EXO PRODUCT:Media:DY815 EX3 DIELS-ALDER- EXO-PRO1(FREQUENCY).LOG

Log file for DA EXO TS:Media:DY815 EX3 DIELS-ALDER- EXO-TS2(FREQUENCY).LOG

Log file for SECOND DA IRC (ENDO):Media:INTERNAL-DIELS-ALDER-IRC(ENDO).LOG

Log file for SECOND DA IRC (EXO):Media:INTERNAL-DIELS-ALDER-IRC(EXO).LOG

Log file for SECOND DA PRODUCT (ENDO):Media:INTERNAL-DIELS-ALDER-P1(ENDO) (FREQUENCY).LOG

Log file for SECOND DA PRODUCT (EXO):Media:INTERNAL-DIELS-ALDER-P1(EXO).LOG

Log file for SECOND DA TS (ENDO):Media:INTERNAL-DIELS-ALDER-TS2(ENDO) (FREQUENCY).LOG

Log file for SECOND DA TS (EXO):Media:INTERNAL-DIELS-ALDER-TS2(EXO) (FREQUENCY).LOG

Conclusion

For all the works, GaussView shows reasonably good results, especially for predicting the reaction process.

In exercise 1 - Diels-Alder reaction between butadiene and ethene have been discussed, and in this exercise, necessary energy levels for molecular orbitals have been constructed and compared. Bond changes involved in the reaction have also been discussed, which illustrated that the reaction was a synchronous reaction.

In erexcise 2 - Diels-Alder reaction for cyclohexadiene and 1,3-dioxole, MOs and FMOs were constructed, followed by the energy calculations for the reaction. Although for working out endo MO diagram was a bit problematic by using individual energy calculation, it can be solved by constructing a non-interactive reactant-transition-state calculation. The MO diagram obtained is reasonably good, in terms of correct MO energies. In the last bit, via calculation, endo was determined as both kinetic and thermodynamic product.

In exercise 3 - reactions for o-xylyene and SO², the IRC calculations were presented to visualise free energy surface in intrinsic reaction coordinate at first. The calculation for each reaction energies were compared to show natures of the reactions.

For all calculation procedures, including all three exercises, products were firstly optimised, followed by breaking bonds and freezing these bonds at empirically-determined distances for specific transition states. The next step was to calculate 'berny transition state' of the components and then IRC was required to run to see whether the correct reaction processes were obtained.