Rep:Double Decker Chocolate Chip 'n Oreo Fudge Brownie Bar with Caramel Glaze
Matthew Wilfred Ho
Module 3
Cope Rearrangement
Reactants & Products

In this exercise, the Cope rearrangement of 1,5-hexadiene was investigated. Specifically, the energies of different conformers of the reactants, products, and transition states are calculated.
Optimisation
A total of ten different conformers of 1,5-hexadiene were drawn in Gaussview, and their structure cleaned before submission to Gaussian for structural optimisation using the Hartree-Fock method and 3-21g basis set. The table below summarizes the results, including a comparison of their relative energies: [1]
| Conformer | Structure | Point Group | Energy /Hartrees HF/3-21G |
Relative Energy /kcal mol-1 | |||
| Gauche 1 DOI:10042/to-13587 |
|
C2 | -231.68772 Summary |
3.10 | |||
| Gauche 2 DOI:10042/to-13588 |
|
C2 | -231.69167 Summary |
0.62 | |||
| Gauche 3 DOI:10042/to-13589 |
|
C1 | -231.69266 Summary |
0.00 | |||
| Gauche 4 DOI:10042/to-13590 |
|
C2 | -231.69153 Summary |
0.71 | |||
| Gauche 5 DOI:10042/to-13591 |
|
C1 | -231.68962 Summary |
1.91 | |||
| Gauche 6 DOI:10042/to-13592 |
|
C1 | -231.68916 Summary |
2.20 | |||
| Anti 1 DOI:10042/to-13593 |
|
C2 | -231.69260 Summary |
0.04 | |||
| Anti 2 DOI:10042/to-13594 |
|
Ci | -231.69254 Summary |
0.08 | |||
| Anti 3 DOI:10042/to-13595 |
|
C2h | -231.68907 Summary |
2.25 | |||
| Anti 4 DOI:10042/to-13596 |
|
C1 | -231.69097 Summary |
1.06 |
A comparison of the conformers' energies reveals Gauche 3 to be the stablest overall, and Anti 1 the second. Usually we would expect anti-conformers to be stabler than gauche conformers due to lower steric repulsion; however in the case of 1,5-hexadiene, a through-space interaction of the π bonds stabilises the structure in the Gauche 3 conformer. Otherwise, the anti conformers are generally of lower energy than the gauche conformers.
Frequency Analysis & Thermochemistry
The HF/3-21g level of theory is not sufficietly accurate for vibrational analysis. Instead, the DFT B3LYP/6-31g(d) optimised structure of the anti 2 conformer was subject to frequency analysis at two specific temperatures: 298.15 K and 0 K.
------------------- - Thermochemistry - ------------------- Temperature 298.150 Kelvin. Pressure 1.00000 Atm. Atom 1 has atomic number 6 and mass 12.00000 ... Zero-point correction= 0.142491 (Hartree/Particle) Thermal correction to Energy= 0.149847 Thermal correction to Enthalpy= 0.150791 Thermal correction to Gibbs Free Energy= 0.110881 Sum of electronic and zero-point Energies= -234.469212 Sum of electronic and thermal Energies= -234.461856 Sum of electronic and thermal Enthalpies= -234.460912 Sum of electronic and thermal Free Energies= -234.500822 ... Low frequencies --- -18.8141 -11.7180 0.0007 0.0008 0.0010 1.7521 Low frequencies --- 72.7146 80.1402 120.0114
------------------- - Thermochemistry - ------------------- Temperature 0.000 Kelvin. Pressure 1.00000 Atm. Atom 1 has atomic number 6 and mass 12.00000 ... Zero-point correction= 0.142928 (Hartree/Particle) Thermal correction to Energy= 0.142928 Thermal correction to Enthalpy= 0.142928 Thermal correction to Gibbs Free Energy= 0.142928 Sum of electronic and zero-point Energies= -234.468775 Sum of electronic and thermal Energies= -234.468775 Sum of electronic and thermal Enthalpies= -234.468775 Sum of electronic and thermal Free Energies= -234.468775 ... Low frequencies --- -18.8525 -11.7271 -0.0008 -0.0005 -0.0004 1.7534 Low frequencies --- 72.8032 80.2400 120.1763
A point to be noted is the rather large negative values present in low frequencies. This is undesirable since it represents translational motion of the molecule about its centre of mass, which should not be a consideration in vibrational analysis. Nevertheless, as these negative values could not be got rid of after several attempts, the analysis was carried through.
| 298.15 K DOI:10042/to-13598 |
0 K DOI:10042/to-13597 |
Remarks | |
| Sum of electronic and zero-point energies | -234.469212 Hartrees | -234.468775 Hartrees | E = Eelec + ZPE Potential energy at 0K. Expected not to vary from 0 to 298.15K due to the high energy involved in electronic excitation. |
| Sum of electronic and thermal energies | -234.461856 Hartrees | -234.468775 Hartrees | E = E + Evib + Etrans + Erot Energy at 298.15K and 1 atm. Includes vibrational, translational and rotational partition functions. |
| Sum of electronic and thermal enthalpies | -234.460912 Hartrees | -234.468775 Hartrees | H = E + RT Enthalpy term that accounts for thermal degrees of freedom ie. RT. |
| Sum of electronic and thermal free energies | -234.500822 Hartrees | -234.468775 Hartrees | G = H - TS Gibbs free energy, from which the contribution of entropy can be calculated. |
Note that all 4 terms are of equal value when computed at 0 Kelvin. This is to be expected, as thermal energy / enthalpy should have no contribution at absolute zero.
Transition State Structures
Allyl Fragment

In order to investigate the transition state for the Cope rearrangement, an allyl fragment was drawn in Gaussview and optimised using the HF/3-21g level of theory, resulting in a molecule with 0.139nm C-C bond length, and a C-C-C bond angle of 124.3°:
allyl |
Optimisation of Chair TS
TS(Berny) Optimisation
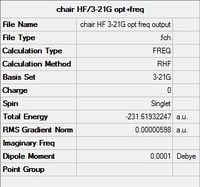
The chair transition state was constructed by pasting two allyl fragments into a rough chair conformation, with the terminal carbon atoms of each fragment set to 2.2 angstroms apart. This guess structure was then optimised using the TS(Berny) method to the HF/3-21G level. Instead of obtaining a structure with an energy minima, TS(Berny) optimises the structure to an energy maxima, whereby the transition state of the Cope rearrangement can be found. The additional keyword NoEigen was added to prevent the calculation from failing, in case the guess structure was not structurally similar enough to the transition state. Just as energy minimization may fail to find the global minima for regular optimizations, so too may the TS(Berny) method fail at finding the transition state, because not all maxima correspond to the desired transition state structure.
|
|
||||||
| Summary of HF/3-21g Optimisation | DOI:10042/to-13600 |
A review of the vibrational data reveals an imaginary frequency at -818 cm-1, as expected of the Cope Rearrangement, indicating the TS(Berny) optimisation had been performed successfully.
Frozen Coordinates
In using the Frozen Coordinates method, the Redundant Coordinate Editor was used to "freeze" the bond distances between the terminal carbons of the two allyl fragments to 2.2 angstroms as instructed. The keyword opt=ModRedundant is added automatically indicating that the bonds have been frozen - although other parameters such as bond angles or dihedral angles may be frozen as well, they are not explored within the scope of this exercise. The calculation is then set to a normal minimization via HF/3-21g; effectively the remaining parts of the molecule have their energy minimized, but maintaining the key bond being formed / broken during the transition state, which contributes most to its energy. This structure is then subjected to a TS(Berny) optimisation as with the above section.
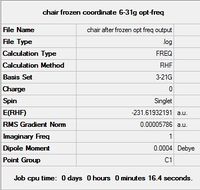
|
|
||||||
| Summary of Optimisation | DOI:10042/to-13601 |
Similarly, a review of the vibrational data reveals an imaginary frequency at -818 cm-1, again as expected of the Cope Rearrangement, indicating the Frozen Coordinate method had found the transition state structure.
Optimisation of Boat TS
For the Boat transition state, the QST2 method was used to find its structure. The method relies on both the reactant and product to be specified, such that Gaussian may then interpolate between the two structures and locate the transition state. For it to work though, it necessitates the correct numbering corresponding to both the reactant and product, and this was done as specified.

|
|
||||||
| Summary of Failed Optimisation | DOI:10042/to-13602 |
This optimisation resulted in failure. As is evident from the model, the cross-wise formation of C-C bonds is clearly impossible kinetically and energetically. The exceptionally high RMS Gradient norm value from the summary window also indicates a failure in optimisation. Further evidence of failure was found in the output file:
Item Value Threshold Converged? Maximum Force 0.028692 0.000450 NO RMS Force 0.004127 0.000300 NO Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES Predicted change in Energy= 0.000000D+00 Optimization aborted. -- No acceptable step.
The program could not find the transition state structure by interpolation of the given reactant / product. The problem lies with the inability of the method to rotate the central C-C bonds in finding the transition state. Instead, this step must be performed manually to make the reactant and product resemble the expected boat transition state more. To that end, the central C-C-C-C dihedral angle was modified to 0°, and the two central C-C-C bond angles altered to 100°:
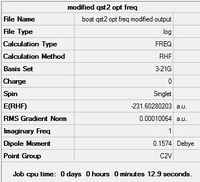 |
|
 |
|||||||
| Summary | DOI:10042/to-13648 |
Structural modification |
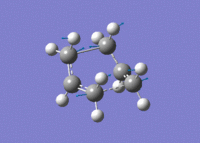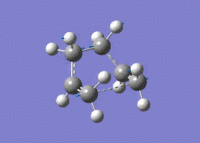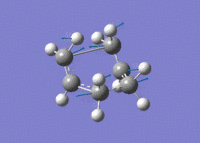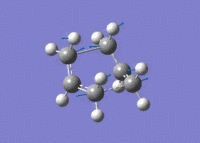
Again, an imaginary vibration at 840 cm-1 was found, providing further evidence that the correct transition state structure had been found.
Intrinsic Reaction Coordinate
The Intrinsic Reaction Coordinate is a method that makes incremental structural changes to a transition state, iteratively optimising the structure along a minimum energy path down the Potential Energy Surface (PES) to an energy minimum. Where the gradient of the PES is steepest indicates a minima. However, a transition state can go either backwards to the reactants, or forwards to the products. Therefore it is necessary to specify calculations in the forward direction to give the desired product structure. Two additional parameters can be specified: the number of steps, and the calculation of force constants, which can happen for:
1. every iteration,
2. only the initial one, or
3. not at all.
As always, the balance between accuracy and computational demands drive the decision to pick one choice of parameters over another, as we shall see in the investigation below.
For this exercise IRC was applied to the chair transition state. The following parameters were applied in the initial calculation:
# irc=(forward,maxpoints=50,calcfc) rhf/3-21g geom=connectivity
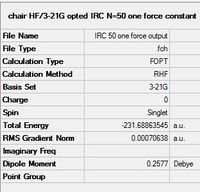
This specifies an IRC calculation using the Hartree-Fock method, 3-21g basis set in the forward direction, with a maximum of 50 iterations, and calculation of force constants for once only. The results are summarised as below:

|

|
|||
| Energy plot of IRC optimisation | RMS Gradient plot of IRC optimisation |
|
|
||||||
| Summary of Optimisation | DOI:10042/to-13685 |
The above data indicates that while optimisation has occurred, it had not gone to completion for the following reasons:
- The Total Energy along IRC curve is still sloping downward at the last step of optimisation, so the lowest energy conformation has not been reached.
- Similarly, the RMS gradient norm has not reached a stable minimum yet.
- As seen in the summary, the RMS Gradient norm value is 0.0007 a.u., which is higher than it should be if the structure has converged to a minimum.
- Although the structure of the last step of optimisation is clearly of a gauche conformation, it does not resemble any of the known stable conformers shown in the first section.
The evidence shows that the current parameters applied to the IRC method are insufficient for full optimisation. Therefore as follow-up, three different approaches were taken to remedy the situation:
- A new IRC calculation with force constants calculated at every step, keeping other parameters the same.
- Restarting the IRC calculation from the last structure, then specifying 100 steps, keeping other parameters the same
- Running a normal optimisation from the last structure.
| Modified method | Force constants calculated at every step | Restarting with 100 steps | Normal minimisation | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Optimised geometry |
DOI:10042/to-13717 |
DOI:10042/to-13718 |
DOI:10042/to-13719 | |||||||||
| Total Energy Plot |  |
 |
N/A | |||||||||
| RMS Gradient Plot | 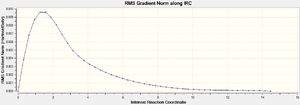 |
 |
N/A | |||||||||
| Summary | 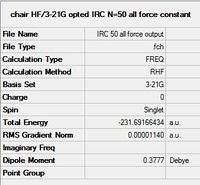 |
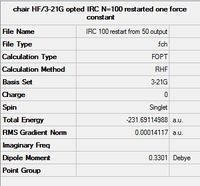 |
 | |||||||||
| Number of iterations | a | b | c | |||||||||
All three methods resulted in optimised structures of lower energy than the initial IRC calculation, corresponding to the Gauche 2 conformer. It should be noted that of the three methods, 100 additional calculation steps was the least effective, with the highest RMS Gradient Norm value at the last step. Methods 1 and 3, ie. calculate force constants at every step, and normal minimisation at the last step, producted very similar conformations with almost identical energies, showing that they are the better methods.
Activation Energy[2]
| Chair TS | Boat TS | |
| Sum of electronic and ZPE (298.15 K) /Hartree | -231.466700 | -231.450931 |
| Activation Energy (298.15 K) / Hartree | 0.071228 | 0.087259 |
| Activation Energy (298.15 K) / kcal mol-1 | 44.70 | 54.76 |
| DOI | DOI:10042/to-13775 | DOI:10042/to-13776 |
| Chair TS | Boat TS | |
| Sum of electronic and ZPE (0 K) /Hartree | -234.467847 | -234.402340 |
| Activation Energy (0 K) / Hartree | - | 0.066860 |
| Activation Energy (0 K) / kcal mol-1 | - | 41.96 |
| Sum of electronic and ZPE (298.15 K) /Hartree | -234.468283 | -234.401901 |
| Activation Energy (298.15 K) / Hartree | - | - |
| Activation Energy (298.15 K) / kcal mol-1 | - | - |
| DOI | DOI:10042/to-13756 DOI:10042/to-13791 |
DOI:10042/to-13759 DOI:10042/to-13792 |
Three results that corresponded to the expected values were obtained, and shown in bold. Although the data set produced here is insufficient for solid conclusions to be drawn, the HF/3-21g calculations do indicate the chair TS to be stabler than the boat TS, while the DFT B3LYP/6-31g* results are generally closer to literature values than for the HF-3-21g calculations, due to it being a higher level of theory with a larger basis set.
Diels-Alder Reaction
The Diels-Alder reaction is a [4+2] cycloaddition reaction between a diene and a dienophile, suggested to have an aromatic transition state, which gives either an exo- or endo- product. Their energies can be predicted by computational methods, via comparison of their respective energies. Whether the real major product corresponds to the lower energy conformer will indicate if the reaction is under kinetic or thermodynamic control. Additionally, it is known that second order orbital interactions can contribute to the stability of the transition state, so an analysis of their molecular orbitals is also included in this study.
Cis-butadiene & Ethene
Both cis-butadiene and ethene were optimised using the semi-empirical AM1 method. Both methods gave structures with a C2v symmetry. The HOMO and LUMO of both are shown below:
| HOMO | LUMO | |
|---|---|---|
| MO | 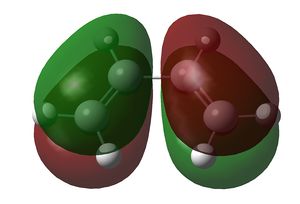 |
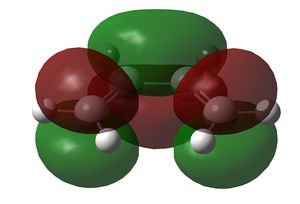 |
| HOMO | LUMO | |
|---|---|---|
| MO | 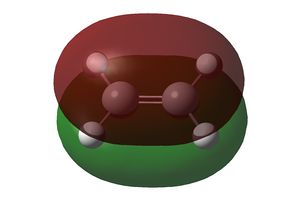 |
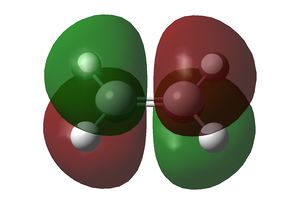 |
The HOMO of cis-butadiene and the LUMO of ethene are asymmetric along the σv plane perpendicular to the molecule, while the LUMO of cis-butadiene and the HOMO of ethene are symmetric about the same plane. Since orbital interactions occur only between pairs of the same symmetry, the Diels-Alder reaction will involve either/both of these pairs of orbitals in these combinations only.
Transition State
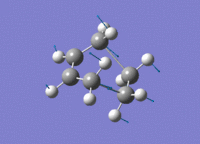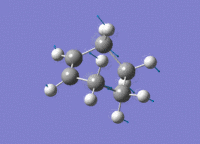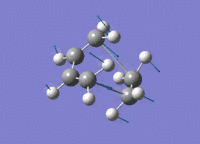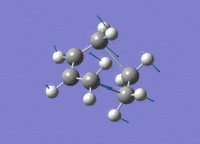
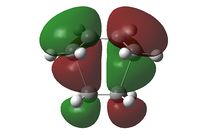
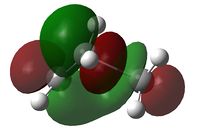
The transition state of the Diels-Alder reaction between cis-butadiene and ethene were optimised with three different levels of theory, with the results tabulated below.
| Imaginary Vibration | HOMO View A | HOMO View B | LUMO View A | LUMO View B |
|---|---|---|---|---|
 |
 |
 |
 |
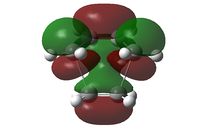 |
The C2v symmetry of the reactants is retained in the transition state. The LUMO is a result of the combination between the LUMO of cis-butadiene and the HOMO of ethene; while the HOMO is due to the combination of the HOMO and cis-butadiene and the LUMO of ethene.
| Imaginary Vibration | HOMO View A | HOMO View B | LUMO View A | LUMO View B |
|---|---|---|---|---|
 |
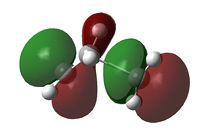 |
 |
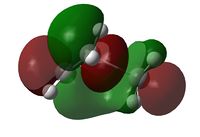 |
 |
| HOMO View A | HOMO View B | LUMO View A | LUMO View B | |
|---|---|---|---|---|
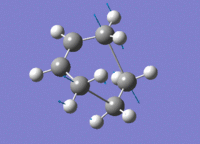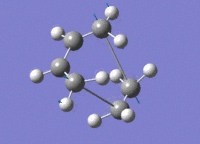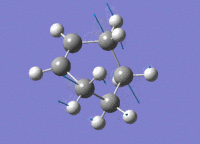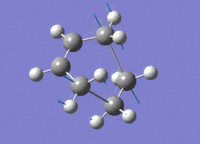 |
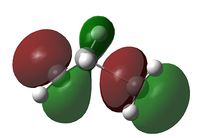 |
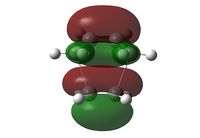 |
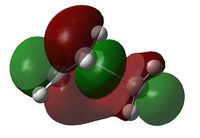 |
 |
While the results obtained through HF/3-21g AND DFT B3LYP/6-31g were largely the same, the AM1 method generated a markedly different HOMO that involves the ethene LUMO and cis-butadiene HOMO. This is an interesting point to note, because while DFT B3LYP/6-31g is technically the higher level of theory to HF/3-21g, their results nevertheless agreed quite well, while contradicting those produced through the AM1 method.
Regioselectivity: Cyclohexadiene & Maleic Anhydride
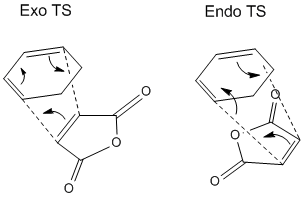
In the previous exercise the reaction between cis-butadiene and ethene can be considered the basic of Diels-Alder reactions. However, the Diels-Alder reaction is much broader than that, and can encompass a range of compounds that behave as the diene and dienophile respectively. A way of demonstrating that is to alter the R substituents, which in addition to altering the electronic energy levels of the HOMOs and LUMOs involved, also introduce second order orbital interactions into the transition state. This exercise investigates the effect of substituents on regioselectivity of the reaction between cyclohexadiene as diene, and maleic anhydride as dienophile.
Reactants
Both cyclohexadiene and maleic anhydride were optimised using DFT B3LYP/631g(d) level of theory prior to any transition state calculations.
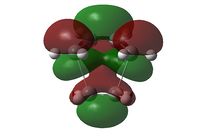
| HOMO | LUMO | |
|---|---|---|
| MO | 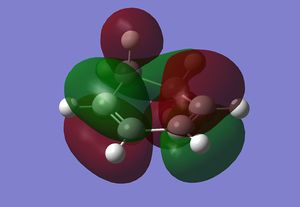 |
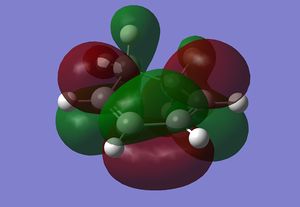 |
| HOMO | LUMO | |
|---|---|---|
| MO | 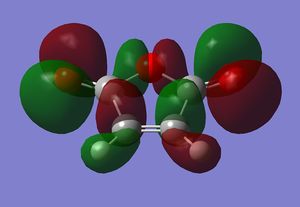 |
 |
Endo Transition State
The Endo transition state was optimised using the Frozen coordinate method, with the DFT B3LYP/631g* level of theory. The C-C bond lengths were set to 2.2 angstroms as with cis-butadiene and ethene. The single imaginary vibration is confirmation of successful optimisation. The bond angles and bond lengths can be viewed from the Jmol file below:
|
|||||
| Imaginary Vibration | HOMO-1 | HOMO | LUMO | LUMO+1 |
|---|---|---|---|---|
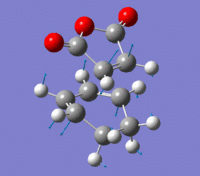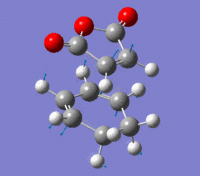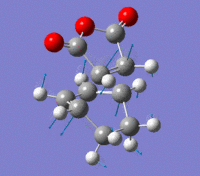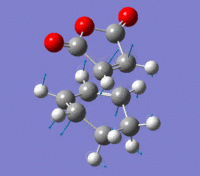 |
 |
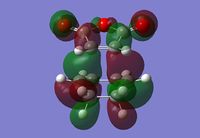 |
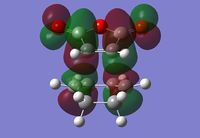 |
 |
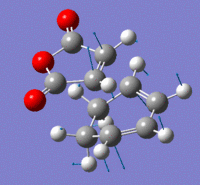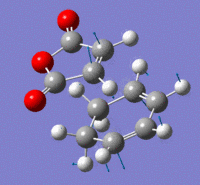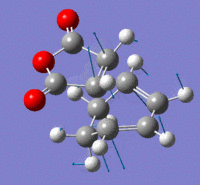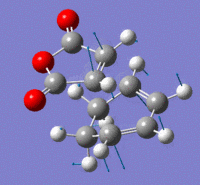
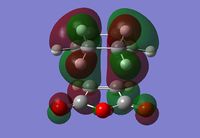
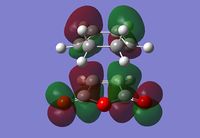
Exo Transition State
The Exo transition state was optimised using the Frozen coordinate method, with the DFT B3LYP/631g* level of theory. The C-C bond lengths were set to 2.2 angstroms as with cis-butadiene and ethene. The single imaginary vibration is confirmation of successful optimisation. The bond angles and bond lengths can be viewed from the Jmol file below:
|
|||||
| Imaginary Vibration | HOMO-1 | HOMO | LUMO | LUMO+1 |
|---|---|---|---|---|
 |
 |
 |
 |
 |
Conclusion
The Cope Rearrangement and Diels-Alder reactions were investigated. The reactant and product conformers of 1,5-hexadiene in the Cope rearrangement were analysed along with the boat and chair transition states, using various methods to arrive at the results with comparison of their different advantages. The chair TS conformation was found to be the stabler one.
The Diels-Alder reactions between cis-butadiene and ethene, and between 1,5-cyclohexadiene and maleic anhydride were both investigated as well. Particular attention was paid to the molecular orbitals relevant to the transition state.
References
All links to D-space are adjacent to the relevant files.
