Rep:Complab3:zeya1989

Module Introduction

In this set of computational experiments, the transition structures will be characterised on potential energy surfaces for the Cope rearrangement and Diels Alder cycloaddition reactions. The transition state structures will be located based on the local shape of a potential energy surface, using orbital-based methods, numerically solving the Schrodinger equation. All calculations in this module were carried out on Gaussian 09W and then visualised in GaussView 3.0 and/or GaussView 5.0, as well as occasional use of ChemBio3D 12.0 Ultra.

General Note on Accuracy and Convention

total energies are reported in atomic unit of Hartree (E_'h').
relative energies are reported in KJ/mol, and are only valid for systems with identical number and type of atoms.
the energy calculate has an error of ≈ 10 kJ/mol, which is equivalent of 0.00381 Hartree(1E_h = 2625.5 kJ/mol)
the dipole moment is accurate to about 2 decimal places, ie 0.01 Debye.
frequencies in wavenumbers are by convention reported to the nearest whole integer with stematic error of around 10%.
intensities are reported with no dedimal places by convention although accuracy is much less than this.
bond distances are accurate to ≈ 0.01 Å
bond angles are accurate to ≈ 0.1°
1 Hartree unit (E_h) = 2625.5 kJ mol^-1 = 627.51 kcal mol^-1

The Cope Rearrangement

The Cope Rearrangement is an example of a [3,3]-sigmatropic shift rearrangement, and is generally accepted that the reaction occurs in a concerted fashion via either a "chair" or a "boat" transition structure, with the "boat" transition structure higher in energy. In this tutorial we will show how Gaussian calculations of enthalpies and activation energies are in good agreement with the experimental values .

Optimising the Reactants and Products

The 10 most stable conformations of 1,5-hexdiene are shown in Appendix 1. It is vital to characterise the conformers since higher energy conformers may stifle the rearrangement. A series of calculations are carried out below to optimise the structures on Gaussian.

a)

The two vinyl groups are manually altered so that they are not on the same side of the C3-C4 bond, reducing their steric repulsion. To make this structure the C2-C3-C4-C5 dihedral angle is set to 180.0°, and then the C3-C4-C5-C6 dihedral angle is set to -109.0 so that the vinyl groups appear to be further apart.

The command for the optimisation is as follows:

%mem=250MB
# opt hf/3-21g geom=connectivity
0 1

Log file: azr07_react_anti.LOG Results summary: azr07_react_anti_rs.txt

After symmetrising the structure a C_i{E,i} symmetry is achieved. Conformer 1 has energy of -231.69254 a.u.

b)

A fresh 'gauche' structure is drawn on Gaussvie with the C1-C2-C3-C4, C2-C3-C4-C5 and C3-C4-C5-C6 dihedral angles set at 60°. The energy of this conformer is expected to be higher than conformer 1 as shown above, since the methylene hydrogens are synperiplanar to the vinyl hydrogens in the gauche form, producign steric strain.

Here is the optimisation command:

%mem=250MB
# opt hf/3-21g geom=connectivity
0 1

Log file: azr07_react_gauche.LOG Results summary: azr07_react_gauche_rs.txt

This gauche form is indeed higher in energy at -231.69153 a.u compared to the previous conformer. Conformer 2 has a C₂ symmetry.

c)

To create the lowest energy conformation, the dihedral angles between the three carbon-carbon bond pairs was altered to be 180° to make all carbon-carbon bonds antiperiplanar.

This structure is subjected to the optimisation:

%mem=250MB
# opt hf/3-21g geom=connectivity
0 1

Log file: azr07_react_anti_b.LOG Results summary: azr07_react_anti_b_rs.txt

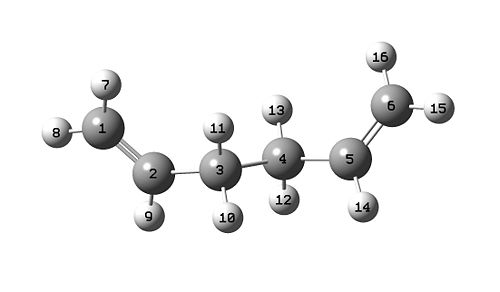
Conformer 3 has energy of -231.69260 a.u and is lower in energy (approx 3 KJ/mol) than conformer 1, it is indeed more stable. The symmetrized structure belongs to the C₂{E,C₂} point group.

d)

From energy and structural comparisons, the above conformers correspond to the labeled equivalents here as follows:

Conformer 1 is equivalent to anti2 with energy at -231.69254 a.u.
Conformer 2 is equivalent to gauche4 with energy at -231.69153 a.u.
Conformer 3 is equivalent to anti1 with energy at -231.69260 a.u.

e)

The anti2 conformation has already been calculated in sectin a). as conformer 1.

f)

Previous minisation of conformer 1 successfully calculated the energy of the structure to a good agreement with that of the anti2 structure. This is then reoptimised using a higher level basis set in order to achieve a better estimate of the conformer.

Conformer 1 is subjected to a DFT-B3LYP/6-31G(d) optimisation:

# opt b3lyp/6-31g(d) geom=connectivity
0 1

Log file: azr07_react_anti_ex.LOG Results summary: azr07_react_anti_ex_rs.txt

Overall the geometry changes are too small to make any visual impact. Table 1 summarises the details of the minor differences in the geometries.

Table 1 - Geometry parameters of Conformer 1
Bond Lengths	HF/3-21G	DFT-B3LYP/6-31G(d)	Dihedral Angles	HF/3-21G	DFT-B3LYP/6-31G(d)
C1-C2 / Å	1.31	1.33	C1-C2-C3-C4 / °	-114.6	-118.6
C2-C3 / Å	1.51	1.50	C2-C3-C4-C5 / °	-180.0	180.0
C3-C4 / Å	1.55	1.55	C3-C4-C5-C6 / °	114.7	118.6
C4-C5 / Å	1.51	1.50
C5-C6 / Å	1.32	1.33

g)

Conformer 1 is subjected to a frequency analysis via the following command:

# freq b3lyp/6-31g(d) geom=connectivity
0 1

Log file: azr07_react_anti_freq.LOG Results summary: azr07_react_anti_freq.txt

No imaginary frequencies are observed; the ananlysis is also fully converged. Below is the data extracted from the Thermochemistry section in the output file:

Sum of electronic and zero-point energies:-234.46920 a.u.
Sum of electronic and thermal energies: -234.46186 a.u.
Sum of electronic and thermal enthalpies: -234.46091 a.u.
Sum of electronic and free energies: -234.50078 a.u.

Optimising the "Chair" and "Boat" Transition Structures

a)

An allyl fragment (CH₂CHCH₂) is drawn in GaussView and optimised using the HF/3-21G method:

# opt hf/3-21g geom=connectivity
0 2

Log file: azr07_allyl_opt.LOG Results summary: azr07_allyl_opt_rs.txt

The optimised allyl fragment is duplicated and the two fragments arranged to approximately 2.2 Å apart to resemble the chair conformation of the transition state.

b)

The chair approximation is subjected to optimisation and frequency analysis to the transition state with the additional keywords opt=noeigen:

# opt=(calcfc,ts,noeigen) freq hf/3-21g geom=connectivity
0 1

Log file: azr07_chair_optfreq.LOG Results summary: azr07_chair_optfreq_rs.txt

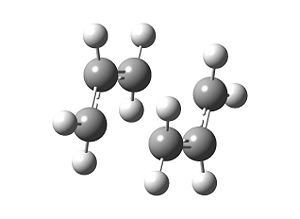
An imaginary frequency at -817 cm^-1 is observed. Further study of the vibrations at this frequency proves that this is where the bond-forming/bond-breaking takes place in the Cope rearrangement:

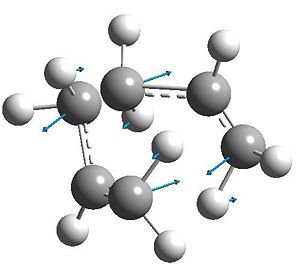
Symmetric vibration at terminal carbons at each fragment, however antiphase within each fragment. This leads to the sigmatropic shift.

c)

Now in order to make sure that the optimisation indeed leads to a transition state minimum rather than a different local minimum, the frozen coordinate method is used by selecting the 'Redundant Coord Editor' option. The terminal carbons from the allyl fragments which form/break a bond during the rearrangement are fixed at 2.2 Å apart, while the rest of the structure will be optimised to an energy minimum.

This is subjected to the following command for optimisation:

# opt=modredundant hf/3-21g geom=connectivity
0 1

Log file: azr07_chair_rce.LOG Results summary: azr07_chair_rce_rs.txt
The optimised structure looks very much similar to the transition state achieved in b), except the bond forming/breaking distances are fixed to 2.2 Å.

d)

Now the transition state will be optimised without calculating the force constants. This requires using a normal guess Hessian modified to include the information about the two coordinates where bond breaking/forming takes place.

The optimisation is subjected to the following:

# opt=(ts,modredundant,noeigen) hf/3-21g geom=connectivity
0 1

Log file: azr07_chair_rce2.LOG Results summary: rce_chair_rce2_rs.txt

The output transition state resembles visually to that produced using the RCE method. To further compare the two structures the numerical differences are studied with regards to structural geometry in Table 2.

Table 2 - Parameter of chair transition state via RCE and Hessian
Parameter	TS (Berny) Optimisation	RCE Optimisation
C-C (allyl,avg.) / Å	1.38	1.38
C-C (trans-allyl,avg.) / Å	2.01	2.02
dihedral angle between tips of chair (abs(avg.)) / °	54.9	54.9
Energy / E_h	-231.61932	-231.61932

As can be seen in Table 2, there are no significant numerical differences with regards to the structures. Both methods are successful in reaching the transition state structure.

e)

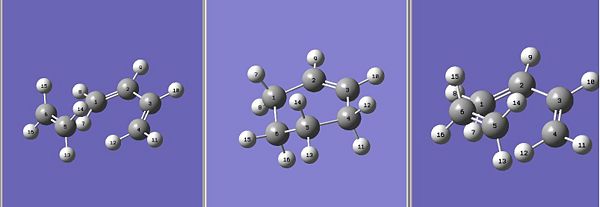
The QST2 method will be used for the boat structure optimisation. This method relies on translating portions of the reactant to yield the product, and stopping at the transition state. The HF/3-21G optimised anti2 structure is duplicated in GaussView, maniputlated and renumbered as shown in Figure 3.

This is then subjected to the following:

# opt=(qst2,noeigen) freq hf/3-21g geom=connectivity
0 1

Log file: azr07_boat_qst_fail.LOG Results summary: azr07_boat_qst_fail_rs.txt
It is not a surprise that the calculation failed as the QST2 method did not rotate about any of the bonds, and thus explains the fact that the output structure looked like a more disassociated version of the chair transition state. To fix this the input structures are modified such that the C2-C3-C4-C5 and C2-C1-C6-C5 dihedral angles, for reactant and product respectively, were 0° (originally 180°) and the C2-C3-C4 and C2-C1-C6, and C3-C4-C5 and C1-C6-C5 bond angles were 100° (originally ~110°), as shown in Figure 4.

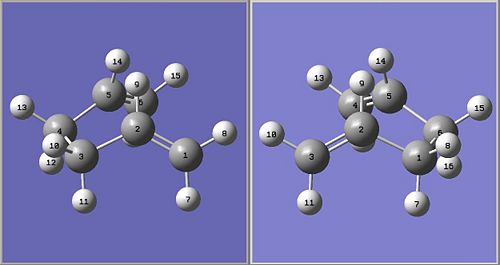
The calculation is run via the following command:

# opt=(qst2,noeigen) freq hf/3-21g geom=connectivity
0 1

Log file: azr07_boat_qst.LOG Results summary: azr07_boat_qst.txt

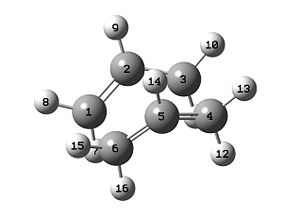
f)

The boat transition state best resembles the gauche3 conformation, while the chair transition state best resembles the gauche2 conformation. To further prove this is indeed the case, an Intricsic Reaction Coordinate calculation is used for each conformer to find the geometric minimum starting from the transition state. It is noted that the initial IRC calculation does not produce a minimum, and there are 3 options to fix this problem. I have decided to use the solution where the IRC is re-run but specifying that the force constants are computed at every step. The advantage of this method is that it is the most reliable.

Firstly the IRC calculation is excuted for the chair transition state, with a 50 step limit and force constants:

# irc=(forward,maxpoints=50,calcall) hf/3-21g geom=connectivity
0 1

Log file: azr07_chair_IRC50fc.LOG Results summary: azr07_chair_IRC50fc_rs.txt

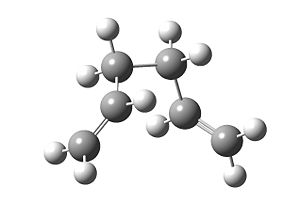
The output corresponds to the gauche2 conformer, both having the same energy too.

Secondly the same process is carried out for the boat transition state, with the following command:

# irc=(forward,maxpoints=60,calcall) hf/3-21g geom=connectivity
0 1

Log file: azr07_boat_IRC60fc.LOG Results summary: azr07_boat_IRC60fc_rs.txt

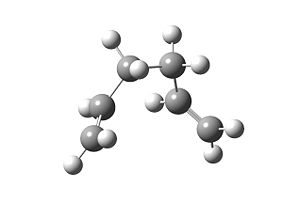
As predicted, the output structure resembles to the gauche3 conformer.

g)

In order to make better comparisons between the activation energy for the Cope rearrangement, it is best to use energies derived from high-level optimisations; thus the chair and boat transition states are firstly optimised again at (DFT-B3LYP/6-31G(d)) level, followed by frequency analysis at the same level in order to produce the Thermochemistry data.

The chair transition state is subjected to the following for optimisation:

# opt=(ts,noeigen,modredundant) b3lyp/6-31g(d) geom=connectivity
0 1

Log file:azr07_chair_reopt.LOG Results summary: azr07_chair_reopt_rs.txt

The frequency analysis for the chair transition state is run via the following command:

# freq b3lyp/6-31g(d) geom=connectivity
0 1

Log file:azr07_chair_refreq.LOG Results summary: azr07_chair_refreq_rs.txt

For the boat transition state the same processes are repeated and the output files are attached as follows:

Reoptimisation log file: azr07_boat_reopt.LOG Reoptimisation results summary: azr07_boat_reopt_rs.txt

Frequency log file: azr07_boat_refreq.LOG Frequency results summary: azr07_boat_refreq_rs.txt

Table 3 and 4 below summarises the data from these calculations.

Table 3 - Energies of transition states and reactant in Hartree
	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.61953	-231.46670	-231.46134	-234.55493	-234.41400	-234.40780
Boat TS	-231.60280	-231.45093	-231.44530	-234.54309	-234.40234	-234.39600
*Reactant (anti2)*	-231.69253	-231.53953	-231.53256	-234.61171	-234.46920	-234.46186

Table 4 - Summary of activation energies (in kcal/mol)
	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.54	44.77	32.65	33.21	33.5 ± 0.5
ΔE (Boat)	55.62	54.66	41.88	41.34	44.7 ± 2.0

From the above data it is straightforward to conclude that it is more favourable if the Cope rearrangement proceeds via the chair transition state, as this conformation has the lower energy and minimal steric strain.

The Diels Alder Cycloaddition

The Diels Alder reaction belongs to a class of reactions known as pericyclic reactions, and are commonly held to be concerted processes. The π orbitals of the dieneophile are used to form new σ bonds with the π orbitals of the diene - this will be proved in this exercise.

The first reaction is the Diels-Alder reaction between ethylene and cis-butadiene.

i)

Cis-butadiene is drawn in GaussView and optimised via the semi-empirical AM1 method:

# opt am1 geom=connectivity
0 1

Log file: azr07_cisbut.LOG

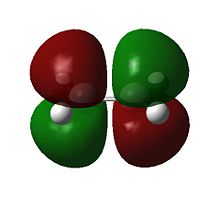
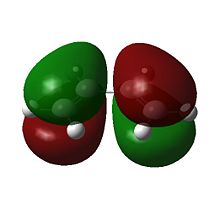
The molecular orbitals are examined so to understand the feasibility of this reaction. It is expected that the HOMO of the diene/dienophile interacting with the LUMO of the dienophile/diene to have the same symmetry. Orbitals can be labeled as either symmetric s or antisymmetric a with respect to the reflection plane, and only orbitals with the same symmetry are able to interact during an reaction. Thus the symmetries of the HOMOs and LUMOs of cis-butadiene and ethene are shown below.

It can be seen that the HOMOs are of different symmetries, as are the LUMOs. Therefore the interaction can only occur across the HOMO/LUMO pair. The HOMO of ethylene and the LUMO of butadiene are both s and the LUMO of ethylene and the HOMO of butadiene are both a. Energetically, the HOMO of the resulting adduct with two new σ bonds is a, indicating a stronger interaction between Ethene HOMO and Cis-butadiene LUMO.

ii)

QST3 method is chosen to determine the transition state for this prototype reaction. Prior to optimisation, three structures are drawn in GaussView, namely cis-butadiene, ethene and the transition state and cyclohexene and arranged spacially as shown in Figure 5 to imply an angled trajectory.

The command code for this QST3 optimisation is as follows:

# opt=(calcall,qst3,noeigen) freq am1 geom=connectivity
0 1

Log file: azr07_ts_guess.LOG

The reaction is a thermal _π4_s + _π2_s cycloaddition, proceeding via a Hückel transition state, and is symmetry allowed.

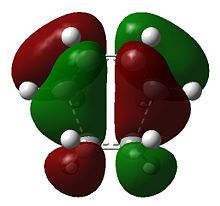
The HOMO is of symmetry a, which as previously shown, is formed by interaction between the HOMO of cis-butadiene and LUMO of ethene.
As on would expect the C(H₂)-C(H) bond lengths are indeed longer than their equivalents in cis-butadiene, being 1.38 Å on average; the C2-C3 bond shows increases in bond order, being a more C=C-reminiscent 1.39 Å (typical C=C bond: 1.34 Å^[1]). The C1-C6 and C4-C5 bond lengths are both 2.11 Å and hence makes the transition state symmetrical, i.e. both bonds are formed simultaneously. The partially formed σ-bonds are less than double the Van der Waals radius(1.9 A for Carbon)^[2].

An imaginary frequency is observed, which correspond to the bond vibration for the partial σ-bonds at -956 cm^-1. The vibration shows the symmetric, concerted formation of the two new σ-bonds. The lowest positive frequency is observed at 147 cm^-1. This vibration is asymmetric and includes a torsional component about the ethene portion.

iii)

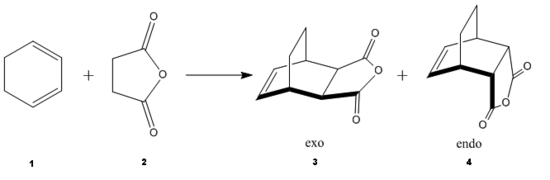
The Diels Alder reaction between cyclohexa-1,3-diene and maleic anhydride is more complicated the previous example, as there are two possible products, the exo 3 and the endo 4 product. The approach of reaction for each isomer is different, and therefore QST3 is employed to determine the transition state for each path.

The reactants and products firstly drawn in ChemBio3D and then imported into GaussView. Each was optimised via the AM1 semi-empirical method.

The exo and endo transition states are both determined via the following command individually:

# opt=(calcall,qst3,noeigen) freq am1 geom=connectivity
0 1

Exo log file: azr07_exo_ts_opt.LOG Endo log file: azr07_endo_ts_opt.LOG

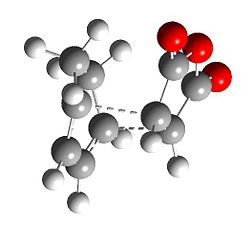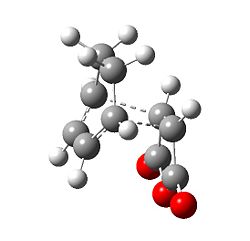The exo isomer has higher energy than the endo isomer, -0.05042 a.u. vs -0.05150 a.u. This is partly due to, structurally, the exo isomer is more strained than than the endo, as it is destabilised more due to repulsion between the anhydride group and the cyclohexadiene ring.

Following the same procedure used in the previous exercise, in order to understand the MOs of the transition states, the MOs of the reactants are firstly examined.

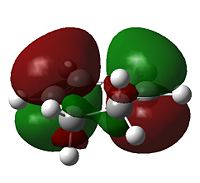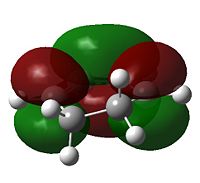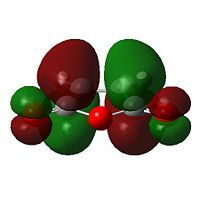The HOMO of cyclohexadiene and LUMO of maleic anydride interacts more strongly than the other pair, because the anhydride group is a strong electron-withdrawing group, and therefore prefers donation from the HOMO of cyclohexadiene into its LUMO. This HOMO/LUMO interaction forms the HOMO of both transition state structures.

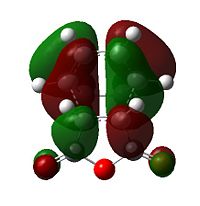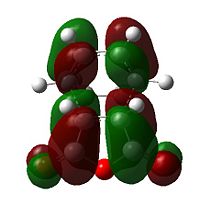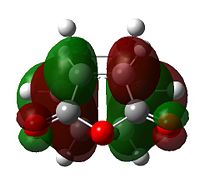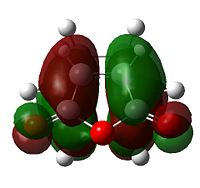Further speculation of the HOMO of the endo isomer reveals the nodal character is such that all the oxygen atoms in the anhydride functionality have nodes in the middle, and lobes both above and below. The central oxygen atom however has lobes extends outward towards the other two oxygen atoms, rather than projecting upwards/downwards as seen in the other oxygen atoms. The same applies to the exo isomer but with smaller blending between the lobes.

The difference in the energy (approx 2.86 KJ/mol) between the two isomers suggests that the endo transition state is the kinetic product since it has lower energy than exo and therefore more stable. In addition to the larger steric strain seen in the exo isomer, the reason for this stabilisation in energy for the endo isomer can be explained by the secondary orbital overlap effect, which is illustrated in Figure 9.

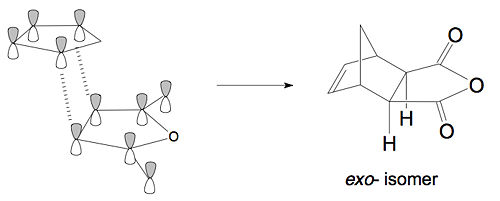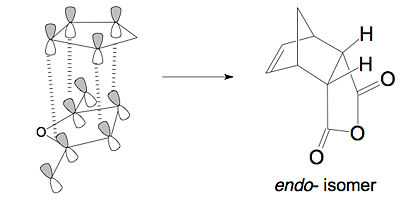The difference implied between the Figure 9 and Figure 8 is that the endo isomer is more stable relative to the exo isomer, because of the additional electron donation from the π-system (HOMO) of cyclohexa-1,3-diene into the orbitals of the electron-poor (LUMO) maleic anhydride, i.e. the middle p-orbitals of the diene with the vacant p-orbitals of the carbonyl groups in the dienophile. This stabilisation is small however it is significant enough to favour the endo isomer over the other on in a kinetically controlled reaction. This secondary orbital overlap, together with the reduced steric repulsion (Figure 6), makes the endo isomer the more favoured transition state. These two factors can sometimes counteract each other, however in this particular case, they act along the same direction, to stablise the endo transition state.

References

↑ J. C. Kotz, P. Treichel, Chemistry & Chemical Reactivity, Volume 2, 2008, 7^th Edition, 387. ISBN 978-0-495-38713-8
↑ R. C. Smoot, R. G. Smith, J. Price, Merrill Chemistry, 1999, 316. ISBN 978-0-028-25527-9

[978-0-495-38713-8-1] J. C. Kotz, P. Treichel, Chemistry & Chemical Reactivity, Volume 2, 2008, 7^th Edition, 387. ISBN 978-0-495-38713-8

[978-0-028-25527-9-2] R. C. Smoot, R. G. Smith, J. Price, Merrill Chemistry, 1999, 316. ISBN 978-0-028-25527-9

[1]

[2]