Rep:Cej15 - The Thermal Expansion of MgO

Abstract

The thermal expansion coefficients of MgO at constant pressure was calculated using computer software GULP. The phonon dispersion curves, density of states and Helmholtz free energy for MgO were obtained at different temperatures. Through lattice dynamic and molecular dynamic simulation methods, the thermal expansion coefficients were calculated to be $3.22\times 10^{-5}$ $K^{-1}$ for molecular dynamics and $2.68\times 10^{-5}$ $K^{-1}$ for lattice dynamics. These were then compared to literature values, $3.11\times 10^{-5}$ $K^{-1}$ and $2.79\times 10^{-5}$ $K^{-1}$ for molecular dynamics and lattice dynamics respectively.

Introduction

System

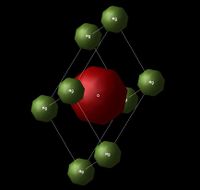
The system used for this experiment was the magnesium oxide (MgO) crystal. Figure 1 and 2 show the lattice structure (FCC - face centered cubic) and the primitive cell of MgO respectively, where the red-coloured atoms correspond to oxygen ions and the green-coloured ones correspond to magnesium ions.

Figure 1: The conventional lattice structure of the MgO crystal.

Figure 2: The primitive cell structure of the MgO crystal.

Lattice Dynamics

The investigation on lattice dynamics is the study of the vibrations of the atoms in the particular lattice. At thermal equilibrium, atoms in a solid do not stay at rest - they vibrate with respect to their equilibrium positions.This is essential as this could lead to the discovery of the substance's heat capacity, free energy, thermal conductivity, phase transitions and many more properties.

The vibration of the atoms, in this case they are called phonons, results in lattice waves propagating through the lattice and each wave has its corresponding wavelength $\lambda$ and frequency $\omega$. As the values of the wavelengths and frequencies are different in each different type of vibration, wavevector $k$ is used and has equation $k=\frac{2\pi }{\lambda }$. $k$ is proportional to $\frac{1}{\lambda }$, so is energy ($E=h\omega =\frac{h\upsilon }{\lambda }$). Therefore, as $k$ increases, so will the energy of the vibration.

Thermal Expansion of a crystal

Thermal expansion of a solid occurs when the volume of the substance increases due to an increase in temperature. The distance between the atoms increase, however, this would not be the case if the interaction between the atoms were harmonic, as the equilibrium bond length would stay the same no matter how much the temperature changes.

The thermal expansion coefficient (TEC) of a solid measures how much the solid expands per degree of temperature. The formula used to calculate the TEC is shown below,

$\alpha (T)=\frac{1}{V(T)}(\frac{\delta V(T)}{\delta T}{)}_P$

where $\alpha$ corresponds to the thermal expansion coefficient. The pressure is held constant and only the temperature changes.

Method

Calculating the phonon modes of MgO

the lattice type used for the following calculations was the primitive unit cell of MgO which had cartesian lattice vectors:

$0.000000$ $2.105970$ $2.105970$

$2.105970$ $0.000000$ $2.105970$

$2.105970$ $2.105970$ $0.000000$

and cell parameters:

$a=2.9783$ $\alpha =60$

$b=2.9783$ $\beta =60$

$c=2.9783$ $\gamma =60$

Binding energy: $-41.07531759eV=-3963.1403kJmo{l}^{-1}$

Phonon Dispersion Curves

A phonon dispersion curve was computed for the primitive lattice cell of MgO, as shown in Figure 3. This was done in order to visualize all possible phonon modes of the crystal along a path in k-space.

Figure 3: Phonon dispersion curve for MgO. Npoints were set to 50.

Figure 4: Phonon dispersion curve found in literature.

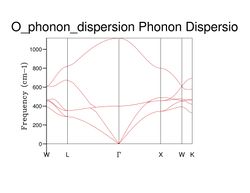
Comparing Figure 3 with Figure 4, it can be seen that the phonon dispersion curve obtained from GULP is very similar to that obtained from the literature.

The phonon density of state (Phonon DOS)

Figure 5: Phonon DOS for grid size 1x1x1.

Figure 6: Phonon DOS for grid size 2x2x2.

Figure 7: Phonon DOS for grid size 3x3x3.

Figure 8: Phonon DOS for grid size 4x4x4.

Figure 9: Phonon DOS for grid size 16x16x16.

Figure 10: Phonon DOS for grid size 32x32x32.

Figure 11: Phonon DOS for grid size 64x64x64.

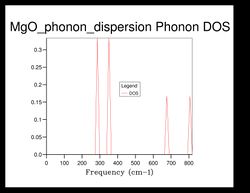
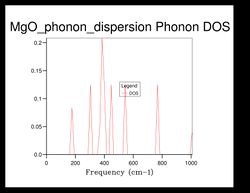
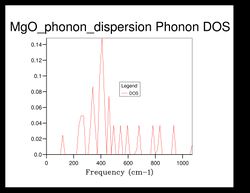
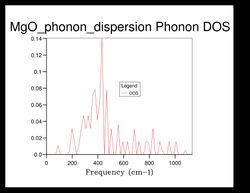
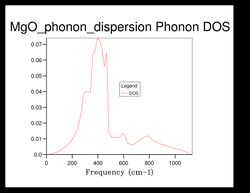
As shown in Figure 5, there are 4 distinct peaks, with 2 that have larger peaks at frequencies $288.49c{m}^{-1}$ and $351.76c{m}^{-1}$ and 2 that have smaller peaks at $676.23c{m}^{-1}$ and $818.82c{m}^{-1}$. The two larger peaks are around twice as large as the smaller ones, indicating that those two peaks have degenerate frequencies. This can be proven by referring back to the phonon dispersion curve obtained previously (see Figure 3). The single k-point sample is at the $L$ position in the dispersion curve. At the lower frequencies at the $L$ position, corresponding to the frequencies $288.49c{m}^{-1}$ and $351.76c{m}^{-1}$, the two curves split into four separate branches, indicating that they are degenerate.

As the grid size increases, the density of states increase as well. For grid size $1\times 1\times 1$, there was only 1 k-point; for $2\times 2\times 2$, there were 4 k-points; for $3\times 3\times 3$ there were 18; for $4\times 4\times 4$ there were 32... It can be seen that after $32\times 32\times 32$ the intensity or frequency of the DOS do not differ much, meaning that grid size $32\times 32\times 32$ would be a reasonable approximation for the phonon DOS. However, the more the grid size is increased, the more reliable the approximation would be.

Comparing the DOS computed at $32\times 32\times 32$ with the much smaller ones, it can be seen that the curve is much smoother and there isn't any discontinuity.

Computing the free energy - the Harmonic Approximation

The lattice type used here was also the primitive unit cell as mentioned above.

Selecting a suitable k-space grid

The temperature used for the following calculations was set at $300K$.

Table 1: variation in free energy with grid size

Grid Size	Free energy / eV	Difference compared to previous grid size / eV
1x1x1	-40.930301
2x2x2	-40.926609	0.003692
3x3x3	-40.926432	0.000177
4x4x4	-40.926450	0.000018
5x5x5	-40.926463	0.000013
6x6x6	-40.926471	0.000008
7x7x7	-40.926475	0.000004
8x8x8	-40.926478	0.000003
9x9x9	-40.926479	0.000001
10x10x10	-40.926480	0.000001
16x16x16	-40.926482	0.000002
32x32x32	-40.926483	0.000001
64x64x64	-40.926483	0.000000

As shown from Table 1, as the grid size increases, the energy differences become smaller until after grid size $32\times 32\times 32$ where there is no more change in energy - the system is stabilized. Therefore, the most suitable k-space grid would be $32\times 32\times 32$.

Thermal Expansion of MgO

The primitive unit cell was used for the following calculations and the structure was optimized at different temperatures and the free energy data was collected at a grid size of $32\times 32\times 32$, as determined from the previous section. The free energy was computed within the quasi-harmonic approximation.

Table 2: variation in free energy and lattice constant with temperature

Temperature / K	Free energy / eV	Lattice constant / A
0	0.172485	2.9783
100	-40.902420	2.9866
200	-40.909377	2.9867
300	-40.928125	2.9876
400	-40.958594	2.9894
500	-40.999436	2.9916
600	-41.049316	2.9941
700	-41.107119	2.9968
800	-41.171892	2.9996
900	-41.243018	3.0026
1000	-41.319849	3.0056

Molecular Dynamics of MgO

The lattice used for the following calculations was a cell that contained 32 units of MgO. The cell volumes at equilibrium were collected at different temperatures. The time step was set to 1.0 femtoseconds, the number of equilibrium steps and production steps to 500, and sampling and trajectory write steps to 5. The volume per formula unit was calculated by dividing the equilibrium cell volume by 32.

Table 3: Variation in cell volume with temperature for molecular dynamics of MgO

Temperature / K	Cell Volume / A^3	Volume per formula unit / A^3
100	599.483366	18.73385519
200	600.580229	18.76813216
300	602.899441	18.84060753
400	604.188880	18.88090250
500	605.758425	18.92995078
600	608.794097	19.02481553
700	610.096648	19.06552025
800	612.495200	19.14047500
900	613.637377	19.17616803
1000	615.970085	19.24906516

Results and Discussion

Thermal Expansion of MgO within quasi-harmonic approximation - Lattice Enthalpy

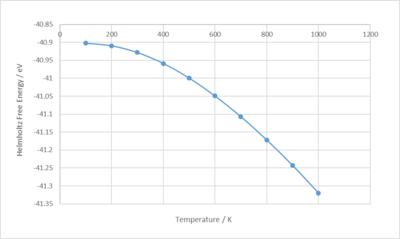
Figure 12 shows a plot of the Helmholtz free energy obtained from the optimisation of the thermal expansion of MgO against temperature. As temperature increases, the energy decreases and the gradient becomes more negative. This shows that the solid is becoming more unstable as temperature increases.

Figure 12: Plot of Helmholtz free energy against temperature.

Below is a plot of the lattice constant against temperature. As temperature increases, so does the lattice constant and tends to increase even more rapidly at higher temperatures. This indicates that the solid is expanding.

Figure 13: Plot of lattice constant against temperature.

Molecular Dynamics of Thermal Expansion of MgO

For this simulation, it did not work at 0K, probably because following classical mechanics, atoms won't have any kinetic energy at 0K and would not move from its equilibrium position, thus not possess motion or any molecular dynamics.

Figure 14: Plot of volume per formula unit against temperature.

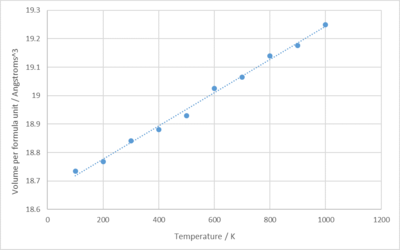
As shown above in figure 14, there is a linear positive relationship between the volume and the temperature.

Comparison between Lattice Dynamics and Molecular Dynamics

Figure 15: Comparison between lattice and molecular dynamics on volume vs temperature.

As shown above, lattice and molecular dynamics differ on thermal expansion. For lattice dynamics, thermal expansion occurs as the equilibrium bond length between the atoms increase due to the anharmonicity of the potential. For molecular dynamics, the solid expands because more energy is put into the system and that increases the kinetic and potential energy of the atoms.

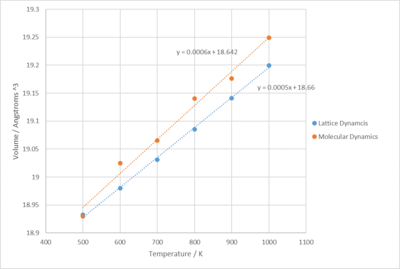
As mentioned previously, the relationship for volume against temperature for molecular dynamic thermal expansion is linear, but for lattice dynamics, the gradient increases in the beginning then turns linear to the end. Therefore, another graph was plotted with only the linear regions of the two graphs, 500K to 1000K, in order to work out the thermal expansion coefficients. The new graph is shown below as figure 16:

Figure 16: Plot of linear region of volume vs temperature.

Conclusion

For this experiment, the thermal expansion coefficients of MgO at constant pressure was calculated using lattice dynamic and molecular dynamic simulation methods. The values of the TECs were obtained according to the equation mentioned in the introduction section. For molecular dynamics, the value calculated was $3.22\times 10^{-5}$ $K^{-1}$ and for lattice dynamics, $2.68\times 10^{-5}$ $K^{-1}$. Comparing these values to those obtained from literature, $3.11\times 10^{-5}$ $K^{-1}$ for molecular dynamics and $2.79\times 10^{-5}$ $K^{-1}$ for lattice dynamics, they are quite similar.