Rep:CMM314

This experiment aims to obtain values for the thermal expansion coefficient of magnesium oxide, MgO, using two approximations; the quasi-harmonic approximation (QHA) and using molecular dynamics (MD). In addition to this, the phonon dispersion and density of states (DOS) are computed at 300K using QHA and analysed, in order to select an appropriate grid size for all consequent calculations using the QHA. This selection is confirmed by analysing the Helmholtz free energy as a function of grid size at 300K. The lattice parameter and Helmholtz free energy are also calculated as a function of temperature using the QHA. The final aim is to compare the two approximations and discuss their limitations.

Introduction

The system

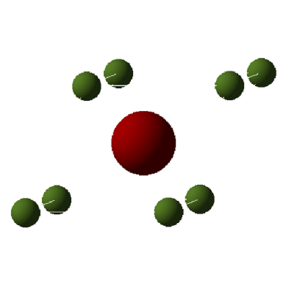
Magnesium oxide, MgO, can be described as a face centred cubic (FCC) ionic lattice with a primitive cell shown in Figure 1 containing one magnesium atom and one oxygen atom. Although the primitive cell contains all the information needed to create the MgO crystal lattice by being periodically repeated infinite times, MgO is more commonly described by its conventional cell, shown in Figure 2, as it demonstrates the FCC structure of MgO more clearly. This is composed of 4 primitive cell units and thus contains 8 atoms. It is a cube with length of each side 4.212 Å, which is known as the lattice parameter.

Figure 1ː Primitive cell of MgO

Figure 2ː Conventional cell of MgO

Methodology

Both approximations were calculated under the Linux operating system. The General Utility Lattice Program (GULP) was employed for the calculations and visualised using DLVisualize. The QHA is based on quantum mechanics; more specifically, the phonons of the crystal. It assumes that the system can be described by a harmonic oscillator. The Helmholtz free energy can be calculated using Equation 1:

$F=E_0+\sum _{k,j}\frac{1}{2}\hslash {\omega }_{j,k}+k_{b}T\sum _{k,j}\ln (1-exp(\frac{-\hslash {\omega }_{j,k}}{k_{b}T}))$

where F=Helmholtz free energy, Eo=internal energy, j=vibrational band, ħ=reduced Plank’s constant, ω=frequency of vibration, T=temperature and kb=Boltzmann’s constant . The second term in the equation refers to the zero point energy. The phonon modes are calculated by adjusting the equilibrium bond displacements to minimise the Helmholtz free energy.

MD is based on classical physics; more specifically, Newton’s second law, which states thatː

$F=ma$

where F=force, m=mass and ɑ=acceleration. This method computes the force on the atoms and consequently acceleration using the equation. It updates initial velocities and positions of the atoms repeatedly until energy and temperature no longer fluctuate, at which point properties can be measured. The timestep chosen for the calculation is 1 femtosecond which is a compromise between efficiency of the calculation and allowing all of the phonons to be sampled reasonably well.

Both methods are used to obtain volume of the cell as a function of temperature. This is required to calculate α, the thermal expansion coefficient, according to Equation 2:

$\alpha =\frac{1}{V_0}(\frac{\partial V}{\partial T})$

where Vo=initial volume, V=volume and T=temperature. The physical origin of thermal expansion is due to the fact that when thermal energy is given to the system, the amplitude of the phonons increases and the atoms vibrate at a longer equilibrium bond distance in order to minimize the free energy of the system. Thus the volume of the crystal lattice increases proportionately to temperature.

Results and Discussion

Quasi-harmonic approximation

Binding Energy

The 'binding energy' of MgO is calculated by summing the total energy of the inter-atomic forces over the infinite lattice, using the primitive cell. This value is -41.0753 eV (4 d.p) per primitive unit cell and represents the amount of energy required to separate the atoms in the lattice to infinite separation.

Phonon Dispersion Curve, Density of states and Free energy for different grid sizes

Figure 3ː Phonon dispersion for MgO

The phonon dispersion curve obtained can be seen in Figure 3. A phonon is a quantum of energy associated with a vibrational wave of a crystal lattice. There are two typesː acoustic and optical phonons, which can be differentiated from each other in the dispersion curve graph due to the fact that acoustic phonons pass through Γ. As there are two atoms in the primitive cell which is three dimensional, we expect six bands on the plot . The dispersion curve is a plot of the frequency against 50 k-points, where k is essentially an index which labels every possible vibration of the crystal. The x-axis features the symmetry points along the conventional path in k-space. A density of states (DOS) produces an average over all k-points and shows the number of phonons at each frequency. A grid size must be chosen for the calculation whereby the denser the grid size, the more k-points are sampled. Calculations to produce a DOS are performed for grid sizesː 1x1x1, 2x2x2, 3x3x3, 4x4x4, 8x8x8, 16x16x16, 32x32x32 and 64x64x64 as can be seen in Figures 4-11. The DOS is related to the dispersion curve, which is best illustrated with the 1x1x1 grid size in Figure 4. There are 4 peaks on the DOS at approximately 290 and 350 cm⁻¹ both with relative intensity 2, and 2 peaks at approximately 680 and 810 cm⁻¹ both with relative intensity 1. From the phonon dispersion curve it can be seen that the 1x1x1 grid DOS graph must refer to the k-point L, as the vertical line x=L shows that 4 bands cross through at the same frequencies as the peaks on the DOS, and the relative intensities on the DOS can be explained by the fact that the two peaks at lower frequencies represent two acoustic bands each which have the same frequencies at symmetry point L.

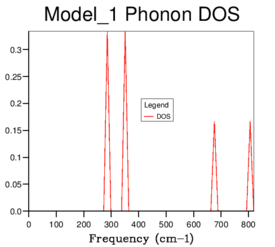Figure 4ː 1x1x1 grid

Figure 5ː 2x2x2 grid

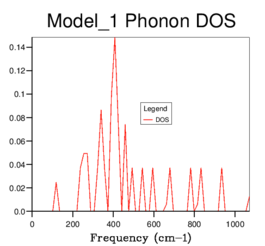Figure 6ː 3x3x3 grid

Figure 7ː 4x4x4 grid

Figure 8ː 8x8x8 grid

Figure 9ː 16x16x16 grid

Figure 10ː 32x32x32 grid

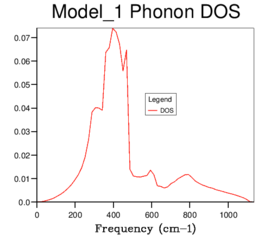Figure 11ː 64x64x64 grid

As grid size is increased, more peaks appear and eventually the graph becomes a smooth curve until no further change is seen, evident by the fact that the 32x32x32 and 64x64x64 DOS graphs are identical. Therefore based on the DOS produced, the 32x32x32 grid size can be used as the minimum size of grid to give a reasonable approximation. Below this, not enough of the features appear in the DOS to be accurate enough for further calculations. The maximum of the 32x32x32 DOS occurs between approximately 380-410 cm⁻¹ and it is in this horizontal region of the phonon dispersion plot that the six bands are most concentrated, further demonstrating that this is a good approximation and how the DOS and phonon dispersion graphs are related to each other.

Table 1ː Helmholtz free energies for increasing grid sizes

Grid size	Free energy (eV)
1x1x1	-40.930301
2x2x2	-40.926609
3x3x3	-40.926432
4x4x4	-40.92645
8x8x8	-40.926478
16x16x16	-40.926482
32x32x32	-40.926483
64x64x64	-40.926483

This optimal grid size would also be optimal for a similar oxide such as CaO. Despite the larger size of a calcium atom than a magnesium atom, both are in the same group and thus have the same charge of +2 in ion form. The lattice parameter for CaO (4.811 Å) is relatively similar to MgO (4.212 Å) and it is also an FCC lattice . This means that their properties in reciprocal space (k-space) will be similar enough to use the same grid size for a good approximation. However the lattice parameter for the Zeolite Faujasite is 24.756 Å and for the metal lithium is 3.509 Å, as well as the latter being a body centered cubic (BCC) lattice . Thus in reciprocal space, the Faujasite unit cell would be much smaller than that of MgO and conversely a lithium unit cell would be larger. Therefore using a smaller grid size than 32x32x32 would be accurate for Faujsaite and a larger grid size would be required for calculations of the same degree of accuracy for a lithium lattice.

In order to confirm that the 32x32x32 grid is a good approximation, the Helmholtz free energy is calculated for each grid size previously used, shown in Table 1. This shows that for accuracy to 1 meV, 2x2x2 can be used and for accuracy to 0.5 meV and 0.1 meV, 3x3x3 can be used. It can be seen that the energy has converged to 6 d.p by time the grid size has reached 32x32x32.

The grid size at which the free energy converges and can therefore be used as a good approximation whilst minimising computational time is expected to be the same for CaO as it is for MgO, smaller for Faujasite and larger for lithium metal for the same reasons as given above.

Lattice parameter and free energy as a function of temperature

Figure12

Figure 13

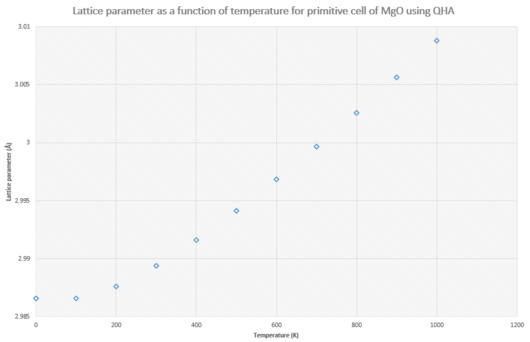Using a 32x32x32 grid size, lattice parameter of the primitive cell and free energy were calculated as a function of temperature, as shown in Figures 12 and 13. Both of these graphs show a quadratic dependence at low temperatures and then follow a positive and negative linear trend respectively. The lattice parameter represents the length of the side of the primitive cell and will thus get larger with increasing temperature as the lattice expands. According to Equation 1 above, the Helmholtz free energy is dependent on vibrational frequency, ω, which is harmonic in nature under the QHA thus explaining the quadratic nature of the free energy graph at low temperature.

Calculation of the thermal expansion coefficient

The thermal expansion coefficient, α, of a lattice is an intrinsic property and can be calculated using Equation 2 in the introduction. Therefore volume is measured as a function of temperature, yielding the graph in Figure 14. There is a quadratic dependence below room temperature, followed by a linear trend. The volumes at 0 and 100K are thus ignored and the gradient for the linear regression line for the rest of the data is obtained to be 0.0005. The initial volume which in this case is the volume at 200K is 18.8562 ų which yields a value for α of 2.65x10^-5K^-1. This is relatively close to and within the same order of magnitude as the literature value of 1.05x10^-5K^-1, measured at 300 K.

Figure 14

Limitations

The main approximation of the QHA is that at high temperatures, the model remains harmonic and thus predicts that the bond will never dissociate, simply continue to vibrate at extreme amplitudes. Therefore as the system approaches the melting point of 3125 K, the model does not take into account the anharmonicity of the phonons and will not reflect reality. Taking an exactly harmonic approximation for a diatomic molecule, the equilibrium bond length would be independent of temperature due to the symmetry of the harmonic potential. This is why the QHA is used; the equilibrium bond length is displaced to minimise free energy of the system. This results in the phonons, and therefore volume, being temperature dependent.

Molecular dynamics

Calculation of the thermal expansion coefficient

The same formula for α, Equation 2, can be used for the MD model. However, a supercell containing 64 atoms, or in other words a 2x2x2 block of conventional MgO cell units, must be used instead of the primitive cell, so the volume measured will be 32 times greater than for that of the primitive cell at each temperature. The reason for this is that if MD was performed on the primitive cell, every cell of the crystal would be moving in phase and this is not a physical representation. Increasing the cell size will increase the accuracy of calculations run using MD, just as increasing the grid size led to higher accuracy when using the QHA. The methods used to determine the minimum grid size able to give accurate calculations for the QHA can be used to demonstrate that the supercell should give the same degree of accuracy with MD, so that the results from the two different approximations can be compared. MD is more expensive and takes longer computational time than QHA and so the same kind of investigation was not performed and a supercell of 64 atoms is assumed to be a good compromise between accuracy and cost. The supercell volume against temperature graph obtained using MD is shown in Figure 15. This follows a positive linear trend and the gradient of the linear regression line is 0.018. The initial volume at 100K is 599.5524 ų which yields a value for α of 3.00x10^-5K^-1 which is very similar to the value obtained using QHA, but slightly further from the literature value than the QHA result.

Figure 15

Limitations

The MD simulation could not be run at 0K as classically the atoms would have no kinetic energy and MD is a classical approach. Another limitation to consider is that the molecular mechanics force fields are inherently approximations.

Comparison of the two approximations

Figure 16ː Comparison of the two approximations for volume calculations at increasing temperatures.

The difference in results between the two approximations can be seen in Figure 16. The QHA is quadratic at low temperatures and then linear, whereas MD is linear for the whole temperature range. The different results can be attributed to the fact that QHA is a quantum approximation and MD is a classical one. QHA has a zero point energy contribution according to Equation 1 and therefore at low temperatures, whilst quantum behaviour dominates, it is a more reasonable approximation. However as the temperature increases and classical behaviour begins to dominate, MD, which does not have any zero point energy contribution, will be a more reasonable approximation. It can also be seen that the results agree with each other much more at higher temperatures which is also explained by the nature of the two approximations. Both of the models will break down above the melting point because in its liquid form, MgO cannot be described by an infinite periodic lattice and therefore the basis of the calculations does not apply.

Conclusion

Table 2

Method	α (10-5K-1)
QHA	2.65
MD	3.00

Two approximations were used to calculate a thermal expansion coefficient for an MgO crystal lattice. These are summarised in Table 2 and show that both methods are able to predict the coefficient to within the same order of magnitude as a literature value measured at 300K, 1.05x10^-5K^-1. The QHA gives a more accurate prediction, and both predictions are an overestimation. It was found that the QHA results in a quadratic dependence at low temperatures and then becomes linear for a variety of properties such as lattice parameter, Helmholtz free energy and cell volume and that MD gives a linear dependence as temperature increases for cell volume due to the fact that they are quantum and classical approximations respectively. Both of the models have important limitations and neither can be used to calculate thermodynamic properties above the melting point of the lattice. Although reasonable grid and cell sizes were used for each method, given more time larger grid or cell sizes could be used to try and improve the accuracy of the calculations.