Rep:BT1215 CP3MD Lab
Introduction
The ability to model reactions using computational simulations is something of great interest, particularly with regard to understanding experimental mechanisms or molecular properties[1]. Modern computational software, such as Gaussian, is able to use a series of quantum mechanical calculations to optimise a reaction system and determine a lowest energy reaction pathway, as well as the predicted energies and structures of any reactants, transition states, and products involved. Within these calculations, there are two important theoretical considerations to take into account:
1. Potential Energy Surface (PES) - The potential energy of a system given as a function of molecular geometry. By changing the molecular geometry (e.g. bond lengths during a reaction), the change in energy and transition state can be computed.
2. Computational Method - Defines the approximations made within the quantum mechanics, balancing accuracy (fewer approximations lead to more precise results) with computational cost (fewer assumptions mean more resource-intensive calculations).
Potential Energy Surface (PES)
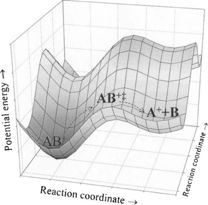
As mentioned before, the PES is a representation of the relationship between the potential energy of a system and its molecular geometry. Given that non-linear molecules have a geometrical freedom of 3N-6 modes (or 3N-5 for linear molecules), where N = the number of atoms in the molecule, the PES therefore has the same dependency, relying on the internal coordinates of the atoms in the system. In order to model a reaction PES, the number of degrees of freedom that are varied is often reduced in order to make the calculation computationally feasible. When plotted graphically, the PES represents a landscape of high and low energy configurations that correspond to turning or stationary points on the surface, with an example plot shown in Figure 1[2]. Low energy turning points correspond to an energetically stable molecular geometry, which are mathematically characterised by having a first derivative equal to 0 (Eq 1), and a positive second derivative (Eq 2), where is potential energy and represents an atomic or reaction coordinate:

The potential energy well surrounding the minimum can be modelled as a Simple Harmonic Oscillator, where the lowest energy point is described by a Taylor expansion. Assuming a harmonic motion modelled by Hooke's law, force constant can be equated to the second derivative in Eq 2. Since the vibrational wavenumber, , is directly proportional to , it can therefore be seen that the molecular configurations corresponding to minimum turning points will only have positive vibrations[4].
The transition state of a reaction corresponds to a saddle point which separates two local minima in the PES, and is essentially a maximum turning point along a particular reaction coordinate of the surface. This can be modelled as a barrier separating two wells, shown in Figure 2[2]. An activation energy is required to overcome this transition state and thus interconvert between the two wells, often denoted reactants and products. The saddle point on the PES surface can be mathematically described as being a local minimum in all directions except for one, where it is equivalent to a maximum turning point. This leads to one reaction coordinate where the second derivative of potential energy is negative. Following the same key discussion above, one negative vibration frequency will be observed in the transition state, while all other frequencies observed will be positive.
It is important to note that, while this discussion of a singular force constant holds true for one-dimentional systems, polyatomic systems require more complicated treatment, since there are multiple force constants and vibrational motions within the system that can actually couple (i.e. one vibration could affect the likelihood of another happening). The general form of these force constants is shown below in Eq 3, where i and j represent degrees of freedom (or coordinates) up to 3N-6:
Software such as Gaussian simplifies these complicated raw motions by first converting the internal coordinates into mass-weighted coordinates to make the coupled force constants equally weighted, before creating a large Hessian matrix of all the coupled force constants. The software then diagonalises the Hessian matrix to give the decoupled, vibrational modes of the molecule[5]. A simplified example of the Hessian matrix that is diagonalised is shown below in Figure 3, where represents the force constants with respect to the mass-weighted coordinates.

Nf710 (talk) 11:35, 16 April 2018 (BST) Excellent understanding of how the force constants are derived. You have clearly done lots of extra reading.
Computational Method
In order to compute the potential energy surface and obtain molecular energies, Gaussian uses quantum mechanical calculations based on the Linear Combination of Atomic Orbitals (LCAO) method. As implied by the existence of the PES, the Born-Oppenheimer approximation is used to separate the electron and nuclear timescales, meaning the nuclei are effectively static on an electron timescale and can be manipulated as such. If this approximation was not true then it would be impossible to calculate the PES, since the electronic energies would constantly be affected by nuclear motion. The LCAO method is essentially a sum of atomic orbitals, , which combine with a weighting coefficient, , to give the overall molecular orbital wavefunction, , shown below in Eqn 4:
The number of atomic orbitals used to build the LCAO is called the Basis Set, which will be discussed further below. The total energy of the molecule is then calculated as a sum of the orbital energies, using the Hamiltonian Operator to solve the Schrödinger equation, where Eqn 5 shows the general form, and Eqn 6 shows the same equation but with the sum of atomic orbitals:
Gaussian represents these equations in matrix form and solves to give the molecular orbital energies, as well as the overall molecule energy. Both the method of calculation and the size of the basis set used to construct the molecular orbital are fundamental factors in determining the accuracy of the computed MOs and energy output, but also in the amount of computational power required. A variety of methods and basis sets can be used to perform optimisations and energy calculations, depending on the computational method chosen. The two methods chosen for all of the following calculations are PM6 and B3LYP (with a 6-31G (d) basis set).
PM6 is a Semi-Empirical method based on the Hartree-Fock method, however it utilises experimental data and/or DFT results (where experimental data is not available) to help speed up the calculation time. Naturally, these assumptions require the system to be modelled by the experimental data used, which may not be an accurate representation. As with the Hartree-Fock method, it also treats electrons as largely independent, and does not account for electron correlation. As a result it represents a rough approximation of the system, although its speed does make it useful for very large systems which would require far too much computational power with a more accurate method. [6]
B3LYP is a hybrid method based on both the Hartree-Fock and Density Functional Theory (DFT) techniques. The Hartree-Fock method is employed in the calculation of the exchange-correlation energy, while DFT is used elsewhere due to its improved efficiency. This is because it only depends on a 3-coordinate system describing the electron, and thus scales 3-dimensionally with the number of basis functions, versus the four-dimensional scaling of the Hartree-Fock method. The smaller scaling results in faster computation, though it is still a lot slower than Semi-Empirical methods. A 6-31G (d) Pople basis set used for the B3LYP calculations, where the numbers represent the basis functions used in the calculation. In general terms, a larger basis set corresponds to a more accurate calculation[4].
To localise the transition state in the reaction systems below, three main methods are possible in Gaussian. The first method is adequate when there is previous knowledge surrounding the reaction mechanism, meaning it is possible to guess the transition state structure and then optimise it. Unfortunately this is very difficult to correctly guess, often missing the transition state. The second method has a higher level of accuracy, and involves optimising the reactants, before setting and freezing the distance between the atoms involved in the reaction. Optimisation to a minima is then performed, followed by a transition state optimisation. This approach provides Gaussian with more information surrounding the reaction pathway, and thus helps guide the optimisation to the correct result. This method was used for Exercise 1.
For Exercises 2, 3, and 4, a third, more complex method was chosen. This involves optimising the product, before breaking the bonds that are formed in the reaction. The distance between the atoms that form these bonds is set and frozen at a specific distance that resembles the transition state. The same calculations as in the second method are then used to identify and optimise the transition state structure. This method is the longest, but is also the most reliable, which was the main reason for its use in more complicated reaction systems.
Nf710 (talk) This section was excellent. Clearly lots of further reading and you backed up your discussions with some equations.
Exercise 1: Diels-Alder Reaction of Butadiene + Ethylene - PM6 Level
(Fv611 (talk) very good job overall, just a little hiccup on the bond length discussion.)
Reaction Overview
Butadiene and ethylene can react to form cyclohexene, shown below in Scheme 1. The reaction occurs via a type of [4+2] cycloaddition, commonly known as a Diels-Alder reaction, through a concerted syn addition[7]. In the case of butadiene and ethylene, since butadiene (the diene) is more electron rich than ethylene (the dienophile), the reaction represents a normal electron demand Diels-Alder cycloaddition.
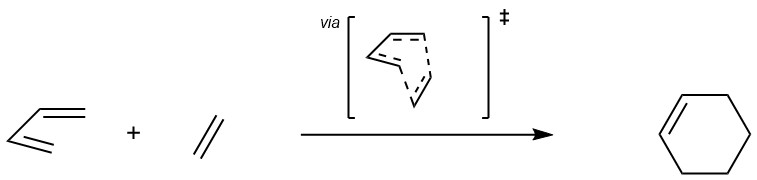
Molecular Orbital Discussion
The frontier molecular orbital (MO) diagram for the reaction between butadiene and ethylene is shown below in Figure 1, and was generated using the calculated Gaussian energies of the transition state and reactants. The transition state and reactants were used in the MO diagram for clarity, since conformational changes and significant orbital mixing in the product make the connection more complicated. As a result, the energies computed for the overlapping MOs are significantly higher than those of the optimised product, especially since the transition state represents a strained conformation. It is also important to note that these energies can only be considered relative to each other due to the inaccuracy of the PM6 optimisation method.
Interactive JMOLs of the two starting materials, as well as the orbitals involved in the bonding interaction can be seen below in Table 1, labelled with both their number, computed energy and occupancy. It is possible to toggle through the generated frontier MOs using the drop down box. Please note that they may not appear to work correctly until after all of the Jmols on the page have loaded.
| Reactant Orbitals | Transition State Orbitals | Product Orbitals | ||||||
|---|---|---|---|---|---|---|---|---|
Orbitals can form stabilising overlap interactions when their associated overlap integral is non-zero. The integral is a quantitative representation of the spatial overlap of the orbitals, and thus an integral equal to 0 is equivalent to no spatial overlap. In order for the overlap integral to be non-zero, the overall integral of the interacting orbital wavefunctions must be a symmetric function. As a result, only orbitals which are both symmetric (S × S = S) or both antisymmetric (AS × AS = S) result in a non-zero overlap integral that allows for a stabilising orbital overlap. Interaction between a symmetric and antisymmetric orbital would lead to an overall antisymmetric function (S × AS = AS) and an integral equal to 0 (representing no interaction). [4] This can also be seen in the MO diagram above, where only orbitals of the same symmetry interact in the Diels-Alder reaction.
Bond Length Discussion
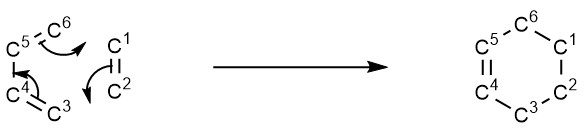
Diels-Alder reactions involve the creation of two new σ-bonds between the diene and dienophile, while three π-bonds are lost and another one is created to complete the cycloaddition. The curly-arrow mechanism for the cycloaddition between butadiene and ethylene is shown below in Figure 5, where each carbon has been numbered so as to allow for the discussion of how each bond length changes throughout the course of the reaction.
The changes in bond lengths with the reaction coordinate are shown below in Graph 1, and were extracted from the PM6 optimised IRC reaction pathway. The typical values for bond lengths between two sp3 hybridised carbon atoms, two sp2 carbon atoms (both single and double bonds), and sp3 and sp2 carbon atoms is shown in Table 2, where all values were obtained from the CRC Handbook of Chemistry and Physics[8]. The calculated bond lengths for the PM6 optimised reactants, products, and transition state can be seen in Table 3. While there are several slightly distinct values for the van der waals radius of a carbon atom, the overall consensus corresponds to a value of 1.70 Å[9].

| Bond Type | Bond Length (Å) |
|---|---|
| C-C (sp3-sp3) | 1.530 |
| C-C (sp2-sp2) | 1.460 |
| C=C (sp2-sp2) | 1.316 |
| C-C (sp3-sp2) | 1.503 |
| Bond Length (Å) | |||
|---|---|---|---|
| Bond | Reactants | Transition State | Products |
| C1-C2 | 1.327 | 1.382 | 1.541 |
| C2-C3 | 3.413* | 2.115 | 1.540 |
| C3-C4 | 1.335 | 1.380 | 1.501 |
| C4-C5 | 1.468 | 1.411 | 1.338 |
| C5-C6 | 1.335 | 1.380 | 1.501 |
| C6-C1 | 3.414* | 2.115 | 1.540 |
(Fv611 (talk) The Van der Waals radius is indeed 1.7A, but for each carbon, meaning the two atoms can be considered to be interacting as soon as their bond length becomes smaller than 2 x 1.7 i.e. 3.4. Incidentally, this is why the "infinite" distance for two carbons is set to be 3.414.)
It is important to note for the reactant values marked with an asterisk that as C2-C3 and C6-C1 are bonds formed during the reaction, the bond length can essentially be assumed as infinite, since there is no interaction between the carbon atoms. The same bonds in the transition state have a length of 2.115 Å, which is significantly larger than the van der waal radius for carbon atoms, suggesting a very weak interaction that still does not have a significant bonding character. In the products these bonds represent C-C (sp3-sp3) bonds, however the optimised value of 1.540 Å shows significant deviation to the typical bond value of 1.530 Å. Comparison with experimentally determined bond lengths of cyclohexene showed reasonable agreement with literature values[10], highlighting the limitation that treating bonds individually from a valence bond theory perspective does not take into account complex orbital interactions that can affect bond length.
C3-C4 and C5-C6 represent the sp2-sp2 double bonds of butadiene in the reactants, while C4-C5 represents the sp2-sp2 single bond connecting them. Their deviation from typical bond length values can be explained by delocalisation through the overlapping p-orbitals, which lengthens the double bonds (due to loss of electron density in the stabilised bonding orbitals) and shortens the single bond (as it gains partial double bond character). Throughout the reaction, the two double bonds lengthen to form sp3-sp2 single bonds, while the single bond shortens to become a sp2-sp2 double bond in cyclohexene.
Finally C1-C2 represents the ethylene sp2-sp2 double bond in the reactants, which again lengthens to form a sp3-sp3 single bond in the cyclohexene product. Once again, the values obtained all agree strongly with literature values for the cyclohexene product[10].
From the bond length data, the transition state appears to have a structure similar to the reactants. Following on from Hammond's postulate, it can be suggested that this reaction must have an early transition state, whereby there is little difference in structure and therefore energy between the reactants and transition state, but a large difference between the transition state and products. This suggestion was confirmed by the IRC calculation, which follows the lowest energy pathway to determine the 1D PES, similar to that seen in Figure 2. The resultant plot, as well as the animated .gif file are shown below in Table 4.
| IRC Plot | IRC .gif File |
|---|---|
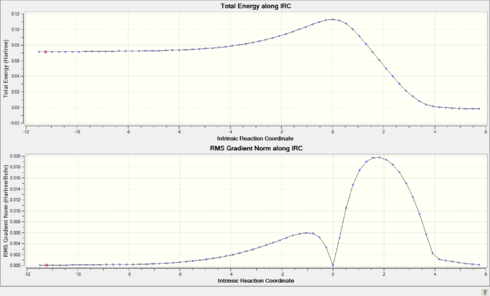
|
|
Transition State Vibration Discussion
As mentioned before, the Diels-Alder reaction between butadiene and ethylene has been experimentally and theoretically proven through various experimental and theoretical studies, however the concerted nature of the pathway can also be formed by looking at the vibration which corresponds to the transition state formation. As can be seen below, the vibration shows the key C1-C6 and C2-C3 bonds forming at the same time, hence identifying a synchronous reaction mechanism.
Output Calculation Files
SM: File:BT1215 CIS BUTADIENE OPT PM6.LOG
IRC: File:BT1215 COMB REACT IRC PM6.LOG
PRETS OPT: File:BT1215 COMB REACT PM6 PRETS OPT.LOG
TS: File:BT1215 BEDIELSALDER ORB COMB REACT TS PM6.LOG
SM: File:BT1215 ETHYLENE OPT PM6.LOG
PROD: File:BT1215 PROD CYCLOHEXENE OPT PM6.LOG
SINGLE POINT ENERGY REACT: File:BT1215 SPE REACT PM6.LOG
Exercise 2: Cyclohexadiene + 1,3-Dioxole - PM6 & B3LYP Level
Reaction Overview
As with Exercise 1, cyclohexadiene and 1,3-dioxole can undergo a [4+2] Diels-Alder cycloaddition reaction, however in this example there are two fundamental points to be aware of. Firstly, by having two disubstituted alkene components, stereoselectivity is introduced whereby the orientation of the alkenes affect the reaction product. The two products formed are denominated endo and exo and are a function of their orientation in the cyclic product. The endo product corresponds to an axially fused ring system (where the extra ring faces downwards), while the exo product represents the equatorial equivalent. For this reaction, the two possible stereoisomers are shown below in Scheme 2.
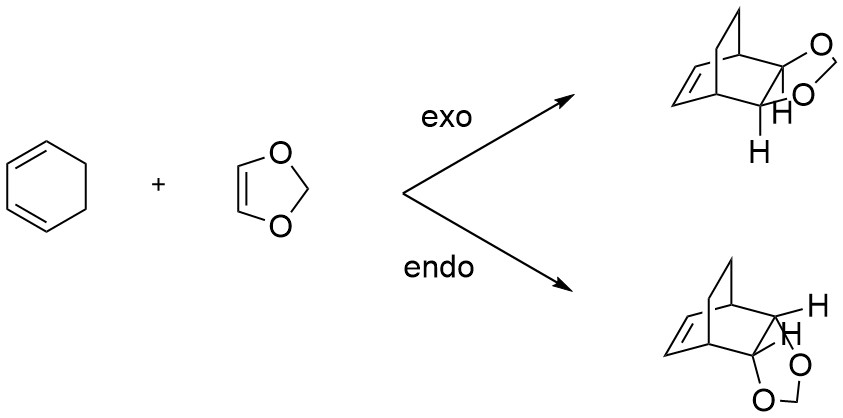
The second key point is that the presence of two electron-donating oxygen atoms adjacent to the dienophile results in an inverse electron demand for the reaction, whereby the electron rich dienophile has a higher energy HOMO and essentially acts as the electron donor. This interacts with the lower energy LUMO of cyclohexadiene to result in an apparent 'reverse' electron flow, and thus generates the HOMO of the transition state. This can be seen qualitatively by comparing the relative reactant MO positions of the normal electron demand reaction above (Figure 4) with those shown below in Figure 6 and Figure 7. The comparative energy gap between HOMO-LUMO overlap interactions in both the normal and inverse demand cases was also compared by looking at the computed orbitals in the optimised PM6 structures, and is shown below in Table 5. As can be seen, the energy gap between the Dienophile HOMO and Diene LUMO is smaller in the Diels-Alder reacton between cyclohexadiene and 1,3-dioxole, leading to the perceived inverse flow. This is confirmed by experimental data with 1,3-dioxole Diels-Alder reactions[11]. The reaction is still thermally allowed following the Woodward-Hoffman rules, since the diene is a (4q+2)s component, and there is no (4r)a component, thus yielding an odd number which corresponds to a thermal reaction[12].
| Diels-Alder Reaction | Diene HOMO-Dienophile LUMO Energy gap / Hartrees | Dienophile HOMO-Diene LUMO Energy gap / Hartrees | Reaction Type |
|---|---|---|---|
| Butadiene + Ethylene (PM6) | 0.39770 | 0.39854 | Normal Electron Demand |
| Cyclohexadiene + 1,3-Dioxole (PM6) | 0.35354 | 0.33984 | Inverse Electron Demand |
It should be noted that the values shown in Table 5 represent the values obtained from single point energy PM6 calculations, since the B3LYP single point energy optimisations of butadiene + ethylene actually suggest an Inverse Electron Demand reaction. This is likely due to the fact that the butadiene + ethylene case is borderline, making it very difficult to distinguish which pathway the reaction undergoes. In addition, there are several different definitions for normal and inverse electron demand, meaning that while the discussion regarding the HOMO-LUMO gap is still important, it does not always accurately predict the electron demand of the reaction.
Unlike in the previous exercise, the reactants, products, and transition states were all optimised with the more accurate B3LYP method (and 6-31G basis set) after an initial PM6 optimisation, giving a more precise comparison of the orbital interactions in the transition state.
Nf710 (talk) 12:10, 16 April 2018 (BST) This is a very good discussion. You should be careful about comparing the different levels of theory however as they have different amounts of electrons contributing the the potential terms.
Molecular Orbital Discussion
(Fv611 (talk) Very good MO diagrams. Well done!)
The MO diagrams for both the endo and exo transition states are shown below in Figure 6 and Figure 7. As with the MO diagram in Exercise 1, the occupied orbitals shown for the transition state are significantly destabilised compared to the expected orbitals in the product, since the transition state represents a significantly constrained and therefore high-energy conformation. While the order of the MO interactions is the same in both cases, the relative stability of the orbitals is significantly different for the endo and exo forms. For the frontier HOMO, the endo equivalent is significantly more stable, which can be explained by the involvement of secondary orbital interactions between the two oxygen p-orbitals and the two p-orbitals of the diene which are not directly involved in the diene-dienophile orbital overlap.
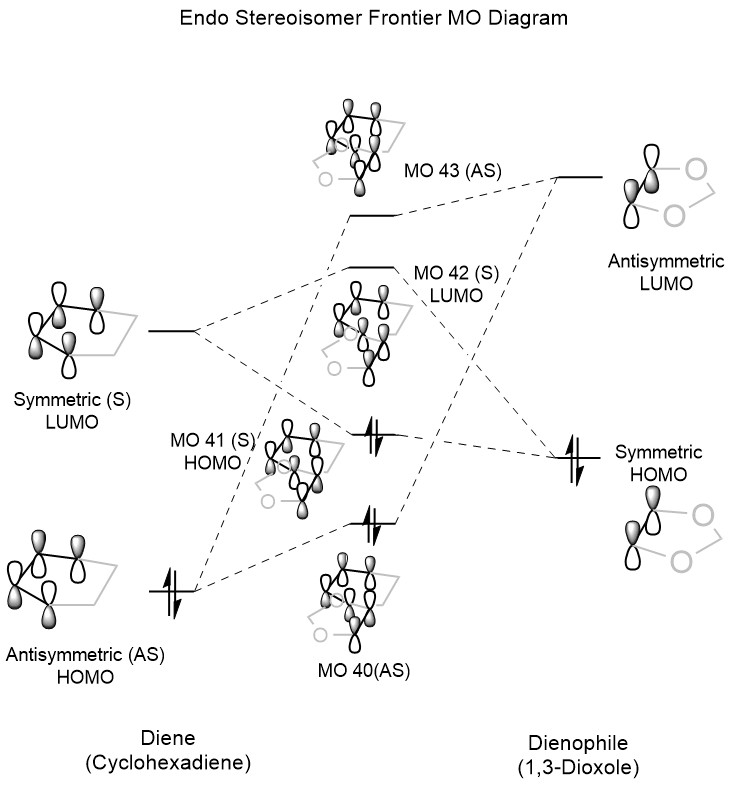
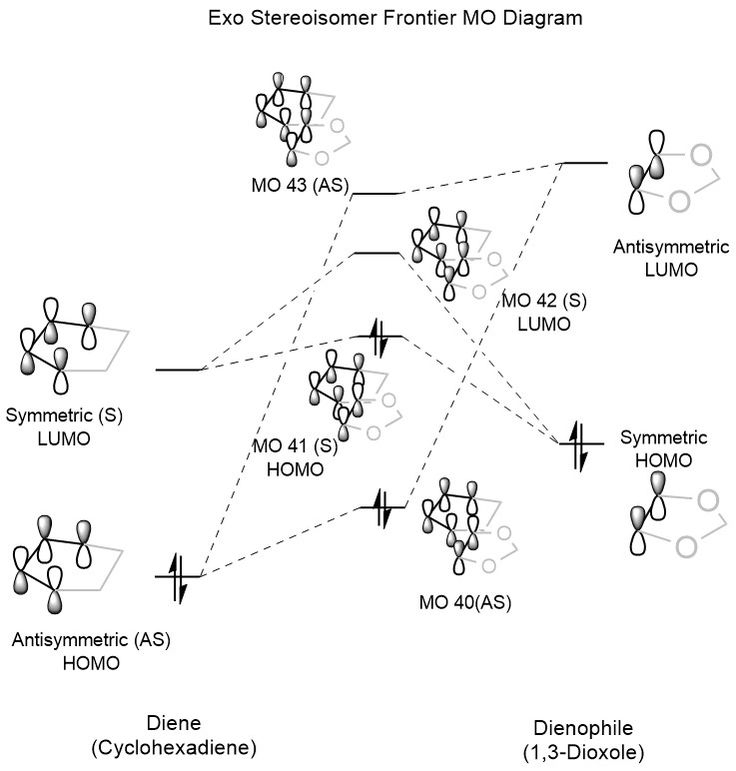
A more thorough discussion of the difference in stabilities is given below in the Energy Discussion section, but secondary orbital interactions can be seen below in the interactive Jmols of the endo orbitals (particularly orbitals 41 and 43). The endo pathway orbitals are shown in Table 6, while those of the exo pathway are given in Table 7. As before, it is possible to toggle through all of the generated frontier MOs using the drop down box.
| ENDO Reactant Orbitals | ENDO Transition State Orbitals | ENDO Product Orbitals | ||||||
|---|---|---|---|---|---|---|---|---|
| EXO Reactant Orbitals | EXO Transition State Orbitals | EXO Product Orbitals | ||||||
|---|---|---|---|---|---|---|---|---|
Energy Discussion
The thermochemical data for the activation and reaction energy of both the endo and exo pathway is given below in Table 8, while the reaction profile is shown below in Figure 8. As can be seen, the endo reaction represents not only the kinetic product for the reaction (by having a lower activation energy) but also the thermodynamic product, as it has a lower energy than the exo form. The reactant, product, and transition state energies are given in Hartrees in Table 9 for comparison. The reactant energies were summed from separate optimisations to ensure there was no interaction between the two that would affect the computed energy.
| Reaction Pathway | Activation Energy / Hartrees | Activation Energy / kJmol-1 (2 d.p.) | Reaction Energy / Hartrees | Reaction Energy / kJmol-1 (2 d.p.) |
|---|---|---|---|---|
| Exo Pathway | 0.063853 | 167.65 | -0.024302 | -63.81 |
| Endo Pathway | 0.060871 | 159.82 | -0.025671 | -67.40 |
| Reaction Pathway | Reactant Energy / Hartrees | Transition State Energy / Hartrees | Product Energy / Hartrees |
|---|---|---|---|
| Exo Pathway | -500.393020 | -500.329167 | -500.417322 |
| Endo Pathway | -500.393020 | -500.332149 | -500.418691 |
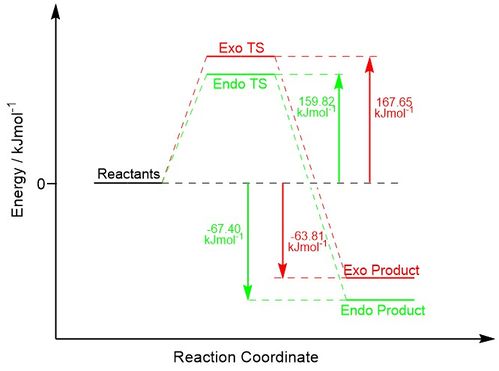
Generally, for alkenes containing substituents that are able to form secondary orbital interactions, the endo product is formed under kinetic control due to a lower energy transition state and therefore a lower activation energy. As mentioned before, these secondary orbital interactions consist of the involvement of the oxygen p-orbitals in the 1,3-dioxole ring which form constructive, symmetry allowed overlaps with the cyclohexadiene frontier orbitals. This increase in overlap leads to a greater stabilisation of the HOMO in the product and transition state, thus also lowering the overall energy of both. These interactions are 'secondary' as their contribution to the bonding is not essential for the reaction to occur, however their impact is significant in determining the stereochemistry of the product. The key secondary orbital interaction between oxygen and cyclohexadiene is shown below in Figure 9, while an interactive Jmol of the endo transition state HOMO with a higher isovalue is shown below to highlight the interaction.
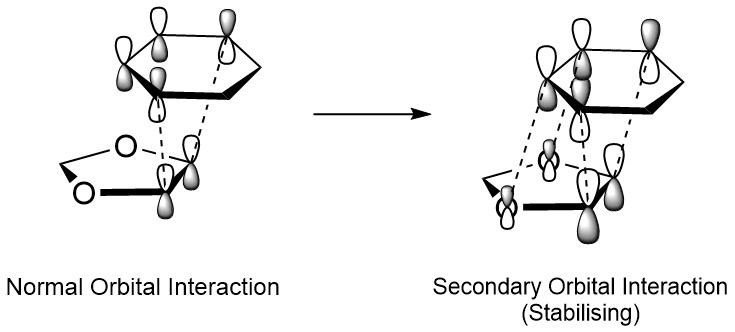
| ENDO TS HOMO Showing Secondary Orbital Interactions | EXO TS HOMO (No Secondary Interaction) | ||||
|---|---|---|---|---|---|
While secondary orbital interactions are important in determining kinetic control, the endo stereosiomer may not be the thermodynamic product if there is a significant steric clash. In this case, the endo form is actually also thermodynamically more stable than the exo form, due to fewer steric interactions between the bridge of the cyclohexene ring and the -CH2 group in the 1,3-dioxole ring. A comparison of the steric interactions is shown below in Figure 10.

Nf710 (talk) 12:21, 16 April 2018 (BST) The sterics diagram has 2 too many Hs. But everything else in this section was done extremely well. Well done.
Output Calculation Files
SM: File:BT1215 CYCLOHEXADIENE OPT PM6.LOG
SM: File:BT1215 CYCLOHEXADIENE OPT B3LYP 2.LOG
SM: File:BT1215 DIOXONE OPT PM6.LOG
SM: File:BT1215 DIOXONE OPT B3LYP.LOG
ENDO IRC: File:BT1215 ENDO OXONE IRC PM6.LOG
ENDO PRETS OPT: File:BT1215 ENDO OXONE PREOPT TS PM6.LOG
ENDO TS: File:BT1215 ENDO OXONE OPT TS B3LYP 2ND.LOG
ENDO PROD: File:BT1215 ENDO OXONE PROD OPT PM6.LOG
ENDO PROD: File:BT1215 ENDO OXONE PROD OPT B3LYP.LOG
ENDO SINGLE POINT ENERGY REACT: File:BT1215 SPE ENDO OXONE SM.LOG
EXO IRC: File:BT1215 EXO OXONE IRC PM6.LOG
EXO PRETS OPT: File:BT1215 EXO OXONE PREOPT TS PM6.LOG
EXO TS: File:BT1215 EXO OXONE OPT TS B3LYP.LOG
EXO PROD: File:BT1215 EXO OXONE PROD OPT PM6.LOG
EXO PROD: File:BT1215 EXO OXONE PROD OPT B3LYP.LOG
EXO SINGLE POINT ENERGY REACT: File:BT1215 EXO OXONE SM OPT PM6.LOG
Exercise 3: Diels-Alder vs Cheletropic Reactions (Xylylene + SO2) - PM6 Level
Reaction Overview
The reaction of xylylene with SO2 is of particular interest, since the involvement of an electron-rich atom such as sulphur, which can easily become hypervalent, allows for new pericyclic reactions. As before, a [4+2] Diels-Alder cycloaddition an occur between the two exocyclic double bonds and the S=O double bond to give two fused six-membered rings with an either endo or exo stereoselectivity. Alternatively, it is possible for the sulphur atom alone to react with the exocyclic diene to give a 5-membered ring fused to the aromatic phenyl ring, in what is called a cheletropic reaction. The reaction with xylylene also introduces an interesting regioselectivity discussion; as well as the cheletropic reaction, a second endocyclic cis-diene is available to react with the SO2 to yield alternative products. This pathway is highly disfavoured compared to the exocyclic Diels-Alder, the reasons of which are explained in the Energy Discussion Section. All of the discussed reaction routes are shown below in Scheme 3

Energy Discussion
As for Exercise 2, the activation and reaction energies for all of the possible routes are given below in Table 10, while a visual representation of the reaction profile can be seen below in Figure 11. For comparison, the reactant, transition state, and product energies are given in Hartrees below in Table 11.
Comparing the activation energies, the endo pathway of the exocyclic Diels-Alder reaction appears to be the kinetic product of the reaction, since it has the lowest energy transition state compared to the reactants. The thermodynamic product for the reaction is clearly the cheletropic product, since it is significantly more stable than any of the Diels-Alder reaction products. This is in agreement with literature results[13], and is likely due to the fact that the cheletropic transition state suffers a higher level of ring strain due to the formation of a 5-membered fused ring, compared to the 6-membered ring formed in the Diels-Alder reactions, which makes the Diels-Alder route kinetically faster. Conversely, the retention of the highly stable S=O bond in the cheletropic product makes this the thermodynamic product. Indeed, as a result of this, the cheletropic product is significantly more accessible experimentally when compared to the reversible Diels-Alder routes. Both the exocyclic Diels-Alder reactions and the cheletropic reaction are all thermodynamically stable compared to the reactants, and can be explained by the formation of the highly stabilised aromatic phenyl ring which lowers the product energy.
In comparison, xylylene is destabilised as it does not possess any aromaticity. The same discussion can be applied to the unfavourable, high-energy endocyclic Diels-Alder reactions; their significantly higher activation barriers and reaction energies compared to the other routes can be explained by the fact there is no aromatic ring in the products, which are also destabilised compared to the reactants due to the creation of a strained bi-fused ring system.
| Reaction Pathway | Activation Energy / Hartrees | Activation Energy / kJmol-1 (2 d.p.) | Reaction Energy / Hartrees | Reaction Energy / kJmol-1 (2 d.p.) |
|---|---|---|---|---|
| Cheletropic | 0.040671 | 106.78 | -0.058385 | -153.29 |
| Exocyclic Exo Diels-Alder | 0.033694 | 88.46 | -0.036928 | -96.95 |
| Exocyclic Endo Diels-Alder | 0.032177 | 84.48 | -0.036685 | -96.32 |
| Endocyclic Exo Diels-Alder | 0.046672 | 122.54 | 0.008922 | 23.42 |
| Endocyclic Endo Diels-Alder | 0.043687 | 114.70 | 0.007226 | 18.97 |
| Reaction Pathway | Reactant Energy / Hartrees | Transition State Energy / Hartrees | Product Energy / Hartrees |
|---|---|---|---|
| Cheletropic | 0.058383 | 0.099054 | -0.000002 |
| Exocyclic Exo Diels-Alder | 0.058383 | 0.092077 | 0.021455 |
| Exocyclic Endo Diels-Alder | 0.058383 | 0.090560 | 0.021698 |
| Endocyclic Exo Diels-Alder | 0.058383 | 0.105055 | 0.067305 |
| Endocyclic Endo Diels-Alder | 0.058383 | 0.102070 | 0.065609 |

The .gif files for the IRC calculations of the reaction routes are shown below. Please note that they may not play smoothly until the interactive Jmols above load. A variety of interesting results can be seen from the animations. All of the Diels-Alder reactions occur via an asynchronous bond formation, where the C-O bond forms before the C-S bond. This could be due to the fact that the smaller, more electron dense oxygen atom can get closer to the xylylene ring to form the C-O bond more quickly than the larger, more diffuse sulphur atom. However, this is merely observational and further calculations would be required to confirm this. In contrast, since only the sulphur atom is involved in the cheletropic reaction, both sigma bonds are formed in a synchronous manner. The IRC plots for all of the reactions are shown below, adjacent to the .gif files. It should be noted that for the Exocyclic Exo route the IRC ran from products to reactants, meaning the reactants are on the right side and the products are on the left side. When compared to the other plots the graph should be reversed.
(Be careful here: you can't use GaussView to decide when precisely a "bond" is formed, as it uses a cutoff distance to decide when to draw a bond Tam10 (talk) 12:15, 4 April 2018 (BST))
| Cheletropic IRC Plot | Cheletropic IRC .gif |
|---|---|
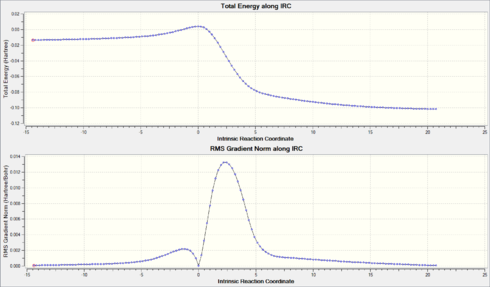
|
|
| Exocyclic Exo IRC Plot | Exocyclic Exo IRC .gif | Exocyclic Endo IRC Plot | Exocyclic Endo IRC .gif |
|---|---|---|---|

|
|

|

|
| Endocyclic Exo IRC Plot | Endocyclic Exo IRC .gif | Endocyclic Endo IRC Plot | Endocyclic Endo IRC .gif |
|---|---|---|---|
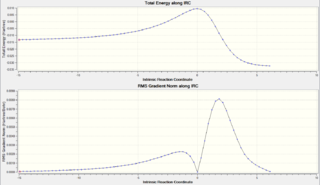
|

|

|
|
Output Calculation Files
SM: File:BT1215 SO2 SM PM6.LOG
SM: File:BT1215 XYLYLENE SM PM6.LOG
CHELO IRC: File:BT1215 CHELO XYLYLENE IRC PM6.LOG
CHELO PRETS OPT: File:BT1215 CHELO XYLYLENE REDUNDANT OPT.LOG
CHELO TS: File:BT1215 CHELO XYLYLENE TS PM6.LOG
CHELO PROD: File:BT1215 CHELO XYLYLENE REOPT PM6.LOG
DA EXOCYCLIC ENDO IRC: File:BT1215 ENDO DIELS-ALDER XYLYLENE IRC PM6.LOG
DA EXOCYCLIC ENDO PRETS: File:BT1215 ENDO DIELS-ALDER XYLYLENE PRETS OPT PM6.LOG
DA EXOCYCLIC ENDO TS: File:BT1215 ENDO DIELS-ALDER XYLYLENE TS PM6.LOG
DA EXOCYCLIC ENDO PROD: File:BT1215 ENDO DIELS-ALDER XYLYLENE OPT.LOG
DA EXOCYCLIC EXO IRC: File:BT1215 DIELS-ALDER XYLYLENE IRC PM6.LOG
DA EXOCYCLIC EXO PRETS: File:BT1215 DIELS-ALDER XYLYLENE REDUNDANT OPT.LOG
DA EXOCYCLIC EXO TS: File:BT1215 DIELS-ALDER XYLYLENE TS PM6.LOG
DA EXOCYCLIC EXO PROD: File:BT1215 DIELS-ALDER XYLYLENE REOPT PM6.LOG
DA ENDOCYCLIC ENDO IRC: File:BT1215 HIGH ENERGY IRC.LOG
DA ENDOCYCLIC ENDO PRETS: File:BT1215 HIGH ENERGY PREOPT TS PM6 2.LOG
DA ENDOCYCLIC ENDO TS: File:BT1215 HIGH ENERGY TS PM6.LOG
DA ENDOCYCLIC ENDO TS: File:BT1215 HIGH ENERGY TS CHECK ORB.LOG
DA ENDOCYCLIC ENDO PROD: File:BT1215 HIGH ENERGY PRODUCT OPT PM6.LOG
DA ENDOCYCLIC EXO IRC: File:BT1215 DA EXO HIGH ENERGY IRC PM6.LOG
DA ENDOCYCLIC EXO PRETS: File:BT1215 DA EXO HIGH ENERGY RED OPT PM6.LOG
DA ENDOCYCLIC EXO TS: File:BT1215 DA EXO HIGH ENERGY TS PM6.LOG
DA ENDOCYCLIC EXO PROD: File:BT1215 DA EXO HIGH ENERGY PROD OPT PM6.LOG
4π Electrocyclic Reactions: [1,1']-bicyclohexene - PM6 Level
Reaction Overview
The Woodward-Hoffman rules are also essential in predicting the stereochemistry of other pericyclic reactions, including electrocyclic reactions which involve the loss of a π bond and the creation of a σ bond that causes the cyclisation of the molecule. The mechanism for this reaction, shown in Scheme 4, is shown below. For this investigation, [1,1']-bicyclohexene was chosen, with a core diene structure analogous to that of butadiene. This electrocyclic reaction is denoted 4π as 4π electrons are involved in the cyclisation.

The stereoselectivity concerns of this reaction are very important, as shown by the Woodward-Hoffman rules[13], since two possible reactions can occur depending on the conditions that the diene is reacting under. [1,1']-bicyclohexene can cyclise under thermal conditions via a conrotatory mechanism, shown below in Figure 12. This is allowed due to the presence of a π4a orbital component which, when 'pulled together', causes the Hydrogen atoms to rotate in the same direction. An alternative possibility is a disrotatory mechanism with a π4s orbital component; this is thermally disallowed, but can occur under photochemical conditions to yield a trans-alkene product.
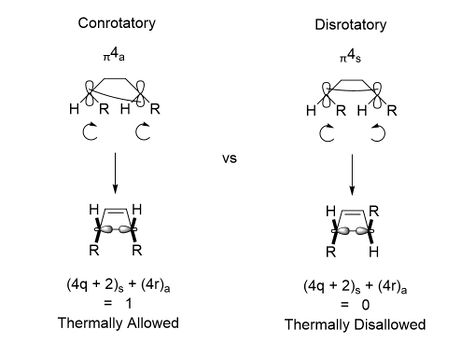
The full explanation as to whether a reaction is thermally allowed or disallowed can be explained by looking at the frontier orbital overlaps in both a conrotatory and disrotatory mechanism. For simplicity, the orbitals of the analogous butadiene will be used, however the explanation can be directly applied to [1,1']-bicyclohexene. In a conrotatory mechanism, the two terminal symmetry orbitals of butadiene (on the top left of the diagram) shown in Figure 12 can be superimposed using a C2 axis perpendicular to the plane of the screen. For a disrotatory mechanism however, the same orbitals are reflected in a σ symmetry plane that is perpendicular to the screen and runs through the centre of the butadiene. It is important to note that while the symmetry based orbitals often used to describe WH rules cannot be directly compared to the frontier molecular orbitals, the symmetry linking both sets of orbitals remains the same here.
The symmetry of the frontier orbitals of butadiene can then be determined based on these two operators, and a correlation diagram composed to identify which orbitals can overlap in the reaction to make the product. The correlation diagrams for the conrotatory and disrotatory mechanisms are shown below in Figure 13. As can be seen, the conrotatory mechanism involves the transfer of electrons from the ground state orbitals of the butadiene into the ground state orbitals of the cyclobutene, resulting in a small energy barrier for the reaction. In contrast, the disrotatory mechanism requires the excitation of electrons into an excited state antibonding orbital, giving it a much larger energy barrier and making the reaction thermally disallowed.
While this provides an elegant way of explaining the WH rules, it must be stated that it cannot provide significant insight into the structure of the product orbital, since the reaction proceeds via a 4n Mobius transition state and this allows all of the orbitals to rotate and switch symmetry. The actual frontier orbitals can be seen below in the MO/Energy Discussion.

(Good intro, and you have labelled your symmetry axis Tam10 (talk) 13:04, 4 April 2018 (BST))
MO/Energy Discussion
In this discussion, the thermally allowed pathway will be focused on due to time limitations that meant that the full calculation of the photochemical route could not be performed. All optimisations were performed at the PM6 level, with the key MOs for the reactant, transition state, and product, given below in Table 12. As can be seen, MO 32 of the product is different to the WH predicted frontier orbital. The expected bonding interaction appears as part of MO 31, along with a more complicated bonding interaction from the alkene of the cyclobutene that appears to be the same symmetry. This is likely a consequence of reacting through a twisted Mobius transition state. It is recommended that further calculations be performed with a more accurate method to confirm the orbital ordering. The rest of the orbitals are as expected in the Reaction Overview section.
| Reactant Orbitals | Transition State Orbitals | Product Orbitals | ||||||
|---|---|---|---|---|---|---|---|---|
The thermochemical data for the reaction is shown below in Table 13, while the energies of the reactant, transition state, and product are given in Table 14. The computed energies reveal that the starting diene is more stable, and therefore the predominant form. This is likely due to the high levels of ring strain in the cyclobutene ring destabilising the product. Kinetically this reaction is also highly unfavourable, with a much higher activation energy than the previous reaction systems discussed. It is possible that the complexity of the cyclohexene rings means a large amount of bond rearrangement is required in order to form the transition state.
| Activation Energy / Hartrees | Activation Energy / kJmol-1 (2 d.p.) | Reaction Energy / Hartrees | Reaction Energy / kJmol-1 (2 d.p.) |
|---|---|---|---|
| 0.104375 | 274.04 | 0.028329 | 74.3777952 |
| Reactant Energy / Hartrees | Transition State Energy / Hartrees | Product Energy / Hartrees |
|---|---|---|
| 0.199543 | 0.303918 | 0.227872 |
An IRC calculation was performed and both the plot and .gif file are shown below. As before, the reaction was computed from products to reactants in the IRC, so the graph should appear reversed. It is also important to note that in the IRC calculation the reactant energy appears to be higher energy than the product, likely due to it converging to a metastable minima where the diene is planar, and not the most stable form of the reactants.
| IRC Plot | IRC .gif File |
|---|---|

|
|
Finally, the imaginary vibration corresponding to the transition state can be seen below. As suggested by the vibration and the IRC, the bond formation in the electrocyclic reaction appears to be synchronous, with the hydrogen atoms rotating in a concerted manner.
Output Calculation Files
SM: File:BT1215 DIENE SM PM6 OPT 2.LOG
IRC: File:BT1215 DIENE IRC PM6.LOG
PRETS OPT: File:BT1215 DIENE TS PREOPT PM6 2.LOG
TS: File:BT1215 DIENE TS OPT PM6 2.LOG
PROD: File:BT1215 PRODUCT ALKENE PM6 OPT.LOG
Conclusion
Computational analysis of 4 different pericyclic systems was performed with a large degree of success, both with the Semi-Empirical PM6 and DFT B3LYP methods. In all cases, it was possible to model and correctly predict experimentally determined reaction mechanisms and transition states. The use of Gaussian was also able to provide insight into the change in bond lengths throughout the reaction, the type of transition state, the electron demand of the reaction, and which routes represent the thermodynamic or kinetic product. The computation of molecular orbitals was crucial in justifying the observed stereoselectivities, providing an elegant visual representation of secondary orbital interactions, as well as other factors affecting product formation. Unfortunately, the complexity of the calculations, along with time constraints, meant that the majority of reaction systems could only be optimised using the PM6 method, and so can only yield qualitative results due to the limitations discussed in the introduction. Conclusions for the individual exercises were as follows:
- Exercise 1 - PM6 - The Diels-Alder reaction of butadiene + ethylene was modelled and shown to occur via a synchronous 4+2 cycloaddition, with a normal electron demand for the reaction. The transition state was correctly identified and confirmed by the presence of a single imaginary vibration frequency, corresponding to product formation, and an IRC calculation was performed to determine an early transition state. This was also confirmed by modelling the change in bond lengths throughout the course of the reaction, showing a transition state structure close to that of the reactants. Despite the inaccuracies of the PM6 method, bond lengths were in reasonable agreement with the literature.
- Exercise 2 - PM6 & B3LYP - The stereoselectivity of the Diels-Alder reaction between cyclohexadiene and 1,3-dioxole was investigated in order to determine whether the endo or exo product represented kinetic and/or thermodynamic control. All structures were optimised first with the PM6 method, before being reoptimised with the B3LYP method in order to give a more accurate depiction of the reaction system and its energies. Relative HOMO-LUMO energy gaps were compared with butadiene + ethylene to determine an inverse electron demand reaction, caused by the electron rich atoms on the dienophile. An MO diagram was constructed, and the kinetic stability of the endo product was explained by the involvement of oxygen p-orbitals in secondary orbital interactions that help to stabilise the transition state. The endo product was also determined to be the thermodynamic product due to the absence of steric clash between the bridged ring and the 1,3-dioxole group.
- Exercise 3 - PM6 - The relative stabilities of five different pericyclic routes for the reaction between Xylylene + SO2 were probed. Optimisations of reactants, products, and transition states were all carried out with the PM6 method. The cheletropic reaction yielded the thermodynamic product via a synchronous bond formation, likely due to the preservation of both S=O bonds. The exocyclic endo Diels-Alder reaction, occurring through asynchronous bond formation, represented kinetic control, due to the fact that the transition state contains a 6-membered fused ring compared to the relatively strained 5-membered cheletropic transition state. An alternative, endocyclic Diels-Alder reaction was investigated and shown to be highly disfavoured due to the fact that no aromatic ring was formed in the product, and the resultant fused ring product had large steric interactions making it thermodynamically unstable compared to the reactants.
- Exercise 4 - PM6 - The thermally allowed, conrotatory 4π electrocyclic reaction of [1,1']-bicylcohexene was investigated, with all optimisations taking place at the PM6 level. The reaction was determined to proceed via a 4n Mobius transition state, which could explain discrepancies between the predicted orbital overlap using orbital symmetry and the observed product orbitals. An IRC calculation was performed and showed a concerted bond formation, while the imaginary transition state frequency observed for the transition state also suggested a concerted, conrotatory mechanism. Due to time constraints, the photochemical disrotatory reaction could not be calculated.
Further work could be explored not only in the computation of the photochemical reaction route in Exercise 4, but also by further modelling more obscure pericyclic reaction routes, similar to computational research performed by W. Grimme et al into cheletropic ene reactions[14]. Alternatively, higher level calculations could be performed to further understand more complex systems, such as ab initio calculations by F. Monnatt et al into the cheletropic and hetero Diels-Alder additions of SO2 to (E)-Methoxybutadiene.[15]
References
- ↑ R. Breslow et. al., Beyond the Molecular Frontier: Challenges for Chemistry and Chemical Engineering, National Research Council, 2003.
- ↑ L. Sleno and D. A. Volmer, J. Mass Spectrom., 2004, 39, 1091–1112.
- ↑ 1 E. G. Lewars, in Computational Chemistry, 2011, vol. 26, pp. 9–43.
- ↑ P. Atkins and J. De Paula, Atkins’ physical chemistry, 2009.
- ↑ A. Ghysels, V. Van Speybroeck, E. Pauwels, S. Catak, B. R. Brooks, D. Van Neck and M. Waroquier, J. Comput. Chem., 2010, 31, 994–1007./
- ↑ J. Řezáč, J. Fanfrlík, D. Salahub and P. Hobza, J. Chem. Theory Comput., 2009, 5, 1749–1760.
- ↑ K. N. Houk, Y. T. Lin and F. K. Brown, J. Am. Chem. Soc., 1986, 108, 554–556.
- ↑ D. R. Lide, CRC Handbook of Chemistry and Physics, 2003, 53, 2616.
- ↑ 1 S. S. Batsanov, Inorg. Mater., 2001, 37, 871–885.
- ↑ V. A. Naumov, V. G. Dashevskii and N. M. Zaripov, J. Struct. Chem., 1971, 11, 736–742.
- ↑ M. A. Mckervey, Alicyclic Chemistry, The Chemical Society, 1978.
- ↑ R. Hoffmann and R. B. Woodward, Acc. Chem. Res., 1968, 1, 17–22.
- ↑ D. Suárez, T. L. Sordo and J. A. Sordo, J. Org. Chem., 1995, 60, 2848–2852.
- ↑ W. Grimme, M. W. Harter, C. A. Sklorz, J. Chem. Soc., Perkin Trans. 2, 1999, 9.
- ↑ F. Monnat, P. Vogel, V. M. Rayón and J. A. Sordo, J. Org. Chem., 2002, 67, 1882–1889.
