Rep:At3815 TS
Introduction
In the following exercises, the reaction pathways of different pericyclic reactions were studied – Diels-Alder and cheletropic. A Diels-Alder reaction is a [4+2] cycloaddition which occurs between a conjugated diene and a substituted alkene, a dienophile to form a substituted cyclohexene system, while for a cheletropic reaction, both new bonds are being made to the same atom on one of the reagents.
The stationary points of the potential energy surfaces (PES) of the reactions were identified and characterised through frequency calculations, and the determination of thermodynamically stability of the different isomers in certain reactions were carried out.
What is meant by a minimum and transition state in the context of a potential energy surface? What is the gradient and the curvature at each of these points?
A PES is a multi-dimensional surface plot which shows the variation of potential energy across two or more reaction coordinates. The potential energy is a function of the independent degrees of freedom of the molecule (for a non-linear molecule: 3N-6 and for a linear: 3N-5, where N = the number of atoms the molecule has), where each of the different degrees of freedom is a normal mode. The normal modes are a linear combination of all the individual translation, rotation and vibration of the molecule and have individual force constants, corresponding to their own normal vibrational modes.
Each vibrational mode has a restoring force as defined by Hooke’s law, which states that:
F = -kx, where F is the restoring force, k the force constant, and x , the displacement of the spring/ bonds from its equilibrium position.
A minimum and transition state on a PES both correspond to a stationary point where the gradient is zero and the first derivative of the Potential Energy vs Bond Distances graph is ∂V(ri)/∂ri = 0. In a reaction pathway, the reactants and products are at minimum points whereas the transition state is the saddle point which is a local maximum on the minimum energy pathway linking the reactants and products.
How would a frequency calculation confirm a structure is at either of these points?
By considering the vibrational frequencies of the different points, minima and transition state can be identified.
In Gaussian, the vibrational frequencies are computed by determining the second derivatives of the energy with respect to the Cartesian nuclear coordinates and then transforming to mass-weighted coordinates. The following equation is used to calculate the force constants between the bonds:

, where k is the molecular force constant and μ, the reduced mass.
As both reactants and products sit in a minimum well, the second derivative of the potential energy function is positive for each degree of freedom as all the coordinates are minimised. As a result, the minima will only have positive and real frequencies and will remain at a minimum unless sufficient energy is provided for them to react. Transition states however, are minimised along all other coordinates except along the reaction coordinate, resulting in a single imaginary frequency.[1]
Nf710 (talk) 22:20, 10 January 2018 (UTC) You shoudl say for the TS all the dimensions are minimums expect one which is a maximum, this is the reaction coordinati
Computational Methods
In this lab, two main optimisation methods were used to calculate the optimised geometry of the transition states. The geometry optimizations proceed as a set of single point energy calculations, where an initial starting geometry calculation is performed. The geometry of the molecule is then varied until the one with lowest energy structure is obtained.
Firstly, a semi-empirical method, PM6 was used where the use of severe approximations and parametrised integrals result in limited accuracy of calculations. However, as this method is fast, it is used for initial optimisation (for exercise 2). Subsequently, a more accurate (but at a much greater computational cost) Density Functional Theory (DFT) optimisation method B3LYP/6-31G(d) was used.
Nf710 (talk) 22:22, 10 January 2018 (UTC) This is a good understanding of PM6, but you could have gone into more detail for B3LYP.
Exercise 1
Reaction Scheme
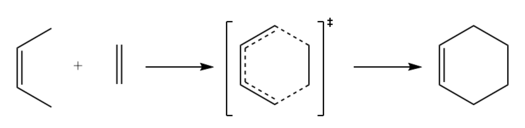
In this reaction, the Diels-Alder cycloaddition of 1,3-butadiene (the diene) and ethylene (the dienophile) to form the product of cyclohexene is studied. This is a π4s + π2s reaction, and is thermally allowed by the Woodward-Hoffman rules[2].
The reactants, transition state and products were optimised at PM6 level. A distance of 2.20 Å was used as a guess for the approximate separation between the terminal carbons of the two reactants (where the bond would form). IRC and frequency calculations were performed on the optimised transition state.
Molecular Orbitals
The molecular orbitals of the reactants, transition states and products are shown in the tables below. The molecular orbitals obtained were then used to construct the MO diagram as shown in Figure 2.
| HOMO | LUMO | |||||
|---|---|---|---|---|---|---|
| 1,3-butadiene | ||||||
| Ethylene |
| MO16 | MO18 (LUMO) | ||||||
| MO17 (HOMO) | MO19 |

(Fv611 (talk) Even though you have calculated the energies of the MOs correctly, you have not adjusted your MO diagram accordingly. Indeed, as this is a TS MO diagram, the LUMO and LUMO+1 of the TS are lower in energy than the LUMO of the dienophile, while the HOMO and HOMO-1 of the TS are higher in energy than both the HOMOs of the reactants.)
What can you conclude about the requirements for symmetry for a reaction?
The symmetry labels 'A' (anti-symmetric) and 'S' (symmetric) correspond to the symmetry of the molecular orbitals (MO) with respect to the mirror plane orthogonal to the sigma bond at the middle of the MO. In order for a reaction to be 'allowed', the overlap between molecular orbitals must result in a non-zero overlap integral, which is satisfied when the symmetry of the molecular orbitals interacting are of the same nature. Therefore, only symmetrical MOs can react with each other, likewise with the anti-symmetrical.
The overlap integral of two orbitals (A and B) is defined as follows:
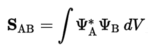
The table belows shows a summary of when a non-zero overlap integral is achieved.
| Interaction | Orbital Overlap Integral |
|---|---|
| Symmetric-Antisymmetric | Zero |
| Symmetric-Symmetric | Non-Zero |
| Antisymmetric-Antisymmetric | Non-Zero |
Bond lengths
| Optimised Structures | Bond distances/ Å | |||
|---|---|---|---|---|
| 1, 3-butadiene | C1-C7 : 1.33519
C7-C9 : 1.46829 C4-C9 : 1.33520 | |||
| Ethylene | C1-C4 : 1.32731 | |||
| Transition State | C1-C7 : 1.37975
C7-C9 : 1.41109 C4-C9 : 1.37982 C1-C11 : 2.11505 C11-C14 : 1.38177 C4-C14 : 2.11442 | |||
| Cyclohexane | C1-C2 : 1.33313
C2-C5 : 1.49269 C5-C8 : 1.53603 C8-C11 : 1.53800 C11-C14 : 1.53602 C14-C1 : 1.49270 |
To make it easier on the eyes, here is a Chemdraw diagram depicting the different labeling for the carbons in the transition state and product:
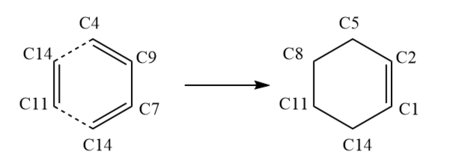
The descriptions on the changes in bond lengths will be based on the labeling in the final product.
It can be observed that all 3 double bonds (C8-C11, C2-C5, C1-C14) elongate from the reactants (1.33 Å in ethylene, 1.34 Å in butadiene) to the transition state (1.38 Å) to the product (1.54 Å).
The distance between C5-C8 and C11-C14 decreases from 2.11 Å to 1.54 Å as the C-C bonds.
The bond length of C1-C2 decreases from 1.47 Å in the reactant to 1.41 Å in the transition state and finally to 1.33 Å in the product.
The typical bond lengths of sp2 and sp3 C-C bond lengths are shown in the table below.
| Bond types | Typical bond length [3] |
|---|---|
| sp2-sp3 | 1.34 Å |
| sp2-sp3 | 1.50 Å |
| sp3-sp3 | 1.54 Å |
For the initial double bonds (sp2-sp3) which change to sp2-sp3 in the transition state and finally sp3-sp3 in the product (or vice versa), the changes in bond lengths is reflective on the changes in hybridisation of the carbons from reactants to transition state to products.
The Van der Waals radius of the C atom[4] is 1.70 Å. In the transition state, as the distance between C5-C8 and C11-C14 is 2.11 Å, it shows that the bonds are forming as the distance is in between the distance of twice the Van der Waals radius and the length of a single C-C bond (1.54 Å).
Vibration of reaction path at transition state
From the Jmol above, the vibrations show that both bonds are being formed simultaneously and at the same rate and hence is synchronous[5].
Exercise 2
Reaction Scheme
The Diels-Alder reaction of cyclohexadiene and 1,3-dioxole to yield its endo and exo products were studied.
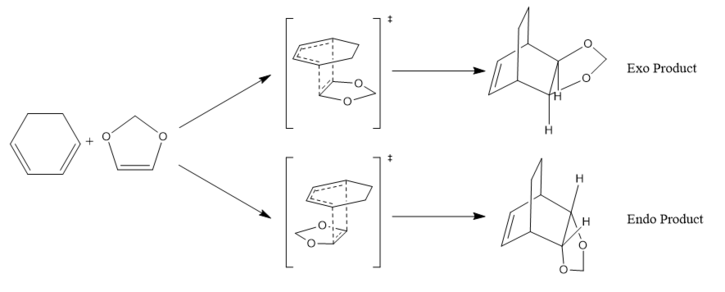
The reactants, transition state and products were initially optimised at PM6 level (as per exercise 1), and then further optimised at the DFT B3LYP level.
| Cyclohexadiene | 1,3-dioxole | ||||
|---|---|---|---|---|---|
Molecular Orbitals
(Fv611 (talk) The MO diagrams are good, and while I appreciate you redoing the schemes of endo and exo orbital interactions, there isn't much point in proposing two equal diagrams if you do not discuss a comparison between the endo and exo case.)
| HOMO | LUMO | |||||
|---|---|---|---|---|---|---|
| Cyclohexadiene | ||||||
| 1,3-dioxole |
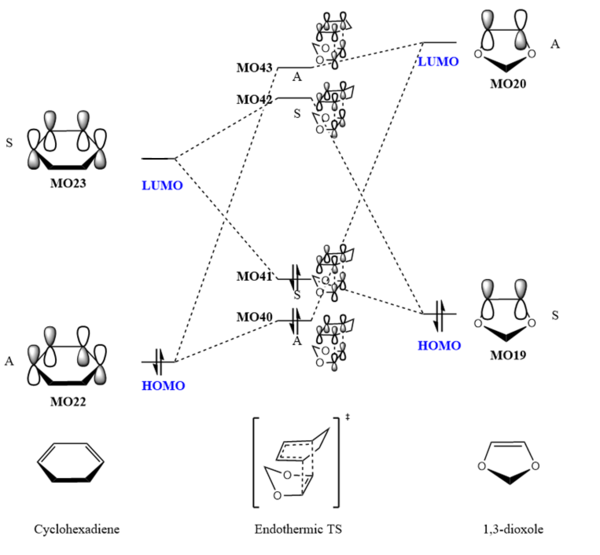
Endothermic Reaction
| MO40 | MO41 (HOMO) | ||||||
| MO42 (LUMO) | MO43 |
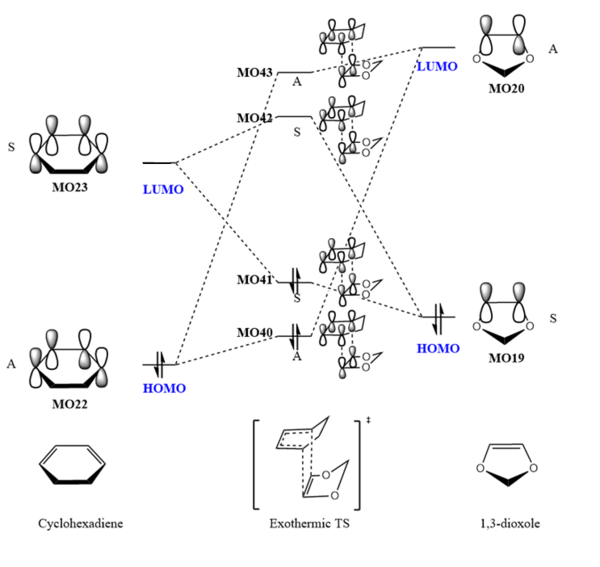
Exothermic Reaction
| MO40 | MO41 (HOMO) | ||||||
| MO42 (LUMO) | MO43 |
Is this a normal or inverse demand DA?
A normal electron demand Diels-Alder reaction, is one between an electron-rich diene and an electron deficient dienophile, and the interaction of the molecular orbitals is between the HOMO of the diene and the LUMO of the dienophile. An inverse electron demand Diels-Alder reaction on the other hand, is a cycloaddition between an electron-rich dienophile and an electron-poor diene.[6]
A diagram of a standard DA reaction is shown in Figure 5 below.
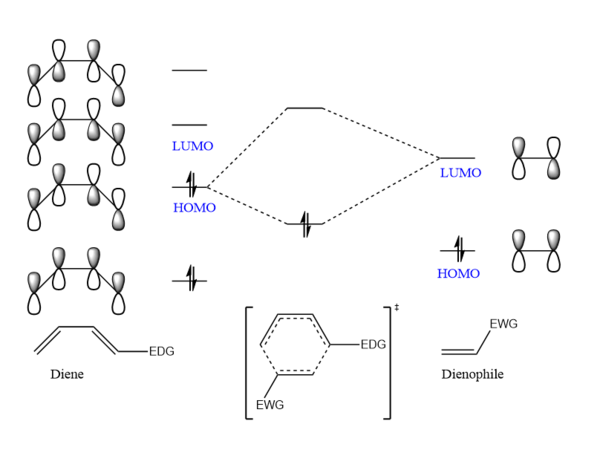
From Figures 3 and 4 however, it can be observed that the reaction has an inverse electron demand as both the HOMO and LUMO of the cyclohexadiene have lower energies than that of 1,3-dioxole. The presence of the oxygen atoms adjacent to C=C in the dienophile makes it more electron rich, resulting in a higher HOMO and LUMO energy. Therefore the energy gap between the LUMO of the diene and HOMO of the dienophile becomes smaller while the HOMO of the diene and LUMO of the dienophile becomes larger. This smaller gap in energy in the former case facilitates a better overlap and therefore gives rise to an inverse demand DA reaction.
Nf710 (talk) 22:29, 10 January 2018 (UTC) This is correct, you could have shown this quantitatively if you would have done a single point calculation on with both reactants in the same window.
Calculations
|
Energy calculation from PM6 (Hatrees/ particle) |
Energy calculation from PM6 (kJmol-1) |
Energy calculation from B3LYP/6-31G(d) (Hatrees/ particle) |
Energy calculated from B3LYP/6-31G(d) (kJmol-1) | |
|
Cyclohexadiene |
0.118063 |
309.9744 |
-233.324375 |
-612593.1466 |
|
1,3-dioxole |
-0.052279 |
-137.259 |
-267.068132 |
-701187.3806 |
|
Sum of reactants |
0.065784 |
172.7159 |
-500.392507 |
-1313780.527 |
|
Endo Transition State |
0.137941 |
362.1641 |
-500.332154 |
-1313622.07 |
|
Endo Product |
0.037804 |
99.2544 |
-500.418691 |
-1313849.273 |
|
Exo Transition State |
0.138904 |
364.6925 |
-500.329163 |
-1313614.217 |
|
Exo Product |
0.037975 |
99.70336 |
-500.417321 |
-1313845.676 |
|
Energies at PM6 level/ kJmol-1 |
Energies at B3LYP/6-31G(d)/ kJmol-1 | |
|
Activation Barrier endo |
189.4482 |
158.457 |
|
Reaction energy endo |
-73.4615 |
-68.746 |
|
Activation Barrier exo |
191.9766 |
166.31 |
|
Reaction energy exo |
-73.01254 |
-65.149 |
Which are the kinetically and thermodynamically favourable products?
The kinetically favoured product is one which requires a lesser activation energy to reach its transition state, while a thermodynamically favoured product is one which has the more exothermic reaction energy. In this case, from Table 2.6 it can be observed that the activation energy to reach the endo product is lower than that of the exo (when comparing values of the same computational method) and the reaction energy of endo is also more exothermic than that of the exo product. Therefore, the endo product is both kinetically and thermodynamically favourable.
Look at the HOMO of the TSs. Are there any secondary orbital interactions or sterics that might affect the reaction barrier energy?
| Endo | Exo | ||||||
|---|---|---|---|---|---|---|---|
|
|
In the endo TS, there are secondary orbital interactions due to the overlap between the non-bonding p orbitals of the oxygen atoms in 1,3-dioxole and the LUMO of cyclohexadiene, which is stabilising and thus lowers the energy of the transition state and in turn, lowers the reaction barrier. For the exo TS, there are no significant secondary orbital interactions and thus does not experience any stabilisation. Since only the endo TS is stabilised, it forms the more kinetically favourable product due to a lower activation barrier.
For both endo and exo products, there are unfavourable steric interactions observed, however it appears to be less significant in the endo product as its’ energy lies lower than that of the exo. This results in the endo product being the thermodynamically favoured product as well.
Nf710 (talk) 22:35, 10 January 2018 (UTC) This was a very good section well done. You have come to the correct conclusions and your energies are correct. You could have shown the SSO and sterics with a diagram to aid in your discussion;
PM6 log files
| Compound | File |
|---|---|
| Cyclohexadiene | File:AT3815PM6MIN2CYCLOHEXADIENE.LOG |
| 1,3-dioxole | File:AT3815PM6MINDIOXOLE.LOG |
| Endo TS | File:AT3815OPTPM6ENDO3.LOG |
| Endo Product | File:AT3815MINENDOPDTEX2.LOG |
| Endo IRC | File:AT3815PM6IRCENDOTS.LOG |
| Exo TS | File:AT3815OPTPM6EXO.LOG |
| Exo Product | File:AT3815MINEXOPDTEX2.LOG |
| Exo IRC | File:AT3815PM6IRC2EXOTS.LOG |
Exercise 3
Reaction Scheme
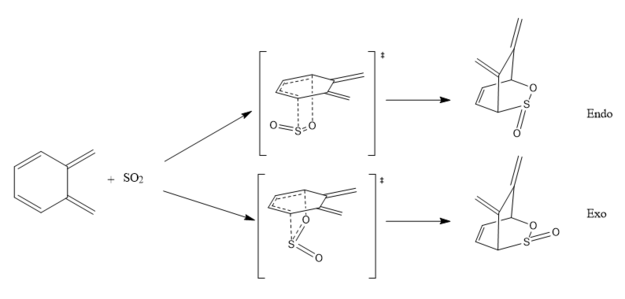
The cycloaddition of xylylene and sulfur dioxide can lead to two different reactions, a Diels-Alder or cheletropic reaction. In this exercise, the different transition states and products of the reactions are studied.
The Diels-Alder reaction can lead to an endothermic or exothermic product as shown in Figure 3.1.
(exo and endo are not abbreviations of exothermic and endothermic Tam10 (talk) 14:40, 3 January 2018 (UTC))
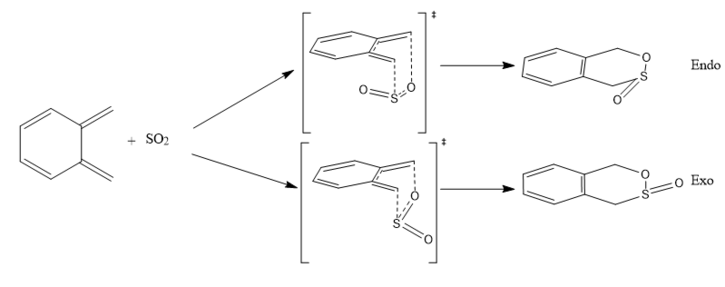
The cheletropic reaction is as shown in Figure 3.2.
Optimised Structures
The reactants, transition states and products were optimised using PM6. The Jmols of the optimised structures are as per below.
| Xylvylene | Sulfur Dioxide | ||||
|---|---|---|---|---|---|
| Optimised structure | Diels-Alder (endo) | Diels-Alder (exo) | Cheletropic Reaction | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Transition State | |||||||||
| Product |
IRC calculation and pathway
| Reaction | IRC Pathway |
|---|---|
| Diels-Alder (Endo) |  |
| Diels-Alder (Exo) |  |
| Cheletropic Reaction |  |
Xylylene is highly unstable. Look at the IRCs for the reactions - what happens to the bonding of the 6-membered ring during the course of the reaction?
From the IRCs above, it can be observed that the 6-membered ring becomes aromatic, resulting in a stable product being formed. The C-C bond lengths in the product are equal with a value of 1.40 Å,suggesting delocalisation of the 6 π electrons over the planar ring system. From the thermochemistry analysis above, it can also be seen that all 3 reactions are highly exothermic, thus the stability of the product is the driving force of the reactions.
Calculations
|
Energy calculation (Hatrees/ particle) |
Energy calculation (kJmol-1) | |
|
Xylylene |
0.178447 |
468.5125985 |
|
Sulfur dioxide |
-0.118614 |
-311.421057 |
|
Sum of reactants |
0.059833 |
157.0915415 |
|
Endo Transition State |
0.091344 |
239.8237 |
|
Endo Product |
0.021699 |
56.97072 |
|
Exo Transition State |
0.092467 |
242.7721 |
|
Exo Product |
0.021452 |
56.32223 |
|
Chelotropic Transition State |
0.099060 |
260.08203 |
|
Chelotropic Product |
-0.000002 |
-0.00525 |
|
Endo |
Exo |
Chelatropic | |
|
Activation Barrier/ kJmol-1 |
82.732159
|
85.680559
|
102.990489
|
|
Reaction energy/ kJmol-1 |
-100.120822
|
-100.769312
|
-157.096792
|
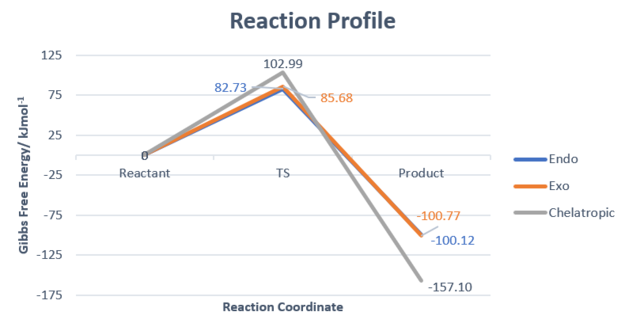
Between the two DA reactions, it can be deduced that the endothermic product would be kinetically favourable due to a lower activation barrier while the exothermic would be more thermodynamically favourable due to a more exothermic reaction pathway.
However considering all 3 reactions, the chelatropic reaction is the most exothermic one, and thus would form the most thermodynamically favourable product. This is due to the presence of the larger sulfur atom relative to a carbon, resulting in the formation of a 5-membered ring product being more stable to that of a 6-membered ring.[7]
(A bit more text would be good for this section. Be careful with spelling. "cheletropic" is usually the accepted version Tam10 (talk) 14:40, 3 January 2018 (UTC))
Extension
Reaction Scheme
As there is a second cis-butadiene fragment in o-xylylene, it can undergo a different Diels-Alder reaction to that in Exercise 3. In this section, the investigation of the endo and exo reactions and their energy profiles are carried out.
Optimised Structures
As per in Exercise 3, the transition states and products were optimised using PM6 method.
(Please note that the file names for the exo are named endo, and vice versa)
| Optimised structure | Diels-Alder (exo) | Diels-Alder (endo) | ||||
|---|---|---|---|---|---|---|
| Transition State | ||||||
| Product |
Calculations
|
Energy calculation (Hatrees/ particle) |
Energy calculation (kJmol-1) | |
|
Xylylene |
0.178447 |
468.5125985 |
|
Sulfur dioxide |
-0.118614 |
-311.421057 |
|
Sum of reactants |
0.059833 |
157.0915415 |
|
Endo Transition State |
0.102070
|
267.984785
|
|
Endo Product |
0.065610
|
172.259055
|
|
Exo Transition State |
0.105055
|
275.8219025
|
|
Exo Product |
0.067304
|
176.706652
|
|
Endo |
Exo | |
|
Activation Barrier/ kJmol-1 |
110.893244
|
118.730361
|
|
Reaction energy/ kJmol-1 |
15.167514
|
19.615111
|
From the calculations made above, it can be seen that the endo and exo Diels-Alder reactions are very thermodynamically and kinetically unfavourable at this second cis-butadiene fragment.
Firstly, it can be seen that the reaction barrier is larger than that of the previous reaction, causing the reaction to occur much slower, if at all - thus it is kinetically unfavorable. Furthermore, the reaction energies for these reaction are positive, indicating endothermic reaction. This indicates that there isn't a thermodynamic driving force for the reactions to take place, which shows that it the reaction is thermodynamically unfavorable.
Conclusion
In this lab, different Diels-Alder reaction pathways were studied through the use of optimisation and frequency calculations. There are various factors which can impact the transition state structure and product of a reaction, such as the manner in which reactants approach one another where steric hindrances and secondary orbital interactions can contribute to the energies of the reaction. This in turn would affect the predicted outcome of a reaction.
From these exercises, it can be seen that the endo reaction barrier is usually lower than that of the exo due to stabilising secondary orbital. The exo product is usually the more thermodynamically favorable one[8], however from Exercise 2, it is seen that the endo product is also the thermodynamically favorable product due to steric factors.
The PM6 level is also found to be insufficient for quantitative analysis of the experiments due to the approximations used in its calculations (but less frustrating to perform due to time taken).
References
- ↑ E. Wigner. T H E Transition State Method . Transit. State Method 1937, 29–41.
- ↑ R. Hoffmann. A claim on the development of the frontier orbital explanation of electrocyclic reactions. Angew. Chemie - Int. Ed. 2004, 43 (48), 6586–6590.
- ↑ E.M. Popov, G.A. Kogan, V.N. Zheltova. Carbon Bond Length. Relationships between lengths, orders, Hybrid. force constants carbon-nitrogen carbon-oxygen Bond. 1970, 6 (1), 14–22.
- ↑ S.S. Batsanov. Van der Waals Radii of Elements. Inorg. Mater. Transl. from Neorg. Mater. Orig. Russ. Text 2001, 37 (9), 871–885.
- ↑ L.R. Domingo, J.A. Sáez. Understanding the mechanism of polar Diels–Alder reactions. Org. Biomol. Chem. 2009, 7 (17), 3576.
- ↑ K.C. Nicolaou, S.A. Snyder, T. Montagnon, G. Vassilikogiannakis. The Diels-Alder reaction in total synthesis. Angew. Chemie - Int. Ed. 2002, 41 (10), 1668–1698.
- ↑ D. Suárez, T.L. Sordo, J.A. Sordo. A Comparative Analysis of the Mechanisms of Cheletropic and Diels-Alder Reactions of 1,3-Dienes with Sulfur Dioxide: Kinetic and Thermodynamic Controls. J. Org. Chem. 1995, 60 (9), 2848–2852.
- ↑ J.H. Cooley, R.V. Williams. endo- and exo-Stereochemistry in the Diels-Alder Reaction: Kinetic versus Thermodynamic Control. J. Chem. Educ. 1997, 74 (5), 582.
