Rep:Ac4515 TS
Introduction
Potential energy surfaces: Transition states and minima
The concept of potential energy surfaces (PES) is key in computational chemistry. A PES is a graphical or mathematical illustration of the relationship between the energy of a molecule, or group of molecules, and its respective geometric coordinates. As the PES is dependent on the geometry of the molecule, and non-linear molecules have 3N-6 degrees of freedom, the PES will have 3N-6 dimensions for non-linear systems. The PES will have many minima, each with corresponding energies and all are stationary points which satisfy: for all geometric coordinates of q and for all q (in all directions)[1]. However, where the distinction comes in between minima and a transition state (or saddle point) is that along the reaction coordinate the transition state is a maximum and satisfies : . Furthermore, a transition state would only have a single negative force constant on the PES, while contrastingly a minimum wouldn't have any. Therefore a transition state structure is confirmed by Gaussian when a particular structure is found to have a single negative vibrational mode. This is a mathematical explanation to distinguish between transition states and minima, below is a diagram to represent this as well[1].
Nf710 (talk) 21:38, 21 February 2018 (UTC) You can diagonalise the hessian at the TS geom and the eigen values will be the curvature of the normal modes (dimensions)

Computational methods used in Gaussian: PM6 and B3LYP
Two different computational methods were employed during this task, the semi-empirical method PM6 and the density dunctional theory (DFT) method B3LYP. Mainly PM6 was used to due to time constraints, but on exercise 2 both methods were used in tandem to yield a higher accuracy.
Firstly, the PM6 is the quicker and less expensive of the two methods but does, however, predict structures with far less accuracy and reliability. A PM6 optimisation uses a Hartree-Fock calculation to obtain the Hamiltonian for the Schrödinger equation. Where the method makes approximations for the Hamiltonian is when terms are approximated using experimental data [2]. These empirical approximations is what makes the method sometimes unreliable and inaccurate.
The second method, B3LYP, is thought of as a hybrid function as it uses two mathematical theories to calculate the Hamiltonian. It uses DFT to calculate all terms in the Hamiltonian apart from the exchange-correlation where it brings in Hartree-Fock theorem [3]. This more thorough method for solving the Hamiltonian makes the method more expensive but does, however, gain results with increased accuracy when compared to PM6.
Nf710 (talk) 21:56, 21 February 2018 (UTC) Good understanding here. Some equations would have been nice to complement the discussion
Exercise 1
(Fv611 (talk) Very good job across the whole section. Well done!)
Reaction scheme
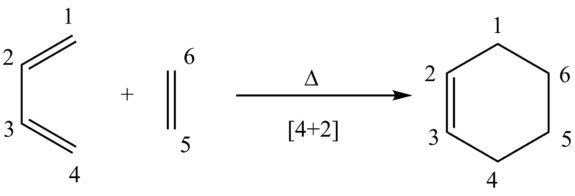
MO Diagram
From the visualised MOs in the table below and the MO diagram above, a conclusion can be made that only orbitals of the symmetry interact, i.e. symmetric-symmetric and anitsymmetirc-antisymmertic orbitals are able to interact. Interactions of like-symmetry are said to be allowed and interactions of opposite symmetry are symmetry-forbidden and disallowed. A further conclusion that can be drawn is that when MOs of like-symmtery combine they form a pair of MOs with the same symmetry. For example, the asymmetric combination of the butadiene HOMO and ethene LUMO produce an antisymmetric HOMO-1 and LUMO+1 pair.
The overlap integral produces a value from zero to one and quantitatively measures the overlap of two orbitals and how constructive or destructive an interaction is. A value closer to one, the more favourable and constructive the interaction. The overlap integral is zero when the orbitals (also wave functions) positive and negative aspects cancel out, for example, this occurs for a symmetric-antisymmetric interaction, hence why no such interaction is seen in the MO diagram. The integral is non-zero for like-symmetry interactions such as symmetric-symmetric and antisymmetric-antisymmetric. All interactions producing the transition state MOs visualised have come from a combination of reactant MOs with like-symmtery.
Observing how each of the electron pairs from the HOMOs of the reactants have changed to when occupying the HOMOs of the transition state, it's clear these electron pairs have gained energy. This is a result of the transition state having an energy barrier needed to be reached and overcome to form products.
Ethene MO's
| Ethene HOMO | Ethene LUMO | ||||
|---|---|---|---|---|---|
|
|
Butadiene MO's
| Butadiene HOMO | Butadiene LUMO | ||||
|---|---|---|---|---|---|
|
|
Transition state MO's
| TS HOMO-1 | TS HOMO | TS LUMO | TS LUMO+1 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
Variations in C-C bond lengths
Table 1: Bond lengths in the reactants, TS and products. (Look to reaction scheme for C atom numbering).
| C-C Bond | Butadiene
bond length/Å |
Ethene
bond length/Å |
TS
bond length/Å |
Cyclohexene
bond length/Å |
|---|---|---|---|---|
| C1-C2 | 1.34 | n/a | 1.38 | 1.50 |
| C2-C3 | 1.47 | n/a | 1.41 | 1.34 |
| C3-C4 | 1.34 | n/a | 1.38 | 1.50 |
| C4-C5 | n/a | n/a | 2.11 | 1.54 |
| C5-C6 | n/a | 1.33 | 1.38 | 1.53 |
| C6-C1 | n/a | n/a | 2.11 | 1.54 |
C-atom Van der Waals radius: 1.70 Å [4]
Typical sp3 C-C bond length: 1.54 Å [5]
Typical sp2 C-C bond length: 1.34 Å [5]
Firstly examining the C5-C6 bond variation, the bond length increases from ethene to the transition state and to finally the cyclohexadiene product. Both carbons in the bond start off with a sp2 hybridisation and end in the products as sp3 hybridised. The greater electron donation as the reaction progresses in to the ethene π* orbital increases the length of the bond until the π bond is broken and just a sigma bond remains. The initial C5-C6 bond length (1.33 Å) in ethene closely resembles the literature value (1.34 Å).
The C-C single bond in butadiene (C2-C3) is shorter than the literature value. This can be explained by the conjugation of the π system in butadiene, it increases the double bond character of the bond and therefore decreases the overall bond length. Observing this bond as the reaction progresses its bond length decreases and eventually a π bond is formed in the products. The C2-C3 double bond length in the product is consistent with literature. The C=C bonds in butadiene (C1-C2 and C3-C4) lengthen as expected as the they change from double to single bonds as the reaction progresses. The hybridisation of C2 and C3 stay unchanged (sp2) from reactants to product while C1 and C4 go from sp2 to sp3 hybridisation.
The C-C single bonds in the product have different bond lengths (1.54 Å and 1.50 Å), this is due some of the single bonds being between sp2 and sp3 centres. This shortens the C-C bond length.
For a bonding interaction to occur between two carbon atoms the distance between them has to be smaller than twice the Van der Waals radius of a C atom (3.40 Å). The partially formed bonds in the transition state (C4-C5 and C6-C1) meet this criterion, thus two new C-C sigma bonds are able to form.
Reaction path vibration at the transition state
Illustrated below is the reaction path vibration for the transition state. The vibration is imaginary which is consistent with being the vibration of the transition state. Furthermore, the vibration shows the formation of the two sigma bonds is synchronous. Both C-C bonds are formed simultaneously and in a concerted manner, as expected for a conventional Diels-Alder reaction.
Appropriate LOG Files
File:Ac4515-ex-1-OPTIMISED PRODUCTS- PM^.LOG
Exercise 2
Reaction Scheme

Transition State MO Diagrams
(Fv611 (talk) Again, very nice MO diagrams and good discussion.)
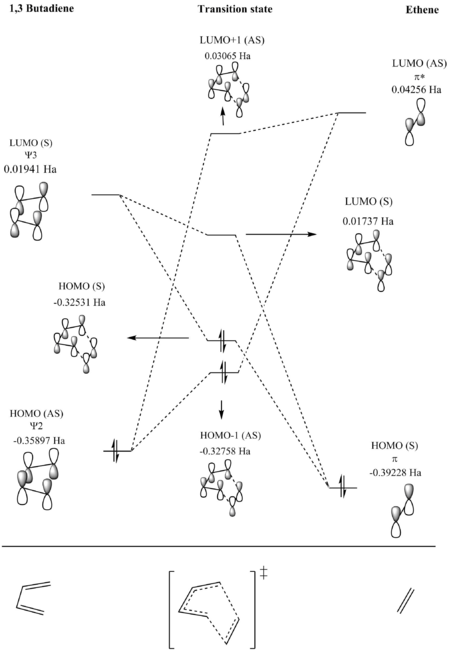
Examining both the MO diagrams below (figure 4 and 5), the interactions that are symmetry allowed are the symmetric combinations of the dieneophile (1,3 dioxole) HOMO and the LUMO of the diene (cyclohexadiene) producing the symmetric HOMO and LUMO molecular orbitals of the transition state. The other symmetry allowed interaction is between the antisymmetric combination of the HOMO of the diene and the LUMO of the dienophile producing the antisymmetric HOMO-1 and LUMO+1 molecular orbitals of the transition state. Similar to exercise one, the TS bonding MOs (HOMO and HOMO-1) are higher in energy than the HOMOs of the reactants they were produced from. Again, this is a result of the energy barrier between the reactants and transition state.
| Exo TS MO Diagram | Endo TS MO Diagram |
|---|---|
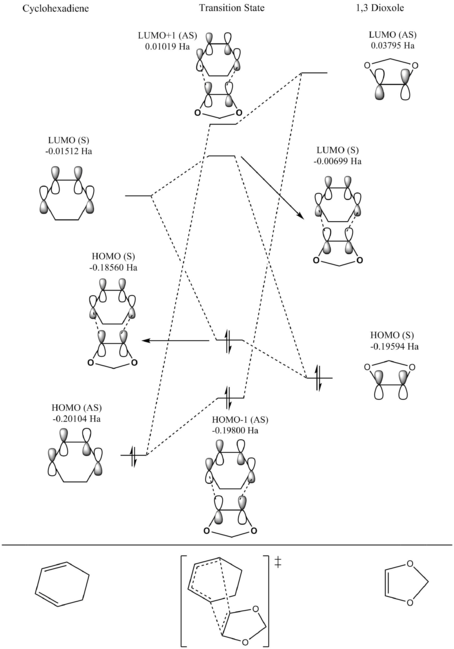 |
 |
| Exo TS HOMO-1 | Exo TS HOMO | Exo TS LUMO | Exo TS LUMO+1 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Endo TS HOMO-1 | Endo TS HOMO | Endo TS LUMO | Endo TS LUMO+1 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
Single point energy- Electron demand of the Diels-Alder reaction
A single point energy calculation was done to obtain an ordered list of the MO's of the diene (cyclohexadiene) and the dienophile (1,3 dioxole). In a conventional Diels-Alder pathway the diene and dienophile are electron rich and electron deficient respectively, this yields frontier orbitals with a HOMO supplied by the diene and the LUMO from the dienophile. This interaction is said to be a normal electron demand Diels-Alder.
For the Diels-Alder reaction of cyclohexadiene with 1,3 dioxole the opposite is the case: the diene is electron poor and the dienophile is electron rich. Therefore the frontier orbitals interacting strongly in this reaction are the HOMO of the dienophile and the LUMO of the diene (look to table 2) and the reaction is said to be an inverse electron demand Diels-alder. The electron demand of this reaction can be explained by the electron donation of the oxygen atoms on 1,3 dioxole (for a normal electron demand DA the dieneophile has an EWG substituent). The increased electron density given by the oxygen atoms raises the energy of the dienophile HOMO and LUMO resulting in a electron rich dienophile and an inverse electron demand.
Table 2: Relative energies of the HOMO and LUMO's of Cyclohexadiene and 1,3 Dioxole.
| MO | Energy / Hartrees | Jmol | ||
|---|---|---|---|---|
| HOMO Diene | -0.32217 | |||
| HOMO Dienophile | -0.32207 | |||
| LUMO Diene | +0.02111 | |||
| LUMO Dienophile | +0.02979 |
Thermochemistry
Table 3: Reaction barriers and reaction energies of DA pathways
| Pathway | Reaction Barrier
Hartrees |
Reaction Barrier
kJ/mol |
Reaction Energy
Hartrees |
Reaction Energy
kJ/mol |
|---|---|---|---|---|
| Exo Diels-Alder | +0.063852 | +167.64 | -0.024305 | -63.81 |
| Endo Diels-Alder | +0.060866 | +159.80 | -0.025674 | -67.41 |
Data tabulated in table 3 shows the endo pathway to have the lower reaction barrier (energy required to reach the TS) and the pathway that forms the energetically preferred product (lower reaction energy). The endo-pathway therefore leads to the kinetic and thermodynamic products for this particular Diels-Alder reaction.
The kinetic product forms via the lowest energy transition state. Due to the secondary orbital interactions (table 4 below) seen in the endo pathway and an absence of this effect in the exo pathway, there is a greater stabilising effect on the transition state via the endo route. In the endo HOMO the secondary orbital interactions come about as a result of the p orbtials of the oxygens having the correct orientation to interact with pi system of the diene fragment, thus having a stabilising effect overall. This effect is not seen in the exo HOMO as the p orbitals are not oriented properly for favorable overlap to occur.
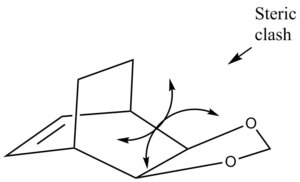
The most energetically stable product is the thermodynamic product, the exo product is disfavored energetically compared to the endo product due to a steric clash between the bridge of the cyclohexadiene ring and the di-oxygen ring (seen in figure 6) which causes the an increase in energy of the exo product. This type of steric clash is not seen in the endo product because the two rings are in different planes.
Table 4: Jmols showing secondary orbital interactions of the HOMO of the exo and endo transition states
| Exo TS HOMO | Endo TS HOMO | ||||
|---|---|---|---|---|---|
Appropriate LOG Files
File:Ac4515-B3-CYCLOHEXADIENE.LOG
File:Ac4515-exo-ex2-B3-TS-BERNY-3-POPGFULLPRINT.LOG
File:Ac4515-endo-B3-TS-BERNY-POPGFULLPRINT.LOG
File:Ac4515-exo-ex-2-IRC-PM6.LOG
File:Ac4515-endo-ex-2-IRC-PM6.LOG
File:Ac4515-exo-ex-2-B3-OPT-PRODUCTS.LOG
File:Ac4515-endo-ex-2-B3-OPT-PRODUCTS.LOG
File:Ac4515-ex-2-ENERGY-CALC-POP.LOG
Nf710 (talk) 21:59, 21 February 2018 (UTC) This was a very good section. It was excellent that you include the MOS of the single point energy. aand your energies were correct and you had some nice diagrams to complement your discussion.
Exercise 3
Diels-Alder at first diene fragment
Reaction Scheme
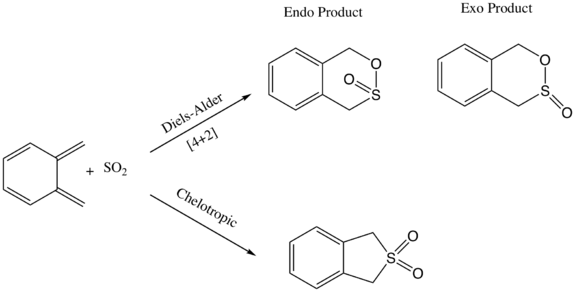
IRC's
Table 5: Visualisation of the reaction coordinate via IRC for reactions at the first diene fragment
| Exo DA IRC | Endo DA IRC | Chelotropic DA IRC |
|---|---|---|
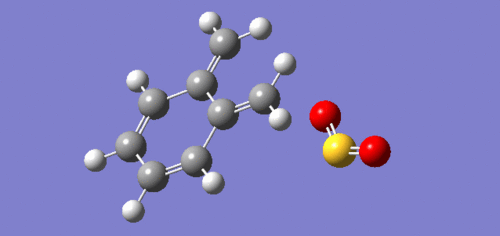 |
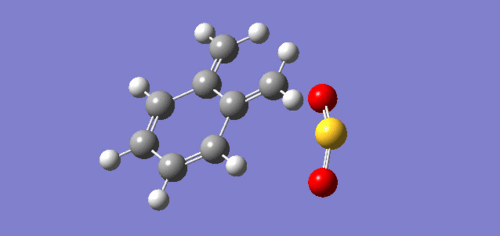 |
 |
The IRC's above in table 5 illustrate the reaction coordinate for each of the respective pathways. It can be seen that for all pathways, formation of the six-membered aromatic ring occurs before bonding with sulphur dioxide. This can be attributed to the high instability of xylylene and its eagerness to form a much more stable aromatic ring system. The chelotropic IRC shows a different trajectory and different bond formation than the two Diels-Alder reactions. The S-C bonds form simultaneously in the chelotropic reaction while in the Diels-alder reactions the bond forming steps happen separately.
Thermochemistry
Table 6:Thermochemistry data for the exo and endo diels-alder reactions
| Pathway | Reaction Barrier
Hartrees |
Reaction Barrier
kJ/mol |
Reaction Energy
Hartrees |
Reaction Energy
kJ/mol |
|---|---|---|---|---|
| Exo Diels-Alder | +0.032647 | +85.71 | -0.037978 | -99.71 |
| Endo Diels-Alder | +0.031131 | +81.73 | -0.037725 | -99.05 |
| Chelotropic | +0.039632 | +104.05 | -0.059432 | -156.04 |
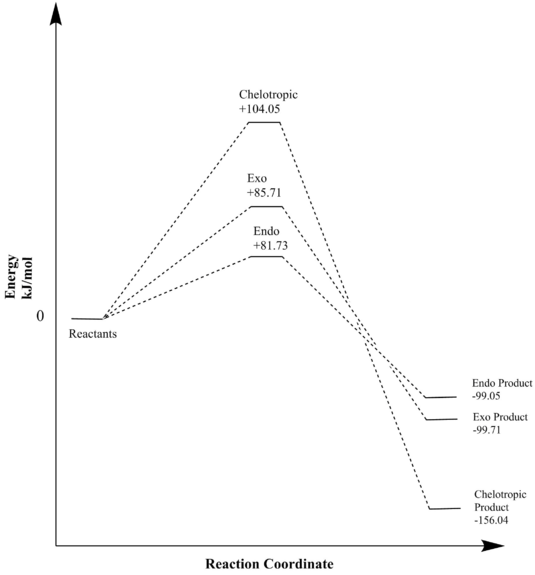
Thermochemistry data in table 6 and illustration of this in figure 8 shows that all three reactions are favourable (negative reaction energy) due to the aromatisation of the unstable xylylene. Furthermore, it is clear that reaction barrier for the chelotropic pathway is significantly higher than the two Diels-Alder reactions. Reasoning for this is the instability of the chelotropic transition state (determines reaction barrier), the transition state is a more unstable five-membered ring when compared to the more stable six-membered transition state formed via the Diels-Alder pathways. Now comparing the two reaction barriers of the two Diels-Alder reactions, it can be seen that the endo pathway has the lowest reaction barrier and is therefore the kinetic product. Similarly to exercise 2 (see above) this can be explained by the presence of the secondary orbital interactions seen in the endo pathway.
Observing table 6 it is clear to see the chelotropic route has the lowest reaction energy and thus forms the thermodynamic product. Presence of two strong S=O bonds (522 kJ/mol[6]) in the chelotropic product when compared to the one S=O bond in the Diels-Alder products is reason for it being the more stable, thermodynamic product. Depending on what conditions the reaction is under, the reaction will favor a different product. Under kinetic, non-reversible conditions the endo product will be favored and under thermodynamic, equilibrating conditions the chelotropic product will form.
Appropriate LOG Files
File:Ac4515-ex-3-DIENE-REACTANT-OPT-PM6.LOG
File:Ac4515-ex3-SO2-REACTANT-PM6.LOG
File:Ac4515-ex-3-OPTIMISE-EXO TS.LOG
File:Ac4515-ex-3-OPTIMISE-PRODUCTS-EXO.LOG
File:Ac4515-ex-3-ENDO PRODUCT.LOG
File:Ac4515-ex-3-IRC-CHELO.LOG
File:Ac4515-ex-3-OPT-TS-CHELO-CORRECT.LOG
File:Ac4515-ex-3-CHELO-OPT PRODUCT.LOG
Diels-Alder at alternative diene fragment
Reaction Scheme
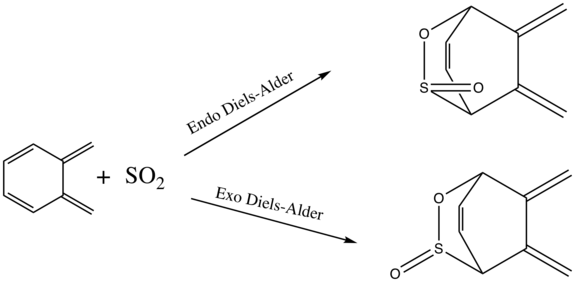
IRC's
Table 7: Visualisation of the reaction coordinate via IRC for reactions at the alternative diene fragment
| Exo DA IRC | Endo DA IRC |
|---|---|
 |
 |
Thermochemistry
Table 8: Thermochemistry data for the exo and endo diels-alder reactions at the alternative diene site
| Pathway | Reaction Barrier
Hartrees |
Reaction Barrier
kJ/mol |
Reaction Energy
Hartrees |
Reaction Energy
kJ/mol |
|---|---|---|---|---|
| Exo Diels-Alder | +0.045626 | +119.79 | +0.007874 | +20.67 |
| Endo Diels-Alder | +0.042641 | +111.95 | +0.006181 | +16.22 |
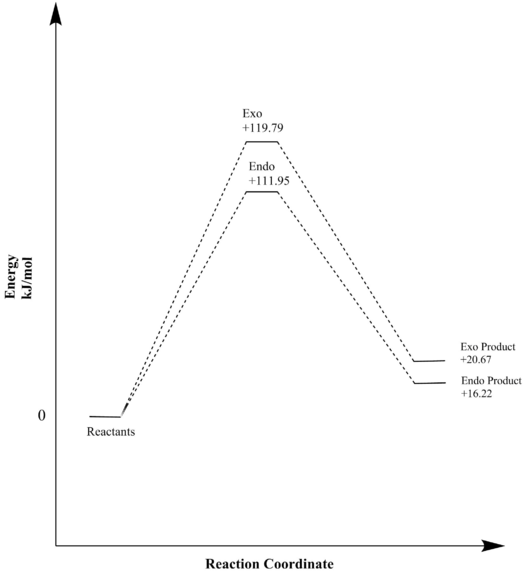
Shown by table 8 and figure 10 above the exo and endo reactions at the alternative site are both unfavorable and endothermic. The reaction barrier for these reactions are significant and so it can be concluded that both reactions are kinetically and thermodynamically unfavourable. No aromatisation of the products when compared to the reactions at the other diene site is reason for the high reaction barriers and energies seen. Therefore it is likely the Diels-Alder will always occur at the first diene site.
Even if these reactions are theoretical, the computed reaction barrier is still predicted to be lower for the endo pathway. Again this would be due to secondary orbital interactions in the endo route.
Appropriate LOG Files
File:Ac4515-ex-3-IRC-ALT-DA-EXO.LOG
File:Ac4515-ex-3-OPT-TS-ALT-DA-EXO.LOG
File:Ac4515-ex-3-OPT-PRODUCTS-ALT-DA-EXO.LOG
File:Ac4515-ex-3-IRC-ALT-DA-ENDO.LOG
File:Ac4515-ex-3-OPT-TS-ALT-DA-ENDO.LOG
File:Ac4515-ex-3-OPT-PRODUCTS.LOG
Further Work
Reaction Scheme

(I don't think this MO on the left exists in the FMOs. There's some rotation that goes on during the IRC that changes the pi and sigma orbitals. Tam10 (talk) 16:41, 23 February 2018 (UTC))
MO's
| Reactant
HOMO |
TS
HOMO |
Product
HOMO | ||||||
|---|---|---|---|---|---|---|---|---|
| Reactant
LUMO |
TS
LUMO |
Product
LUMO | ||||||
|---|---|---|---|---|---|---|---|---|
IRC
| Electrocyclic ring-opening |
|---|
|
Woodward-Hoffmann analysis
Woodward-Hoffmann equation: (4q+2)s + (4r)a
The reaction examined in this exercise can thought to be in equilibrium, with it shifted towards the less strained butadiene form (as oppose to the cyclobutene form). Since this is a pericyclic reaction it can be analysed via the principles of Woodward-Hoffmann. Where a thermal electrolytic reaction is allowed when the total count of the Woodward-Hoffmann equation is odd. Also where disrotatory and conrotatory electrolytic reactions have (4n+2)π and (4n)π electrons respectively. Since this reaction is reversible and in equilibrium, the type of rotation will be examined via the ring-closing reaction.

When examining reactions via Woodward-Hoffmann both the suprafacial and antarafacial can be considered to determine which route is allowed. In figure 12 both routes are shown for this particular example. In this relatively simple example it is clear by examination of the Woodward-Hoffmann equation above that the reaction proceeds antarafacially. The number of (4r)a antarafacial components would equal one and the (4q+2)s would equal zero, thus making the total of the components odd and therefore thermally allowed. If the reaction were to proceed suprafacially the total of both components would equal to zero and thus thermally disallowed. In an alternative photochemical scenario the antarafacial and suprafacial pathways would be disallowed and allowed respectively (opposite to what is seen thermally). Accounting for the type of rotation, since this a 4π system the reaction proceeds in a conrotatory fashion thus both ester groups end up on the same face in the cyclobutene fragment and trans to each other in the butadiene fragment.
Appropriate LOG Files
File:Ac4515-further-REACTANT-1-POP.LOG
File:Ac4515-further-work-TS-BERNY-CORRECT-POPGF.LOG
File:Ac4515-further-work-PRODUCT-OPT-POP.LOG
File:Ac4515-further-work-IRC-CORRECT.LOG
Conclusion
PM6 and B3LYP computations were successfully carried out to characterise and locate transition states for various pericyclic reactions. All exercises apart from exercise 2 were carried out with the semi-empirical method PM6. This less expensive method gave relatively accurate results and showed consistencies with literature, for example, the C-C bond lengths obtained in exercise 1. This therefore shows the methods validity in simple systems.
In exercise 2 the system was examined by the PM6 method first and then secondly by the more expensive DFT B3LYP method. When observing the validity of the two methods, the accuracy of B3LYP was shown to be greater.
Such computations are very useful in examining if reactions are feasible or not, this could save time and money when deciding if a reaction or synthetic route is worth investing in. For example, in exercise 2 it was seen that at the alternative diene fragment of xylylene the Diels-Alder would be highly unlikely to occur due to the high energetic barrier. Through computational software one is able to hypothesise such reactions, even if the reaction may not be plausible in reality.
Summarising, by the use of computational power it is relatively inexpensive to characterise a reaction when compared to obtaining such information empirically and thus is a very useful tool in chemistry today. However, relatively simple reaction pathways were examined in this task and so more complexed pathways would have to be investigated to see if the computational methods still worked with the same efficiency.
References
- ↑ 1.0 1.1 Lewars, E.G., 2016. Computational chemistry: introduction to the theory and applications of molecular and quantum mechanics. Springer.
- ↑ http://people.chem.ucsb.edu/kahn/kalju/chem226/public/semiemp_intro.html
- ↑ McDouall, J. J. W., 2013. Computational Quantum Chemistry, The Royal Society of Chemistry.
- ↑ https://www.cgl.ucsf.edu/chimera/docs/UsersGuide/midas/vdwtables.html
- ↑ 5.0 5.1 http://hydra.vcp.monash.edu.au/modules/mod2/bondlen.html
- ↑ http://www.chem.tamu.edu/rgroup/connell/linkfiles/bonds.pdf
