Rep:APL1995

Introduction

The transition state of a reaction is the state which corresponds to the largest potential energy along the reaction coordinate. At this point, the species can form the product(s) or it could ‘fall back’ to form the reactant(s). Transition states cannot be isolated and so cannot be studied directly. Despite this, the structure can be predicted by the Hammond Postulate which states the structure of the transition state resembles the reactants or products, depending on which it is closer in energy to. ‘Early’ transition states resemble reactants and ‘Late’ transition states resemble products. Hammond’s postulate cannot provide physical data, such as energy, bond lengths and angles. Computational chemistry is able to be used to find this physical data. The Gaussview program was used in this experiment with two methods used for this study, despite numerous methods being possible. The first was predicting the structure using the Hammond postulate and then optimising this to a minimum. The second method was the QTS2 method which involves drawing the reagents and products observed with a labelling scheme on the atoms. The calculation interpolates between the two species to find the associated transition state. The optimisation process and interpolation process has numerous levels of calculations which can be used but only a small number were used in this study. The HF/321-G level of theory was a basic, and quick, method to provide an answer with a reasonable level of accuracy. A more advanced method is the B3LYP/6-31G(d) which provides a more accurate result but with more time required for the calculation. Furthermore, the AM1 Semi-empirical method was used. The accuracy of these levels of theories differ with AM1 being the least accurate and B3LYP/6-31G(d) being the most accurate, due to the types of simplifications taken by each theory. This study will be looking at the Cope Rearrangement of 1,5-hexadiene, the Diels-Alder reaction of ethene and cis-butadiene, as well as the Diels-Alder reaction of cyclohexa-1,3-diene and maleic anhydride.

The Cope Rearrangement Tutorial

Background

Cope Rearrangement of 1,5-hexadiene

The Cope Rearrangement is a [3,3]- sigma-tropic rearrangement of a 1,5-diene. In this experiment, the Cope Rearrangement of 1,5-hexadiene will be considered and is shown in the diagram. In a pericyclic reaction, Woodward-Hoffmann rules can be used to show if a reaction is thermally allowed; if the total number of (4q+2)_s + (4r)_a components is odd (where q and r are whole numbers, s stands for suprafacial and a stands for antarafacial) then the reaction is allowed thermally. In this case, there are two _π2_a components and one _σ2_s components and so the reaction is thermally allowed. Furthermore, there is disrotation due to 6 electrons are moving around via Huckel topology with only suprafacial components.

Nf710 (talk) 15:56, 5 November 2015 (UTC) Good knowledge of the back groud of the reaction and the different pathway. clearly gone beyond the script.

Optimizing 1,5-hexadiene, the reactant and product

Optimisation of 1,5-hexadiene conformers using HF/3-21G theory

Initally the molecule of 1,5-hexadiene was drawn using the Gaussview program. To start, an 'anti' linkage is formed by changing the diahedral angle to 180 °. It is then optimized. The optimisation log file can be found here

Summary Data	Jmol

The energy of the 'anti' 1,5-hexadiene is -231.69253528 hartrees and the point group is C_i. This corresponds to the anti2 molecule found in the script's appendix.

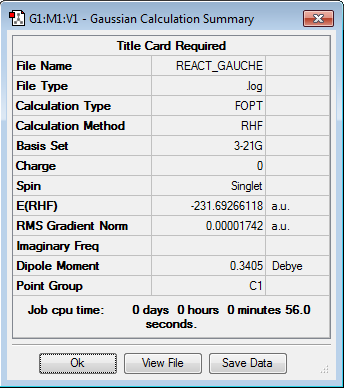
Then, a molecule of 1,5-hexadiene with a 'gauche' linkage was formed by changing the diheadral angle to 60 °. It is then optimized. The optimisation log file can be found here

Summary Data	Jmol

The energy of the 'gauche' 1,5-hexadiene is -231.69266118 hartrees and the point group is C₁. This corresponds to the gauche3 molecule found in the script's appendix.

Nf710 (talk) 16:00, 5 November 2015 (UTC) You havent spoke about why the gauche 3 conf is the lowest energy. It is due to the favourable interactions between the two pi bonds in the homo. If you wanted to prove this visually you can look at the orbitals in the .chk file to see this is the case.

Optimisation of a anti 1,5-hexadiene conformer using B3LYP/6-31G* theory and comparisons to HF/3-21G theory

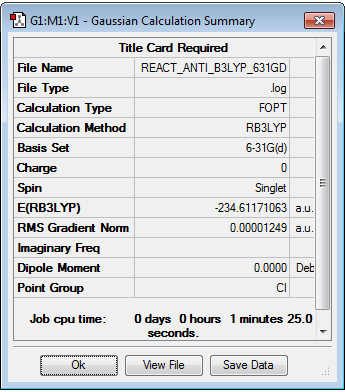
The 'anti' 1,5-hexadiene is then optimized at the B3LYP/6-31G* level. The optimisation log file can be found here

Summary Data	Jmol

Whilst the energies of the two molecules can not be compared as the 'zero level' for the energy differs between the HF method and the B3LYP method, the bond lengths and angles can be compared.

Bond Lengths

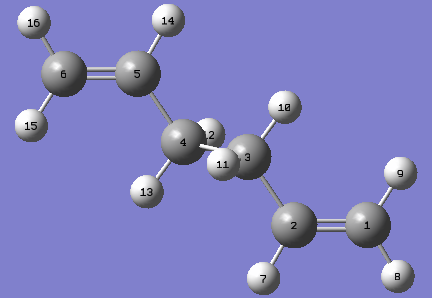Using the labelling system shown, the following data was obtained.

	Bond Lengths (Å)
Atoms	B3LYP	HF
C1-C2	1.33350	1.31613
C2-C3	1.50419	1.50891
C3-C4	1.54816	1.55275

The B3LYP gives a slightly longer C1-C2 bond than that from the HF theory. This longer bond is similar to the literature value of 1.33 Å. This infers that the B3LYP is a more accurate theory than HF. The C2-C3 bond lengths are similar in both cases and the C3-C4 bond lengths are close to theory. This suggests that the B3LYP theory should be used for unsaturated compounds but in saturated compounds, the HF theory would be sufficient.

Nf710 (talk) 16:04, 5 November 2015 (UTC) You are on the right track here. the pi bonds are better suited to be model by B3LYP as they take into account configurational effects of the delocalised pi electrons.

Bond Angles

Using the labelling system from the last section, the following data was found for the dihedral angles.

	Dihedral Angle (°)
Atoms	B3LYP	HF
C1-C2-C3-C4	118.600	114.669
C2-C3-C4-C5	180.000	180.000

The angles from theory would be 120 ° for an sp² system and so the B3LYP theory seems to be more suitable for this case.

Frequency analysis of an anti 1,5-hexadiene conformer

The frequency log file can be found here

Summary Data

The frequency analysis of a molecule will provide the second derivative of the potential energy surface with respect to the geometrical changes caused by a vibration. This can be used to find stationary points found from the optimized structure and also find if they are a maximum or a minimum. The minima would be corresponded to a positive frequency and maxima would be corresponded to an imaginary frequency. A transition state would have a single imaginary frequency.

Nf710 (talk) 16:07, 5 November 2015 (UTC) Some more info about where the imaginary frequencies come from would be nice. it is teh second derivative of the PES that gives the force constant in the quantum harmonic oscilator. it has k rooted in it. there if k is negative an imaginary frequecy with be returned

Optimizing the "Chair" and "Boat" Transition Structures

Optimizing the acyl fragments

In order to produce chair and boat transition structures, an acyl fragment would need to be optimized. The HF/3-21G theory was used and the results are shown below. The optimisation log file can be found here

Summary Data	Jmol

HF/3-21G Chair Optimisation

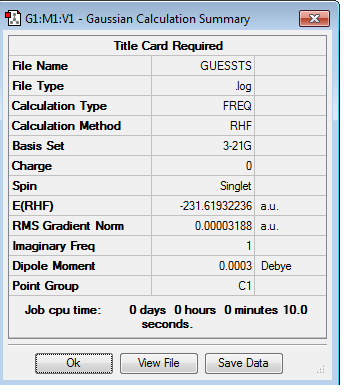
From the optimized acyl fragment, the chair transition state can be 'guessed' by placing two fragments approximately 2.2 Å apart in a staggered formation. The structure is optimized to transition state, rather than to a minimum, using the Berny algorithm. The results from this are found below. The optimisation and frequency log file can be found here

Summary Data	Jmol

Using the log file, it can be found that a stationary point is found and a chair transition state is formed. By looking at the frequencies for the vibrations, an imaginary frequency is found (with a value of -817.87 cm^-1). This shows that the stationary point is a maximum and so proves that this is a transition state structure.

Reaction Pathway Vibration

Frozen Coordinates Chair Optimisation

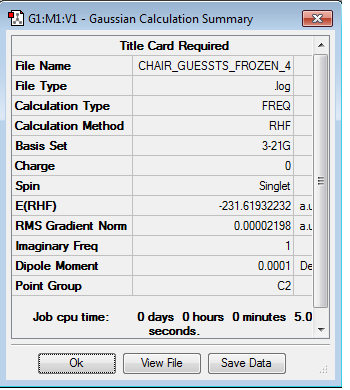
A different method used was the frozen coordinates method. In this part, the fragments are separated by 2.2 Å but the terminal carbons are fixed to be a distance of 2.2 Å with the rest of the molecule able to move to form an optimized structure. From this structure, the molecule is reoptimized with the whole molecule able to move but most of the optimization would be complete. The results are shown below. The optimisation and frequency log file can be found here

Summary Data	Jmol

A similar imaginary vibration is found with this method having a frequency of -817.88 cm^-1.

Reaction Pathway Vibration

Furthermore, the bond lengths of the bond forming and bond breaking bonds can be compared to the first method.

Method	Bond breaking length /Angstroms	Bond forming length /Angstroms
Guess	1.38931	2.02034
Frozen	1.38930	2.02073

Whilst the bond breaking lengths are very similar, the bond forming lengths are different with the frozen method providing a slightly larger length. However, it can be assumed that practically the same structure has been found in both methods.

QST2 Boat Optimisation

The boat transition structure was found with a different method than previously. The QST2 method involves drawing reactants and products of the reaction with labeling, as shown below. This method interpolates between the two structures to find the transition structure. The following labelling system was used:

Reagent Numbering	Product Numbering

A QST2 calculation was run with the HF/3-21G method. This leads to an unfavourable transition structure, shown below. It is unfavourable because it is geometrical impossible to occur. Furthermore, it does not produce the Cope Rearrangement but rather two acyl fragments are produced, followed by a translation to form a chair structure.

New structures are made which involve rotation of the central C-C bond to force the Cope Rearrangement to occur.

Reagent Numbering	Product Numbering

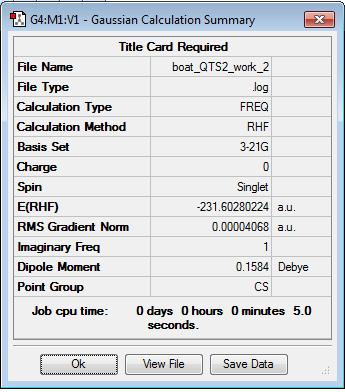
This process leads to the boat transition state structure be produced, as shown below.

The optimisation and frequency log file for the boat transition structure can be found here

Summary Data	Jmol

The stationary point is found to be a maximum with the vibration having an imaginary frequency of -840.22 cm^-1 and so corresponds to a transition structure of the Cope Rearrangement.

Reaction Pathway Vibration

Nf710 (talk) 16:10, 5 November 2015 (UTC)Nice use of JSmol and your frequencies are correct

IRC

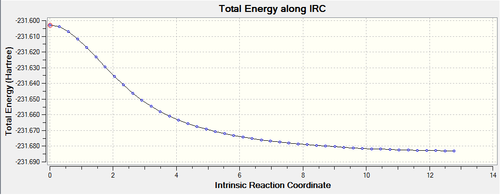
An intrinstic reaction coordinate (IRC) calculation can be found for the optimized transition state structures to find what conformer is initially produced in the reaction. The accuracy of the result is inversely proportional to the size step of each iteration. The size can be reduced by recording more points along the reaction coordinate. 50 points was found to be sufficient in this case. The reaction is symmetrical, as the reactant is the same as the product, meaning only the forward reaction is required for the calculations; this also reduces the computational work required. The optimisation log file can be found here for the boat transition structure. A total energy plot and a root mean square (RMS) plot can be produced with this calculation as shown below.

The total energy plot shows how the transition state changes to a lower energy towards a minimum of the system. The RMS plot shows the derivative of the total energy plot and when the value reaches zero, which indicates the product is produced.

Activation Energies

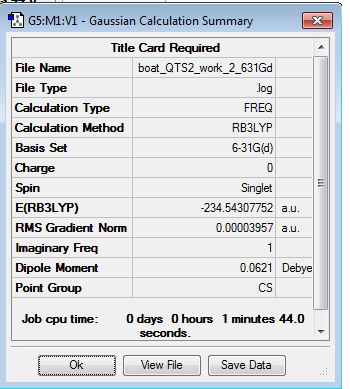
For the boat transition state, the structure is reoptimised with the B3LYP calculation using the QST2 method. Opt+Freq log file can be found here

Summary Data

There is one imaginary vibration with a frequency of -533.48 cm^-1.

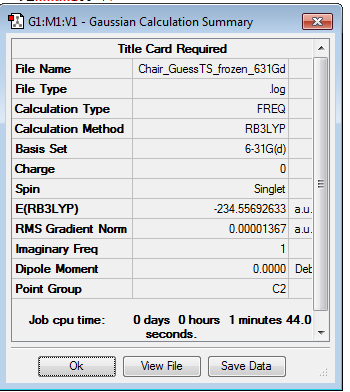
For the chair transition state, the structure is reoptimised with the B3LYP calculation using the Guess method. Opt+Freq log file can be found here

Summary Data

There is one imaginary vibration with a frequency of -569.84 cm^-1.

These are both still transition states. The thermochemical data obtained inside each log file is found below, with all units measured in Hartrees.

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies at 0 K	Sum of electronic and thermal energies at 298.15 K	Electronic energy	Sum of electronic and zero-point energies at 0 K	Sum of electronic and thermal energies at 298.15 K
Chair TS	-231.61932232	-231.466706	-231.461346	-234.55692633	-234.414918	-234.408986
Boat TS	-231.60280224	-231.450930	-231.445302	-234.54307752	-234.402337	-234.395999
Reactant (Anti2)	-231.692174743	-231.539539	-231.532565	-234.611711664	-234.469215	-234.461867

From this data, the activation energies can be found by finding the difference between the transition state and the product, which in case the anti conformer is being used. The units for the energy in this case have been converted to kcal/mol.

	HF/3-21G		B3LYP/6-31G*		Expt.
	0 K	298.15 K	0 K	298.15 K	0 K
ΔE (Chair)	45.7	44.7	34.1	33.2	33.5 ± 0.5
ΔE (Boat)	55.6	54.8	42.0	41.3	44.7 ± 2.0

Some key points that can be observed by finding the activation energies such as the B3LYP/6-31G(d) theory is more accurate than that for HF/3-21G theory. Furthermore, at 0 K, the amount of energy needed to reach the activation energy is slightly higher. This is due to the lack of additional thermal energy which can cause the molecule to be remain, on average, nearer to the minimum. Finally, in both levels of theory, the chair transition state occurs at a lower energy meaning it is the preferred pathway, in a kinetic sense.

16:17, 5 November 2015 (UTC) You have correctly computed the energies and frequencies. However you havent looked at the geometries which means you have deduced that the smaller basis sets are very good at getting the geometry but a larger basis set is need to get to the energy. In all in this report you haev done what is required of you, but it would have been nice if you could have showed some more understanding about what HF and DFT actually are.

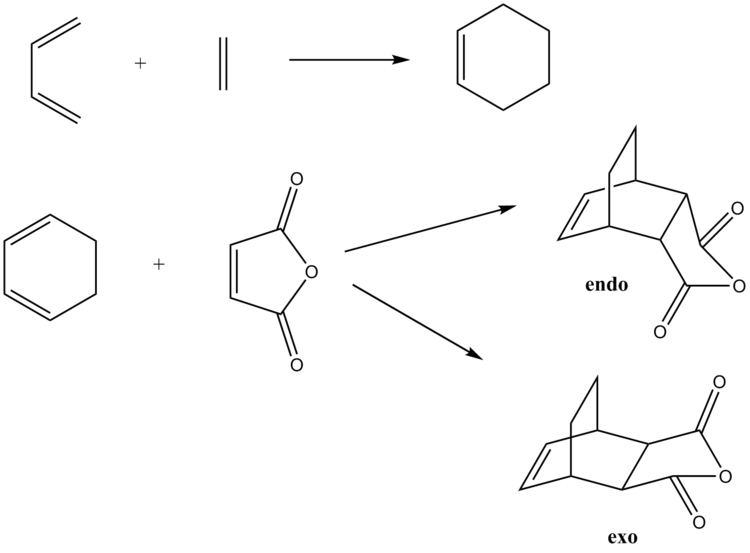
The Diels Alder Cycloaddition

Background

The Diels-Alder reaction is a [4+2] cycloaddition between a conjughated diene and a dienophile to form a cyclohexene-based system. The two reaction schemes of the reactions are shown below.

(Not really a big deal here, but you should get into the habit of labelling diagrams like this Tam10 (talk) 16:22, 28 October 2015 (UTC))

The reaction occurs as the two σ bonds are more stable than the π bonds which are broken.

Ethene/Cis-butadiene Diels Alder Reaction

Ethene Optimization

Ethene is optimized with the semi-empirical AM1 level of theory. The optimisation log file for ethene can be found here

Summary Data	Jmol

The HOMO and LUMO orbitals of the optimised molecule have been visualised in the table below.

HOMO orbital	LUMO orbital
Symmetric with respect to the plane	Antisymmetric with respect to the plane

Cis-butadiene Optimization

Cis-butadiene is optimized with the semi-empirical AM1 level of theory. The optimisation log file for cis-butadiene can be found here

Summary Data	Jmol

The HOMO and LUMO orbitals of the optimised molecule have been visualised in the table below.

HOMO orbital	LUMO orbital
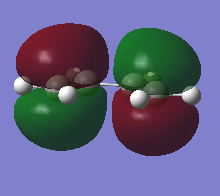Antisymmetric with respect to the plane	Symmetric with respect to the plane

Transition Structure Optimization

The optimized molecules are inserted and separated by a distance of approximately 1.5 Å. The optimisation log file for the transition structure can be found here

Summary Data	Jmol

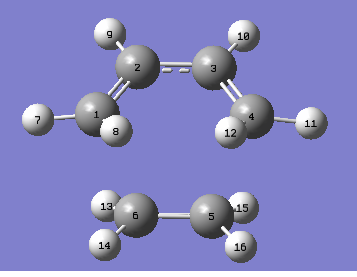The bond lengths are provided using the labelling system shown.

Atoms	Bond Lengths (Å)
C1-C2	1.38183
C2-C3	1.39748
C5-C6	1.38286
C1-C6	2.11885
C1-H7	1.09889
C2-H9	1.10183
C5-H15	1.09964

A sp³ C-C bond is approximately 1.54 Å and a sp² C-C bond is approximately 1.46 Å. As the bonds are closer in length to the sp² length, the carbons can be seen to be more similar to an sp² character. The Van der Waals radius of carbon is 1.70 Å. As the interaction between C5 and C6 is smaller than twice the van der Waals radius, there is an attractive interaction which could lead to the formation of a C-C σ bond. There is an imaginary vibration (-955.68 cm-1) found in the table of vibrations meaning the stationary point is a maximum and hence this is a transition state. The vibration is shown below.

Reaction Pathway Vibration

As can be seen from the vibration, the formation of the bonds are synchronous. Below is the lowest positive frequency vibration.

Reaction Pathway Vibration

(Nice use of JMols for vibrations Tam10 (talk) 16:22, 28 October 2015 (UTC))

This vibration does not seem to be involved in the bonding process, as the vibration is not in the direction of bond formation Using Frontier orbital theory described in the introduction, it can be found if the reaction can occur. If the HOMO of one reactant interacts to the LUMO of the other reactant in the transition state, then the reaction is allowed. The reaction of ethene and cis-butadiene will be considered using this method with the MOs of the transition structure and the reactants.

(Correct statements above, but written in a slightly messy way Tam10 (talk) 16:22, 28 October 2015 (UTC))

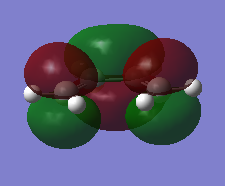
HOMO orbital	LUMO orbital
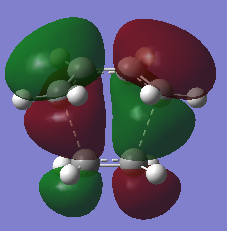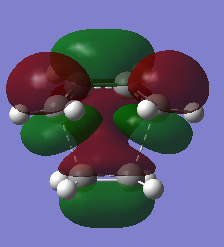
Antisymmetric with respect to the plane	Symmetric with respect to the plane

The HOMO of the transition state structure consists of the HOMO of cis-butadiene and the LUMO of ethene. Similarly, the LUMO of the transition state structure consists of the LUMO of cis-butadiene and the HOMO of ethene. This means the Diels-Alder cycloaddition can occur for ethene and cis-butadiene according to this theory.

Cyclohexa-1,3-diene/Maleic Anhydride Diels Alder reaction

Cyclohexa-1,3-diene Optimiziation

Cyclohexa-1,3-diene is optimized with the semi-empirical AM1 level of theory. The optimisation log file for cyclohexa-1,3-diene can be found here

Summary Data	Jmol

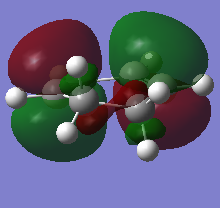
The HOMO and LUMO orbitals of the optimised molecule have been visualised in the table below.

HOMO orbital	LUMO orbital
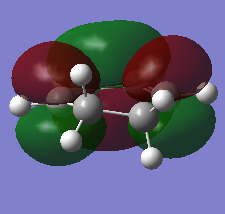
Antisymmetric with respect to the plane	Symmetric with respect to the plane

Maleic Anhydride Optimiziation

Maleic Anhydride is optimized with the semi-empirical AM1 level of theory. The optimisation log file for maleic anhydride can be found here

Summary Data	Jmol

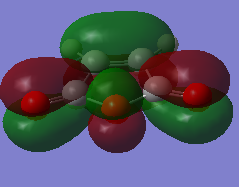
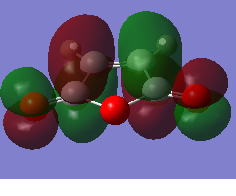
The HOMO and LUMO orbitals of the optimised molecule have been visualised in the table below.

HOMO orbital	LUMO orbital
Symmetric with respect to the plane	Antisymmetric with respect to the plane

Exo Transition State Optimisation

Optimized Cyclohexa-1,3-diene and maleic anhydride structures are inserted, separated by 2.2 Å in an exo fashion. It is optimized using the QST2 method with the semi-empirical AM1 level of theory. The optimisation log file for the exo transition state can be found here

Summary Data	Jmol

The stationary point is found to be a maximum as there is an imaginary vibration with a value of -812.10 cm^-1 inferring that the structure is a transition state. The vibration, shown below, corresponds to the Diels-Alder reaction.

Reaction Pathway Vibration

The HOMO and LUMO orbitals of the transition state structure have been visualised in the table below.

HOMO orbital	LUMO orbital
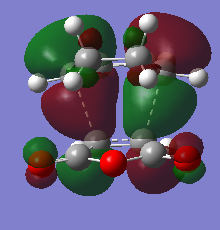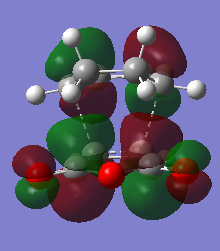
Antisymmetric with respect to the plane	Antisymmetric with respect to the plane

Endo Transition State optimisation

Optimized Cyclohexa-1,3-diene and maleic anhydride structures are inserted, separated by 2.2 Å in an endo fashion. It is optimized using the QST2 method with the semi-empirical AM1 level of theory. The optimisation log file for the endo transition state can be found here

Summary Data	Jmol

The stationary point is found to be a maximum as there is an imaginary vibration with a value of -806.35 cm^-1 inferring that the structure is a transition state. The vibration, shown below, corresponds to the Diels-Alder reaction.

Reaction Pathway Vibration

The HOMO and LUMO orbitals of the transition state structure have been visualised in the table below.

HOMO orbital	LUMO orbital
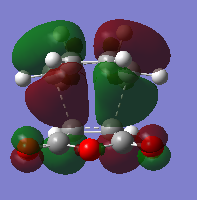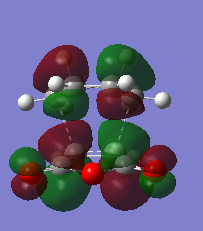
Antisymmetric with respect to the plane	Antisymmetric with respect to the plane

Comparison of transition state structures

Energy of conformers

Conformer	Energy (Hartrees)	Relative Energy (kcal/mol)
Exo	-0.05041983	0.68
Endo	-0.05150475	0

As the same theory was used to compute the transition structures, the energy can be compared. It can be seen that the endo conformer has a lower energy and so is the kinetic product of this Diels-Alder reaction.

Bond Lengths

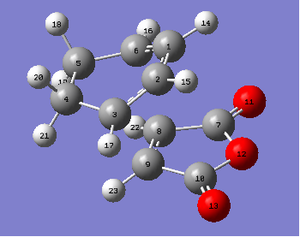
For the endo product, the following lengths were found using the numbering system to the right.

Atoms	Bond Lengths (Å)
C1-C2	1.39722
C2-C3	1.39303
C3-C4	1.49054
C4-C5	1.52299
C3-C9	2.16261
C8-C9	1.40850
C7-C8	1.48926
C5-C7	2.89223
C7-O11	1.22057
C7-C12	1.40895

For the exo product, the following lengths were found using the numbering system to the right.

Atoms	Bond Lengths (Å)
C1-C2	1.39678
C2-C3	1.39435
C3-C4	1.48971
C4-C5	1.52206
C3-C9	2.17061
C8-C9	1.41011
C7-C8	1.48819
C5-C7	2.94519
C7-O11	1.22053
C7-C12	1.40960

The σ bond being formed is slightly longer in the exo form than it is in the endo form. Furthermore, there is more steric repulsion in the exo form as the C5- C7 length is significantly larger in the exo form. This distance may be larger to reduce the energy of the molecule as there may be steric factors leading to an increase in energy. The maleic anhydride section of the molecule is likely to be more strained in the exo product.

Thermochemistry

Examining the thermochemistry part of the log file, the following energies can be found for the molecules at 298 K.

Molecule	Semi-empirical/AM1 Sum of electronic and thermal energies at 298.15 K /Hartree
Cyclohexa-1.3-diene	0.157725
Maleic Anhydride	-0.058192
Exo	0.144882
Endo	0.143684

From this data, the activation energy barrier can be found. For the exo transition state, it is 28.5 kcal/mol and for the endo transition state it is 27.7 kcal/mol. This further shows that the endo product is the kinetic product of this reaction.

Frontier Molecular Orbital Theory

One can use frontier molecular orbital theory to predict if the reaction will occur by considering the transition structure MOs and the reactant MOs. However, it seems that the MOs of the transition structure are not able to split it into the HOMO or LUMO of the reactants. This does not mean that the reaction does not occur as the reaction has been completed in the lab; this suggests that frontier molecular orbital theory is too simple for this case.

Secondary Orbital Overlap Effect

The secondary orbital overlap effect is the stabilization of a molecule due to π orbital overlap, rather than σ orbital overlap. In this case, this effect should lead to the endo product to have a lower energy because carbon π orbitals in the diene and the C=O π bonds should interact. In the HOMO, this would mean there would be an attractive interaction between the carbons in the diene component and the C=O orbitals. However, this calculation does not take this into account meaning there is not an attractive interaction.

Conclusion

In this study, the Cope Rearrangement and Diels-Alder reactions were investigated using Gaussian. The Cope Rearrangement was investigated for 1,5-hexadiene using a chair and boat transition state, which were modeled using different levels of theory, such as HF/3-21G and B3LYP/6-31G(d). It was found that the transition states had one imaginary vibration, with a negative frequency. These vibrations corresponded to the Cope Rearrangement. To finish this part, the activation energies were found and the B3LYP/6-31G(d) level of theory transition states were found to have values similar to experiment whereas the HF/3-21G level of theory was found to be a lot less accurate in finding the activation energy.

The Diels-Alder reaction of ethene + cis-butadiene and cyclohexa-1,3-diene + maleic anhydride were also modeled. In the ethene + cis-butadiene reaction, it was found that the frontier molecular orbital theory could be applied and the reaction was allowed. In the cyclohexa-1,3-diene + maleic anhydride reaction, it was found that the endo product had a lower activation energy barrier. It was found that the transition state for the exo product had more steric hindrance due to the longer distance between the two components. The frontier molecular orbital theory could not be used for this reaction, likely due to the fact that frontier molecular orbital theory being too simple for this molecule. Furthermore, it was found that the secondary orbital overlap effect was not taken into account with the semi-empirical AM1 level of theory.

To improve the experiment, asymmetric Cope Rearrangements could be studied and from that, the stereochemistry of this type of reaction. The Diels-Alder reactions could be further examined with a higher level of theory such as B3LYP/6-31G(d) to produce more accurate results. This could also be expanded further to test reactions which may not be thermal allowed, dictated by the Woodward-Hoffmann rules.