Potential control and current induced forces using CP2K+SMEAGOL

In this page I will discuss how to perform electronic structure calculations under potential control and with current induced forces using the newly developed CP2K+SMEAGOL interface. A paper based on this work has recently been submitted to the Journal of Chemical Theory and Computation. For comparison, I also include calculations performed using two different versions of SIESTA+SMEAGOL.

The CP2K+SMEAGOL interface is now included in the development branch of CP2K, with the corresponding SMEAGOL library available to download here . Currently, there is no publicly available version of SIESTA+SMEAGOL. Please request access to SIESTA1+SMEAGOL here and SIESTA3+SMEAGOL here .

This tutorial assumes some basic familiarity of NEGF calculations, please look elsewhere for an introduction to transport calculations.

Overview

Introduction

Figure 1. Example of a system setup in SMEAGOL: an extended molecule (Au-BDT-Au) attached to semi-infinite electrodes/leads (Au).

Figure 2. Flow chart how a standard DFT and a DFT-NEGF calculation may be setup: the DFT software generates a Hamiltonian which is then passed to a NEGF software to calculate the non-equilibrium density, from which a Hamiltonian can be calculated and this procedure repeats until self-consistency.

Figure 3. Structures of all examples. From top to bottom: Li chain, Au chain, Au capacitor, Au-H2-Au junction, Au-Melamine-Au junction. All systems are orientated with transport along the z-direction. The leads and extended molecule are separated with dashed black lines.

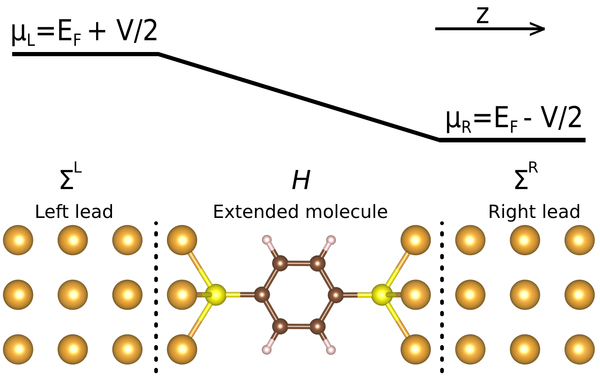
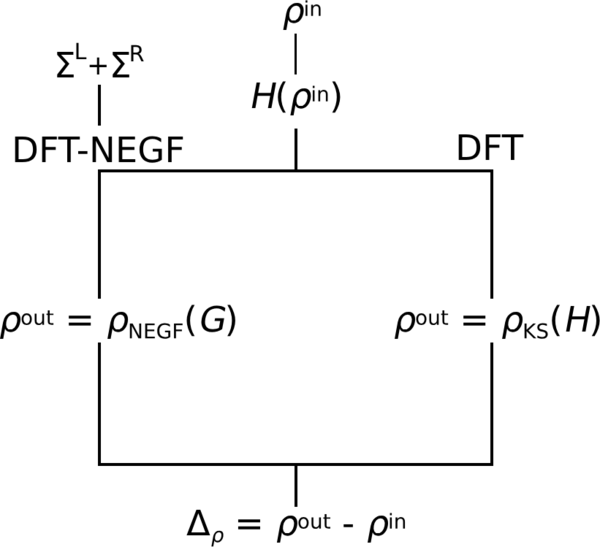
SMEAGOL is based on the non-equilibrium Green’s function (NEGF) formalism, transforming a periodic DFT calculation into an extended molecule attached to semi-infinite electrodes/leads. See Figure 1 for an example cartoon. This is performed by calculating a Hamiltonian in some DFT software and then passing this to a NEGF software to calculate the non-equilibrium density and then passing this back to the DFT software to calculate a new Hamiltonian, repeating until self-consistency. See Figure 2 for a flow chart. As such ideally a NEGF implementation should be platform agnostic, capable of being interfaced to any DFT software that uses localized basis sets such as CP2K or SIESTA. In practice I am aware of no platform agnostic NEGF implementations, as current codes such as SMEAGOL and TransSIESTA are strongly integrated into their corresponding DFT software. Plane wave codes such as VASP and Quantum Espresso are not generally able to perform NEGF calculations due to the requirement of defining local Hamiltonians and local Green's Functions, although some implementations have circumvented this limitation through the use of localised Wannier functions.

The original version of SMEAGOL was developed by the group of Stefano Sanvito , with current work lead independently by two of his former PhD students: Ivan Rungger and Alexandre Reily Rocha. The version of SMEAGOL used in this work was obtained from Ivan Rungger and is based on SEISTA version 1.3f1 2003. I therefore refer to this version as SIESTA1+SMEAGOL. For comparison, I also include some results using the version of SMEAGOL now developed by Alexandre Reily Rocha which uses SIESTA version 3.1 2011. I refer to this version as SIESTA3+SMEAGOL.

To the best of my knowledge there are no versions of SMEAGOL available for download, and the original website from the group of Stefano Sanvito no longer works . An archived version can be found on The Wayback Machine . Similarly, the SMEAGOL mailing list no longer works, but can an archived version be found on The Wayback Machine .

Starting with the version of SIESTA1+SMEAGOL obtained from Ivan Rungger, Sergey Chulkov developed a new platform agnostic version of SMEAGOL as well as an interface to the DFT software CP2K. I refer to this combination as CP2K+SMEAGOL. The motivation for developing CP2K+SMEAGOL was to modernise SMEAGOL and to allow for larger systems to be studied, in particular to use the MD capabilities of CP2K to perform large scale simulations of electrochemical systems under operating conditions.

Input file

A SMEAGOL calculation is composed of two steps. The first step is the calculation of the semi-infinite leads, which should be at least 3 layers thick in the transport direction. The CP2K &SMEAGOL section is very simple:

   &SMEAGOL
     PROJECT_NAME bulk
     BulkTransport  T
     BulkLead LR
   &END SMEAGOL

This results in a number of files being produced, most notably 'bulklft.DAT' and 'bulkrgt.DAT' which contain the information about the electronic structure of the leads and must be present for future SMEAGOL calculations. Unfortunately however 'bulklft.DAT' and 'bulkrgt.DAT' do not contain any information about the Hartree potential, which is important as the Hartree potential of the extended molecule and the leads must be aligned. In SIESTA+SMEAGOL the Hartree potential of the leads averaged along the transport direction is calculated using the provided script 'pot.sh', which uses the file '0.bulk.VH' to generate '0.bulk-VH_AV.dat'. In CP2K+SIESTA an equivalent file 'bulk-VH_AV.dat' is generated automatically. The value of the Hartree potential at z=0 can then be extracted and used in the extended molecule calculation. I use the following bash script to do this automatically, replacing 'HLB_REPLACE' in file '4_V.inp'

   HLB="$(grep '0.0000000000' bulk-VH_AV.dat | head -1 | awk '{print $2}')"
   sed -i -e "s/HLB_REPLACE/${HLB}/g" 4_V.inp

The &SMEAGOL section for the extended molecule calculation contains many keywords which control the NEGF calculation, activated with keyword 'EMTransport'. For a complete description of all parameters please refer to the SMEAGOL manual written by Ivan Rungger, as I will only discuss the most important keywords.

• 'NEnergReal' controls the number of evaluations of the Greens function along the real axis ${\mathrm{\Delta }}_{ij,\mathrm{n}\mathrm{e}\mathrm{q}}$. The corresponding values for the imaginary axis$D_{ij,\mathrm{e}\mathrm{q}}$ is 'NEnergImCircle' and 'NEnergImLine'. As the Greens function is smoother in the complex axis, 'NEnergReal' is chosen to be larger than 'NEnergImCircle' and 'NEnergImLine', and is the main keyword determining the accuracy and cost of the NEGF calculation. Generally the number of integrations along the complex contour is left at the defaults of 'NEnergImCircle' 16 and 'NEnergImLine' 16, while 'NEnergReal' must be increased from the default value of 0 to 64 or higher.
• 'VInitial' and 'VFinal' control the value of the potential, with 'NIVPoints' currently ignored in a CP2K+SMEAGOL calculation. In SIESTA+SMEAGOL this keyword allows an IV curve to be calculated without having to submit multiple jobs, however for technical reasons this is difficult to implement in CP2K.
• Delta refers to the value of ${\delta }_{+}$, an infinitesimal positive number required for broadening of the leads self-energies. Generally a value of 1e-4 is sufficient.
• EnergLowestBound refers to the start of the contour for evaluation of the Green's function. Generally a value of -100 eV is sufficient.
• 'TrCoefficients' enables printing of the transmission, where 'InitTransmRange' and 'FinalTransmRange' control the range of the transmission and 'NTransmPoints' controls the number of points.
• 'HartreeLeadsBottom' is the value of the Hartree potential of the leads evaluated to be used at 'HartreeLeadsLeft' and 'HartreeLeadsRight', which should be left at their default values of z=0.
• 'EM.ParallelOverKNum' controls the parallelism over kpoints. The default of 1 disables parallelism, while a finite value will divide the number of kpoints by the value of 'EM.ParallelOverKNum' across the MPI ranks. A value of -1 will automatically divide the number of kpoints by the largest factor allowed by the value of NEnergReal and MPI ranks (see following section for a discussion of SMEAGOL parallelism).

   &SMEAGOL
     PROJECT_NAME V
     EMTransport  T
     # Set number of energy points for integrals
     NEnergReal               64
     # Set bias range
     VInitial [eV]            1.0
     VFinal   [eV]            1.0
     NIVPoints                1
     # General variables
     Delta                    1e-4
     EnergLowestBound [eV]    -100
     # Print transmission coefficient
     TrCoefficients             T
     InitTransmRange [eV]     -10.0
     FinalTransmRange [eV]     10.0
     NTransmPoints            800
     # Matching of Hartree potential with the leads
     HartreeLeadsBottom [eV]  HLB_REPLACE
     # Other variables
     EM.ParallelOverKNum 1
   &END SMEAGOL

Parallelism

SMEAGOL is parallelised in four ways:

• MPI parallelism over NEnergReal (automatic)
• MPI parallelism over kpoints (requires EM.ParallelOverKNum)
• OpenMP parallelism over DO loops (automatic)
• OpenMP parallelism over matrix multiplication (automatic if provided by vendor)

Therefore the maximum number of cores that SMEAGOL will scale up to is NEnergReal*kpoints*omp_threads, for example 64*3*2=384 cores or 3 ARCHER2 nodes. As the system size increases the relative performance improvement with the number of OpenMP threads increases, however the bottleneck of matrix multiplication leads to the overall scaling O(N^3) such that large systems are incredibly expensive both in terms of CPU time and memory. As a comparison CP2K circumvents some of this scaling problem by using real space grids that scale with the size of the simulation box rather than the number of basis functions, and by using ScaLAPACK such that matrix multiplication and matrix diagonalisation can be paralleled more effectively through MPI. SMEAGOL does not support ScaLAPACK.

Compiling

An example of an automatic CP2K+SMEAGOL compilation script is available here for HPC SCARF, with the process explained below in greater detail.

An example of a SIESTA1+SMEAGOL arch.make is available here, and a SIESTA3+SMEAGOL arch.make is available here. From my experience, both versions of SIESTA+SMEAGOL have greater stability and performance using the Intel ifort compiler. As the Intel compiler is not available on ARCHER2, all SIESTA+SMEAGOL examples have been ran using the HPC YOUNG which uses ifort by default.

Before compiling CP2K with SMEAGOL support, please build the standalone SMEAGOL library first by running make program in its root directory. The supplied version of Makefile is gfortran-specific. In case of other compilers, please amend Makefile accordingly. The following preprocessor flags are likely needs to be defined as part of the Makefile’s FCFLAGS variable:

• -DNOSIESTA – disables SIESTA-specific parts (such as reading fdf input files) of the original SMEAGOL code;
• -DMPI – enables distributed-memory parallel version of SMEAGOL code. Must be enabled in case of distributed-memory parallel versions of CP2K, and disabled otherwise.

There is no need to run make install. Upon successful compilation, the standalone library libsmeagol.a can be found in lib directory created within the library’s root directory. The directory obj contains individual object files along with corresponding Fortran modules. Please do not remove this directory, as these Fortran module files are required to build the CP2K/SMEAGOL interface. To build CP2K with SMEAGOL support, the following changes need to be applied to CP2K’s arch file:

• Append -D SMEAGOL flag to DFLAGS variable;
• Append -I"/path/to/libsmeagol/obj" to FCFLAGS variable;
• Append -I"/path/to/libsmeagol/lib" to LDFLAGS variable;
• Prepend -lsmeagol to LIBS variable. The order of the libraries is important. Generally speaking, the SMEAGOL library should be linked with CP2K prior linking it with a LAPACK library.

Theory

This section is adapted from the QuantumATK implementation paper, which I find to be one of the clearest explanations of NEGF theory.

NEGF method

The key quantity to calculate is the retarded Green’s function matrix for the central region. It is calculated from the central-region Hamiltonian matrix $H$ and overlap matrix $S$ by adding the electrode self-energies $\mathrm{\Sigma }$,

   $G(ϵ)={[ϵ+i{\delta }_{+})S-H-{\mathrm{\Sigma }}^{\mathrm{L}}(ϵ)-{\mathrm{\Sigma }}^{\mathrm{R}}(ϵ)]}^{-1}$

where ${\delta }_{+}$ is an infinitesimal positive number. Calculation of $G$ at a specific energy $ϵ$ requires inversion of the central-region Hamiltonian matrix.

The electron density is given in terms of the electron density matrix. We split the density matrix into left and right contributions,

   $D=D^{\mathrm{L}}+D^{\mathrm{R}}$

The left contribution is calculated using the NEGF method as

   $D^{\mathrm{L}}=\int {\rho }^{\mathrm{L}}(ϵ)f\left(\frac{ϵ-{\mu }_{\mathrm{L}}}{k_B{T}_{\mathrm{L}}}\right)\mathrm{d}ϵ$

where

   ${\rho }^{\mathrm{L}}(ϵ)=\frac{1}{2\pi }G(ϵ){\mathrm{\Gamma }}^{\mathrm{L}}(ϵ)G^{†}(ϵ)$

is the spectral density matrix, expressed in terms of the retarded Green’s function and the broadening function of the left electrode,

   ${\mathrm{\Gamma }}^{\mathrm{L}}=\frac{1}{\mathbf{i}}({\mathrm{\Sigma }}^{\mathrm{L}}-({\mathrm{\Sigma }}^{\mathrm{L}}{)}^{†})$

Contour integration

This integral requires a dense set of energy points due to the rapid variation of the spectral density along the real axis. We therefore divide the integral into an equilibrium part, which can be integrated on a complex contour, and a non-equilibrium part, which needs to be integrated along the real axis, but only for energies within the bias window.

We have

   $D=D_{\mathrm{e}\mathrm{q}}^{\mathrm{L}}+{\mathrm{\Delta }}_{\mathrm{n}\mathrm{e}\mathrm{q}}^{\mathrm{R}}$

where

   $D_{\mathrm{e}\mathrm{q}}^{\mathrm{L}}=\int \mathrm{d}ϵ({\rho }^{\mathrm{L}}(ϵ)+{\rho }^{\mathrm{R}}(ϵ)+{\rho }^{\mathrm{B}}(ϵ))f\left(\frac{ϵ-{\mu }_{\mathrm{L}}}{k_B{T}_{\mathrm{L}}}\right)\mathrm{d}ϵ$

   ${\mathrm{\Delta }}_{\mathrm{n}\mathrm{e}\mathrm{q}}^{\mathrm{R}}=\int \mathrm{d}ϵ{\rho }^{\mathrm{R}}(ϵ)[f\left(\frac{ϵ-{\mu }_{\mathrm{R}}}{k_B{T}_{\mathrm{R}}}\right)\mathrm{d}ϵ-f\left(\frac{ϵ-{\mu }_{\mathrm{L}}}{k_B{T}_{\mathrm{L}}}\right)]$
 

where ${\rho }^{\mathrm{B}}$ is the density of states of any bound states in the central region.

Equivalently, we could write the density matrix as

   $D=D_{\mathrm{e}\mathrm{q}}^{\mathrm{R}}+{\mathrm{\Delta }}_{\mathrm{n}\mathrm{e}\mathrm{q}}^{\mathrm{L}}$

Due to the finite accuracy of the integration along the real axis the left and the right integrals are numerically different. It is therefore common practice to use a double contour

   $D_{ij}=W_{ij}^{\mathrm{L}}[D_{ij,\mathrm{e}\mathrm{q}}^{\mathrm{L}}+{\mathrm{\Delta }}_{ij,\mathrm{n}\mathrm{e}\mathrm{q}}^{\mathrm{R}}]+W_{ij}^{\mathrm{R}}[D_{ij,\mathrm{e}\mathrm{q}}^{\mathrm{R}}+{\mathrm{\Delta }}_{ij,\mathrm{n}\mathrm{e}\mathrm{q}}^{\mathrm{L}}]$

with weights $W_{ij}^{\mathrm{L}}$ and $W_{ij}^{\mathrm{R}}$ for each matrix element $ij$. In CP2K+SMEAGOL we use the same weights as TranSIESTA, using directly the non-equilibrium density to weight each matrix element individually

   $W_{ij}^{\mathrm{L}}=\frac{({\mathrm{\Delta }}_{ij,\mathrm{n}\mathrm{e}\mathrm{q}}^{\mathrm{L}}{)}^2}{({\mathrm{\Delta }}_{ij,\mathrm{n}\mathrm{e}\mathrm{q}}^{\mathrm{L}}{)}^2+({\mathrm{\Delta }}_{ij,\mathrm{n}\mathrm{e}\mathrm{q}}^{\mathrm{R}}{)}^2}.$

Forces

Figure 4. Li chain IV curve between -0.5 and 0.5 V (top), transmission for 0 V (middle), DOS for 0 V (bottom). Plotted using Python

The Hellmann–Feynman (HF) theorem expresses the total force acting on the $I$th atom $F_I$ as the negative derivative of the total energy $E$ with respect to its position $R_I$

   $F_I=-\frac{\partial E(R_I)}{\partial (R_I)}=-\frac{\partial ⟨\mathrm{\Psi }|\hat{H}(R_I)|\mathrm{\Psi }⟩}{\partial R_I}$

Expanding the derivative we find

   $F_I=[-⟨\mathrm{\Psi }|\frac{\partial \hat{H}(R_I)}{\partial R_I}|\mathrm{\Psi }⟩]+[-⟨\frac{\partial \mathrm{\Psi }}{\partial R_I}|\hat{H}(R_I)|\mathrm{\Psi }⟩-⟨\mathrm{\Psi }|\hat{H}(R_I)|\frac{\partial \mathrm{\Psi }}{\partial R_I}⟩]$

The first term is the well-known conventional HF force, and the second term is often referred to as the Pulay force. This vanishes only if $⟨\mathrm{\Psi }|$ is an exact eigenstate of $\hat{H}$ or if the basis set does not depend parametrically on the ionic coordinates (as for a plan-wave basis set).

This force can therefore be expressed as

   $F=F_{BS}+F_C$

Here $F_{BS}$ describes the force originating from the band structure (BS) contribution of the total DFT energy $E_{BS}$, which is equal to the sum of the eigenvalues of the occupied states. The second term $F_C$ is obtained by taking the derivative of the remaining contributions to the DFT total energy.

The BS force $F_{BS}$ can then be written as

   $F_{BS}=-\sum _{\mu v}{\rho }_{\mu v}\frac{\partial H_{\mu v}}{\partial R_I}+\sum _{\mu v}{\mathrm{\Omega }}_{\mu v}\frac{\partial S_{\mu v}}{\partial R_I}$

While it would be possible to simply calculate the forces in the usual manner in DFT by just using the nonequilibrium density matrix and Hamiltonian matrix, there is a second term involving the energy density matrix that must be included. The energy density matrix is calculated in the same manner as the density matrix, just with an additional factor $E$. I note that the contribution to the force arising from the energy density matrix is omitted in some NEGF implementations, such as SIESTA3+SMEAGOL by Alexandre Rocha (see Au chain section). For further discussion and extension to non-equilibrium cases please refer to Zhang et al.

Examples

I provide the following examples of CP2K+SMEAGOL and SIESTA+SMEAGOL calculations: Li chain, Au chain, Au capacitor, Au-H2-Au junction, Au-Melamine-Au junction and a solvated Au wire. These examples allow for a discussion of transmission, IV curves, Hartree potential and charge density as well the problem of bound states. For additional examples you may refer to the tutorial that Ivan Rungger wrote for IFT-UNESP . Unfortunately the lecture recordings for these tutorials are no longer available, however I included the exercises and lecture slides here.

Li chain (transmission, IV curve)

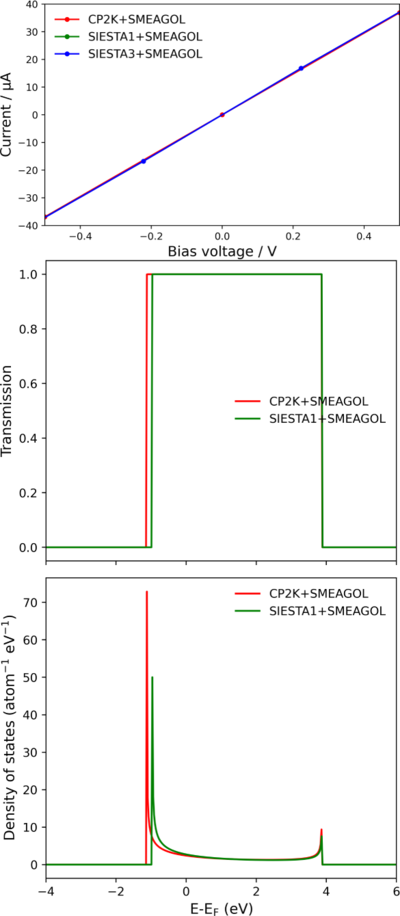
One of the simplest possible transport examples is an infinite chain of Lithium atoms. The leads are composed each of 4 atoms, and the extended molecule of 4*2+4=12 atoms. To check the results of the Li chain we can plot the transmission and density of states at 0 V and compare this with literature. This post-processing is performed by SMEAGOL, with the file '_TRC.agr' containing data for the: transmission, number of channels, EM DOS and leads DOS. The file can be automatically plotted using the visualisation tool Grace

   xmgrace 0.0V_TRC.agr

Some HPC clusters will support x11 forwarding such that xmgrace can be run directly on the HPC, otherwise Grace can be installed on your PC.

The plotted transmission and density of states (Figure 4) are in good agreement with literature results. The IV curve can then be calculated and the linear relationship between current and voltage confirmed as expected for an infinite 1D chain.

While SIESTA+SMEAGOL can calculate an IV curve in a single calculation using NIVPoints keyword, CP2K+SMEAGOL does not have this ability. As such to calculate the IV curve I use a bash script to automatically generate the required folders from a template file, see example here. Finally, only the IV curve is shown for SIESTA3+SMEAGOL as there is no TRC.agr file generated by SIESTA3+SMEAGOL and no documentation available to indicate if there is a keyword to enable printing.

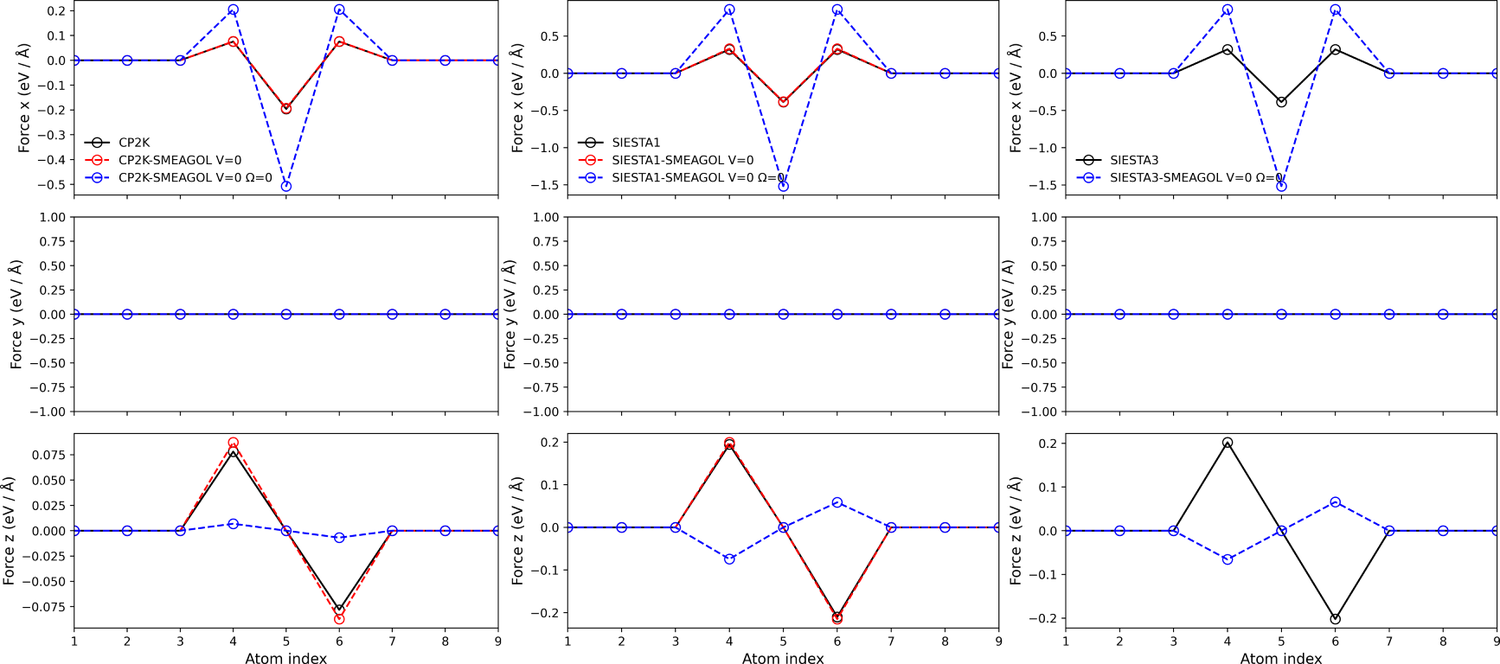
Au chain (forces)

In this example show a zero bias test for the atomic forces on a Au chain, reproducing the work of Zhang et al.. The Au chain is composed of 3*2+3=9 atoms, where the atoms belonging to the leads are frozen. The central Au atom is displaced by 1 A in the +x direction, such that there is a restoring force acting towards the equilibrium position. The x, y and z components of the force are shown below for CP2K+SMEAGOL, SIESTA1+SMEAGOL and SIESTA3+SMEAGOL. SIESTA3+SMEAGOL shows the results of a NEGF calculation which does not include the contribution from the energy density matrix $\mathrm{\Omega }$, causing qualitatively incorrect forces. With the inclusion of the force calculated from the energy density matrix in CP2K+SMEAGOL and SIESTA1+SMEAGOL it is clear that the zero bias forces are consistent with the CP2K and SIESTA forces.

Figure 5. Au chain forces for 0 V for CP2K+SMEAGOL (left), SIESTA1+SMEAGOL (middle) and SIESTA3+SMEAGOL (right). Plotted using Python

Au capacitor (bound states)

Figure 6. Au capacitor Hartree potential and charge density for CP2K and CP2K+SMEAGOL (left), and the difference between V=4 and V=0 for CP2K+SMEAGOL, SIESTA1+SMEAGOL and SIESTA4+SMEAGOl (right). Plotted using Python

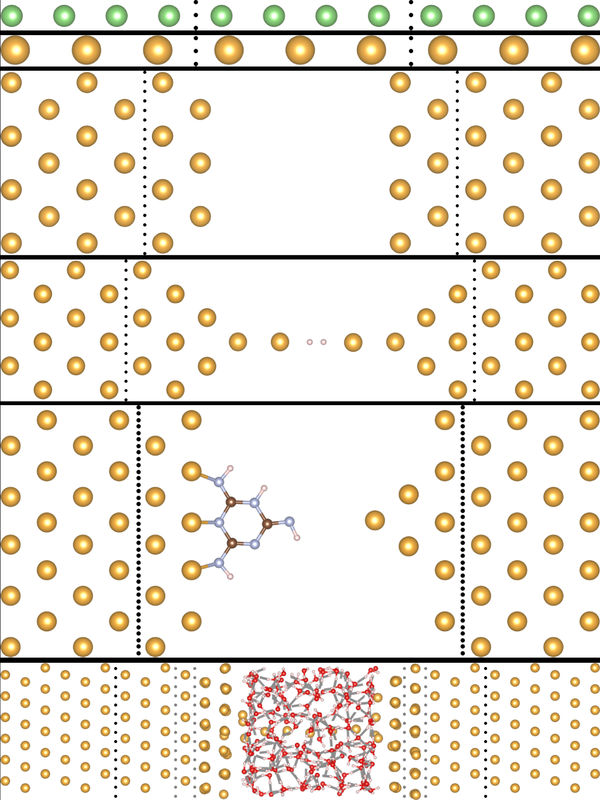
The Au capacitor is a useful system for confirming the correct behaviour of the Hartree potential and electron density in vacuum. The system structure is shown in Figure 3, composed of two 2x2 Au slabs (001) with 6 layers (left) and 6 layers (right) separated by 12 Å vacuum. The total number of atoms is 96 atoms, and therefore this is a more expensive system than the previously studied Li and Au chains.

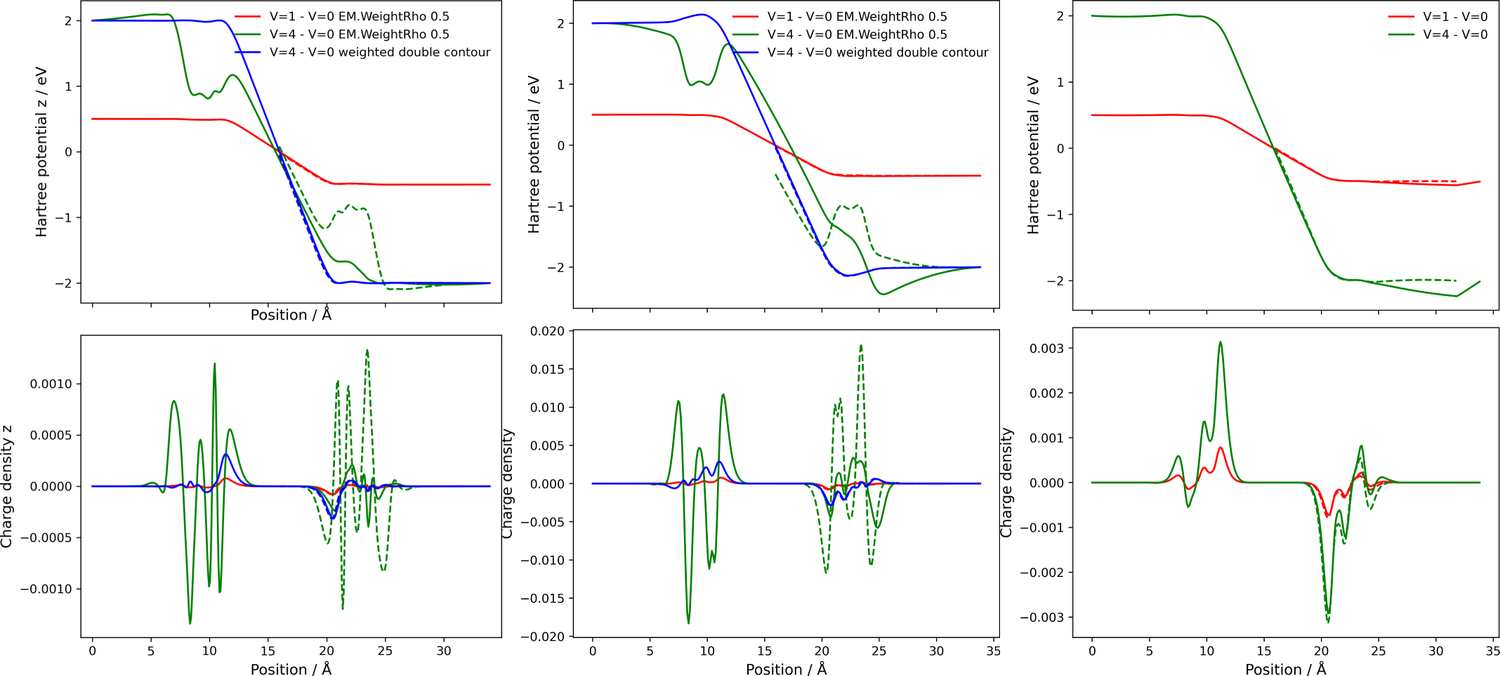
Figure 6 shows the Hartree potential and charge density along the transport direction for the CP2K+SMEAGOL leads, standard CP2K and CP2K+SMEAGOL at V=0 and V=4. The Hartree potential of CP2K is different to CP2K+SMEAGOL, highlighting the importance of 'HartreeLeadsBottom'. As the Hartree potential is only defined up to a constant, the use of 'HartreeLeadsBottom' is essential to ensure that the Hartree potential of the leads and extended molecule are consistent. The Hartree potential of 'CP2K+SMEAGOL bulk' and 'CP2K+SMEAGOL V=0' overlap, indicating the correct use of 'HartreeLeadsBottom'. As such, I generally recommend that the first step of any SMEAGOL calculation should be to plot the Hartree potential and charge density for 0V and ensure that there is correct alignment with the leads. A further check can be to ensure that the total charge in the system is 0.0, as a finite charge may indicate a failure of the SMEAGOL calculation. Also shown in Figure 6 is the Hartree potential and charge density for CP2K+SMEAGOL, SIESTA1+SMEAGOL and SIESTA4+SMEAGOL. While there are some quantitative differences such as the change in charge density at the interface with vacuum and the decay towards the leads, qualitatively the electronic structure is consistent.

Figure 7 shows the difference in the Hartree potential and charge density along the transport direction for 'V=1 - V=0' and 'V=4 - V=1'. It is clear that for CP2K+SMEAGOL and SIESTA1+SMEAGOL the Hartree potential and charge density labelled 'V=4 - V=0 EM.WeightRho 0.5' is qualitatively incorrect, with a clear asymmetry between the left and right electrodes. To highlight this further I show as a dotted line a mirror image of the Hartree potential and charge density, which should overlap with the solid line as the left and right electrodes are identical. This is the case for the results labelled 'weighted double contour'.

The asymmetry in the Hartree potential and charge density is a problem of bound states, states in the extended molecule with no coupling to the leads. In thesis Ivan Rungger identified bound states as a problem for SMEAGOL and proposed a bound state correction scheme which attempts to automatically identify and populate the bound states, however I have been unable to successfully use this unpublished and largely undocumented correction scheme. Instead, I recommend my newly implemented weighted double contour as used in TransSIESTA, QuantumATK and SIESTA3+SMEAGOL. The weighted double contour involves calculating the density by considering both the left and right electrodes, and using directly the non-equilibrium density to weight each matrix element individually (as described in the earlier theory section). The keyword 'EM.WeightRho' as implemented by Ivan Rungger instead sets the weight $W_{ij}^{\mathrm{L}}$ to a constant, producing a qualitatively incorrect electronic structure.

Figure 7. Au capacitor Hartree potential and charge density for CP2K+SMEAGOL (left), SIESTA1+SMEAGOL (middle) and SIESTA3+SMEAGOL (right). Plotted using Python

Au-H2-Au junction (geometry optimisation)

This example reproduces the geometry optimisation of a Au-H2-Au junction under bias as reported by Bai et al. . The system is composed of two 3x3 Au slabs (100) with 7 layers (left) and 6 layers (right) and 2 H atoms with a total of 113 atoms. The kpoint grid for the leads is 3x3x20 and for the extended molecule is 3x3x1, therefore I use EM.ParallelOverKNum 3 to exploit parallelism over kpoints. To further accelerate the geometry optimisation I use 'OMP_NUM_THREADS=2' with 'cpus-per-task=2'. All atoms are constrained in the system except for the 2 H atoms and the 6 Au atoms either side. I note that in the original publication Bai et al. state that there are "six atoms included in the dynamic region", however on inspection of the SIESTA input files used for the calculation it is clear that there are 14 atoms included in the dynamic region: the 2 H atoms, the 2 Au either side forming a Au-Au-H-H-Au-Au chain and then the 4 Au atoms either side forming which form the tip of the electrodes.

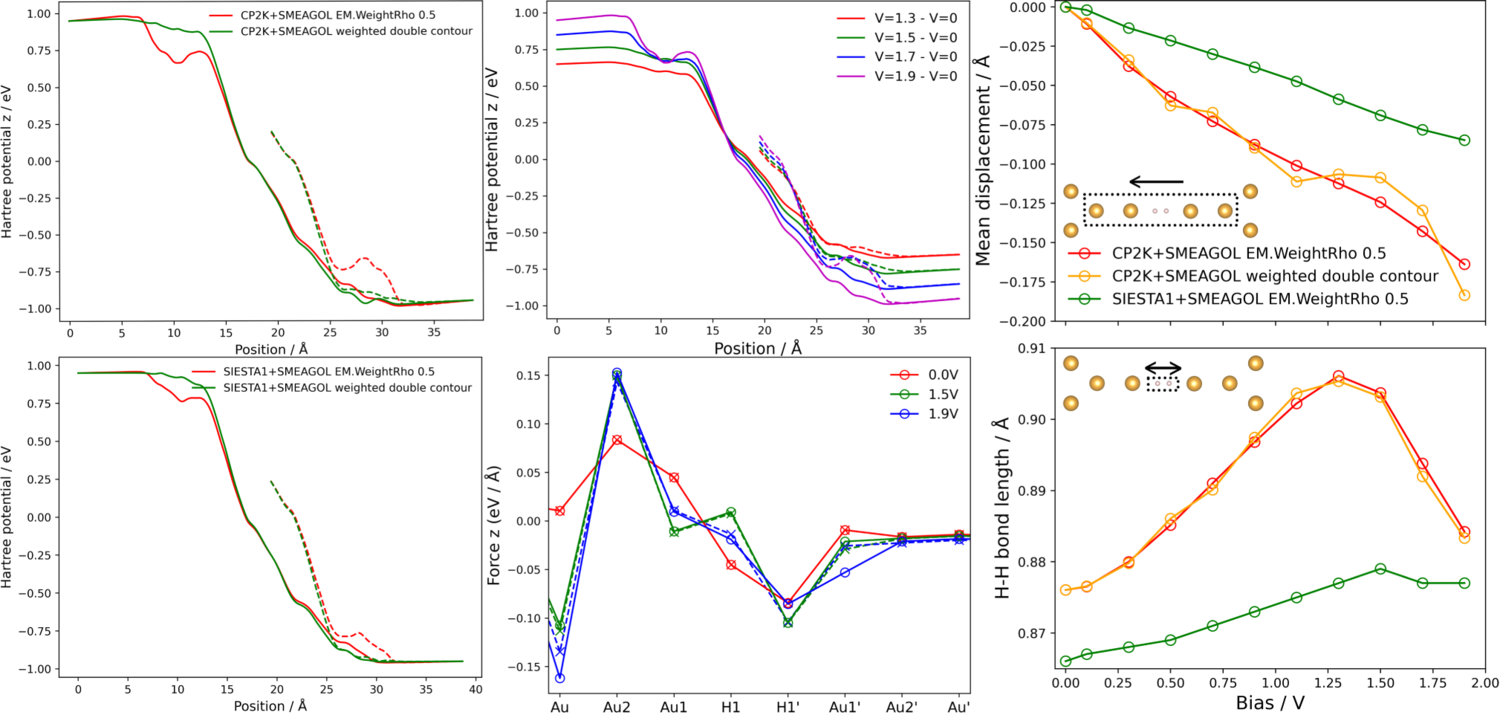
As previously discussed, the first step is to show that the electronic structure for V=0 is correct. Figure 8 (left) shows the Hartree potential and charge density for CP2K+SMEAGOL, with the correct alignment of the Hartree potential. The second step is to check for the presence of any bound states, Figure 8 (middle) shows the Hartree potential difference for CP2K+SMEAGOL (top) and SIESTA1+SMEAGOL (bottom) at the maximum bias of V=1.9 for both 'EM.WeightRho' 0.5 and using a weighted double contour, the lines do not overlap and there is an asymmetry similar to the earlier Au capacitor indicating the presence of bound states. Note that unlike the Au capacitor the Au-H2-Au system is not symmetric, and therefore the solid and dotted lines do not overlap at the centre. Importantly, the weighted double contour solid and dashed lines overlap at the interface between the extended molecule and leads while the 'EM.WeightRho' 0.5 do not. The charge density difference is not included as the geometric asymmetry causes a highly asymmetry charge density difference, providing no useful information.

Figure 8 (right) shows the mean displacement of the unconstrained atoms against the current flow, and the elongation of the H-H bond for both CP2K+SMEAGOL and SIESTA+SMEAGOL. While there are some minor differences, there is a qualitative agreement for geometry re-optimisation under bias for CP2K+SMEAGOL and SIESTA1+SMEAGOL. There is no difference in the results for 'EM.WeightRho' 0.5 and weighted double contour, which is consistent with the Hartree potential where the disagreement only occurs at the boundary between leads and extended molecule where the atoms are frozen. No results are given for SIESTA3+SMEAGOL as the forces no not include the contribution from the energy density matrix $\mathrm{\Omega }$, see earlier section Au chain (forces).

Figure 8. Hartree potential and charge density difference between V=1.9 and V=0 for CP2K+SMEAGOL (top left) and SIESTA+SMEAGOL (bottom left), Hartree potential difference for CP2K+SMEAGOL (top middle) between V=1.3 and V=1.9, z component of forces on atoms in dynamic region for CP2K+SMEAGOL with V=0, V=1.5 and V=1.9 (middle bottom) and geometry optimisation under bias for CP2K+SMEAGOL and SIESTA1+SMEAGOL (right). Plotted using Python

Au-Melamine-Au junction (NEB)

This example reproduces the change of activation barrier for switching between the C1 and C2 structures of melamine absorbed onto an Au(001) surface, aiming to reproduce the work of Ohto et al.. and Pan et al.. The C1 structure is shown in Figure 3 with an arrow indicating the 180 degree rotation of the N-H bond to form the C2 structure.

While the original works use Cu(001), this has been found to be problematic for CP2K+SMEAGOL. The Cu basis set in CP2K is more diffuse than Au, and therefore requires the use of larger cells to satisfy the requirements for a NEGF calculation. In SIESTA this is not a problem as the basis sets have a very short range cutoff of around 3 Å, while in CP2K even the short range basis sets result in finite density up to 6 Å away from the atom. In addition, Cu has a short lattice constant of 3.61 Å instead of 3.94 Å, exacerbating this issue further.

DFT geometry optimisations are performed with frozen Au atoms as well as the N atoms directly connected to the Au surface. The energies of the optimised GS, C1 and C2 structures are in good agreement between CP2K, SIESTA and the reference calculations performed in SEISTA and VASP. The transition state structure TS2 is obtained by performing a CI-NEB calculation starting from the optimised C1 and C2 geometries with the transition state guess generated manually. CP2K does not support frozen atoms with NEB, and therefore the atoms that should be frozen are allowed to move during the CI-NEB calculation, and then replaced with their unoptimized positions. As such, the TS2 structure energy is slightly higher than the reference calculations.

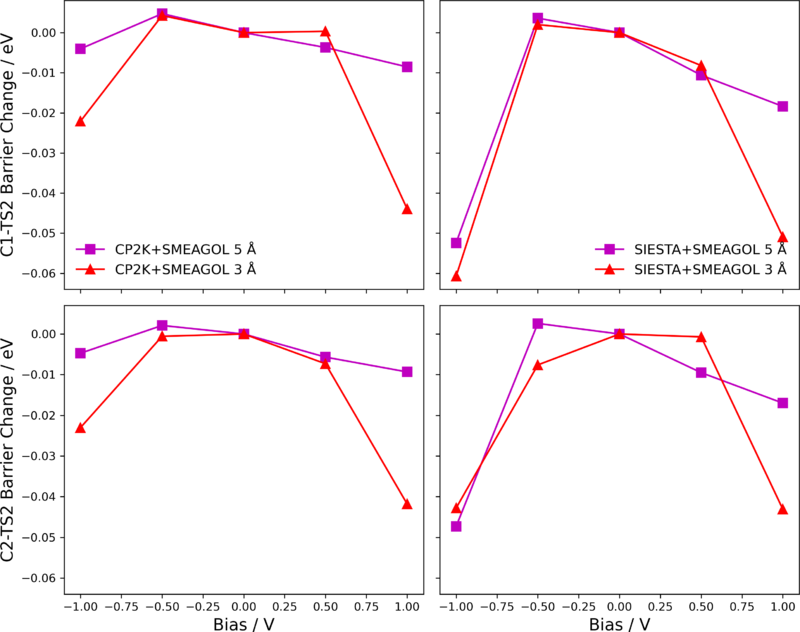
Figure 9 shows the change of activation barrier C1-TS2 and C2-TS2 under finite bias, with qualitative agreement between CP2K+SMEAGOL and SIESTA1+SMEAGOL. The change in C1-TS2 from -0.5 to 0.5 V in CP2K is 8 meV and in SIESTA+SMEAGOL is 14 meV, reasonable agreement when considering that these energy differences are on the same order of magnitude as numerical error in a standard DFT calculation.

Figure 9. Change of activation barrier C1-TS2 and C2-TS2 under finite bias. Calculations are performed for CP2K+SMEAGOL (left) and SIESTA1+SMEAGOL (right). Plotted using Python

	Au CP2K / eV	Au SIESTA / eV	Cu SIESTA / eV	Cu VASP / eV
GS	0.00	0.00	0.00	0.00
C1	0.77	0.71	0.72	0.71
TS2	2.01	1.82	1.70	1.77
C2	1.05	0.95	0.95	0.95

Au-wire-Au junction (MD)

The Au-wire-Au structure is based on work from a previous Master's student in our group Jad Jaafar, please refer to his thesis for information concerning his system setup. To allow for SMEAGOL transport calculations I made a number of modifications made to his structure and computational setup: TZVP basis sets were reduced to DZVP, and 6 layers of SZ (6s only) Au(111) atoms were added for the bulk. The use of 6 layers is necessary as the repeating blocks for the Au(111) surface are ABC, requiring a larger bulk then the Au(001) surface where the repeating units are AB. As a minimum of 4 layers are generally required in the bulk, this necessitates the use of 6 layers for the Au(111) surface. I also added an additional 3 layers of SZ (6s only) Au(111) in between the leads and extended molecule as a screening region, as otherwise a spurious build-up of charge density can occur at the interface of the leads and extended molecule where the basis set changes. A single layer of Au SZ (6s, 5d) is included between the screening region and extended molecule, such that the sub-surface Au layer at least has a full valence structure. All Au atoms are frozen except for the atoms belonging to the Au wire and first Au surface, which are all DZVP. An image of the system structure denoting the separation of each region is shown in Figure 3.

As CP2K+SMEAGOL is around 20x more expensive than a corresponding CP2K calculation, performing MD is very costly. In addition, wavefunction propagation which is used to accelerate standard MD calculations does not work well with SMEAGOL. The gold standard wavefunction propagator in CP2K is the always stable predictor corrector (ASPC), which is not implemented for kpoints. While the Au-wire-Au system only uses gamma point sampling of the Brillouin zone, due to technical limitations we must use the kpoint code in CP2K to interface with SMEAGOL and therefore are not able to the ASPC. The main alternatives to ASPC compatible with kpoints are USE_PREV_P and LINEAR_P which linearly mixes the previous density matrices. Unfortunately with CP2K+SMEAGOL it is found the USE_PREV_P and LINEAR_P work well for geometry optimisation or molecular dynamics with small systems, but for large solvated systems the default USE_GUESS is actually more robust and necessary to avoid convergence to the incorrect electronic state. While poor convergence in a typical MD calculation is generally not an issue as the forces will be approximately correct, for CP2K+SMEAGOL convergence to the wrong electronic state can often result in the loss of thousands of electrons and subsequently an explosion of the system. Consequently, only very short MD trajectories can be afforded with CP2K+SMEAGOL.

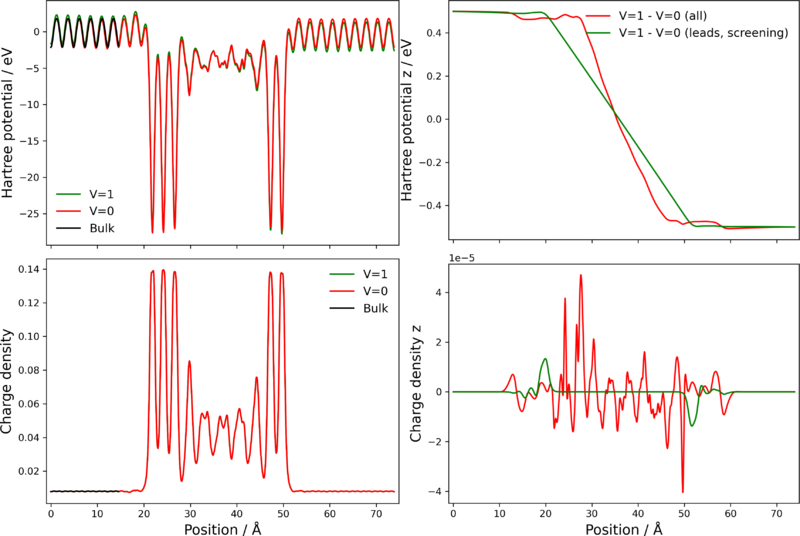
Figure 10 shows the difference in Hartree potential and charge density between CP2K+SMEAGOL V=1 and V=0 calculations performed on the entire structure and also for the structure with the extended molecule removed, including only the leads and screening region.

Figure 10. Hartree potential and charge density (left), Hartree potential and charge density difference (right) between V=1 and V=0 for Au-wire-Au junction calculated CP2K+SMEAGOL.

Performance

Benchmarking

Figure 11. Benchmarking for the Au-BDT-Au junction with varying numbers of basis functions, using SZV-MOLOPT-SR-GTH-q11 for all Au atoms (left) and using a new basis set termed SZV-CUSTOM-q1 for all Au atoms in the leads while using the SZV-MOLOPT-SR-GTH-q11 for all other Au atoms.

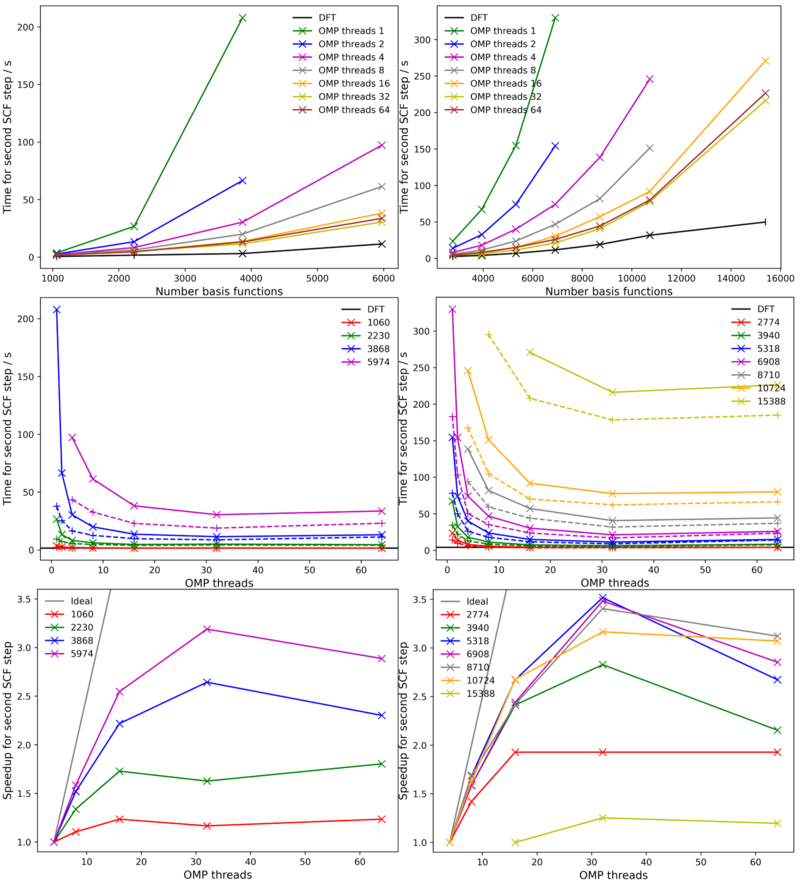
Figure 11 shows benchmark results for an Au-BDT-Au junction with varying numbers of basis functions, which is performed by varying the electrode size. It can be seen that using SZV-MOLOPT-SR-GTH-q11 for all atoms (left) the maximum number of basis functions that CP2K+SMEAGOL can scale up to is around 6000. This is due to the large memory requirements, in particular for the leads where the bulk files 'bulklft.DAT' and 'bulkrgt.DAT' reach 567M for the system with 5974 basis functions. Clearly, reading and distributing such a large file across all MPI processes is very expensive both in terms of CPU time and memory. As such, the time taken for the first SCF step and the memory cost can be decreased by using a smaller basis set for the leads atoms. This is consistent with previous work by the group of Stefano Sanvito, who frequently used a Au basis set with only 6s electrons. Creating a new basis set termed SZV-CUSTOM-q1 and using this for all atoms in the leads decreases the number of basis functions for the leads from 1800 to 200, and decreases the size of the bulk files 'bulklft.DAT' and 'bulkrgt.DAT' from 567M to 9M. With this smaller basis set the system sizes accessible by CP2K+SMEAGOL increases, however the performance for large system sizes remains very poor. Figure 11 shows the speedup per SCF step with increasing number of OMP threads, with a plateau after 32 threads for all system sizes. For the largest system size studied of 15,388 basis functions each SCF step takes over 200s, limiting such system sizes to single point calculations only. For geometry optimisation and in particular for MD, the largest system size that can be calculated using CP2K+SMEAGOL is likely around 10,000 basis functions. The maximum number of OMP threads that can be used to reasonable efficiency is 16, corresponding to a maximum core limit of 1024 with NEnergReal=64 and no kpoint sampling.

In summary, CP2K+SMEAGOL is around 20 times more expensive than CP2K and only relatively small systems or small basis sets can be used. Looking forward to the future of DFT-NEGF calculations, it is likely that an implementation is needed that combines ScaLAPACK with carefully designed highly parallel algorithms.

Profiling

Figure 12. Screenshot of ARM FORGE profile for a single SCF step of CP2K+SMEAGOL for the Au-BDT-Au junction with 3868 basis functions and SZV-MOLOPT-SR-GTH-q11 basis set for all Au atoms.

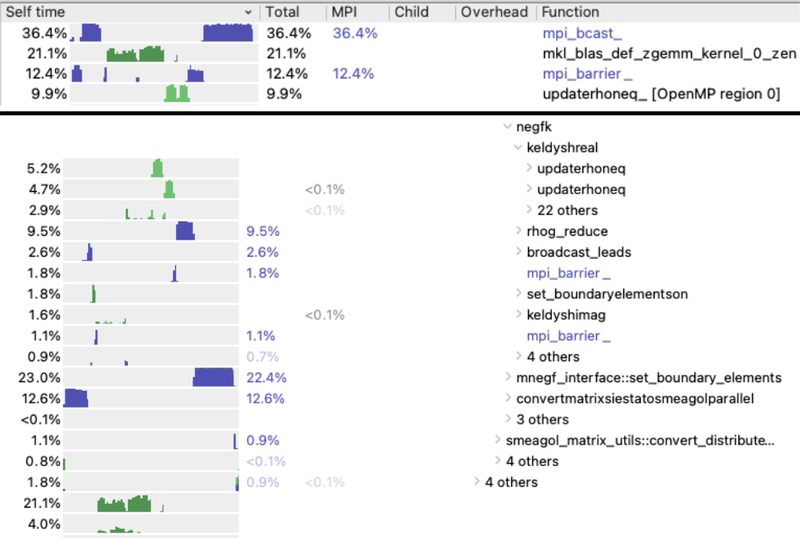
The table below shows the results of profiling the standard version of CP2K+SMEAGOL with ARM FORGE for the Au-BDT-Au system with 3868 basis functions and SZV-MOLOPT-SR-GTH-q11 basis set for all Au atoms. With 1 OMP thread the bottleneck is OMP DO (for loops), and as the number of OMP threads increases the bottleneck becomes serial matrix multiplication matmul() and MPI communication mpi_bcast().

Threads	Time / s	NEGF OMP DO	zgemm()	matmul()	mpi_barrier()	mpi_bcast()
1	1364	40%	28%	7%	6%	5%
2	565	19%	30%	16%	3%	12%
4	335	8%	25%	27%	2%	21%
16	233	3%	9%	39%	5%	27%

The use of serial matrix multiplication in SMEAGOL is clearly inappropriate, and the compiler flag '-external-blas' can be used to automatically convert all matmul() to zgemm(). I have tested the compiler flag '-fblas-matmul-limit' and found that for all matrix sizes relevant for SMEAGOL calculations zgemm() is faster than matmul(). The time taken for 16 OMP threads decreases from 233 s to 146 s, a speedup of 1.6x with only a single compiler flag change. The bottlenecks in SMEAGOL now remain as matrix multiplication and MPI communication, as shown in Figure 12 showing the a screenshot of an ARM FORGE profile zoomed into a single SCF step.

Technical details

Interface design

The current version of the CP2K/SMEAGOL interface is based on the original version of SMEAGOL code linked with SIESTA 1.3f1. Although the SMEAGOL and SIESTA code are tightly coupled, the idea behind the CP2K interface is to reuse the original SMEAGOL code as much as possible. To do so, the original SMEAGOL-related source files became a part of a standalone SMEAGOL library (libsmeagol.a) linkable with alternative Quantum Chemistry software packages. SIESTA-specific parts of the original SMEAGOL Fortran source code were wrapped with preprocessor directives

   #ifndef NOSIESTA

that enables us to compile SMEAGOL core as a library, Instead of implementing CP2K-specific version of the original SIESTA-specific routines of the interface from scratch (which is about 6,000 lines of Fortran code in length) and keep it up to date with ongoing development of SMEAGOL code, we decided to reuse k-point-aware part of the original SIESTA/SMEAGOL interface and to convert CP2K data types into their corresponding SIESTA equivalents instead. The original interface code forms parts of the standalone SMEAGOL library as well.

SMEAGOL-related input keywords

A separate file keywords.txt lists all keywords of the CP2K input section &FORCE EVAL / &DFT / &SMEAGOL alongside relevant components of smeagol control type datatype. Parameters with global scope are passed to SMEAGOL via setting identically-named global variables in SMEAGOL’s negfmod module. These variables are then processed by SMEAGOL core. In contrast, the variables with local scope are processed by the interface itself. For instance, they can be passed to SMEAGOL via subroutines’ arguments, or used to allocate an array defined in global scope of an appropriate size. At the moment, CP2K accepts all input keywords found in the original SIESTA/SMEAGOL interface, even if the corresponding variables are newer accessed.

SIESTA format of sparse matrices

Sparse matrices in SIESTA 1.3f1 are stored in a block-distributed-row compressed-sparse-column format. The blocking factor is defined at compile time via the global parameter BlockSize in SIESTA’s source file parallel.f which is usually equal to 8. There are a number of subroutines to convert between global and local row indices, as well as to query the MPI rank of a parallel process local to a particular global row index. In contrast with ScaLAPACK matrices which use block-cyclic distribution scheme, all non-zero matrix elements on any single row are stored on one MPI process. In fact, SMEAGOL does not rely on a ScaLAPACK library at all. Non-zero matrix elements local to the particular MPI process are stored in a compressed one-dimensional array. Cell images are ordered according to canonical enumeration of integers 0, 1, −1, . . . , n, −n, . . . in x,y,z order, where x is the fastest index.

A list of all internal SIESTA and CP2K variables can be found here, compiled by Sergey. The mentioned CP2K variables form part of the derived siesta distrib csc struct type datatype.

Acknowledgements

This work was supported by the Engineering and Physical Sciences Research Council (grant EP/P033555/1) and developed within Clotilde Cucinotta's group at Imperial College London.

I would like acknowledge specifically the contributions of all authors to this work:

Christian S. Ahart, Imperial College London. I helped finalise the CP2K+SMEAGOL interface, performing extensive benchmarking and validation. I also made some contributions to the CP2K+SMEAGOL interface as well as the SMEAGOL code.

Sergey Chulkov, University of Lincoln. Sergey wrote the CP2K+SMEAGOL interface and developed SMEAGOL into a standalone library.

Clotilde S. Cucinotta, Imperial College London. Clotilde conceived CP2K+SMEAGOL and supervised Christian S. Ahart.

I would also like to thank the following for their helpful discussions:

Stefano Sanvito, Trinity College Dublin. SMEAGOL was developed by the group of Stefano Sanvito at Trinity College Dublin.

Ivan Rungger, National Physical Laboratory. Ivan is one of the original SMEAGOL developers and provided us with helpful insights during the validation state of the CP2K+SMEAGOL development.

Alexandre Reily Rocha, UNESP. Alex is one of the original SMEAGOL developers and provided us with helpful insights during the validation state of the CP2K+SMEAGOL development.

References

<References>