Pk1615
Molecular reaction dynamics
Exercise 1: H + H2 system
Q. What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.
A. The gradient is zero at the potential energy surface minimum and at the transition structure which is the potential energy surface maximum. If one starts a trajectory exactly at the minimum and maximum points with no momentum there will be no change and the trajectory will remain stationary at that position. Whereas in the case of a potential energy surface minima as small change in geometry towards the reactants or products will lead to a small increase in potential energy towards the reactants or products followed by a decrease back to the minimum point as this curve is a well. In the case of a transition state, and energy maximum, a change in geometry towards the reactants or products will lead a decrease in energy towards the direction of change that will be continuous as the point will roll down the curve. To distinguish between them; the second derivative of both the maximum and minimum points can be calculated and should give a value of <0 and >0 respectively.
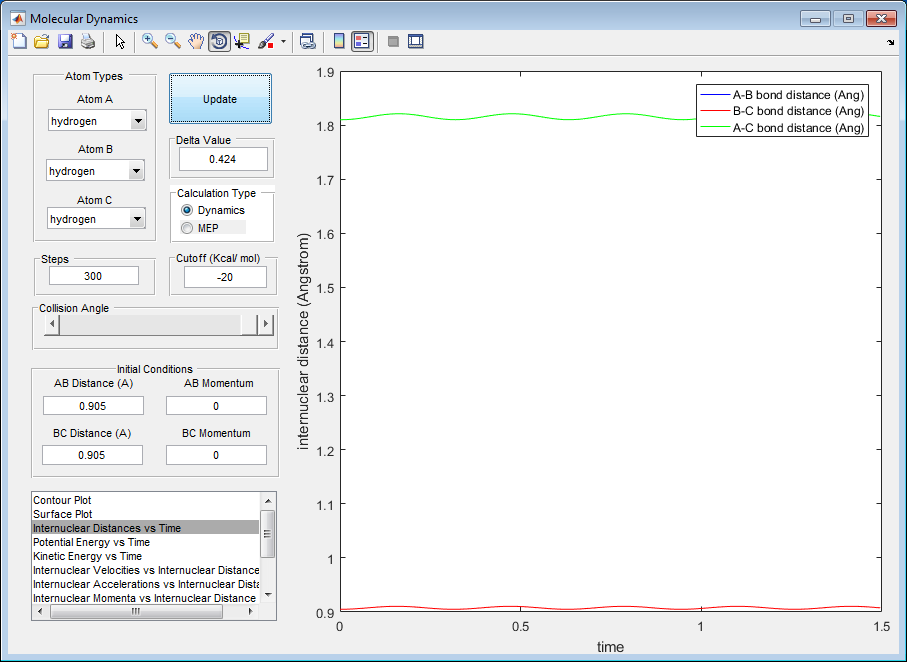
(Fv611 (talk) 15:19, 17 May 2017 (BST) Good. Could have mentioned saddle points) Q. Trajectories from r1 = r2: locating the transition state. Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.
A. Using a surface plot and identifying the point where potential energy vs internuclear position curve maximum and minimum points intersect:
r(ts) is 0.905 Å when r1=r2=1.5 Å r(ts) is 0.905 Å when r1=r2=2.3 Å r(ts) = 0.905 Å
Figure 1
As seen in the figure 1 above the internuclear distance is constant and does not oscillate anymore at the transition state distance. This constant internuclear distance between all bonds is a property of the transition state.
(Fv611 (talk) 15:19, 17 May 2017 (BST) Good, but not sure what you mean by "identifying the point where potential E and internuclear position curve maximum and minimum points intersect". Generally, if you discuss a plot it is better to show it) Q. Calculating the reaction path. Trajectories from r1 = rts+δ, r2 = rts. Comment on how the mep and the trajectory you just calculated differ.
A. In mep the masses of atoms are not taken into account whereas when the dynamics calculation type is run the masses of the atoms are taken into account. This displays a more wavy reaction path line in antithesis to the mep smooth and straighter reaction path line.
(Fv611 (talk) 15:19, 17 May 2017 (BST) The difference is in the treatment of velocity, not that of masses.) Q. Reactive and unreactive trajectories initial positions r1 = 0.74 and r2 = 2.0
| p1 | p2 | result | image |
|---|---|---|---|
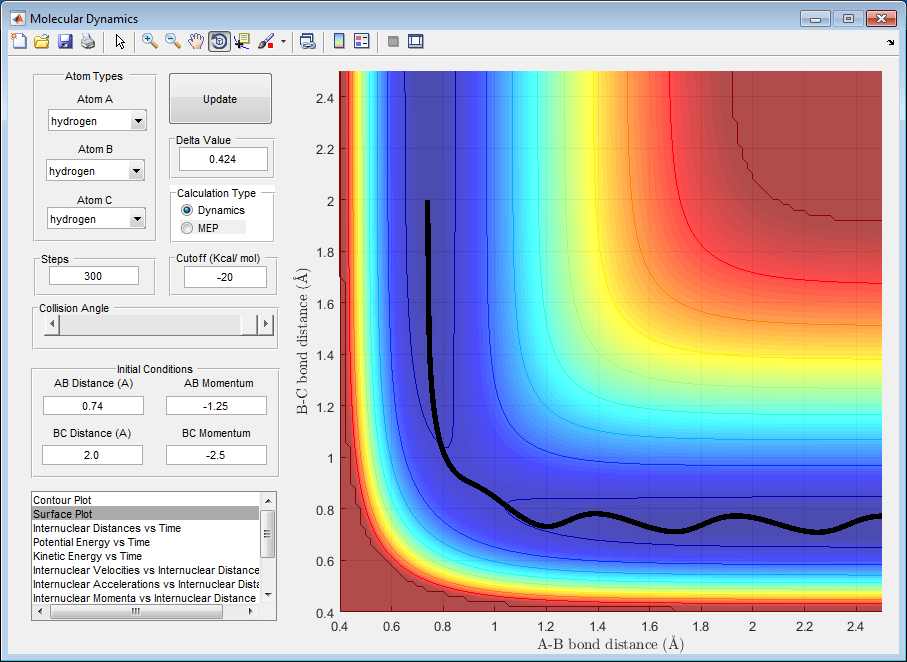
| -1.25 | -2.5 | reactive | figure 2 |
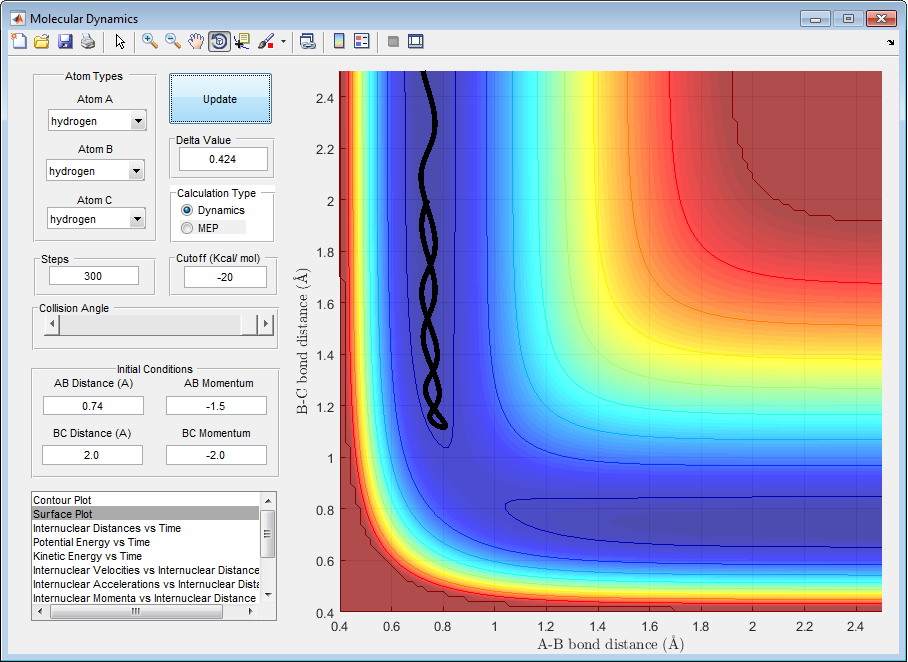
| -1.5 | -2.0 | unreactive | figure 3 |
| -1.5 | -2.5 | reactive | figure 4 |
| -2.5 | -5.0 | unreactive | figure 5 |
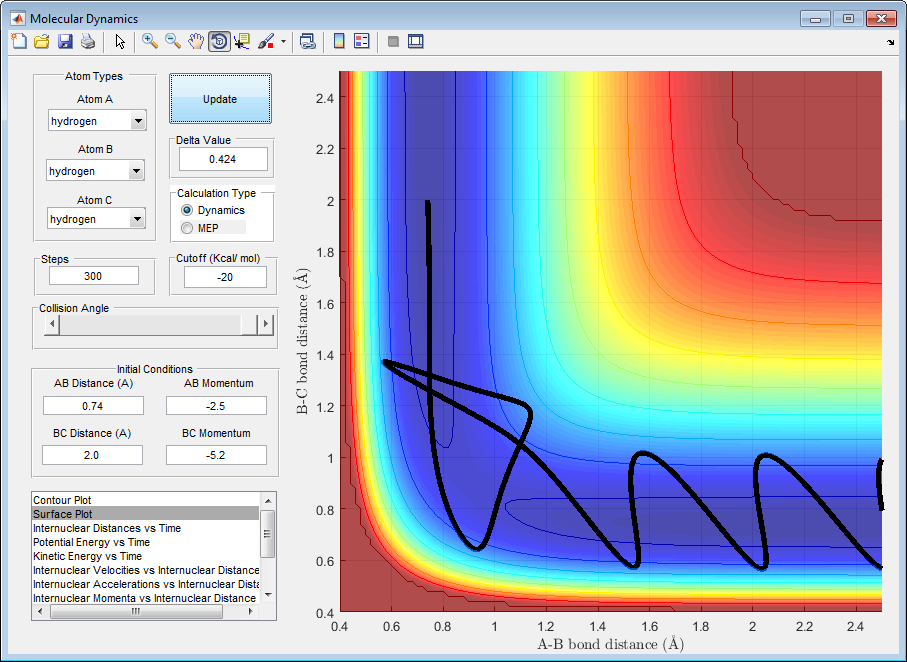
| -2.5 | -5.2 | reactive | figure 6 |
Figure 2
Here it can be seen that the trajectory is reactive because the reaction proceeds from the starting point towards the transition state, as Hc approaches the Ha-Hb molecule, and ends at the products where a Hb-Hc molecule forms with a Ha atom standing alone. This shows that the Ha-Hb distance inreases, the bond is broken between them, as the Hb-Hc distance decreases as a bond is formed between the two atoms.
Figure 3
In figure 3 it can be seen the Hc does not approach the hydrogen molecule with enough momentum to overcome the energy barrier in the reaction, leading to Hc approaching the transition state but the reaction not proceeding to the products as the activation energy was not overcome. The reaction falls back to the reactants. Giving a large BC distance and the Hb and Hc atoms do not form a bond and are found at a distance from each other.
Figure 4
A smooth reaction is seen here, where the Hc approaches the hydrogen molecule with enough energy. At the transition state the energy barrier is overcome and the reaction is driven towards products. Creating the Hb-Hc molecule.
Figure 5
In figure 5 it can be seen that the reaction reaches the transition state and momentarily proceeds towards the products but does not have sufficient energy to continue on the pathway towards the products and is driven towards the reactants again. This trajectory is unreactive. This could be due to lack of momentum needed to reach the products in the reaction.
Figure 6
In figure 6 the molecules react and have sufficient energy to overcome the activation energy barrier at the transition state. Once the transition state has been achieved the molecules are driven up towards the reactants where they then fall back down towards the products, completing the reaction. This trajectory is overall reactive leading to the formation of the Hb-Hc molecule.
(Fv611 (talk) 15:19, 17 May 2017 (BST) Correct, but you make no difference between cases 2 and 4. Also you state that the reactants in case 4 do not have enough energy, even though their energy is higher than in case 1.)
Q. State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
A.Transition state theory classically states that atoms and molecules will react when they approach each other with sufficient energy to overcome the activation energy barrier. When their energy is greater than the activation energy the reaction proceeds to products via the transition state. Based on experimental values the transition state theory values are low since they do not take into account the quantum mechanics of reaction pathways. Atoms and molecules classically may not have enough energy to overcome the activation energy barrier, they can however tunnel through the barrier in this case which does lead to a reaction quantum mechanically. Additionally, it is known that the transition state is located on the saddle point of the potential energy vs internuclear distance graphs. It is possible that a reaction can proceed to the products not by overcoming the energy barrier at the transition state but by taking another reaction path that involves going around the transition state saddle point. This explains why reactions with insufficient energy can still go to completion as they take different pathway routes that are available. Figure 6 shows that the reactants can take multiple pathways to the products as the transition state point is reached but then reactants fall backwards via another pathway available. Eventually the reactants proceed to products giving a reactive trajectory.
(Fv611 (talk) 15:19, 17 May 2017 (BST) Good discussion) Exercise 2: F - H - H system
Q. Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
A. The reaction between F + H2 is exothermic. More energy is released on making the strong H-F bond (569 Kj/mol) compared to the energy that is taken in to break the H-H bond (435 Kj/mol).
The reaction between H + HF is endothermic since it is energetically less favourable to break the H-F bond and make a H-H bond. In this reaction more energy needs to be taken in on breaking the H-F bond than is released on making the H-H bond. This is because the H-F bond is much stronger than a H-H bond.
(Fv611 (talk) 15:19, 17 May 2017 (BST) Good, but could have related it to the shape of the potential energy surface) Q. Locate the approximate position of the transition state.
A. The transition state point is the point where total energy is stationary because of the absence of a net force. This point is described as:
H-H distance = 0.74 Å H-F distance = 1.815 Å
Q. Report the activation energy for both reactions.
A. For the forward (exothermic) reaction the activation energy is found as: TS energy - reactant energy:(-103.7416) - (-103.9313) = 0.1897 kcal/mol
For the backwards reaction (endothermic) reaction the activation energy is found as: TS energy - reactant energy: (-103.7416) - (-133.6446) = 29.90 kcal/mol
It can be seen that the activation energy for the exothermic reaction is very small and therefore the reaction proceeds spontaneously at room temperature.
(Fv611 (talk) 15:19, 17 May 2017 (BST) Activation energy for the forward reaction is a bit off) Q. Reaction Dynamics. In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
A. The law of conservation of energy states that the total energy in a reaction is conserved. The total reaction energy is the sum of potential and kinetic energy. We know for a fact that the product potential energy is lower than the reactant potential energy in this case. Therefore,following the conservation of energy law the products have higher kinetic energy compared to the reactants. It can be seen in the graph of kinetic energy versus time there is a absolute increase when reactants are turned into products proving the statement above.
This can be experimentally proven using IR techniques since the products that have a large kinetic energy value will oscillate, releasing vibrational energy that is detected in IR analysis. It is expected that a H-H bond vibrational peak in the reactant IR spectrum will disappear when the products are formed and a H-F vibrational peak will appear. Also, this vibrational energy is eventually lost through vibrational relaxation emitting a photon. This can be detected using a photon detector.
(Fv611 (talk) 15:19, 17 May 2017 (BST) Good discussion) Q. Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
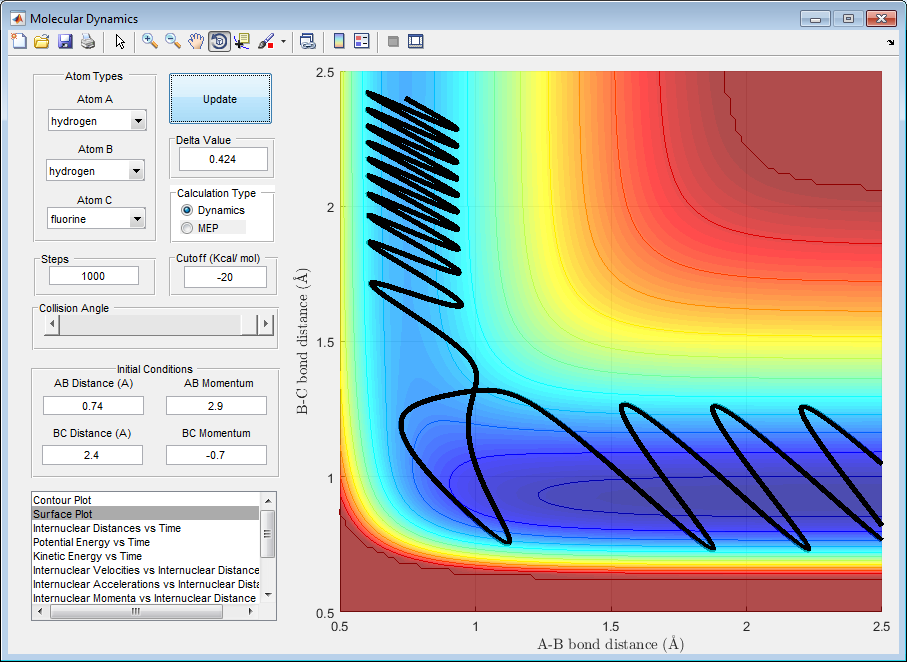
A. In figure 7 it can be seen that for the forward reaction to go to completion an increase in momentum of BC which corresponds to translational energy is required to reach the transition state and overcome it. Any increase in vibrational energy will cause AB to oscillate, it will not have any affect on the reaction, this is wasted energy that makes the reaction less efficient. However, if too much momentum/translational energy is applied then the reaction will not curve towards the products, the reaction pathway will oscillate between very large and small distances of BC.
Figure 7
In the reverse reaction a significant vibrational energy of BC (H-F molecule) is required for the reaction pathway to move towards the reactants and proceed to the transition state. Any increase in momentum of AB would lead to an excess of translational energy and the reaction pathway moving between small and large distances of AB, which is not favourable. This reaction would be less efficient.
The position of the transition state determines what amount of translational and vibtational energy is needed for the reaction to go to completion. If for example the transition state is found more towards one of the reactants or products then more vibrational or translational energy is needed in a specific direction. More momentum needs to be applied in either the reactants or products, as in the case above. If the transition state is found towards the middle of the reaction pathway, the position where the reaction path curves, a good balance of vibrational and translational energy is needed. The position of the transition state therefore determines the amount of momentum that needs to be applied for a reaction to be efficient.
(Fv611 (talk) 15:19, 17 May 2017 (BST) Good. Could have mentioned Polany's rules, but well done in discussing efficiency.)