Parrot on a diet=poly-no-meal

The Hydrogenation of Cyclopentadiene Dimer

Cyclopentadiene can dimerise to form both an endo and exo product; however only the endo dimer is observed. Minimising the geometries using MM2 force field option gives the following data:

Exo Dimer	Endo Dimer
Exo Dimer	Endo Dimer
133.399 kJ/mol	142.271kJ/mol

As we can see, the exo dimer has a lower energy than the endo; this indicates that the exo dimer is the thermodynamically favoured product. However, since only the endo dimer is produced, the reaction is clearly under kinetic contol.

Dihydro Derivative 3

Dihydro Derivative 3

Dihydro Derivative 4

Dihydro Derivative 4

Energy Terms (kJ/mol)	Dihydro Derivative 3	Dihydro Derivative 4
Stretching	5.158	4.588
Bending	78.946	60.713
Van der Waal	17.533	14.487
Hydrogen Bonding	0.683	0.589
Total Energy	150.347	130.348

As can be seen, dihydro derivative 4 has a lower overall energy; looking at individual energy terms, derivative 4 has lower values in all terms except Torsion. Dihydro Derivative 4 is, therefore, the thermodynamic product.

Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)

Pyridinium Reactant 1

pyridinium reactant 1

By viewing the above 3D representation of the Pyridinium Reactant 1, we can clearly see that the carbonyl oxygen sits above the plane of the pyridinium ring. In fact; this dihedral angle is 21.8°.

If, instead, we look at a larger molecule containing a pyridinium ring, we see a similar relationship;

Pyridinium Reactant 2

pyridinium reactant 2

Here, we can see a similar effect, as in the carbonyl oxygen again sits above the plane of the pyridinium ring. Here the dihedral angle is 38.5°.

In both of these cases, the carbonyl oxygen sits above the ring, and we see sterioselective products.

For the example involving the optically active derivative of prolinol (1), the Mg in the MeMgI (which attacks the ring) first coordinates to the O. This means that the Me group is always added stereoselectivly to the top face of the aromatic ring or, more accurately, always adds to the same side of the ring to which the carbonyl group is offset.

For the second example, it is the Hydrogen which coordinates to the carbonyl group (as it has the greatest partial positive charge). Again, we see the stereoselective addition to only the “top” face of the pyridinium ring.

In order to more easily predict the highly stereoselective nature of the addition process, it would be useful to have the dihedral angles shown on the models. This would save the process of computer modelling the molecules, and would then only take some 3D visualisation.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

Taxol intermidiate A

Taxol intermidiate A

Taxol intermidiate B

Taxol intermidiate B

From the MM2 minimisation, the down isomer (B) seems to be the more stable (lower energy). The problem is, when an electrophile comes in to attack the alkene, it will either coordinate to or attack the carbonyl bond.

The alkene carbon-carbon bond itself is hindered in both of these Taxol, the only direction of attack which is not massively sterically hindered is down the direction of the Carbon- Hydrogen bond. Attack from any other angle has a steric clash either with the two methyl groups on the pentane ring, or the bulk of the molecule itself. Therefore the rate of reaction of the alkene C-C double bond will be slow.

In B, since the oxygen is on the opposite face of the molecule, any electrophile will be coming in at the wrong angle to attack the alkene (opposite to the C-H bond). Since this appears to be the more favoured isomer, then the rate of reaction of the alkene will be slower than expected.

In A, the carbonyl group has direction which is more beneficial for the reaction of the alkene C-C double bond, i.e. the oxygen of the carbonyl is pointing in the same direction as the C-H bond. This means that a coordinating electrophile will be in the correct position to attack the alkene C-C double bond.

How one might induce room temperature hydrolysis of a peptide

N-(2-hydroxyethyl)glycine amide 1 (Axial conformation)	N-(2-hydroxyethyl)glycine amide 1 (Equatorial conformation)
Axial Conformation	Equatorial Conformation

N-(2-hydroxyethyl)glycine amide 2 (Axial conformation)	N-(2-hydroxyethyl)glycine amide 2 (Equatorial conformation)
Axial Conformation	Equatorial Conformation

Here, we are looking for attack from the oxygen in the OH group, to the carbonyl carbon, which will “kick off” the bonded NH2. For this to happen, the carbonyl carbon has to be able to rotate into a position where it is not only in the correct geometric coordinates for the nucleophilic attack to occur, but also approaching at the right angle. However, because we have free rotation around the OH group (and therefore its lone pairs), the angle of attack does not really come into calculations. The only angles of attack which would be inappropriate would have large steric clash, as they would have to pass near to the bulk of the molecule.

Starting with N-(2-hydroxyethyl)glycine amide 1, with the N-substituted group in the equatorial position, it is clear that, after manipulation, the carbonyl carbon is in an ideal position for attack from the lone pair on the oxygen of the OH group. After rotation, the carbon sits almost exactly between the Oxygen and the Nitrogen bonded carbon.

Looking at the axial conformation and both the axial and equatorial conformations for N-(2-hydroxyethyl)glycine amide 2 ; it does not matter which angle the carbonyl carbon is rotated around the nitrogen bonded carbon; none of these come into a desirable distance to the OH group for easy attack by the oxygen lone pair.

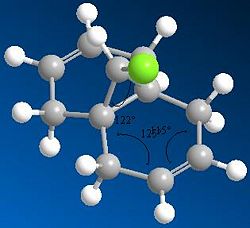
Regioselective Addition of chlorodicarbene

MM2 Minimisation

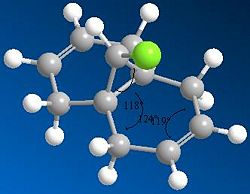
As can be seen in the MM2 approximation;

The angle between the Chlorine and the first carbon of the ring is approximately 118°

The angle between the first two C-C bonds of the ring is 119°

The angle between the C-C double bond and the bonded carbons is 124°

HF/STO-3G Minimisation

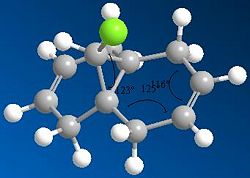
Using the HF/STO-3G self-consistent-field MO method we see a different set of equilibrium angles come out.

Here the angle between the Chlorine and the first carbon of the ring is approximately 122°

the angle between the first two C-C bonds of the ring is 115°

the angle between the C-C double bond and the bonded carbons is 125°

DFT Minimisation

Finally, after analysis utilising the SCAN function on the network, we can analyse the molecule by quantum mechanical modelling using Density Functional theory. In this case we see another set of favoured angles come out of the calculations:

Now we see the angle between the Chlorine and the first carbon of the ring is approximately 123°

The angle between the first two C-C bonds of the ring is 116°

The angle between the C-C double bond and the bonded carbons is 125°

There is not that much difference between the values given by the HF/STO-3G self-consistent-field MO method and by quantum mechanical modelling using Density Functional theory, however their running times are very different. The DFT method utilises functionals (functions of functions) of electron density to calculate the most favoured configuration. This process requires more processing power than the HF/STO-3G method (which looks at the molecular orbitals) and it also requires more time.

One would assume that the calculation which takes longer to run would be the more valuable, but ignoring that and thinking logically; the approximation which takes into account electron density should be more accurate than an approximation which only considers the generalised probable location of electrons.

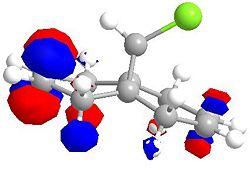
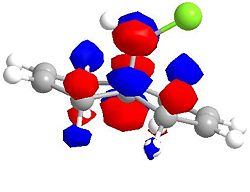
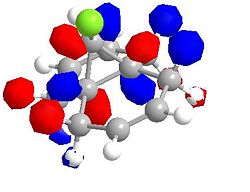
Molecular Orbitals for Chlorodicarbene

HOMO -1	HOMO
HOMO -1	HOMO

LUMO	LUMO +1
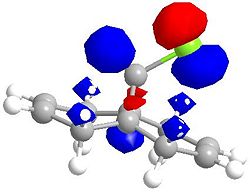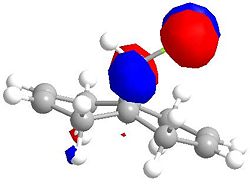LUMO	LUMO +1

LUMO +2	LUMO +2 (second angle)
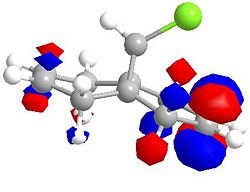LUMO +2	LUMO +2 (second angle)

Identifying Stretching Vibrations

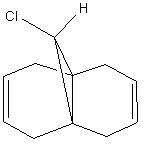
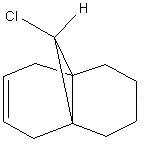
Chlorodicarbene	Chloromonocarbene

The HF/STO-3G minimised molecules were inputted into a DFT minimising program; this allowed for the identification of the major stretching frequencies for the C-Cl bond and the C=C bonds.

	Chlorodicarbene	Chloromonocarbene
C-Cl stretching frequencies (Hz)	903.6	930.3
C=C stretching Frequencies (Hz)	1740.8 (anti) & 1761.0 (syn)	1761.7

It is clear that the stretching frequencies have not changed by a large amount, as expected. It is seen that the C-Cl stretching frequency has changed more than the C=C stretching frequency. This is to be expected as the C-Cl bond is no longer interacting with the C=C which was anti to it. the C=C bond has not changed much, as it was not near to (or able to be largly acted upon by) the second C=C.

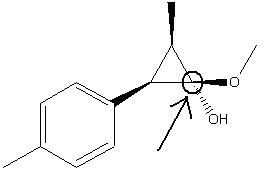
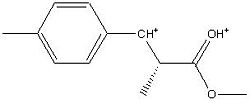
Mini Project; the Analysis of the 1-(4’-Methylphenyl)-2-methoxycarbonyl-propan-1-carbenium ion

1-(4’-Methylphenyl)-2-methoxycarbonyl-propan-1-carbenium ion

1-(4’-Methylphenyl)-2-methoxycarbonyl-propan-1-carbenium ion

Axial Conformation

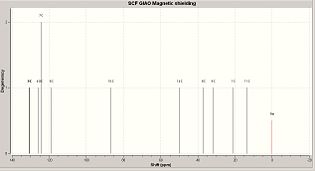
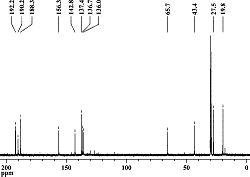
After selecting a molecule, the 1-(4’-Methylphenyl)-2-methoxycarbonyl-propan-1-carbenium ion was inputted into ChemBio 3D for basic minimisation (MM2). Upon completion, the molecule was submitted to the SCAN servers for DFT (Density Functional Theory) analysis.

The (now minimised) 1-(4’-Methylphenyl)-2-methoxycarbonyl-propan-1-carbenium ion was then re-submitted to SCAN for NMR analysis, so that a comparison could be made between the calculated C13 NMR spectrum, and the Literature C13 Spectrum.

However, upon comparison, an annomaly was detected:

Calculated NMR	Literature NMR
Callculated C13 NMR	Callculated C13 NMR
Peaks form Calculated NMR (Hz)	Peaks form Literature NMR (Hz)
13.4
20.9	19.8
31.7	27.5
36.9
49.7	43.4
	65.7
86.7
118.7
124.4	136.0
124.4	136.7
125.7	137.4
	142.9
	156.3
	188.3
130.5	190.2
130.6	192.1

(Data grouped to compare similar values, showing where the obtained frequencies are similar

(similar chemical environments) and where the obtained frequencies are disimilar (different

chemical environments))

It is clear that the spectra are not of the same molecule, although they share a number of similar peaks, there are others that are clearly not related.

Analysis of DFT Minimised Molecule

At this point, the origonally minimised Molecule was loaded into GaussView for inspection; and an interesting anomally was found:

Axial Conformation

It is clear that, in the process of the DFT minimisation, a propane ring has been formed. After re-running all the minimisations, and replicating the results, this was found to not be simple human error. At first glance, it seemed that the software had malfunctioned and failed and had apparently performed this conversion:

Conversion

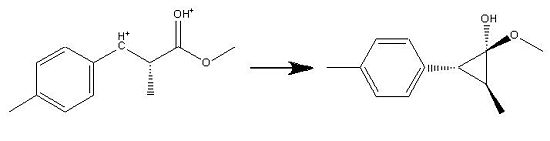
it appeared that the software had not taken into account the charges on the ion and had introduced an H^- ion, thereby performing this unfavoured arrow pushing;

Conversion

However, upon closer inspection of the method and the molecule, it was determined that somthing more interesting had happened and this rather clever arrow pushing had instead occured;

Conversion

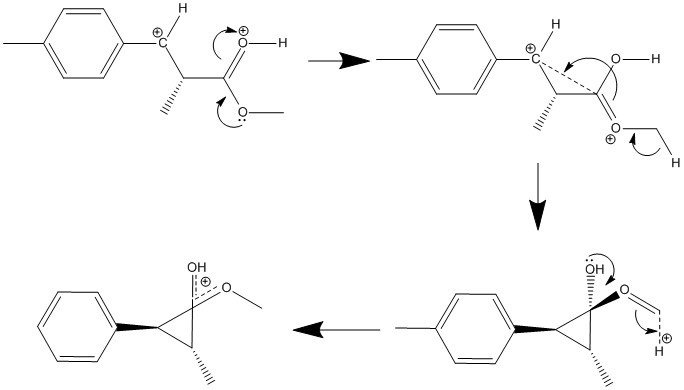
The DFT minimisation software had determined that a delocalised positive charge between the two oxygen groups is more favoured than the previous ion, as shown here;

Axial Conformation

Therefore the minimised molecule (affectionately called “BOB”) is the thermodynamically favoured conformation, where as the literature conformation would be the kinetic product. Looking at reaction conditions, the molecule was kept at extremely low temperatures (-70 to -78°C). This presumably means that the molecule was unable to take its energetically more favourable conformation as it was unable to overcome the energy barrier for this conversion.

Predicting ³J H-H couplings

It is possible to, fairly accuratly, "guess" the ³J H-H couplings of a molecule by looking at the dihedral angles, and compareing these values to a Karplus curve. To do this, the molecule (BOB) was inputted into a JAVA program by the name of Janocchio. Using this, the following ³J H-H couplings were found:

Conversion

3J (H1–H2) coupling	3J (H2–H3) coupling	3J (H4–H5) coupling
13.0 Hz/3.1 Hz/3.3 Hz
6.5 Hz	9.1 Hz	8.2 Hz

• the frequencies were averaged for the case of the methyl group

Predicting the IR Spectrum

The minimised molecule (BOB) was submitted to the SCAN servers again, but this time to predict its molecular vibrations:

C-O (OH) bending frequency	307.3 Hz	vibration at 307
C-O (ether) bending frequency	460.5 Hz	vibration at 460

C-O (ether) stretching frequency	(1225.5 – 8%) Hz	1127.5 Hz	vibration at 1127
C-O (OH) stretching frequency	(1239.5 – 8%) Hz	1140.3 Hz	vibration at 1140
C6 ring asymmetric stretch	(1623.5 – 8%) Hz	1493.6 Hz	vibration at 1493
C6 ring symmetric stretch	(1673.5 – 8%) Hz	1539.6 Hz	vibration at 1539

Predicting the Optical Rotation

BOB was then submitted to the SCAN servers one last time, now to determine the degree of optical rotation.

Chiral Center of the molecule BOB

(showing that the isomer is the S isomer, not the R)

[Alpha]D	57.60°