Organic:Alexandra

Module 1: Organic

The hydrogenation of the cyclopentadiene dimer

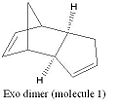
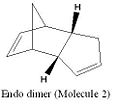
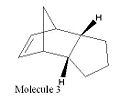
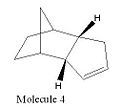
Cyclopentadiene has two dimeric forms; the exo and the endo (molecules 1 and 2 respectively). When dimerisation occurs the endo form of the dimer predominates. If either of the dimeric forms are hydrogenated the dihydro derivatives (molecules 3 and 4) are formed. To investigate the change in energies between the two dimers and their dihydro derivatives the molecules were modelled in ChemBio3D. The molecules were drawn and then their energies optimised using the MM2 force field using molecular modelling theory. Molecular mechanics is a classical method which uses specific force fields to express experimental data as potential functions. There are many different types of force fields, for the purposes of these experiments the MM2 force field will be used. The MM2 force field uses a sum of the following potential functions as the basis for its calculations.

Energy_total = Energy_bonded + Energy_non-bonded

where Energy_non-bonded = Energy_{electrostatics} + Energy_VanderWaals

The main advantages of molecular mechanics theory is that it is a fast method which requires little computational time hence it is a computationally cheap method. However there are several disadvantages with using this theory. The molecules being modelled must maintain connectivity, this obviously presents problems as the method is then only useful for comparing molecules which are structurally very similar. Molecular mechanics theory cannot provide negative energies. The method is parameterised, each different force field type has different parameters set in it, therefore comparisons cannot be made of values calculated from different force fields. The method is also not ab initio.

From the MM2 calculations the total energy of the exo dimer was found to be 133.39kJmol^-1 and the endo dimer was 156.67kJmol^-1. From this it can be determined that the exo dimer is the thermodynamic product, due to its lower energy making it more stable. Cyclopentadiene is known to dimerise solely to form the endo product suggesting that it is a kinetically controlled and therefore an irreversible process.

Using the same technique, ChemBio3D with the MM2 force field, molecules 3 and 4 were analysed. Molecule 4 was found to be the most thermodynamically stable of the two with a total energy 130.39kJmol^-1. The contributions to total energy of stretching, bending, torsion, Van der Waals forces and hydrogen bonding were all investigated also. Contribution to the total energy of stretching was small for molecule 4 (4.59kJmol^-1) and small, in comparison with the total energy of the molecule, for molecule 3 (9.18kJmol^-1). This implies the bonds in both molecules have not been stretched much longer than their usual lengths. The hydrogen bonding contributions to the total energy are both small 0.7kJmol^-1 for molecule 3 and 0.6kJmol^-1 for molecule 4. The lack of significant hydrogen bonding in either of these molecules is due to the absence of any electronegative atoms, such as O, N etc, between which hydrogen bonds could form. Bending and torsion vibrations make up a significant portion of the total energy for both molecules. The bending energy for molecule 3 is significantly larger than for molecule 4 suggesting the bonds are more bent in molecule 3 reducing their stability. Van der Waals contributions for both molecules are fairly small 28.25kJmol^-1 (molecule 3) and 18.85kJmol^-1 (molecule 4).

'	Molecule 1	Molecule 2	Molecule 3	Molecule 4
Stretch/kJmol^-1	5.39	8.31	9.18	4.59
Bend/kJmol^-1	86.12	90.48	86.50	60.67
Torsion/kJmol^-1	32.09	44.55	53.88	52.37
1,4-VdW/kJmol^-1	17.72	23.68	28.25	18.85
Total Energy/kJmol^-1	133.39	156.66	170.99	130.39

Stereochemistry of nucelophilic additions to a pyridinium ring (NAD⁺ analogue)

In the following reactions both molecule 5 and 7 undergo nucleophilic addition of the pyridine rings within their structure. In both cases the molecules both have carbonyl groups which affect the way nucelophilic addition occurs. To determine just how these groups affect nucleophiles attacking the pyridine rings within the molecules, the molecules were both modelled on ChemBio3D and the energies minimised using the MM2 force field. When using MM2 to optimise the geometry of the molecules it was found that the preferred orientation of the carbonyl bond was out of the plane of the molecule. The reagent for the conversion of molecule 5 to 6 is MeMgI, this grignard reagent could not be modelled using chemdraw as the Mg atom is not recognised by the program. To get a higher energy conformation of molecule 5 it was necessary to manipulate the dihedral angle between the C=O bond and the H where methylation occurs on the pyridinium ring. Below is the data from manipulation of the dihedral angle.

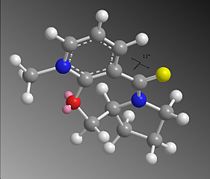
Molecule 5 with dihedral angle 11 degrees

Stretch:                8.65 kJ/mol
Bend:                   60.17  kJ/mol
Stretch-Bend:           0.66   kJ/mol
Torsion:                25.24  kJ/mol
Non-1,4 VDW:            -1.95  kJ/mol
1,4 VDW:                69.98 kJ/mol
Charge/Dipole:          40.56   kJ/mol
Dipole/Dipole:         -16.57  kJ/mol
Total Energy:           186.73 kJ/mol

Molecule 5 with dihedral angle -122 degrees

Stretch:                15.88   kJ/mol
Bend:                   469.68  kJ/mol
Stretch-Bend:          -1.21    kJ/mol
Torsion:                124.40  kJ/mol
Non-1,4 VDW:           -34.61   kJ/mol
1,4 VDW:                69.98   kJ/mol
Charge/Dipole:         -34.61   kJ/mol
Dipole/Dipole:         -14.61   kJ/mol
Total Energy:           681.06  kJ/mol

The change in dihedral angle of the carbonyl group and the ring, from 11 degrees to -112 degrees, results in a far higher energy conformation of the molecule. This occurs because when the molecule is being modelled using MM2 it will try to return to its lowest energy conformer. To model the molecule with a high energy conformer it was necessary to distort many of the bonds in the molecule, particularly those bonds in the five membered ring. 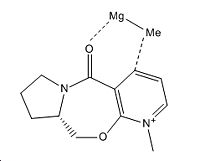In the product of the methylation of molecule 5 the methyl group is orientated out from the ring with absolute stereochemistry. To explain the absolute stereochemistry of this reaction it is necessary to look at the reaction intermediate. When the magnesium species comes in to attack the ring, the Mg atom coordinates with the oxygen of the carbonyl group therefore the methyl group adds to the ring on the same face as the magnesium.

Molecule 7 with dihedral angle -20 degrees

Stretch:                15.42  kJ/mol
Bend:                   48.51  kJ/mol
Stretch-Bend:           1.68   kJ/mol
Torsion:                42.46  kJ/mol
Non-1,4 VDW:            14.52  kJ/mol
1,4 VDW:                123.29 kJ/mol
Charge/Dipole:          8.03   kJ/mol
Dipole/Dipole:         -20.41  kJ/mol
Total Energy:           233.48 kJ/mol

Once again the dihedral angle was changed to try and find a higher energy conformation of molecule 7:

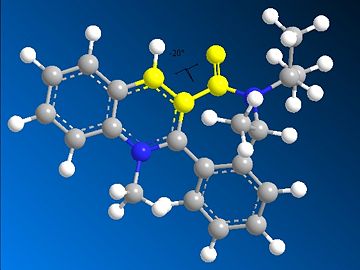
Molecule 7 with dihedral angle 125 degrees

Stretch:                87.87   kJ/mol
Bend:                   528.76  kJ/mol
Stretch-Bend:          -13.16   kJ/mol
Torsion:                133.09  kJ/mol
Non-1,4 VDW:            55.25   kJ/mol
1,4 VDW:                202.44  kJ/mol
Charge/Dipole:         -5.53    kJ/mol
Dipole/Dipole:         -22.50   kJ/mol
Total Energy:           966.23  kJ/mol

As with molecule 5 the change in dihedral angle, between the plane of the ring and the carbonyl group, results in a large change in total energy of the molecule. The mechanism of the attack of PhNH₂ is different to the attack of the Grignard in the mechanism before. Where the Grignard reagent was capable of coordinating to the oxygen of the carbonyl group, the PhNH₂ group is not. The Mg of the Grignard reagent was small and electropositive enough to coordinate to the oxygen whereas the N atom is not small enough or electropositive enough. Also the N based reagent is quite sterically hindered which will also prevent coordination to the oxygen atom. Despite this the reaction still takes place with absolute stereochemistry. The cause of the absolute stereochemistry of the reaction is sterics. If the N based reagent attacks the pyridine ring from the top face of the ring, there will be considerably less steric hinderence from the carbonyl group ¹. Also both oxygen and nitrogen are highly electronegative atoms with lone electron pairs. If they come within close proximity of each other there will be electron-electron repulsions between the lone pairs, resulting in a destabilisation of the molecule. For these two reasons the N reagent will always attack from the top face of the molecule ². A. G. Shultz, L. Flood and J. P. Springer, J. Org. Chemistry, 1986, 51, 838. DOI:10.1021/jo00356a016 Leleu, Stephane; Papamicael, Cyril; Marsais, Francis; Dupas, Georges; Levacher, Vincent. Tetrahedron: Asymmetry, 2004, 15, 3919-3928. DOI:10.1016/j.tetasy.2004.11.004

Stereochemistry and reactivity of an intermediate in the synthesis of Taxol

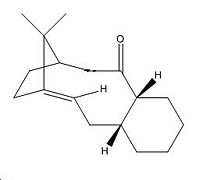
Molecule 9 is an intermediate in the synthesis of the ovarian cancer drug Taxol, it is also a good example of atropisomerism, as the molecule will isomerise to the least energetic conformation. To determine which isomer of the molecule is most favourable the two different isomers, one with carbonyl bond facing up and one with it facing down, the two molecules was modelled on ChemBio 3D and using the MM2 force field their energies optimised. From this it was found that the two isomers correspond to the 6 membered ring being in either the chair conformation, carbonyl group facing down, or the twist boat conformation, carbonyl group facing up.

From the energy optimisation it was found that the chair conformation was the lower energy isomer with a total energy of 185.26kJ/mol. To get the twist boat conformer it was necessary to manually manipulate the bonds in the molecule, from this the total energy was found to be 250.94kJ/mol. As the chair conformation is lower in energy it is the most stable isomer, and the isomer that the molecule always returns to.

It has been found that the alkene bond in the molecule reacts incredibly slowly. Molecule 9 is in a class of molecules known as hyperstable alkenes. Hyperstable alkenes are such because of the positioning of the alkene bond at the bridgehead. The positioning of the alkene bond here stabilises the molecule. ¹

Hydrogenation of this bond destabilises the molecule, by raising the strain energy of the molecule. This occurs because the deforming of the C=C when reacting as the C atoms go from sp2 hybridisation to sp3 hybridisation. In the molecule this leads to a raising in energy of the HOMO and a lowering in energy of the LUMO, this overall raise in energy is unfavourable hence the reluctance of the alkene to react. ²

1. Wilhelm F. Maier and Paul von Rague Schleyer, J. Am. Chemical Soc, 1981,103, 1891-1900 DOI:10.1021/ja00398a003

2. Camps. P, Perez. F, Vazquez. S, Tetrahedron, 1997, 53, 28, 9727-9734

Modelling using semi-empirical Molecular Orbital Theory

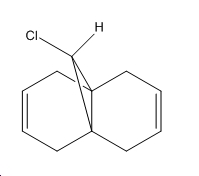
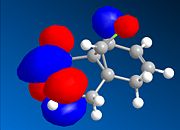
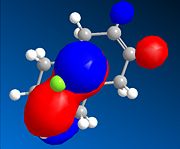
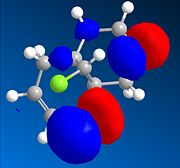
The dialkene, Molecule 12, is a simple molecule to investigate the control molecular orbitals have upon reactivity. The MM2 force field was initally used to optimise the geometry of the molecule before applying MOPAC/PM6 methods to model the molecular orbitals of the molecule. PM6 is a semi-empirical calculation used for calculating molecular eletronic structure. Semi-empirical methods are based on the Hartree-Fock approximation. However as the full Hartree-Fock approximation is computationally expensive, semi-empirical methods have some empirically derivied parameterised approximations. ChemBio3D was used to do the calculations associated with these electronic methods. The HOMO-1, HOMO, LUMO, LUMO+1 and LUMO+2 were used to analyse the molecule.

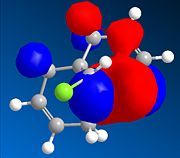From the calculation of the molecular orbitals it is apparent that the HOMO lies mainly on the alkene bond endo to the chloro substituent on the cyclopropane ring, the highest energy electrons lie in the HOMO and therefore are most likely to undergo electrophilic attack. It is, therefore, the alkene bond endo to the chloro substituent which will undergo electrophilic attack. The explanation suggested for this regioselectivity is '...stabilising antiperiplanar interactions between the CI-C o* orbital and the occupied exo π-orbital, rendering the endo double bond more nucleophilic in both a frontier orbital and an electrostatic sense.¹

Using the PM6 optimised molecule 12 and a partially hydrogenated version of molecule 12, also PM6 optimised, Gaussian was used to calculate the various bond vibrational frequencies within the molecule. The Gausssian file was run using '# b3lyp/6-31G(d,p) opt freq'. GAUSSIAN uses gaussian functions to model atomic orbitals, to be used in LCAO method. There are many different types of calculations which can be done using GAUSSIAN software. In these calculations density functional theory was used, DFT uses functions of functions to determine proeprties of a many electron system. It is a computationally cheap method and has a good correlation with experiment values, for these reasons it is a good theory to use to model the diene and monoene. The basis set that was used in these calculation was the 6-31G(d,p) basis set. In this basis set 6 gaussians are used to model the core electrons, 3+1 gaussians are used for outer/valenece electrons. The 6-31G(d,p) basis set adds d orbitals to second row elements. The advantages of this is that it allows the modelled orbitals of these elements to be less directional and more flexible. This feature is particularly useful in anions where there is a high level of electron density. 6-31G(d,p) also adds p orbitals to H atoms. A good way to make the calculations more accurate would be to not use gaussian functions to approximate the electron wavefunction integrals, as in comparison to other available approximations gaussians do not have a high level of accuracy. However as GAUSSIAN software is based on gaussian functions, it finds electron integrals easier to solve analytically than it would other more accurate functional approximations. Once the calculations had been completed the formatted checkpoint file was used to determine the vibrational frequencies of the C=C and C-Cl bonds.

Bond Type	Monoene/cm-¹	Dialkene/cm-¹
C=C	1758.06	1757.36
C=C	n/a	1737.09
C-Cl	774.96	770.90

From simple harmonic motion it is known that the bond frequency, $ν = (\frac{1}{2 Π}) \sqrt{\frac{k}{μ}}$

where k=force constant and μ=effective mass. The force constant is determined by the strength of a bond, therefore if a bond is strong it will lead to a higher frequency of vibration. The C=C in the dialkene which is not represented in the monoalkene is that of bond anti to the Cl atom. In the dialkene the C=C exo to the chlorine atom has a slightly lower stretching frequency than the other C=C. The carbon-chlorine σ* orbital is capable of donating electron density into the C=C bond anti to the chlorine atom. The effect of this energy donation is a weakening of the π-bond reducing its strength and therefore lowering its stretching vibrational frequency. Below is a jmol of both the diene and monoene.

||

1. B. Halton, R. Boese and H. S. Rzepa., J. Chem. Soc., Perkin Trans 2, 1992, 447. DOI:10.1039/P29920000447

Structure based Mini project using DFT-based Molecular orbital methods

In 2001 T. Johnson and E. J. Corey attempted to synthesise the compound, which at the time was thought to be the structure, psuedopteroxazole. The structure was to be determined through total synthesis. The second step of the outlined scheme was a diastereoselective intramolecular Diels-Alder leading to the diastereoisomers 1 and 2.

The endo product 1 is formed in a 69% yield with a small proportion of the diastereomeric adduct 2, in an 8:1 ratio. The selectivity of the endo product over exo product is explained through the transition state of the Diels-Alder reaction. It was reported that the major isomer '...showed a large coupling between the protons α and β to the lactam carbonyl and the diastereomeric minor cycloadduct which displayed only a small coupling between the protons α and β to the lactam carbonyl.'¹

To attempt to determine the reasoning behind the endo product being the major isomer formed, the energies of both of the molecules were calculated. As in previous calculations ChemBio3D with molecular mechanics theory and the MM2 force field was used. The endo product was found to have an energy of 17.76kJ/mol and the exo product was found to have an energy of 16.39kJ/mol. From this calculation the two molecules have a ΔG=1.37kJ/mol.

This is interesting as despite the exo product being of a lower energy it is not the main product. In the Diels-Alder reaction the transition state determines whether it is the endo or exo product that predominates. In the case of this particular reaction it was found that in the transition state leading to the exo product there is significant steric hinderence between the the methyl substituent on the α-carbon and the olefinic hydrogen which resulted in a higher energy transition state.¹ Hence the endo product predominates, the proportion of the product formed as the exo diastereoisomer is most likely due to the exo product being the thermodynamically favoured product.

1.Johnson. T, Corey. E J, J. Am. Chem. Soc. 2001, 123, 4475-4479

Calculating coupling between the protons α and β to the lactam carbonyl

The two diastereoisomers were drawn on ChemBioUltra3D, their energies were then minimised using the MM2 force field and their geometries optimised using GAUSSIAN. The DFT method used was MPW1PW91, this particular method has been found to be better at NMR calculations than the more often used B3LYP. The basis set used for the calculations is the 6-31G(d,p). After the geometries of the molecules had been optimised the molecules had their NMR chemical shifts calculated in chloroform solvent. The chemical shifts calculated are below. From the calculation of the optimum geometry of both of the molecules structure, it was possible to calculate the angle between the two hydrogens α and β to the lactam carbonyl and therefore use the Karplus equation to calculate their coupling constant.

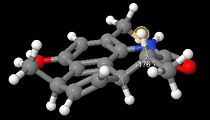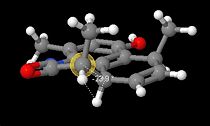Using Janocchio ([1]) the angle between the two hydrogens α and β to the lactam carbonyl was calculated and the coupling constants were also calculated. It was found that for the Major isomer (compound 1) θ =-176.7 and for the minor isomer (compound 2) θ=-23.9.

Diastereisomer	Predicted J/Hz	Experimentally determined J/Hz
Major isomer	11.2	14.0
Minor isomer	5.7	5.0

Although there is a slight discrepency between the reported values and the predicted ones, there is still a significant difference between the coupling constants calculated for each diastereoisomer and therefore this method can still be used to discriminate between the two isomers.

NMR predictions for the diastereoisomers

GAUSSIAN was used to predict the NMR for both compounds. The prediction was done using the MPW1PW91 DFT method, and the 631G(d,p) basis set.

Major Isomer:

The following ¹H and ¹³C nmr were determined using the previous method, CDCl₃ was the solvent with which the NMR predictions were determined.

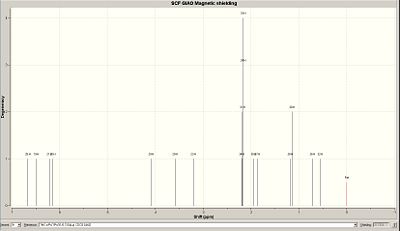Using the journal in which the compounds were reported it was possible to match up the predicted NMR values of selective protons and the experimental values.

Proton	Predicted Chemical Shift/ppm	Experimental Chemical Shift/ppm
N-H	6.67	7.44
O-H	4.09	5.19
β-H (β to carbonyl group)	3.20	3.18
α-H (α to carbonyl group)	2.16	2.29

Carbon atom	Predicted Chemical Shift/ppm	Experimental Chemical Shift/ppm
C=O	166.0	147.11
C-OH	144.34	148.84
C with β-H	41.24	40.67
C with α-H	39.98	37.43

There is a fairly good correlation between predicted values of chemical shift and the experimental values for the journal.

Minor Isomer

Using the same method as before the NMR values for the minor isomer were determined.

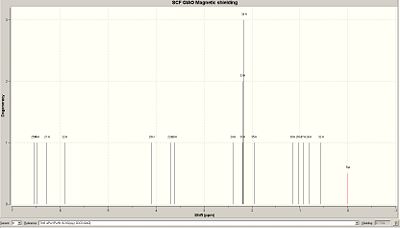Proton	Predicted Chemical Shift/ppm	Experimental Chemical Shift/ppm
N-H	6.54	7.24
O-H	4.09	5.59
β-H (β to carbonyl group)	3.71	3.77
α-H (α to carbonyl group)	2.39	2.77

Carbon atom	Predicted Chemical Shift/ppm
C=O	166.89
C-OH	144.44
C with β-H	41.49
C with α-H	38.83

There were no assignments for ¹³C nmr in the journal, so no comparisons could be made from predicted values and experimental values. There appears to be a correlation between the values which do not correlate well with experimental data and those H/C being attached to heteroatoms. This suggests that the calculations do not handle heteroatoms as well as they handle the presence of H/C.

NMR chemical coupling constants

An attempt was made to caluclate the coupling constants of the molecules using GAUSSVIEW. The calculations were run using the MPW1PW91 DFT method and the 6-31G(d,p) basis set with chlorform as the solvent. As the calculations sent to the scan are stopped after a certain period of time (approx~9hrs) this calculation failed. According to the log file it was purely a matter of not enough computational time that prevented any results being calculated. If this calculation had completed it would be expected that the coupling constants , specifically for the angle between the two hydrogens α and β to the lactam carbonyl would be more accurate then those determined using Janocchio. Janocchio uses empirical data and will therefore be less accurate than the semi-empirical DFT methods that were being employed here.

Infrared Spectra

To predict the vibrational frequencies of the bonds within the diastereoisomers GAUSSIAN was used and a calculation run on both molecules using the B3LYP DFT method and the 6-31G(d,p) basis set. Once these caluclations had been conmpleted the vibrational frequencies of several of the bonds within the molecules could be predicted and the infrared spectra also predicted.

Frequency/cm^-1	Corresponding bond
3827.08	O-H stretch
3626.86	N-H stretch
3184.64	H attached to C=C stretch
3157.06	methyl C-H asymmetric stretch
1790.90	C=O stretch

Frequency/cm^-1	Corresponding bond
3827.17	O-H stretch
3624.67	N-H stretch
3169.14	H attached to C=C stretch
3157.06	methyl C-H asymmetric stretch
1796.98	C=O stretch

Although there are no IR values from the literature to compare the calculated values to, the selected frequencies in the tables above are all in accordance with literature values. From the frequency calculations, the sum of electronic and thermal free energies are calculated and can be used to compare the difference in free energies between the two molecules. There was found to be a ΔG=1.91kJ/mol, with the minor product being the more thermodynamically stable of the two. Molecular mechanics theory using the MM2 force field predicted that the ΔG=1.37kJ/mol. As DFT calculations are proven to be more accurate than Molecular mechanics theory the actual value is liekly to be closer in value to 1.91kJ/mol.

Density Functional Molecular Orbital Calculations

GAUSSIAN was used to perform DFT based molecular orbital calculations. The density functional used was B3LYP and the basis set used was 6-31G(d). It was decided not to include p orbitals within the molecular orbital calculation as a compromise had to be made between computational time and accuracy and it is unlikely that having p-orbitals modelled onto the hydrogen atoms would have a large effect on the molecular orbital calculations due to the lack of anionic charge on the molecule.

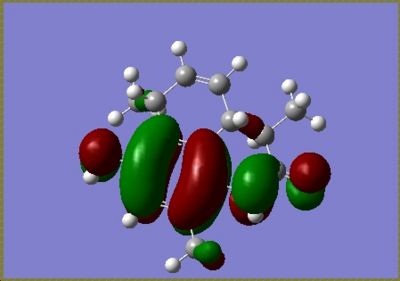
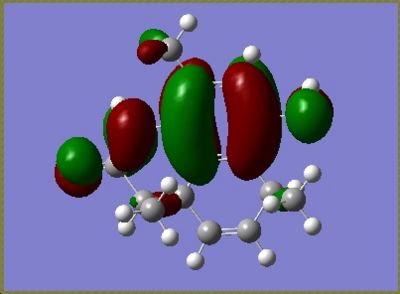
For the major isomer the HOMO and LUMO are as follows

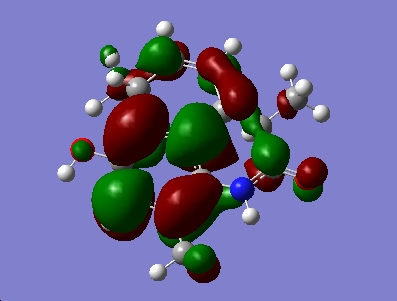The calculations also calculated the values of the orbitals which were converted into eV from Hartree, for the major isomer the HOMO = -5.39eV and the LUMO = -0.145eV and for the minor isomer the HOMO = -0.154eV and the LUMO = -5.38eV. These energy values are relative to an arbitrary point and do not represent absolute orbital energies.

For the minor isomer the HOMO and LUMO follow

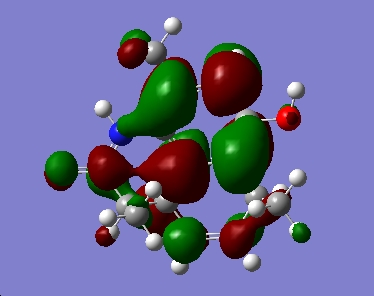In both isomers the HOMO lies across the C=C bond on the ring with only the methyl substituent. In the reaction scheme detailed in the journal the diastereoisomers were reported in, the molecule undergoes hydrogenation across this double bond. Addition reactions are well known to involve the HOMO, and the DFT MO calculation confirms that observation for these molecules.

Using the same method frequency calculation were repeated.

For the major isomer there were found to be some negative vibrational frequencies this means that there isn't an energy/geometry minimum.

Frequency/cm^-1 (6-31G(d,p) basis set)	Corresponding bond	Frequency/cm^-1 (B3LYP(d) basis set)
3827.08	O-H stretch	3862.75
3626.86	N-H stretch	3649.69
3184.64	H attached to C=C stretch	3202.08
3157.06	methyl C-H asymmetric stretch	3178.38
1790.90	C=O stretch	1821.12

Frequency/cm^-1 (6-31G(d,p) basis set)	Corresponding bond	Frequency/cm^-1 (B3LYP(d) basis set)
3827.17	O-H stretch	3885.56
3624.67	N-H stretch	3652.13
3169.14	H attached to C=C stretch	3179.98
3157.06	methyl C-H asymmetric stretch	3165.18
1796.98	C=O stretch	1825.89

Using the vibrational calculations the change in free energy was calculated and ΔG=1.65kJ/mol. The difference between this calculated value and the values calculated previously were most likely due to differences in the basis sets used for the calculations.

References

1. Density Functional theory, Ohio State University [2]
2. Gaussian Online Manual [3]