Org:sb807

Organic Computation Lab Module

Introduction

Throughout the course of this lab molecular mechanics calculations will be used to model contributions the overall energy of molecules. Molecular mechanics works by computing different terms that contribute to the steric energy. Some of the ones employed in this computational exercise (using ChemBio 3D ultra) are briefly:

[Stretch] - The bond stretching term

[Bend] - The bond angle term

[Torsion] - This term describes the torsion around a bond

[Non-1,4-VDW] -The Van Der Waal interactions between anything that doesn't have a 1,4 relationship

[1,4-VDW] - The Van Der Waal interactions between anything that does have a 1,4 relationship (and everything else that isn't already included!)

So now we know what MM2 tries to calculate on ChemBio 3D, how do all these separate terms manifest themselves? If we take a look at a simple molecule like ethane and perform an MM2 calculation: The overall steric energy is 0.8181 kcalmol^-1. To this the contributions are: 0.0251 from the [stretch] term, 0.0882 from the [Bend] term, and 0.694 from the [1,4-VDW] term. There is no torsional strain as only single bonds are present so the [Torsion] term is 0. This is a very simple example and although MM2 has its limitations (which will most likely be highlighted through this module) it is still very powerful tool that can carry out much more complex calculations than the one show here.

The Hydrogenation of a cyclopentadiene dimer

Exo/Endo Classification

The key difference in structure of the two cyclopentadiene dimers was that one was endo, and the other exo. Endo/Exo isomerisation is commonly found in the products of Diels-Alder reactions. The reason for this is because Diels-Alder reactions can easily produce bicyclic and tricyclic compounds, where one cyclic part of the molecule is actually bridges across the molecule. The definition of Exo and endo are

Exo: The Functional group or subsitutent is furthest from the 'longest bridge'.

Endo: The Functional group or subsitutent is closest to the 'longest bridge'.

The terms 'longest bridge' and 'shortest bridge' refer to the number of atoms in the bridge. In the case of dicyclopentadiene the compound has a double bond functional group in the 5 membered ring. The different isomers are identified below: (The longest bridge is shown in red)

(Left) Exo-Dicyclopentadiene (Right) Endo-Dicyclopentadiene.

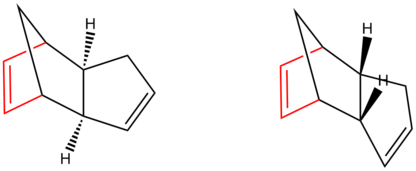
To determine whether the dimeration and hydrogenation are kinetically or thermodynamically controlled we can use a computational chemistry program. But first we have to establish what each compound (1-4) is

Compounds 1-4.

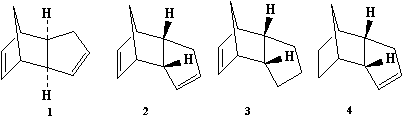
Using the definition of Exo/Endo Isomerism detailed earlier we can say that: Compound 1 is the Exo Dimer. Compound 2 is the Endo Dimer. Compound 3 is the Endo Dimer with the alkene in the 5 membered ring hydrogenated. Finally, Compound 4 is the Endo Dimer with the alkene in the 6 membered ring hydrogenated.

Optimising the geometry of the Endo and Exo Dicyclopentadiene

The energies of the Dimers can be computationally minimised using molecular mechanics. The energies of the exo and endo dimers are reported in table 1. The molecular mechanics calculation suggests that the energies of both compounds are very similar suggesting both products should form if the reaction is thermodynamically controlled. It has been shown experimentally however that the reaction only yields the 'endo' product.Another study (using MP3 analysis) also showed that transition state of the endo isomer is also lower in energy. This information implies that the reaction is kinetically controlled.

Table 1. All energies in Jmol^-1

Compound	Exo (1)	Endo (2)	Endo (3)	Endo (4)
Stretch:	1.2893	1.2923	1.2925	~ 1.0904
Bend:	20.5616	20.5681	19.8694	14.529
Torsion:	7.6704	7.6706	10.786	12.5046
H-Bond:	4.2368	4.2273	5.6268	4.5107
Total Energy:	31.8825	31.8856	35.6866	31.1659

Thermodynamic v.s. Kinetic for Hydrogenation

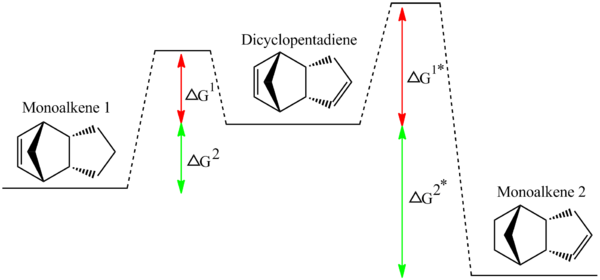
The two hydrogenated isomers have an overall energy difference of about 4.5 Jmol^-1. As compound 4 is significantly more thermodynamically stable than compound 3 if the experimental data leads to 4 forming over 3 then the hydrogenation reaction must be thermodynamically controlled. If however, the reverse is true i.e. the less thermodynamic product is formed experimentally, then this would suggest that the hydrogenation is kinetically controlled. Naturally there are only a few conceivable ways (in my education) of working out which alkene will hydrogenate. These are 1.To computationally perform some kind of analysis to see which one has a more stable TS. 2.To carry out the reaction in lab or find a literature source which provides the necessary information.

For the purpose of this exercise a literature source will suffice. Skala et al showed that the less stable monoalkene (1) forms over the more stable product (2) from a monohydrogenation reaction. Therefore we can conclude that the reaction is kinetically controlled. This implies that the transition state also has a lower energy for the kinetic product than the thermodynamic product. This is shown diagrammatically by the smaller energy barrier (ΔG1*) in the reaction profile for the kinetic product (i.e the one at a higher final energy).

Reaction profile for the monohydrogenation of Dicyclopentadiene

Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)

N-Methylpyridiniumoxazepenone

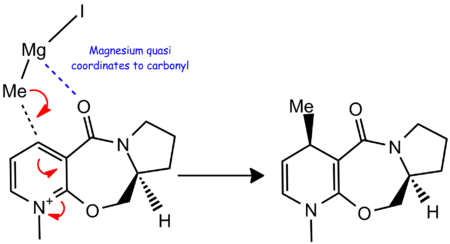
For the first reaction (compound 5 -> 6), the Grignard reagent selectively attacks the top face of the molecule (i.e the face anti periplanar to the hydrogen shown going into the plane). This kind of selectivity in a Grignard based reaction is unusual as Grigards are usually free to attack any face of a flat system (the aromatic in this case). If we use MM2 calculations on ChemBio 3D we can play around with the energies of the structure. Usually a structure has one energy minima which it continually reverts to, however this is not the case for the reactant, compound 5, as shown below in Table 2.

Table 2. Different confomations of compound 5 (all energies in Kcalmol^-1.

Conformation Isomer	Confomer 1	Confomer 2	Confomer3
Stretch	2.0347	2.0593	1.3302
Bend	14.2338	14.278	8.7068
Stretch-Bend	0.131	0.1327	0.137
Torsion	5.1343	5.04	13.4836
H-Bond	16.5247	16.5545	16.0402
Charge/Dipole	9.6258	9.5584	10.6399
Dipole/Dipole	-3.996	-4.0199	-3.921
Total Energy	43.1184	43.1206	44.7628
Carbonyl-Aromatic angle (Degrees)	11	9	-23
Face carbonyl sits on	Top	Top	Bottom
Jmol		(virtually the same as confomer 1)

From the table, we can see that the ChemBio 3D MM2 calculations do not necessarily compute the same energies for each conformation. This means there must be (at least) two energy minima for this molecule. The angle between the carbonyl and the aromatic ring (also included in the table) hints at the each minima corresponding to the amide carbonyl being on a different side of the aromatic ring (one above it, one below). Formations 1 and 2 have similar energies and each time the carbonyl is on the same face with a similar angle. If we manipulate the structure on ChemBio 3D of compound 5 we can run an MM2 calculation which produces a conformation where the amide carbonyl is on the bottom face of the molecule (by about 23 degrees). This has an energy slightly higher than when the carbonyl was sitting on the top face, yet is still a minima (just not the lowest minima). (The two main different formations can be seen in the table above as Jmol).

We can conclude quite comprehensively from these MM2 calculations that the thermodynamically stable structure is one where the carbonyl sits on the top face relative to the aromatic system by about 11 degrees, but now we must look at why the reaction is a stereoselective attack on the top face. The literature shows that when the grignard attacks the pyridium it is able to coordinate to the amide carbonyl via the electropositive magnesium ion. A reaction scheme is shown below. This ability to coordinate to the carbonyl means that the grignard delivers its methyl to whichever face the carbonyl is sitting on. Our MM2 calculations therefore tie in nicely with why the methyl stereoselectively attacks the top face.

Reaction mechanism for Grignard attack on Compound 5

Quinolinium Salt

Reaction mechanism for the aniline attack on the Quinolinium salt

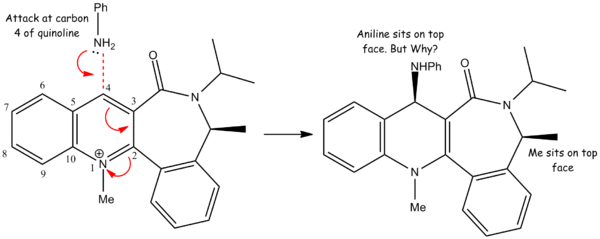
For this reaction an aniline molecule attacks a quinolinium salt stereoselectively on the top face. The aniline attacks carbon 4 of the quinoline fragment of the salt and the mechanism is shown above. It is unclear however why the mechanism is stereoselective towards the top face purely on examining the planar drawing above. Using ChemBio 3D we can model the energies of different confomers of the quinolinium salt to see how steric/electronic effects may influence the stereochemistry of the reaction.

Table showing the energies of different confomers of compound 7

Jmol	Dihedral angle	Energy (kcal/mol)
	8	86.3421
	-22	63.6270

The ChemBio 3D analysis has shown that their is a significant energy difference between a conformation where the oxygen sits below the ring and one where it sits above it. If we look carefully at the Jmol for the conformation with the lower energy the iPr group seems to be quite far from the C4 of the quinoline fragment. Comparatively when the carbon is above the plane of the molecule the iPr is twisted into a conformation where it hinders the C4 position slight more. As aniline is a bulky nucleophile it is like to be hindered by the iPr group sitting close (or closer relative to conformer 1) to the C4 carbon.

What other factors may contribute?

It has been shown by Leleu et al that the chiral axis strongly controls the diasteorelective reduction of NADH⁺ analogues. As shown by the diagram below if the aniline was a small compound such as a BH₃ and could coordinate to the carbonyl (like a lewis acid) it could selectively nucleophillically attack the bottom face. However in this reaction the nucleophile doesn't have an electropositive metal ion or lewis acid functionality and so on the contrary to reaction 5->6 it is repelled by the lone pairs on the oxygen and stericly hindered from attacking the bottom face.

Schematic adapted from the literature showing small nucleophile coordinating to carbonyl

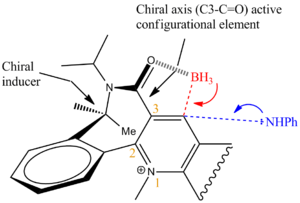
Conclusion

NADH⁺ is a pivotal compound used in reduction and oxidation of many bological reactions and biosyntheses (c.f. glycolysis). Using computational MM2 calculations we have successfully modelled and explained its reactivity and the reactivity of one of it's analogues. This potentially leads to better understanding of the enzyme and sucessively many biological systems. In general using MM2 calculations is also limited and we could improve our calculations by using gaussian to minimize the energy using techniques such as DFT-B3LPY i.e modelling the molecular orbitals not just the steric energy and its contributing factors! This is done by sending calculations to the SCAN system as we will see later on in this exercise.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

The key intermediate isomers 9 and 10 in the total synthesis of Taxol were synthesised using an oxy-cope rearrangement. The difference between the two isomers formed were that the cyclohexane ring fused onto it were either in the chair formation, or the twist boat formation. It is very possible that one of these isomers has a lower steric energy and therefore MM2 calculations should be more than sufficient to find out.

Taxol intermediates: Twist Boat(left), Chair(right)

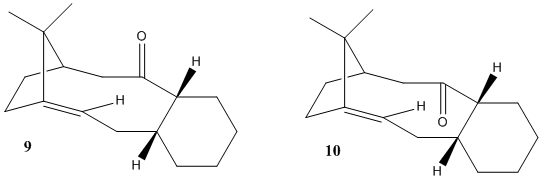
Determining the most stable isomer

Below are Jmols of the Taxol Intermediates. In the literature it is reported that the conformation known as compound 9 in this report has a twist boat form for the cyclohexane ring fused onto the 10 membered cyclic. Using MM2 calculations on both these structures we can identify that the chair form in both isomers produces a lower energy. The MM2 calculations show that compound 10 is the more stable isomer even though both can have chair forms of the cyclohexane ring.

Taxol intermediates

Intermediate	Jmol	Energy (kcal/mol)
9		48.8146
10		44.2652

But why does the alkene react slowly?

The product is thermodynamically unfavourable - After performing MM2 calculations on a hydrogenated equivalent of the alkene we discover that the product has a higher energy (xxx kcal/mol) with an increase in the bending and torsional terms. When an alkene becomes functionalised its geometry goes from being planar to non-planar (sp² to sp³ hybridization). In this instance, since the alkene is bound into the 9 membered being planar is actually favourable as changing to sp³ geometry brings with it a certain amount of torsional strain. This kind of result was documented by Schleyer et al in 1981 where a bridgehead caused an alkene (as it does here) to become strained when hydrogenated.

Modelling using semi-empirical Molecular Orbital Theory

Introduction

Part 1: Orbital control of reactivity

The literature MO calculations were done using PM3 calculations, whereas for this excercise PM6 calculations were employed by the ChemBio 3D software. Before the PM6 calculations could be done the energy of compound 12 had to be minimised. MM2 although insufficient for the follow calculation is still the prefered choice. The minimised energy is tabulated below.

Table 6. Energy contributions for Compound 12

	Post MM2 minimise kcalmol-1
Stretch	0.6141
Bend	4.7919
Stretch-Bend	0.0413
Torsion	7.6236
1,4 VDW	5.7893
Dipole/Dipole	0.1119
Total Energy	17.8982

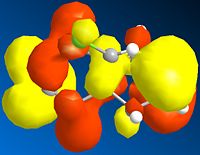
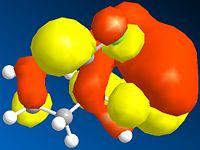
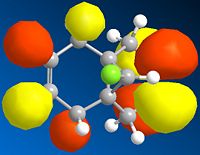
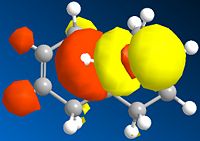
Below is a gallery of the images of the MOs in question (NOTE: Yellow is negative wavefunction, and orange positive ):

HOMO-1

HOMO

LUMO

LUMO+1

LUMO+2

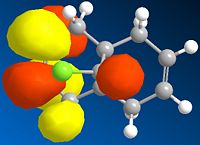The PM6 calculation results show the concentration of the wavefunction around the molecule. In organic chemistry, when a nucleophile and electrophile come together the interaction (in wavefunction terms) is between the LUMO of the electrophile and HOMO of the nucleophile. The MO calculations clearly discriminate between the two alkenes in this compound. This conclusion is drawn from the fact the LUMO is located more densely around the anti alkene to the chlorine. The HOMO in antagonistic fashion is located heavily on the syn alkene to the chlorine. Therefore we can conclude from the calculations performed that the anti alkene is electrophillic and the syn alkene nucleophillic.

Below are the MOs calculated using PM3 calculations taken from the literature, as mentioned. Here only the HOMO is shown, and it is (in concordance to my calcutions) located heavily on the syn alkene.

HOMO-1

HOMO

LUMO+2

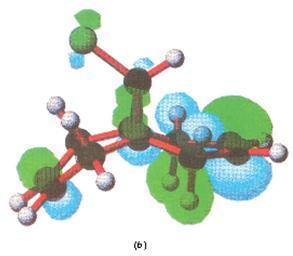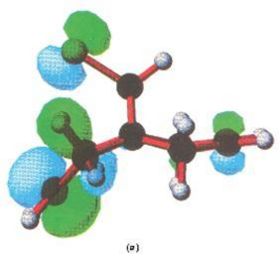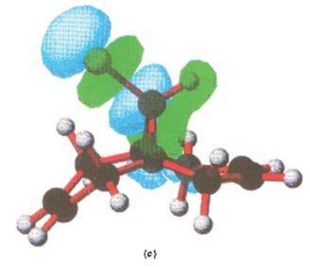Part 2: Influence of the C-Cl bond

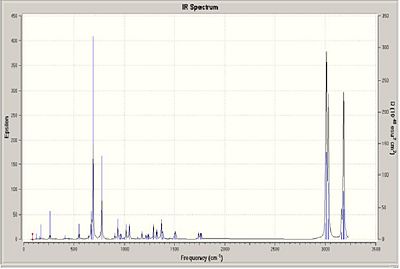
To measure how the C-Cl bond influences the vibrations of this molecule a density functional approach will be taken to compound 12 and compound 12.1 (a dihydro equivalent of compound 12, where the hydrogenated alkene is the one anti/exo to the C-Cl bond). The IR of the compounds are shown below.

Infrared Spectrum of compound 12

Infrared Spectrum of compound 12.1

If we look closely at compound 12 there seemes to be an overlap between the π_C=C bonding orbital of the exo alkene into the σ*_(C-Cl). If we examine the vibrational frequences of both molecules the table shows that the bond strength has increased on hydrogenation (i.e increasing wavenumber is proportional to increasing wavelength.) This means that there is indeed donation from the exo alkene π_C=C into the σ*_(C-Cl).

The effect of the C-Cl bond in compounds 12 and 12.1

Bond	Frequency (12) (cm-1)	Frequency (12.1)(cm-1)
C-Cl	772	912
Alkene Exo	1740	Hydrogenated
Alkene Endo	1760	1757

Structure based Mini project using DFT-based Molecular orbital method

Superacid activation of Quinoline

Introduction

Quinoline is an extremely important building block in the total synthesis of many different medicinal compounds. Due to the extensive research into its synthesis it has become a compound that is widely available and so computational study of its reactivity is extremely useful in the hunt for synthetic techniques and compounds in the drugs of tomorrow. In this lab we will study the superacid activation of quinoline followed by its reactivity with benzene.

Reaction scheme

It was repored in 2007 by Koltunov et al {ref} that upon activation by a strong acid, quinoline would form multiple N,C-diprotonated dications which would in turn react with weak nucleophiles. Therefore quinoline was able to undergo selective ionic hydrogenation with cyclohexane (in CF₃SO₃-SbF₅, HBr-AlBr₃-CH₂Br₂ acid systems) to give a 5,6,7,8-tetrahydroquinoline derivative. The quinoline also readily condenses with benzene (in HBr-AlBr₃) to produce 5,6,7,8-tetrahydro-5,7-diphenylquinoline. This diphenylquinoline derivative naturally has two different stereoisomers which will be extensively discussed later in the the report.

Quinoline is activated in superacid conditions and can form a diphenyl derivative in the presence of benzene

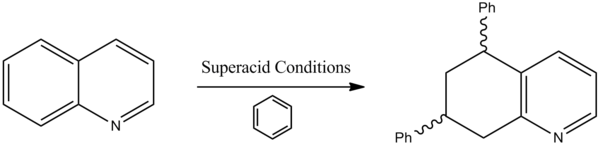
Mechanistic explanation

The first step of the reaction involves the tetra-hydrogenation of quinoline. As with any aromatic system hydrogenation is usually an unfavoured reaction, as it brings with it destabilization penalty. The energy of a quinoline compound post MM2 is 3.9542 kcalmol^-1. Its tetrahydro derivative however has a far greater energy of 9.2639 kcalmol^-1. Therefore this reaction must require extremely strong acidic conditions to get it kickstarted. A mechanism for the formation of the diphenyl derivative is shown below.

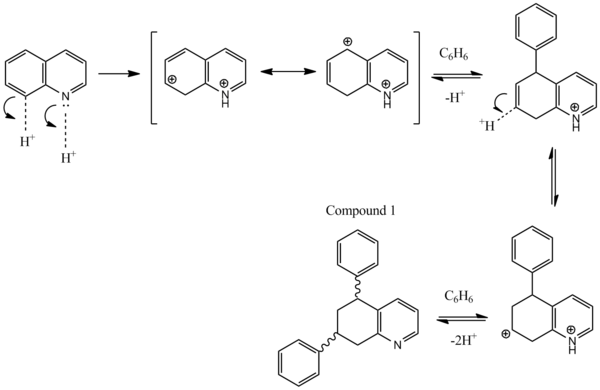
The alkylation occurs at carbons 5 and 7 on the quinoline system due to the stability via resonance of the wheland type intermediates. If the starting heterocycle had been isoquinoline instead of quinoline, then the phenyls would have alkylated at the 6, and 8 carbons as these produce wheland intermediates with more resonance forms.

Product rationale

Koltunov et al only reported two different isomers: cis and trans. However due to the nitrogen breaking the symmetry of the initial bicyclic, in theory 4 different isomers should form as there are two chiral centres. This type of isomerism is known as diasterisomerism. It was reported that the cis and trans form in a ratio of 3:1 respectively. The energies of the four products were calculated using ChemBio 3D and minimised using molecular mechanics.

Possible isomers from the superacid activation of quinoline in the presence of benzene.

Compound	Structure	Jmol	MM2 Energy (kcal/mol
W			13.3454
X		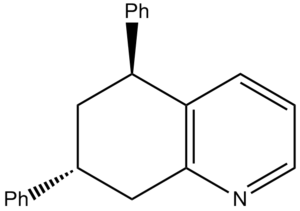	13.0278
Y		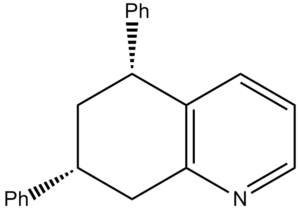	13.3012
Z		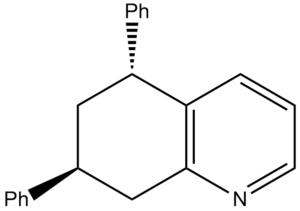	12.9154

Compound W and Y are actually stereochemically the same as they will just interconvert at room temperature. The formation where both are equatorial is mroe favourable than both phenyl groups being axial due to bulky steric groups.

NMR Analysis

The NMR was predicted by the GIAO approach using quantum mechanical density functional theory. The results are analysed below, but before this maybe it would help to try and predict just from inspecting the molecule what the NMR should look like.

5,6,7,8-Tetrahydro-5,7-Diphenylquinoline with all carbons numbered

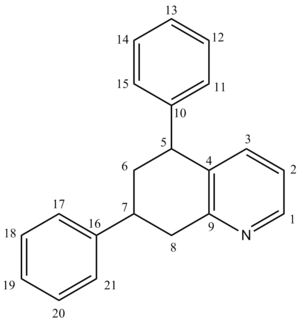
For Carbon-13 NMR a spectrum is usually run decoupled to avoid large J coupling constants (e.g 100-250Hz). Since the carbon nuclei are much bigger their relaxation times vary a far deal more for than for protons. This property manifests itself by certain carbons relaxing much faster than others and therefore producing larger than peaks on an NMR. Basically, single carbons will produce different sized peaks proportional only to ther relaxation time (not the number in that particular environment c.f H NMR).

For this compound there distinguishable carbons which can be spotted easily will be carbons 1 and 9 (as labelled above) as they're bonded directly to a Nitrogen atom and in a benzene ring. They will appear around 140 and 149 ppm respectively.

Carbons 2, 3, and, 4 should be at 122, 136, 129ppm respectively.

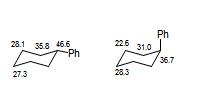
sp3 carbons with two hydrogens and two R groups such as 6 and 8 will appear around 20-30 ppm.

sp3 carbons with three R groups (where one is a phenyl) and one proton such as 5 and 7 will appear around 46 (Ph equatorial) and 36 (Ph axial).

Benzylic carbons like 11-15 and 17-21 will appear around 125-140 ppm.

Finally 10 and 16 can appear anywhere in a range of 20-40 ppm.

¹³C NMR

Literature vs Predicted NMR Comparison ¹³C NMR (CDCl₃) -

As shown below, the literature NMR can be quite difficult to interpret as it is a mixture of both Cis and Trans. Koltunov et al .managed to determine what oeaks belonged to which isomers by separating fractions of the product using flash chromatography and running successive NMR scans.

literature NMR, A mixture of cis/trans

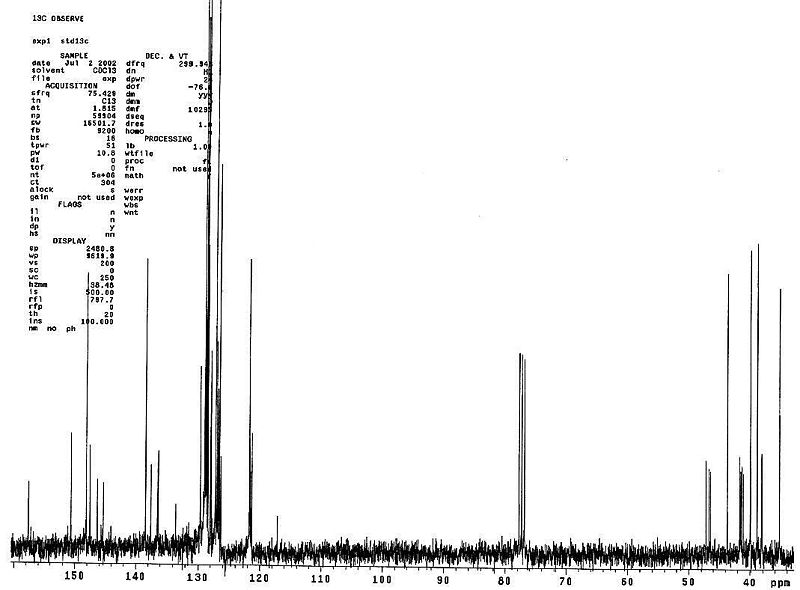
Below are the literature NMR tabulated (NOTE: There are 21 Carbons in the molecule however not all peaks are documented as some have the same ppm shift, and so they have been omitted).

13C NMR of literature cis/trans mix

spectra	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Literature(Cis))	40.6 (C7)	40.9 (C6)	41.1 (C8)	46.8 (C5)	121.2 (C3)	126.4	126.5	126.6	128.5	128.5	128.6 (5&7-Ph, C2-6)	134.8 (C10)	137.1 (C4)	145.1 (7-Ph,C1)	145.3 (5-Ph,C1)	147.2 (C2)	156.9 (C9)
Literature (Trans)	34.9	38.5	39.6	43.4	121.4	126.3	126.3	126.9	128.3	128.5	128.7	136	138.1	145	146.1	147.8	157.3

Fortunately Koltunov et al have already identified which shifts belong to which nuclei (NOTE: His labels are not the same as the ones I have used for the image above). For the basis of this experiment, we wish to determine which spectrum belongs to which isomer. As 13C NMR is such a sensitive and powerful tool we can determine from literature values whether a phenyl group is axial or equatorial (you may note that in my predicted NMR of the molecule I wrote that axial and equatorial phenyls influence the carbons they are attached to NMR shift).

Discussion and Summary:

1.If a phenyl group is equatorial the carbon to which it is attached (e.g. C5-Koltunov labelling) will have a ~46ppm shift

2.If the same phenyl is axial the carbon will have a shift at ~36ppm

Difference in axial and equatorial phenyls attached to a carbon

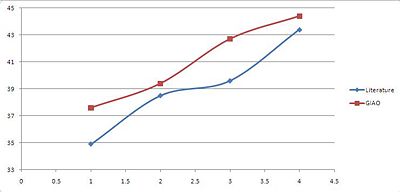
The GIAO NMR relevant shifts are tabulated below:

13C NMR GIAO predictions

Spectra	1	2	3	4
GIAO(Trans)	37.6	39.4	42.7	44.4
GIAO(Cis)	36.4	37.7	39.6	44.7

Trans: Literature vs GIAO NMR comparison for low ppm shifts (ppm is the x axis)

Trans: Literature vs GIAO NMR comparison for low ppm shifts (ppm is the x axis)

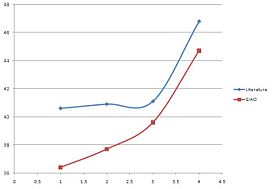We need to however be more specific with our comparison and due to the nature of the NMR prediction we can directly attribute whichever shift to that particular carbon. From the literature (cis) we know that the 2xPh-C have the assignments 40.6 and 46.8 ppm. We can then compare this specifically with the shift of thos particular carbons from the prediction which are: 36.4 and 46.7 respectively.

For the trans compound C5 is 43.4 ppm and C7 34.9 ppm. In the prediction they are 44.4 and 39.4 ppm respectively.

For both compounds one peak: C5 for the cis and C7 for the trans are very accurate i.e. within 0.1-1ppm of the literature. Due to the simple nature of the compound being analysed this is enough for use to distinguish between the two isomers however more evidence and a more sensitive tool would be required to be more confident with the results produced.

Conclusion

What are the reaons for the prediction not being so accurate?

1. The DFT minimization of the energy may not respresent the actual molecules. Therefore the NMR would produce predictions for nuclei which are not precisely in the correct magnetic field.

2. In experimental NMR studies there are certain innacuracies which are inherent in the design of the process which may not be included in the predicted NMR: Impurities, temperature effects, sample degradation to name a few.

---

References and citations

---