Optimization of metallic surfaces parameters
Before starting a calculation, it is good practice to perform a series of convergence test to find the most appropriate set of parameters for the system under investigation; the objective is to find best input setting to obtain a high enough accuracy while, at the same time, using the computational resources efficiently. This section contains a step-by-step tutorial on how to optimize these parameters for a metallic surface; platinum (Pt) is used as an example. To systematically find the best set of parameters, it is necessary to perform a series of single point energy calculations. To achieve this, it is much easier to use a set of scripts which can automate the process. First, it is useful to write a template input file (template.inp) which has the same structure of a traditional CP2K input; in this file, however, the relevant parameters are replaced by “markers” (in this example: LT_basis_set, LT_cutoff, LT_rel_cutoff, Kx, Ky, Kz). The automated scripts will search for these markers and replace them with a keyword and/or value from a list previously established. The scripts will then copy the file to a new CP2K input file and move it to a specifically created directory. It is important to remember that each parameter need to be optimized singularly; together, they then give the most suitable set of parameters for the system in exam. All the scripts and files described in this page can be found in the group's gitlab repository [1]. Additionally, this page contains workflows for extrapolating relevant parameters for a metallic system, such as the optimized lattice parameter, electronic structure and work function. Platinum is used as example for these sections as well.
Evaluating the numerical accuracy
The objective of performing convergence tests, as mentioned, is to find the best combination of accuracy and efficiency; using parameters which are unnecessarily strict can result in more expensive calculations without any significant improvement in the accuracy. To obtain a set of consistent parameters, the error associated to each of them needs be of the same order of magnitude as the others; generally, the error associated to the choice of the basis set is the one giving the biggest balance on the whole accuracy and could be taken as benchmark value. To understand the concept of error associated to a parameter, let us consider the following: a convergence test consists in a series of calculation where a parameter is varied over a range of values. The energy of such a set of calculations is considered to have converged when, upon variation of the parameter, the energy difference between calculations is negligible. The error is defined as the difference between the energy obtained with a specific value of the parameter and the converged energy. The fully converged energy is generally considered to be the one obtained from a calculation performed using the higher level of theory (e.g. more expanded basis set) or a more accurate parameter (e.g. larger cutoff, finer kpoint grid, etc.). The target accuracy strongly depends on the aim of the calculation.
Convergence Tests
Note: To use the scripts available on the GitLab repository, remember to modify #path_to_basis_set ad #path_to_pseudopotential in template.inp; these are the paths to the data files with the basis sets and the pseudopotentials. More details about the structure of a CP2K input file can be found in this page.
Basis set
- Running the set of calculations: to create the input files and run the calculations type
./Basis_set_run.sh. Given a list of basis sets (e.g. SZV-GTH-LDA-q18, DZV-GTH-LDA-q18, TZV-GTH-LDA-q18...), the script generates, for each of them, a directory containing a CP2K input and the pbs script. The input files are created by substituting the marker LT_basis_set in template.inp with the one of the basis sets in the list. The other parameters indicated by a marker are also set to a value provided in the script. The script then submits the calculations with each basis set from their respective directories. - Analysing the results: to analyse the results of this set of calculations, type
./Basis_set_analyse.sh. This script extracts the total energy from the CP2K output file in each directory and automatically converts it from Hartree to electronvolts. The values of energy obtained for each basis set are then printed into a new file, basis_set_TotEn.dat, which can be plotted to observe the variation of energy as a function of the basis set.
CUTOFF and REL_CUTOFF
- Running the set of calculations: to create the input files and run the calculations type
./Cutoff_run.sh. Given a range of cutoff values (e.g 50, 100, 150...), the script generates, for each of them, a directory (e.g. cutoff_50, cutoff_100,...) containing a CP2K input and the pbs script. The input files are created by substituting the marker LT_cutoff in template.inp, setting it to one of the values in the given range. The other parameters indicated by a marker are also set to a value provided in the script. The script then runs a calculation for each given value of cutoff. - Analysing the results: to analyse the results of this set of calculations, type
./Cutoff_analyse.sh. This script extracts the total energy the CP2K output file in each directory and automatically converts it from Hartree to electronvolts. The values of energy obtained for each cutoff are then printed into a new file, cutoff_TotEn.dat, which can be plotted to observe the variation of energy as a function of the CUTOFF.
To perform the convergence test for REL_CUTOFF follow the same steps using ./Rel_cutoff_run.sh and ./Rel_cutoff_analyse.sh instead.
For a more detailed description of the CUTOFF and REL_CUTOFF keywords in CP2K, visit this page.
k-point grid
There are several schemes to define the k-point grid; nowadays, one of the most widely used is the Monkhorst-Pack grid [1], which is an unbiased method of defining the k-points set for sampling the Brillouin zone:
where Gi are the primitive vectors of the reciprocal lattice and ni = 1, 2, .., Ni is a set of uniform points in each direction i. To perform a k-points calculation using a Monkhorst-Pack grid in CP2K, it is necessary that the following section is present in the input file:
&KPOINTS SCHEME MONKHORST-PACK Nx Ny Nz &END KPOINTS
where Nx, Ny and Nz (i.e. the number of points in the three dimensions) define an evenly spaced rectangular grid of dimension Nx Ny Nz. More details on the Monkhorst-Pack (and other k-points schemes) available can be found in the dedicated page of the CP2K manual. To perform the convergence test:
- Running the set of calculations: to create the input files and run the calculations type
./Kpoints_run.sh. Given a range of k-point values (e.g 2, 4, 6...), the script generates, for each of them, a directory (e.g. kpoints_2, kpoints_4,...) containing a CP2K input and the pbs script. The input files are created by substituting the markers Kx, Ky and Kz in template.inp, setting them to one of the values in the given range. The other parameters indicated by a marker are also set to a value provided in the script. The script then runs a calculation for each k-points grid. - Analysing the results: to analyse the results of this set of calculations, type
./Kpoints_analyse.sh. This script extracts the value of total energy from the CP2K output file in each directory and automatically converts it from Hartree to electronvolts. The values of energy obtained for each kpoint grid are then printed into a new file, kpoints_TotEn.dat, which can be plotted to observe the variation of energy as a function of the k-points grid size.
Extrapolation of relevant quantities
Equilibrium lattice parameter
In this section it will be shown how to calculate the equilibrium lattice parameter of a metallic system using the Murnaghan equation of states (EOS) [3] . The Murnaghan EOS relates the energy of a system to its volume. To find the equilibrium lattice parameter, the volume of the unit cell is changed by a few percentage points and the energy of the system for each new value of lattice parameter obtained. The resulting data is then fit using the EOS. To calculate the equilibrium lattice parameter you'll need the following files: template_lattice_param.inp, lattice_param_run.sh, lattice_param_analyse.sh, murn.x and, of course, job.pbs.
- Setting up and running the set of calculations: to create the input files and run the calculations type
./lattice_param_run.sh. Given a range of values for the pecentage change in volume, the script generates a set of inputs with different lattice parameters. Each input is then moved into a newly created directory (e.g. change_*), together with a copy of job.pbs. From each directory the calculation with the new value of lattice parameter is run. - Analysing the results: to analyse the results of this set of calculations you need to proceed in two steps:
- type
./lattice_param_analyse.sh. This script collects all the values of lattice parameters and energy from each cp2k output file and automatically generates two new files: energies.dat and murn.inp. The file energies.dat contains the values of lattice parameter (Å), volume (Å3) and energy (eV) obtained for each percentage change. The file murn.inp contains the data necessary to fit the values of energy vs. volume using the script murn.out; - To find the equilibrium lattice parameter type
./murn.x < murn.inp > murn.out. This will produce the file murn.out which contains the value of equilibrium lattice parameter. You can obtain it by typinggrep -A3 "alat=" murn.out.
- type
Electronic structure
DOS
Band Structure
CP2K offers the possibility to calculate the band structure of solids; to this end the following section needs to be added to the DFT section of the CP2K input file:
&PRINT
&BAND_STRUCTURE
ADDED_MOS 20
FILE_NAME platinum.bs
&KPOINT_SET
UNITS B_VECTOR
SPECIAL_POINT GAMMA 0.0 0.0 0.0
SPECIAL_POINT X 1./2. 0.0 1./2.
SPECIAL_POINT W 1./2. 1./4. 3./4.
SPECIAL_POINT K 3./8. 3./8. 3./4.
SPECIAL_POINT GAMMA 0.0 0.0 0.0
SPECIAL_POINT L 1./2. 1./2. 1./2.
SPECIAL_POINT U 5./8. 1./4. 5./8.
SPECIAL_POINT W 1./2. 1./4. 3./4.
SPECIAL_POINT L 1./2. 1./2. 1./2.
SPECIAL_POINT K 3./8. 3./8. 3./4.
SPECIAL_POINT U 5./8. 1./4. 5./8.
SPECIAL_POINT X 1./2. 0.0 1./2.
NPOINTS 500
&END KPOINT_SET
&END BAND_STRUCTURE
&END PRINT
For a detailed description of the relevant keywords, visit the dedicated page of the CP2K manual. A useful example explaining a CP2K input to get the band structure can be found in this page. This input produces an additional output file named platinum.bs. To convert platinum.bs to a file which can be plotted you can use the script bandstructure.out, which can be found in the GitLab repository. Before running the script, you need to know the Fermi energy of the system, which can be obtained as explained above. Once obtained the Fermi energy, you can run the script as follow:
./bandstructure.out
While running, the script will ask for the names of the input and output files and for the Fermi energy; in the case of the platinum slab, for example, it will go as follows:
Enter input file name: > platinum.bs Enter output file name: > bandstructure.dat Enter Fermi Energy (Hartree): > 0.5619
The script rearranges the energy values in platinum.bs in a way that can be plotted and automatically subtract the Fermi energy.
Work Function
The work function of a surface, W, is the minimum energy necessary to remove an electron from a solid to a point in the vacuum immediately outside the solid surface. Mathematically it can be defined as follows:
where -e is the charge of an electron, ϕ is the electrostatic potential in the vacuum nearby the surface, and EF is the Fermi level (electrochemical potential of electrons) inside the material. The term -eϕ is the energy of an electron at rest in the vacuum nearby the surface.
To calculate the work function using CP2K, first you need to add, in the SCF section of your input file, the following section:
&PRINT &V_HARTREE_CUBE ... &END V_HARTREE_CUBE &END PRINT
This will print an additional output file: a cube file containing the values of electrostatic potential generated by the total density. Now run the script aver.out, which you may find in the GitLab repository. To do this you you will need to:
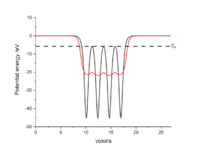
- Create the files input and cube from the cube file generated by CP2K. Check input-commented to understand how to write them. Remember to have both this files in the same directory as aver.out;
- Run the script by typing:
./aver.out < input. aver.out converts the data stored in cube into six new files which can be plotted. These files are: aver_X.dat, aver_Y.dat, aver_Z.dat, which contain the values of electrostatic potential in the X, Y, and Z direction and avermacro_X.dat, avermacro_Y.dat, avermacro_Z.dat, which contain the macroscopic average of the potential in the X, Y, Z directions. If your surface is perpendicular to the Z axis, the data along Z will be the ones you are interested in for the calculation of the work function; - From the value of Fermi energy and the value of electrostatic potential energy in the vacuum region (flat region in the plot) you can now calculate the work function. The Fermi energy can be obtained from the CP2K output file (e.g cp2k.out) by typing:
grep 'Fermi energy:' cp2k.out.
References
<References>
- ↑ Monkhorst, H. J., Pack, J. D., Special points for Brillouin-zone integrations, Phys. Rev. B, 13, 5188-5192, 1976, 10.1103/PhysRevB.13.5188
- ↑ Simon, S. H. The Oxford Solid State Basics, Oxford University Press, 2013
- ↑ Murnaghan, F. D., The compressibility of media under extreme pressures, Poceedings of the National Academy of Sciences, 30, 244-247, 1944, 10.1073/pnas.30.9.244
