ONIOM for conical intersections

Describe a conical intersection

We now turn our attention to the location of surface crossings, or conical intersections, with ONIOM. A conical intersection is a structural bottleneck, through which ultrafast radiationless decay is possible between excited- and ground-state potential energy surfaces.
The intersection hyperline is (N - 2) dimensional, where N is the number of nuclear degrees of freedom. The plane that lifts the degeneracy is formed by the gradient difference (x) between the two states and the derivative coupling (y); these vectors comprise the branching space. The states are no longer degenerate when the geometry is distorted along these two linearly independent nuclear coordinates (x) and (y) :

x	$=\frac{\partial (E-E^{*})}{\partial q}$
y	$=⟨C^t(\frac{\partial H}{\partial q})C^{*}⟩$

When the energy is plotted in the branching space, the potential energy surfaces form a double-cone structure, i.e., a reaction funnel, through which multiple ground-state products can be formed, depending on the shape of the crossing and the reaction pathways that can be accessed from it.

Standard geometry optimization methods can locate critical points along the (N - 2) dimensional hyperline using a modified gradient :

$\tilde{g}=2(E^{*}-E)\frac{x}{|x|}+P\frac{\partial E^{*}}{\partial q}$

The first term on the rhs of this equation takes the system to the intersection space, while the second term minimizes the energy within the hyperline. P projects the gradient of the excited state onto the orthogonal complement of the x,y plane that lifts the degeneracy.
This is the intersection space, which to first order preserves the degeneracy of the electronic states.

For ONIOM conical intersection searches, we assume that the excitation is localized in the model system and that the interaction between the regions is the same for ground state and excited states. So, the energy difference between the states is then determined by the high-level calculation only.
This implies that only the high-level calculation on the model system determines the degeneracy.

ONIOM method combinations were evaluating by comparing energies and geometries of an $S_0$/$S_1$ conical intersection and nearby $S_1$ minimum for previtamin D.
For the $S_1$ minimum, CLS* is not an approximation beyond that intrinsic to ONIOM, since we use excited state methods for the low level as well as the high level, and the energy and gradient are integrated from three excited-state subcalculations. However, for the conical intersection, both CLS and CLS* are approximations, in the sense that the gradient difference and derivative coupling vectors which determine the projected $S_1$ gradients are only determined here from the high-level model calculation.

The modified gradient for conical intersection searches for ONIOM can therefore be written as

${\tilde{g}}^{ONIOM-CLS}=2(E_{model}^{*,high}-E_{model}^{high})\frac{x_{model}^{high}}{|x_{model}^{high}|}+P^{\prime }\frac{\partial E^{*,ONIOM-CLS}}{\partial q}$

where

$x_{model}^{high}=\frac{\partial (E_{model}^{high}-E_{model}^{*,high})}{\partial q}=\frac{\partial (E_{model}^{high}-E_{model}^{*,high})}{\partial q^m}J$

and P′ is determined using $x_{model}^{high}$ and $y_{model}^{high}$ (with the configuration coefficients for the high-level calculation):

$y_{model}^{high}=⟨C^t(\frac{\partial H_{model}^{high}}{\partial q})C^{*}⟩=⟨C^t(\frac{\partial H_{model}^{high}}{\partial q^m})C^{*}⟩J$

Since the modified gradient ${\tilde{g}}^{ONIOM-CLS}$ only dependson x and y from the high-level calculation on the model system, the additional computational cost of ONIOM will be no more than if we were studying the model system alone. (Note that P′ is sparse, and the nonzero space is determined only by the size of the model system.)

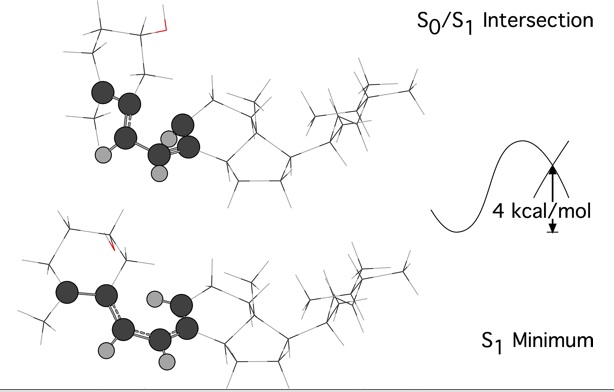Figure 3

Next part ONIOM for transition structures

Back to ONIOM tutorial (G03)