Nm1916mrd
H̠-H2
What value do the different components of the gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface?
The reaction pathway represents the path of lowest potential energy of the system. The 'reaction pathway' is quite confusing here. At first I thought you meant the trajectory (the black line). I think what you mean is the minimum energy path --Sw2711 (talk) 16:46, 23 May 2018 (BST)The minimum potential energy along this pathway corresponds to when atoms B-C have a bond formed between them and A is at infinity or when there is a bond between A-B and C is at infinity. Therefore, this description is not very clear either, even though I sort of could guess what you mean. But again, you can always have a minimum energy at any point (any length of AB or BC) along the reaction coordinate--Sw2711 (talk) 16:46, 23 May 2018 (BST)If there is a bond formed between 2 atoms there is slight variation in energy and position due to the bond vibrating, indicated by the oscillating path on the contour plots. If there is a bond between B-C and A is brought towards B, the potential energy along the reaction pathway will increase to a point until A-B = B-C. Is it important to have AB=BC for a TS?--Sw2711 (talk) 16:46, 23 May 2018 (BST) This point is the transition state, which is the maximum potential energy along the reaction pathway for both the A-B and B-C direction. This point also corresponds to a minimum in the orthogonal direction therefore is a saddle point. The last two sentences are quite good. But how do you identify whether it is a local minimum, local maximum or saddle point by using partial differential equations? Have a look at this video, if you are not sure. link--Sw2711 (talk) 16:46, 23 May 2018 (BST)
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.
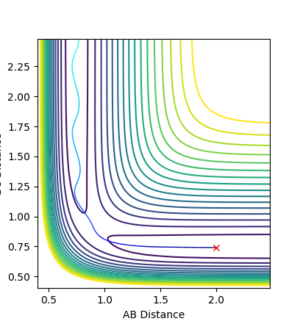
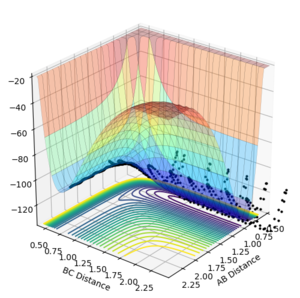
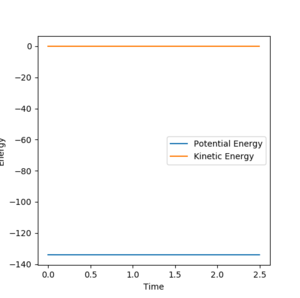
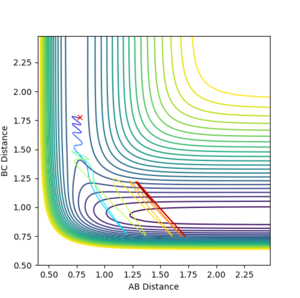
The transition state occurs when A-B = B-C which equals 0.908. This was found by letting the momentum equal 0 ad then through trial and error. At this point the distance between A-B and B-C does not oscillate, The system is at the bottom of the potential well in the direction when r1=r2 and at a maximum in the direction orthogonal. This results in the system being stationary with respect to time i.e. A-B and B-C do not move. Your explanation is good. Just one point, when you keep repeating the fact that A-B=B-C, I'd feel like you are emphasising it is a very important factor to find the TS. But that is not really true--Sw2711 (talk) 16:58, 23 May 2018 (BST)This can be seen from the picture below:
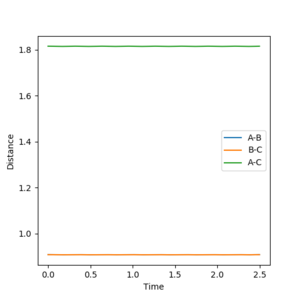
Comment on how the mep and the trajectory you just calculated differ.
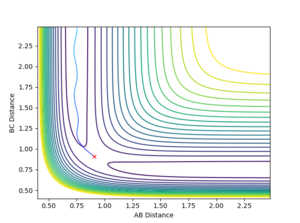
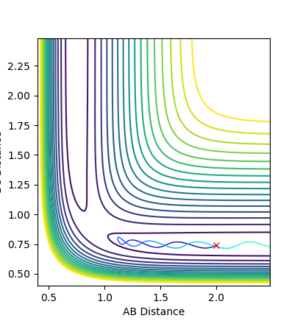
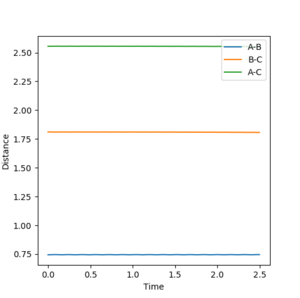
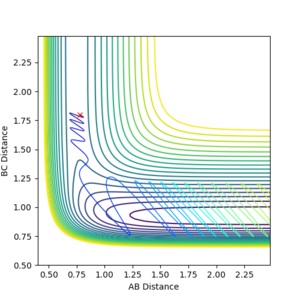
Under the MEP calculation, the system does not oscillate with time. This is due to the velocity resetting to 0 at every calculation which corresponds to 0 kinetic energy. Whereas under dynamic calculation, the loss in potential energy corresponds to a gain in kinetic energy, which shows as a vibrations. This is clear from the contour plot below with the MEP calculation and dynamic shown respectively.

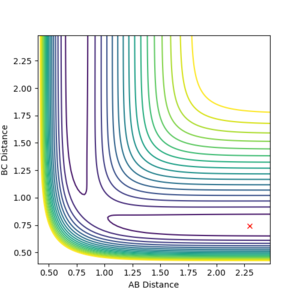
If we take the positions and momenta from the first example, You need to tell me the condition--Sw2711 (talk) 16:58, 23 May 2018 (BST) it is clear to see under the MEP calculation that the reaction does not occur, the system does not reach completion, whereas under dynamic calculation, the reaction reaches competition. The reason that the system under MEP does not complete is the fact that there is 0 kinetic energy therefore the molecules arent moving towards eachother. So does it move at all? If your answer is 'no, they don't move at all', then it is not true. The MEP trajectory move along the lower energy path. You can increase the number of steps to see a longer trajectory--Sw2711 (talk) 16:58, 23 May 2018 (BST)Since they dont collide a reaction canot happen.
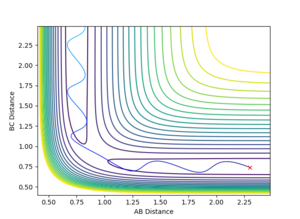
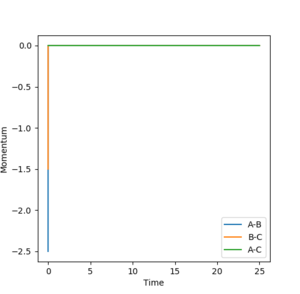
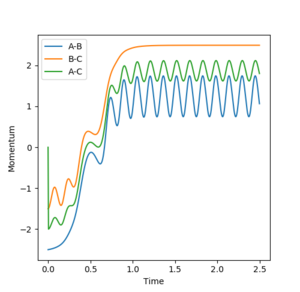
Reactivity at Different Momenta
| p1 | p2 | Energy | Reactive | Number | |
|---|---|---|---|---|---|
| -1.25 | -2.5 | -99.018 | Yes | 1 | |
| -1.5 | -2.0 | -100.456 | No | 2 | |
| -1.5 | -2.5 | -98.956 | Yes | 3 | |
| -2.5 | -5.0 | -84.956 | No | 4 | |
| -2.5 | -5.2 | -83.416 | Yes | 5 |
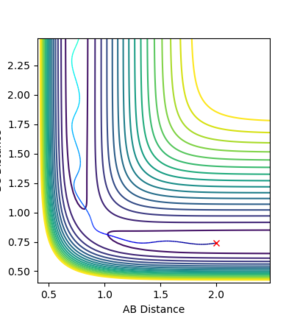
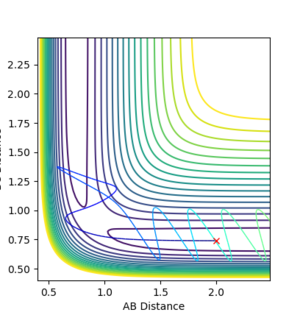

It is clear that whether a reaction occurs or not depends on the initial momenta of the system. ̆The system needs enough energy to pass over the TS energy barrier, however the product still may not be formed if there is enough energy present in the system to recross the transition state.
This part is good--Sw2711 (talk) 16:58, 23 May 2018 (BST)
Transition State Theory
Transition state theory is used to describe chemical reactions in terms of potential energy surfaces and position of the molecules involved in the reaction. It assumes that the transition state formed is long lived enough to have a Maxwell Boltzmann distribution of energies. It also assumes that the atomic nuclei obey classical mechanics and not quantum mechanics. In quantum mechanics there is always a finite possibility that when a nuclei collides encounters an energy barrier, it can tunnel through, whereas classically whenever a particle has energy below the energy of the surface,it will never pass. Since the nuclei will have quite a low mass, there is a realistic chance that it could tunnel on some occasions, with this assumption neglecting this.[1] The transition state theory also assumes that once the product is formed, there can be no recrossing of the energy barrier. It is clear from figure 11 and 12 above that the energy barrier has been recrossed, in figure 12 multiple times therefore there is deviation from this theory and experimental results. Good observation and comparison of the TST and your results. One minor point, I think the term ‘distribution' is not very applicable here. ‘distribution’ is mainly used in statistical thermodynamics. But in terms of your system, there are only 3 atoms. So, it is either one way or the other. --Sw2711 (talk) 17:00, 23 May 2018 (BST)
F H H System
Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved? It can be seen from the images below that the reaction of H-H with F is an exothermic reaction as the products are lower in energy than the reactants. This is because the F-H bond is strong due to the large electronegativity difference between the 2 atoms, giving the bond some ionic nature. On the otherhand, the reaction of H-F with H is endothermic i.e. the products are higher in energy than the reactants as the homo nuclear bond is much weaker.
Good--Sw2711 (talk) 17:17, 23 May 2018 (BST)

Locate the approximate position of the transition state. The location of the transition state can be found by running the MEP calculation and finding where the maximum is when the momentum of all molecules is 0. Interesting, I'd like to see a MEP figure showing the maximum.--Sw2711 (talk) 17:17, 23 May 2018 (BST)By switching back to dynamic calculation and varying the distance between H-H and F-H the transition state can be found when there is no change in any of the positions on the inter nuclear distance vs time graph which can be seen below. The transition state occurred when the H-H distance was 0.744 Å and the H-F distance 1.811 Å. Hammonds postulate helped locate the TS as it is clear the transition state would be closer to F + H-H as this is higher in energy, therefore the search was started closer to the products H-H. Otherwise, good. --Sw2711 (talk) 17:17, 23 May 2018 (BST)
Report the activation energy for both reactions. The activation energy can be found by altering the H-H and F-H distance such that the system will no longer be in the TS, it will fall into either the reaction or products. Under MEP calculation, by increasing the H-F distance towards infinity, the potential energy of the H-H reactants can be found(The H-F distance is increased until the potential energy value was a constant). The (TS energy - reactant energy) will then give the value of the activation energy. The same can be done for the H-F activation energy by increasing the H-H bond distance to infinity.
Good, but I'd like to see how to find the PE of TS too. --Sw2711 (talk) 17:17, 23 May 2018 (BST)
PE of TS = -103.752 kcal/mol
PE of H-H = -104.019 kcal/mol
PE of H-F = -134.008 kcal/mol
Activation Energy for H-H to H-F= 0.267 kcal/mol = 1.117 kJ/mol
Activation Energy for H-F to H-H= 30.256 kcal/mol = 126.591 kJ/mol

There is a much greater activation energy for H-F to H-H as H-F is a much stronger bond to break and the reaction is also endothermic.
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
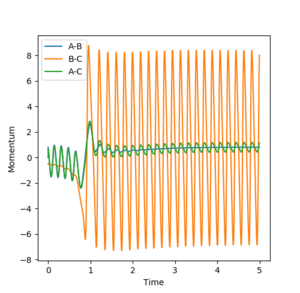
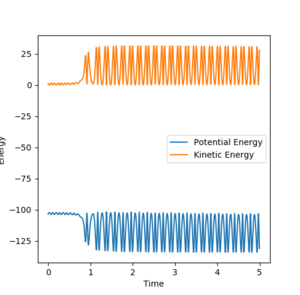
From looking at figure 18 it is clear that when a H-H molecule collides with a F atom it is a very exothermic reaction. This can be seen by the large increase in amplitude of the vibrations in the products. In exothermic reactions, the energy produced is usually either transferred to the molecule as vibrational energy or translational energy. This could be measured experimentally by using a calorimeter, as the increased vibrations and translational motion would increase the temperature, hence enthalpy can be measured and related to KE energy. It is clear from figure 20 that energy is conserved as when PE increases KE decreases and vice versa. Good, so how do you measure the enthalpy? --Sw2711 (talk) 17:17, 23 May 2018 (BST)
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state. From Hammonds postulate we know that if the TS is closer in energy to the reactants, there will be an early TS whereas if the TS state is closer in energy to the products , the TS state will be late. Polanyis empirical rules state that vibrational energy is more efficient in activating a late transition state than translational, whereas for an early TS, translational energy is more efficient than vibrational. [2] It is clear that for an exothermic reaction which has an early TS, the energy of the reactants is higher than the energy of the products, therefore excess energy is released in the form of vibrational energy(seen in section above), however translational energy decreases to conserve energy. On the otherhand, for an endothermic reaction with a late TS, the translational energy increases from reactants to products, with a decrease in vibrational energy. Therefore it is clear that translational energy in the reactants has more of an impact if the TS is early, whereas vibrational energy has more impact if there is a late TS state- this agrees with Polanyis empirical rules.
The example below shows this which is H-H forming H-F an exothermic reaction with an early TS. By keeping the total energy into the system the same but varying what form the energy is in, the reaction either completes or does not. When more of the energy is in the form of translational motion, the reaction occurs, whereas when more is in viibrational form it does not.
Good explanation of the theory. But I'd like to see your initial settings. How did you vary what form the energy is in? Are the total energy the same in both Figure 21 and 20? To me, it looks like Figure 20 may just not have enough energy overall? For Figure 21, it would be better if you could increase the number of steps to make sure that the product has formed. It is possible that a system in a situation as Figure 21 would still re-cross the TS. --Sw2711 (talk) 17:17, 23 May 2018 (BST)
The opposite is true for an endothermic reaction with a late TS- need energy in vibrational form in order to get reaction to occur.
