NEWPAGE
Introduction to Computational Chemistry
The quote by Schleyer that ‘’computational chemistry is to model all aspects of chemistry by calculation rather than experiment’’ tells us that practically every mechanistic question can be tackled by computational methods. This is true in principle but says nothing about the quality of the computed numbers, and Coulson said, ‘’Give us insights, not numbers’’, which emphasises this point and relates to the fact that it is easy – fortune or curse – to compute numbers. Applying computational techniques to chemical problems requires a careful choice of the theoretical methods. Basic knowledge of the capabilities and the drawbacks of the various methods is an absolute necessity.
Molecular Mechanics (MM) force fields (MMFF) make use of empirical formulae to approximate the interatomic interactions in an average fashion with a variable set of corrective terms to account for electronic interactions that are not included by design. MMFF computations are attractive for the quick determination of molecular structures and heats of formation that are typically in excellent agreement with results of higher level computations, however rely on mechanics only. The method produces bond lengths that are accurate to 0.01 Å, whereas conformational energies and vibrational frequencies to 1 kcalmol-1 and 20-30 cm-1, respectively.
In contrast to molecular mechanics force fields, modern semi-empirical methods are classified as an SCF electron-structure theory (wavefunction-based). In line with chemists’ valence electron models of chemical bonding, only valence electrons are taken into account in the computational method. To avoid the interaction of every electron with every other electron, multicentre integrals are neglected and empirical corrections based on experimental results are added. A key advantage of semi-empirical methods is that they give heats of formation directly. Small cyclic hydrocarbons are typically computed to be too stable and sterically crowded structures are predicted to be unstable. Semi-empirical methods do not describe weak interactions like London dispersion forces well, thus they would not be suitable to compute molecular structures that rely heavily on hydrogen bonding.
The main objective of Density Functional Theory (DFT) is to replace the many-body electronic wavefunction with the electron density as a simpler quantity to deal with. It requires considerably less computer time and disk space than ab initio computations, making it easier to deal with much larger atoms and molecules. The methods described above have been employed in the assignment. Comparison of literature results with the computational outcome (wherever possible) allows for a more profound analysis of molecular mechanisms, interesting visualisations and last but not least, understanding of the reactions and their underlying principles.
Hydrogenation of Cyclopentadiene Dimer
Exo/Endo Selectivity in Dimerisation of Cyclopentadiene
Dicyclopentadiene (cyclopentadiene dimer) is found in coal tar and is relatively easy to extract at a low cost. At 170°C, the boiling point of dicyclopentadiene, it reverts to its monomer which can be obtained by distillation. The dimerisation is a Diels-Alder self-condensation. The system is described as a π4s + π2s cycloaddition. There are 2 possibilities of this interaction: both bonds can form on the bottom face of the diene (π4s) and both bonds form on the top face of the alkene (π2s), giving the exo adduct or alternatively, bonds can form to the bottom face of the alkene (π2s), giving the endo isomer.[1]
The Diels-Alder reaction is one of the most interesting and at the same time extremely important reactions in synthetic chemistry because it forms two carbon-carbon bonds in one step and is one of the few methods available for forming cyclic molecules. A molecular orbital description is often used to account for the reactivity and stereochemistry of the reaction. The HOMO of the diene donates electrons into the LUMO of the dienophile, resuling in a cyclic non-polar TS and cyclic product. Secondary orbital overlap can account for the preferred (not always) formation of the endo adduct. Other factors such as the volume of activation or dipole considerations are important but will not be discussed.[2] MM2 method was used to optimise the geometry of each cyclopentadiene isomer in search for the minimum energy conformation adopted by the molecule. The results are presented in Table 1.
| Structure | Stretch | Bend | Stretch-Bend | Torsion | Van der Waals | Dipole-Dipole | Total Energy |
|---|---|---|---|---|---|---|---|
| Exo Isomer | 1.29 | 20.58 | -0.84 | 7.65 | 4.23 | 0.38 | 31.88 |
| Endo Isomer | 1.25 | 20.85 | -0.84 | 9.51 | 4.32 | 0.45 | 34.00 |
The exo isomer has a lower total energy in comparison with the endo isomer. The latter is hence more thermodynamically stable by 2.12 kcalmol-1. The main difference between the adducts lies in the torsion energy which is 1.86 kcalmol-1 greater for the endo isomer. Its destabilisation can be attributed to the two eclipsing relationships in the endo transition state of the atoms in a 1,4-location to each other. In the exo isomers bond torsion is absent due to distortion of the same set of atoms.
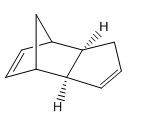
Structure 1 |
Structure 2 |
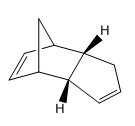
Nevertheless, the exo product is almost always the minor product. The reaction favours the less thermodynamically stable endo adduct, also called the kinetic product of the reaction formed under kinetic control. This involves lower temperatures and shorter reaction times, which ensures that only the fastest reaction has the chance to occur. The molecules following the lower activation energy pathway form much faster. In contrast, to ensure thermodynamic control, one must employ higher temperatures and long reaction times to ensure that even the slower reactions have a chance to occur and all the material is converted to the most stable compound. The endo adduct will still be favoured.[3] Illustration of this concept can be found in Figure 1. [4]
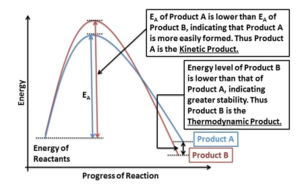
The exo product, even though shown to be thermodynamically more stable, has a higher transition state barrier to surmount and is therefore the minor isomer formed. Important evidence for this observation is provided by Baldwin who refers to the thermal isomerisation of the endo-dicyclopentadiene to exo-dicyclopentadiene at 180-240°C. At such temperatures there is enough thermal energy to establish equilibrium between the two adducts and the most stable one will be formed preferentially. It was also noted that to achieve dicyclopentadiene cracking, one has to transform the exo isomer intramolecularly to the endo equivalent which then undergoes cycloelimination to give two cyclopentadiene monomers.[5] This reaction profile (coming from the same journal) clearly showing both kinetic and thermodynamic control products, can be found in Figure 3.

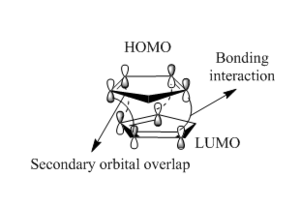
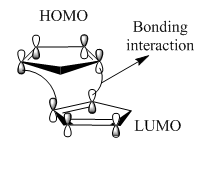
Why is the exo product more stable? This is because the bridges formed across the ends of the new bonds eclipse the attached five-membered ring resulting in a less strained structure. Why is the endo isomer formed faster? The endo preference under kinetic control can be explained using the concept of frontier orbitals. There is a favourable across space interaction between the LUMO of the dienophile and the HOMO of the diene that does not lead to bond formation and is hence referred to as the secondary orbital overlap. SOO makes the transition state leading to the endo adduct lower in energy and hence its formation is significantly faster than in the exo isomer where such an interaction is absent.[6] This is illustrated in Figure 4 and 5.
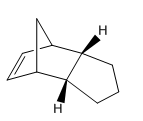
Hydrogenation of Endo Cyclopentadiene Dimer
The endo cyclopentadiene dimer participates in hydrogenation reactions to yield two possible dihydro derivatives. Employment of prolonged reaction times leads to the formation of a tetrahydro product. In order to evaluate the stability of the dihydro derivatives, the MM2 force field derived energy calculations must be discussed.
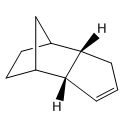

Structure 3 |
Structure 4 |
The MM2 contributions to the total energy can be found in Table 2. Structure 4 is more thermodynamically stable than compound 3 and the difference is 4 kcalmol-1. The main component to the energy values is bend. Distortion of bond angles from their ideal values causes destabilisation of the molecule because of the excess of potential energy being stored in molecule. For sp2 hybridised carbons the optimal angle is 120°, whereas in sp3 hybrids the angle is 109.5°. The C=C-R angle in structure 3 is found to be 107.8°, whereas in molecule 4 the value is 113.0°. The angle displacement from equilibrium values is most pronounced in molecule 3, which, as a result, experiences significant angular strain. This makes it less thermodynamically stable than molecule 4.
| Structure | Stretch | Bend | Stretch-Bend | Torsion | Van der Waals | Dipole-Dipole | Total Energy |
|---|---|---|---|---|---|---|---|
| Structure 3 | 1.2771 | 19.8664 | -0.8346 | 10.8068 | 5.633 | 0.1621 | 35.69 |
| Structure 4 | 1.0974 | 14.5249 | -0.5493 | 12.4978 | 4.5109 | 0.1406 | 31.15 |
It is difficult to discuss the type of control employed in the reaction. Structure 4 is more stable than 3, hence under thermodynamic control it will be the major product. To determine whether a product is kinetic, investigation of its TS activation barrier height is necessary because a compound that forms the fastest has the lowest energy barrier to surmount.
Stereochemistry and Reactivity of Intermediate in Synthesis of Taxol
Atropoisomers are conformers which, owing to steric hindrance or electronic constraints, interconvert slowly enough (by definition, with a half-life of > 1000 s) that they can be isolated..[7]
Paquette analysed the value of the oxy-Cope rearrangement to organic synthesis and in his work he presented the reaction shown in Figure 4. Carbiniols of this type are known to undergo atroposelective anionic oxy-Cope rearrangements to form structures with X = Y = H, which are key intermediates in the total synthesis of a mitotic inhibitor Paclitaxel, employed in ovarian cancer treatment.[8]
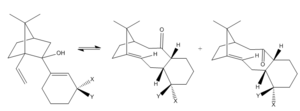
The medium sized rings within the two bicyclic compounds experience significant steric strain due to torsional and van der Waals interactions. The crowding of inner hydrogen atoms hinders the ring inversion and favours transannular reactions. The removal of two inner hydrogens by formation of an olefin reduces the strain and results in a stabilisation of the molecule.[9]
The olefin strain energy (OS), defined as the difference between the strained energy of an olefin and that of its parent hydrocarbon, can be used to interpret and to predict the stability and the reactivity of bridgehead olefins.[10]
Introduction of a double bond in normal or bridged medium rings brings about strain release hence the respective olefins have been named as hyperstable. The name reflects the increase of resonance energy rather than strain reduction in the system. The reactivity of hyperstable alkenes is similar to that of aromatic hydrocarbons which means that they do not undergo hydrogenation easily and are reactive towards electrophiles. In fact, they are reluctant to hydrogenation even under harsh catalytic conditions, although they can be reduced with diimide or epoxidised with peroxycarboxylic acid. Depending on the degree of OS, alkenes in normal or bridged medium-sized rings prefer substitution rather than addition reactions. Embedded in an enol, they do not reverse the keto-enol equilibrium as the carbonyl maintains one of the strain reducing sp2centres.[11]
Compounds 9 and 10 participate very slowly in hydrogenation reactions, however on standing one of the molecules isomerises to the other. Prolonged reaction times are characteristic features of thermodynamic control, where the most stable isomer is formed once the system is allowed to equilibrate for a long period of time at elevated temperatures. Inspection of MM2 and MMFF94 energies allows for a distinction between the kinetic and thermodynamic products of the oxy-Cope rearrangement, but also for identification of cyclohexyl ring conformers.
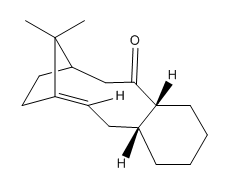
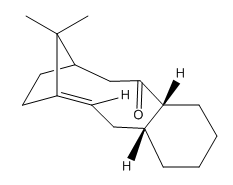
The cyclohexane ring adopts 2 conformations, chair and twist boat. The chain conformation is the global energy minimum on the energy profile diagram of cyclohexane as all the bonds are fully staggered. The twist boat conformer is not as low in energy as its chair form but it is lower than the true boat. The twist boat form is a local energy minimum. It can be summarised that cyclohexane has two stable conformers, the chair and the twist boat.[12] This is shown in Figure 5.
MM2 calculations are found in Table 3. The results suggest that in general, conformers of isomer 10 are lower in energy than their counterparts in 9. The chair conformation of 10 is thermodynamically more stable by 6 kJmol-1, whereas in the case of the twist boat conformer, the difference is 5.85 kJmol-1. In all cases, the major constituent of the total energy is the torsion, which makes up about 20 kJmol-1 of each value. The quest for the lowest energy conformation consisted of optimisation of sp2 and sp3 angles in the central medium ring as well as minimisation of van der Waals repulsive interactions by manually moving the atoms into more favourable orientations.
| Structure | Stretch | Bend | Stretch-Bend | Torsion | Van der Waals | Dipole-Dipole |
|---|---|---|---|---|---|---|
| Isomer 9 Chair | 2.63 | 13.97 | 0.35 | 20.98 | 13.94 | -1.58 |
| Isomer 9 Twist Boat | 2.88 | 17.27 | 0.47 | 20.61 | 14.38 | -1.71 |
| Isomer 10 Chair | 2.62 | 11.34 | 0.34 | 19.67 | 12.87 | -2.00 |
| Isomer 10 Twist Boat | 2.71 | 11.83 | 0.39 | 22.88 | 14.34 | -2.00 |
Substituents surrounding the sp3-sp3 bonds adopt several equivalent staggered conformations. Eclipsed alternatives occur as transition states or saddle points connecting the staggered structures. Torsional potentials are used to mimic the preference for staggered conformations about sp3-sp3 bonds.[13] The bond angle for a tetrahedral carbon is 109°28’ in methane and if this is a typical value for sp3 hybridised carbon in a ring, many of the planar structures must have significant distortion in the geometry of that ring. The greater the distortion from the ideal tetrahedral angle, the less stable the structure should be. The energy induced in a molecule due to this distortion is called Baeyer strain. However, a cyclic molecule such as cyclohexane does not exist in a planar conformation. It adopts the discussed chair conformation to avoid eclipsing interactions between the vicinal hydrogens. The strain energy arising from this is called torsional strain.[14]
Significant torsional strain is experienced by the hydrogenated atropoisomers of 9 and 10 because, as shown in Table 4, the CA-CB-CC bond angles deviate largely from the ideal tetrahedral angle. In the case of the non-hydrogenated structures, the olefin bond angles are similar to the ideal sp2 hybridised angles of 120°. The molecules are therefore extremely reluctant to undergo hydrogenation because of the increased experienced torsional strain between the A, B and C carbon atoms.
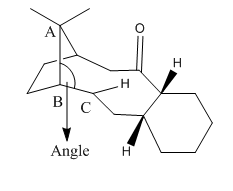
| Structure | CA-CB-CC Bond Angles [°] | |
| Actual | Optima | |
| Isomer 9 Chair | 120 | 120 |
| Hydrogenated Isomer 9 | 117 | 109 |
| Isomer 10 Chair | 123 | 120 |
| Hydrogenated Isomer 10 | 119 | 109 |
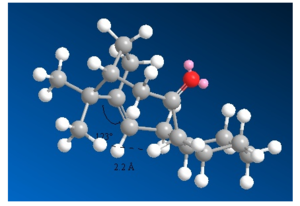
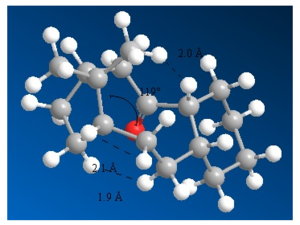
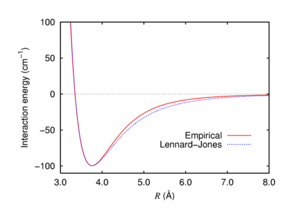
The second important factor in explaining the stability of isomers 9 and 10 with respect to hydrogenation are van der Waals interactions. Van der Waals forces are described by the Lennard-Jones potential, like the one in Figure 6. At short distances the function is strongly repulsive, but at longer distances it becomes attractive. For H-H distances smaller than 2.1 Å, the potential becomes increasingly repulsive. The repulsive and destabilising interactions between hydrogens are more significant in the alkane counterparts of 9 and 10.[15] The van der Waals interactions in the molecules are shown in Figures 7, 8 and 9.[16]
To conclude, isomers 9 and 10 react very slowly in hydrogenation reactions because on going from sp2 to sp3 hybridised centres, the molecule suffers increased torsional strain as well as van der Waals repulsive interactions. On standing molecules 9 will isomerise under thermodynamic control to yield the more stable structure 9.
In Table 5 data computed using the MMFF94 and MM2 methods are compared. Although the individual MM2 energies are about 20 kJmol-1bigger that those computed using Merck Molecular Force Field, the general trend is preserved. Isomer 10 has lower energy conformers than its atropoisomer 9. The differences are: for the chair conformation 5.77 kJmol-1 and 11.33 kJmol-1 for the twist boat.
| Structure | Energies [kcalmol-1] | |
| MM2 | MMFF94 | |
| Isomer 9 Chair | 48.7237 | 66.5774 |
| Isomer 9 Twist Boat | 53.0101 | 77.9043 |
| Isomer 10 Chair | 42.6839 | 60.5494 |
| Isomer 10 Twist Boat | 48.1582 | 66.3190 |
| Hydrogenated Isomer 9 (Chair) | 49.3014 | 71.1616 |
| Hydrogenated Isomer 10 (Chair) | 51.3565 | 71.4705 |
Regioseletive Addition of Dichlorocarbene

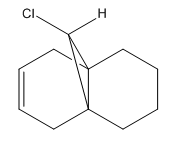
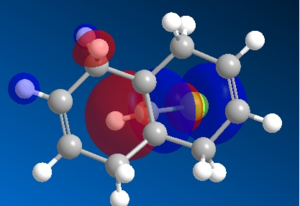
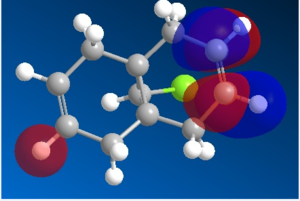
9-chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene participates in a regioselective electrophilic addition reaction of dichlorocarbene. There are two potential sites of attack: the exo and endo double bonds. Using molecular modelling tools such as MM2 and MOPAC, the molecule geometry was optimised and molecular orbitals were explored in order to indicate the more nucleophilic of the two alkenes.
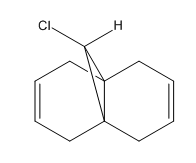
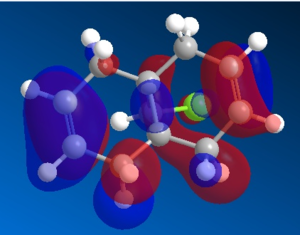
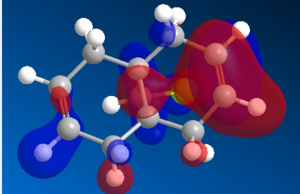
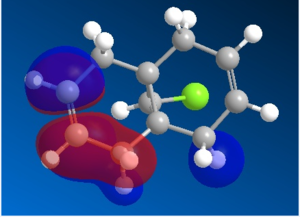
Organic reactions take place when the HOMO of a nucleophile overlaps with the LUMO of the electrophile and a new bond is formed. Two electrons from the HOMO orbital are donated into the empty LUMO. The reaction may initially be driven by electrostatic interactions of charges or dipoles but to obtain the complete picture of reactivity one must also consider the energy and orientation of the orbitals which overlap. The five generated molecular orbitals for 9-chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene are presented in Figure … The point group of the molecule is CS and this symmetry is also exhibited by the orbitals obtained.
| Structure | ||||
| MM2 Energies [kcalmol-1] | Dialkene | Monoalkene | Dialkene with -NO2 Group | Dialkene with -SiMe3 Group |
| Stretch | 0.6178 | 0.8383 | 0.7193 | 0.7059 |
| Bend | 4.7304 | 4.9018 | 6.1086 | 5.3806 |
| Stretch-Bend | 0.0399 | 0.0886 | 0.0623 | -0.0293 |
| Torsion | 7.6634 | 12.4914 | 7.7102 | 10.1782 |
| Non-1,4-VDW | -1.0664 | -1.115 | -0.4221 | -4.0055 |
| 1,4-VDW | 5.7972 | 7.5047 | 8.0490 | 5.2699 |
| Dipole/Dipole | 0.1124 | 0.0736 | -1.9616 | -0.1051 |
| Total Energy | 17.8945 | 24.7834 | 20.1581 | 17.3947 |
| PM6 Energy [kcalmol-1] | 19.7402 | -0.3628 | 12.2670 | 20.0506 |
Since HOMO is the most reactive orbital towards electrophiles like dichlorocarbene, inspection of its shape provides a lot of information about which olefin is attacked in preference. Inspection of electron density located on both of the alkenes it can be rationalised that endo alkene clearly shows a larger sterically accessible π-orbital area than the exo alkene. The endo orbital is more localised and hence higher in energy. Rzepa. Antiperiplanar overlap with the σ*C-Cl antibonding orbital LUMO +1 results in the exo π-orbital (HOMO -1) stabilisation by 0.08 eV relative to the endo π-orbital (HOMO). The σ*C-Cl orbital is low-lying because of the electronegative nature of the chlorine atom which makes it a good electron acceptor. The exo bond is therefore less nucleophilic and dichlorocarbene will not add across this alkene.
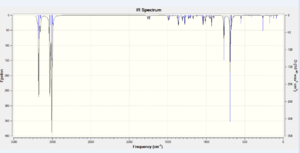
The mentioned σ*C-Cl and π-orbital interaction affects the length of C=C and C-Cl bonds. This is correlated with the bond order as when electrons are placed in an antibonding orbital, the bond order decreases which corresponds to the mentioned bonds becoming weaker and longer. This corresponds to the orbitals becoming more diffuse and delocalised. On hydrogenation of 9-chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene and removal of the exo C=C bond, there is no longer a possibility for LUMO +1 and HOMO -1 secondary orbital overlap. In theory this corresponds to strengthening and shortening of the remaining C=C endo and C-Cl bonds. The endo C=C stretching frequency should not be greatly affected by the loss of the exo olefin. The results are included in Table 7.
| IR Vibrational Assignment [cm-1] | |||
| Dialkene | Monoalkene | ||
| Peak | Vibration Description | Peak | Vibration Description |
| 770.80 | C-Cl stretch | 779.93 | C-Cl stretch |
| 1737.01 | C=C exo stretch | No C=C exo stretch | |
| 1757.43 | C=C endo stretch | 1753.76 | C=C endo stretch |
The theoretical approach is well correlated with computational results. In the dialkene molecule, the C=C endo bond should be stronger than the C=C exo bond. Since energy is directly proportional to frequency, the stronger the bond, the higher its vibrational frequency on an NMR spectrum. The C=C exo stretch frequency is almost 20 cm-1 lower than that for the endo alkene. On hydrogenation, the exo double bond is lost, hence the 1754 cm-1 stretch must correspond to the endo alkene. An increase of the C-Cl stretch frequency by about 10 cm-1 was also observed.
Considering bond lengths of C=C endo and C-Cl on removal of the C=C exo alkene, shortening of the bonds is a consequence of their strengthening. The bond lengths for C=C endo in dialkene and monoalkene are virtually the same whereas the C-Cl bond is elongated on hydrogenation. This is not consistent with the computational data obtained. Possible explanations for this could be incomplete geometry optimisation, software limitations and other stereoelectronic effects in operation.
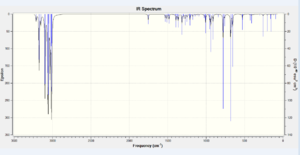
An optional study into substituted 9-chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene was undertaken. One hydride substituent on the exo alkene was substituted with either a strongly electron withdrawing NO2 group or with electron donating SiMe3. The computed IR stretches are presented in Table 8.





| IR Vibrational Assignment [cm-1] | |||
| Dialkene with -NO2 Group | Dialkene with -SiMe3 Group | ||
| Peak | Vibration Description | Peak | Vibration Description |
| 840.47 | C-Cl stretch | 764.11 | C-Cl stretch |
| 1737.79 | C=C exo stretch | 1707.49 | C=C exo stretch |
| 1755.35 | C=C endo stretch | 1737.25 | C=C endo stretch |
In the case of the nitro group, electron density is being pumped out of the alkene system into the σ* C-N antibonding orbital, weakening the double bond and shifting its vibrational frequencies to lower values. The exo π-orbital becomes an even more low-lying HOMO-1 in comparison to its unsubstituted conterpart. The overlap between itself and the σ* C-Cl antibonding orbital is less favourable because of the larger HOMO-1-LUMO+1 energy gap. The C-Cl bond should therefore be stronger than in the parent dialkene and consequently have a greater IR frequency. The difference is quite large and equals about 70 cm-1. The same trend is observed for the C=C endo stretch, however the difference is now less than 1 cm-1.
When 9-chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene was substituted with a trimethylsilyl group, the findings were exactly the opposite of those in the case of the electron withdrawing . The C-Cl bond becomes much weaker and this is reflected in the 6 cm-1 drop in the stretching frequency in comparison with the unsubstituted dialkene. The C=C exo bond is lowered by about 30 cm-1. The reason for these shifts is the electron donating nature of the silyl group. The susbstituted exo π-orbital becomes a high-lying HOMO-1 and the energy approaches the energy of the σ* C-Cl LUMO+1 orbital. The energy gap is now much smaller and the secondary overlap is much more favourable.

Monosaccharide Chemistry: Glycosidation
The Fischer glycosylation deals with acid-catalysed reaction with an unprotected hemiacetal donor. The reaction is under thermodynamic control and an excess of glycosyl acceptor alcohol is needed to drive the equilibrium to glycoside. The method is best employed with simple alcohols solvents. In addition, the typical reaction requires high temperatures and long reaction times which may destroy the sensitive substrates. Anomeric sensitivity in the glycosylation process is usually dictated by the relative ground state energies of the product glycoside anomers.
Fischer glycosylation involves protonation of the cyclic hemiacetal – the free sugar – followed by its reaction with an alcohol to form the respective cyclic acetal. Protonation of the anomeric group is followed by departure of water from the saccharide in the spirit of SN1 mechanism. This leads to a cationic intermediate, a resonance-stabilised oxocarbenium ion. Reaction with an alcohol molecule yields the desired glycoside. As it is equilibrium reaction and water is the by-product, acetal hydrolysis shifts the equilibrium towards the starting material.
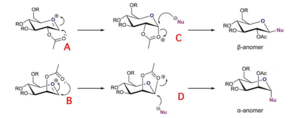
Fischer glycosylation gives a mixture of stereoisomeric glycosides. The pyranoside which is favoured by the anomeric effect is obtained as the main product since the reaction is under thermodynamic control. It can be crystallised from the mixture.
It is possible to control the stereochemistry of the newly formed anomeric bond. It is occasionally found with certain substrates that the rate of reaction is greater than expected and the configuration at the chiral carbon is retained and not inverted or racemized. In these cases there is usually a group with an unshared pair of electrons β to the leaving group. The mechanism operating in such cases is the neighbouring group mechanism. A carboxylic ester such as an acetate group can participate in the Fischer glycosylation. After the leaving group expulsion from the molecule, the carbonyl oxygen stabilises the intermediate glycosyl cation by cyclisation. The cyclic oxonium ion is opened in an SN2 manner by a nucleophile, which displaces the neighbouring group by a backside attach. This step brings about an inversion of configuration. The newly formed anomeric linkage is necessarily trans to the 2-hydroxy group. The gluco material forms specifically the β-glucoside whereas the manno starting material has the epimeric hydroxyl group at the α-position and is therefore the α-isomer. This is illustrated in Figure… March’s Advanced Organic Chemistry, 2001, 404 and Carbohydrate Chemistry Primer.
The two presented mechanisms have been investigated with the use of MM2 and MOPAC/MM6 computational methods. The methyl group was chosen for calculations as it is a compromise between the hydroxyl group which are avoided in the model because of the hydrogen bonding interactions and more sterically demanding higher alkyl substituents or acetyl groups. These would impose a heavier computational demand and longer calculation times. MM2 energies and MOPAC/MM6 heats of formation of the oxonium cation rings A and B as well as their ring flipped counterparts are presented in Table 9. The conformers differ in the acyl group pointing either above or below the plane of the oxonium ion.
| Structures | ||||
| MM2 Energies [kcalmol-1] | A | A' | B | B' |
| Stretch | 2.8801 | 2.5822 | 2.9948 | 2.5919 |
| Bend | 11.4967 | 10.4017 | 13.8673 | 10.4383 |
| Stretch-Bend | 1.0502 | 0.9175 | 1.1638 | 0.8147 |
| Torsion | 1.4522 | 3.5297 | 2.0564 | 1.1282 |
| Non-1,4-VDW | 2.0992 | -0.6702 | 0.7996 | -0.8409 |
| 1,4-VDW | 18.4277 | 19.2887 | 18.6683 | 19.4979 |
| Charge/Dipole | -24.1669 | -6.7310 | -12.935 | -12.7101 |
| Dipole/Dipole | 7.6744 | 4.5462 | 4.1653 | 5.9748 |
| Total Energy | 20.9137 | 33.8648 | 30.7805 | 25.8947 |
| PM6 Energy [kcalmol-1] | -91.6520 | -77.5061 | -85.9500 | -68.6109 |
In structure A, the acetyl group is pointing below the plane of the oxonium cation and the attack occurs from the bottom face of the molecule, leading to the nucleophile opening the cyclic intermediate from the top face. Using MOPAC, it was found that the heats of formation of A and C are equal in magnitude, -91.65 kcalmol-1. In sugar B, the acetyl group is located above the oxonium cation and its attacks from the top side allowing the incoming nucleophile to approach from the bottom. Very similar heats of formation are also observed for structures B and D, -85.95 kcalmol-1 and -88.72 kcalmol-1, respectively. This can be explained by noticing that the true structure is a hybrid of A and C as well as B and D and lies somewhere in between. PM6 treats the molecule as one unit and moves electron charges in the molecule to localise them in the lowest energy conformation possible.
Unlike in structures A and B, A’ and B’ are the ring flipped conformers of A and B, where the acyl group is now pointing below the plane of the oxonium cation. On comparison of the heats of formation between A and A’ one notices that the former is more energetically stable by about 14 kcalmol-1. The same trend is observed for the B-B’ pair, the difference in energy now being 17 kcalmol-1.
Structure A: Molecule A |
Structure A: Molecule A’ |
Structure B: Molecule B. |
Structure B: Molecule B’ |
Considering structures C, D and their ring flipped equivalents, the following observations can be noted. Molecule C is about 20 kcalmol-1 more stable than C’ and for D and D’, the difference is about 22 kcalmol-1. They are not formed because the interconversion barrier is too high and any rotation will lead to a more stable conformation. The detailed results can be found in Table 10.
Structure C: Molecule C. |
Structure C: Molecule C’. |
Structure D: Molecule D. |
Structure D. Molecule D’. |
| Structures | ||||
| MM2 Energies [kcalmol-1] | C | C' | D | D' |
| Stretch | 2.1441 | 3.1216 | 1.9645 | 2.6053 |
| Bend | 14.7973 | 16.6298 | 19.1204 | 16.8425 |
| Stretch-Bend | 0.8142 | 0.8305 | 0.7835 | 0.7112 |
| Torsion | 8.8735 | 12.1146 | 9.6138 | 6.8274 |
| Non-1,4-VDW | -2.2477 | -3.1902 | -3.8643 | -2.9049 |
| 1,4-VDW | 17.275 | 20.8831 | 17.5477 | 19.2261 |
| Charge/Dipole | -7.3249 | 3.1895 | -3.2087 | 1.3908 |
| Dipole/Dipole | -1.8805 | -0.7772 | -1.7719 | -0.8527 |
| Total Energy | 32.4511 | 52.8017 | 40.185 | 43.8457 |
| PM6 Energy [kcalmol-1] | -91.6502 | -66.7240 | -88.7273 | -66.6731 |
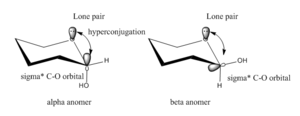
The equatorially positioned substituents of carbohydrate rings are, for steric reasons, more energetically stable that their axial counterparts. However, for molecules like C and D with electronegative groups at the anomeric centre, the anomeric α-configured derivatives with the anomeric group positioned in the axial positions are often more stable than their equatorial equivalents due to the anomeric effect. It partly involves a dipole-dipole effect based on intramolecular electrostatic interactions of two dipoles next to the anomeric centre. The anomeric effect is most importantly, however, a stereoelectronic effect. A lone pair of electrons located on the anomeric oxygen overlaps with the antibonding σ*-orbital of the C-O bond of the cyclic oxonium ion. This favourable negative hyperconjugation is only possible when the C-O bond is axial. If the C-O bond is equatorial, the nonbonding electrons of the endocyclic oxygen are delocalised into the σ*C-H orbital which is much higher in energy than the σ*C-O orbital. The overlap of the lone pair is therefore more efficient in the α-anomer than in the β-anomer. Essentials of Carbohydrate Chemistry and Biochemistry.
The distribution of particles over a series of energy levels can be found by using the Boltzmann distribution. It gives the probability of a particle occupying a given energy level is proportional to the exponential of the negative of its internal energy divided by Boltzmann’s constant and the absolute temperature in K. Seddon’s Thermodynamics Book. The ratios of C’/C and D’/D are … and … respectively.
The reason for the formation of both exclusively β-anomers from A and α-anomers from B is the neighbouring group participation. The 2-acetyl group stabilises the oxonium ion blocking one face of attack and forcing the incoming nucleophile to attack the opposite face stereospecifically. Such high selectivity can only be obtained if the participating ester group is in a 1,2-trans relationship to the desired glycosidic substituent. Ed Tate’s notes.
MOPAC is semi-empirical molecular orbital package for the study of solid state and molecular structures and reactions. The semi-empirical Hamiltonian PM6 is used in the electronic part of the calculation to obtain molecular orbitals, the heat of formation and its derivative with respect to molecular geometry. Using these results MOPAC calculates the vibrational spectra, thermodynamic quantities, isotopic substitution effects and force constants for molecules, radicals, ions, and polymers. http://openmopac.net/manual/index.html In addition, PM6 takes into consideration secondary orbital overlaps. MM2 is a less powerful method as it does not use a wave function or total electron density. The energy expression is a simple algebraic equation for the energy of a compound and the input data are obtained from spectroscopic experiments or ab initio methods. P 49 David Young, Computational Chemistry For systems where good parameters are available, it is possible to make very good predictions of geometries and relative energies of a large number of molecules. The main limitation of the method is the lack of good parameters for molecules slightly out of the ordinary. In addition, since molecules are described by a ‘’ball and spring’’ model, it is not possible to analyse the electron distribution and handling of charged molecules may lead to increasingly inaccurate results. In the case of sugars and especially the oxonium ions, PM6 energies are thought to be much more accurate and therefore only those were investigated. p. 23, 69-70, Frank Jensen, Introduction to Computation Chemistry.
Mini Project: Hetero Diels-Alder
Computational chemistry has made significant contributions to chemical research in the past decades and is becoming a common tool in many areas of research. The following computational experiment is used to explain experimental results regarding the products formed during a hetero Diels-Alder cycloaddition reaction between cyclopentadiene and glyoxylic acid in water, published by Lubineau et al. This is an illustration of the acceleration of organic reactions in aqueous media. The hydrophobic effect was suggested as the phenomenon responsible for this acceleration and the interpretation was extended to the reactions exhibiting a negative volume of activation. The hetero Diels-Alder reaction is known to increase in rate under pressure, implying a negative volume of activation. The reaction is facilitated in water.
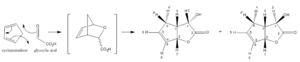
The mechanism of the reaction is consistent with a [4+2] hetero Diels-Alder reaction (Figure 1) followed by an intramolecular rearrangement (Figure 2). The endo intermediate gives rise to the major lactone 1 whereas the minor lactone 2 is derived from the exo intermediate.

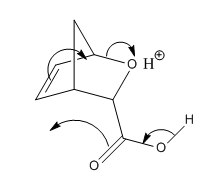
A common issue in computational chemistry is the choice of whether to simplify a molecule by removing bulky substituents. Although such simplifications introduce error into the results by neglecting the steric and electronic effects of the substituents, the smaller models permit the use of more accurate theoretical methods. The lack of bulky substituents on either lactone makes calculations not only faster but relatively more accurate.
The reaction of cyclopentadiene (0.22 M) with an aqueous solution of glyoxylic acid (2.25 M) at different pH with vigorous stirring gave the following yields and selectivities as outlined in Table 11.
| pH | Time [h] | Temperature [°C] | Yield [%] | 1:2 ratio |
| 6 | 24 | 60 | 16 | 60:40 |
| 2.5 | 7.5 | 40 | 72 | 60:40 |
| 0.9 | 1.5 | 40 | 83 | 73:27 |
The goal of establishing those factors that control the regiochemistry and stereochemistry of reaction has challenged the organic chemist for many years. The majority of general organic texts present the Diels-Alder reaction as favouring endo products. In most cases the exo product is the thermodynamically most stable but the endo adduct forms much more rapidly and is therefore referred to as the kinetic product. Woodward and Hoffmann proposed secondary orbital overlap (SOO) as a molecular orbital based explanation of the observed endo stereo-preference in the Diels-Alder reaction.
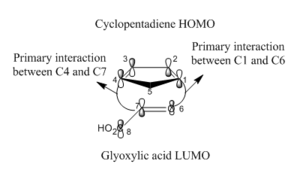
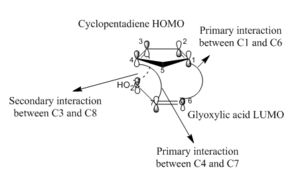
SOO is defined as the positive overlap of a nonactive frame in the frontier MOs of a pericyclic reaction. In the presented hetero Diels-Alder of cyclopentadiene and glyoxylic acid, the primary interactions involve carbons 1-6 and 4-7 and define the active frame where bonds are formed or broken. Carbons 3 and 8 are involved in a secondary interaction since no bond changes are encountered at these sites. These carbon atoms interact strongly in the endo transition state but not at all in the exo transition state. Irrespective of whether the HOMO of the diene interacts with the LUMO of the dienophile or the diene LUMO interacts with the dienophile HOMO, orbital phasing at both the primary and secondary centres predicts a stabilising interaction. SOO hence preferentially facilitates formation of the endo transition state rather than the exo TS where such an interaction is absent. The isolation of the kinetic product is also in part owing to the highly exergonic nature of the reaction. The Hammond postulate predicts that a comparable but more energetically neutral reaction has a later transition state (occurs in the product channel) and has its energy comparable to that of the products.
Lactone 1. |
Lactone 2. |
IR, 13C and 1H NMR spectra and J coupling constants for the latter were computed using Gaussian. In addition, computational measurements of optical rotation and free energy of formation were investigated. Using those analytical tools, lactones 1 and 2 were distinguished from each other. The numbering system of carbon and hydrogen atoms is included in Figure …


13C NMR data, in Table 12, is in reasonable agreement with experimental findings of Augé and Lubin-Germain, obtained on an unspecified 62.5 MHz machine with d-chloroform as solvent. The difference between the individual shifts does not exceed 4 ppm in any case. Peaks for Lactone 2 are generally shifted further downfield in comparison with Lactone 1. The carbonyl carbon is the most deshielded atom in the spectrum because of the electronegative nature of the oxygen atom. The most shielded carbon atom in both molecules is the only stereogenic centre of the molecule. In the endo intermediate derived product, the hydrogen atom is pointing towards the observer and finds itself rather in between the electronegative hydroxyl and carbonyl oxygens. It will experience a little more enhanced shielding effect and its peak will be shifted higher upfield relative to that of Lactone 2, experiencing a somewhat relatively reduced influence of the carbonyl.
| 13C NMR Chemical Shift Assignment [ppm] | |||||
| Lactone 1 | Lactone 2 | ||||
| Experimental* | Theoretical** | Carbon Assignment | Experimental* | Theoretical** | Carbon Assignment |
| 30.80 | 32.98 | C6 | 36.64 | 37.75 | C6 |
| 40.52 | 42.65 | C1 | 44.14 | 47.02 | C1 |
| 69.19 | 68.61 | C5 | 74.37 | 73.38 | C5 |
| 86.58 | 85.61 | C2 | 87.48 | 86.23 | C2 |
| 127.50 | 125.67 | C8 | 129.33 | 128.15 | C8 |
| 141.16 | 140.27 | C7 | 136.75 | 135.47 | C7 |
| 177.97 | 173.80 | C4 | 177.67 | 174.36 | C4 |


The experimental proton NMR spectrum was obtained from an unspecified 250 MHz spectrometer with deuterated chloroform as solvent. It in reasonable agreement with the experimental data and the shift displacement is never larger than 1 ppm. The most deshielded protons (excluding the OH hydride) are the alkene protons with a chemical shift in the region of 5-6 ppm. The most shielded protons are the methylene protons H4 and H4’. The slight differences arise from the fact that in a practical experiment, the chemical shift is affected by factors like solvent, temperature or proton exchange. The peaks may coalesce because of similar chemical shifts and it is not always possible to distinguish couplings to neighbouring protons. Since only one molecule is being modelled using the computational technique employed, interactions with the environment have been neglected and it is much easier to identify individual peaks. For detailed assignment refer to Table 13.
| 1H NMR Chemical Shift Assignment [ppm] | |||||
| Lactone 1 | Lactone 2 | ||||
| Experimental* | Theoretical** | Proton Assignment | Experimental* | Theoretical** | Proton Assignment |
| 6.27 | 6.59 | H5 | 6.10 | 6.37 | H5 |
| 5.94 | 6.25 | H6 | 5.91 | 6.24 | H6 |
| 5.35 | 5.36 | H7 | 5.55 | 5.61 | H7 |
| 4.75 | 4.46 | H2 | 4.17 | 4.01 | H2 |
| 3.23 | 3.06 | H3 | 3.06 | 2.86 | H3 |
| 2.77 | 2.91 | H4' | 2.77 | 2.74 | H4' |
| 2.47 | 2.37 | H4 | 2.58 | 2.65 | H4 |
Similar arguments apply to the computed IR spectra (Table 14). Since only one molecule was modelled, there is a striking difference in the appearance of the OH peak. The broad band due to hydrogen bonding in the system is replaced by a narrow and small intensity peak in the computed spectrum at about 3800 cm-1. The C=O lactone peak the only one assigned by Augé has a 100 cm-1 lower frequency that the theoretical one. A possible explanation for this is the presence of overtone and combination bands in the experimental spectra as well as an oversimplified approach to calculations. Fortunately for chemists, the frequencies can be brought into a reasonable agreement with the experiment by multiplication by a relevant correction factor. The same approach can be used in correcting IR intensities.
| IR Vibrational Assignment [cm-1] | |||||
| Lactone 1 | Lactone 2 | ||||
| Experimental* | Theoretical | Vibration description | Experimental* | Theoretical | Vibration description |
| 1745 | 1862 | C=O lactone | 1780 | 1870 | C=O lactone |
| n/a | 3792 | O-H free | n/a | 3743 | O-H free |
| n/a | 3113 | C-H alkene | n/a | 3113 | C-H alkene |
| n/a | 3085 | n/a | 3074 | ||
| n/a | 3057 | n/a | 3039 | ||
| n/a | 2967 | C-H alkane | n/a | 2964 | C-H alkane |
| n/a | 1211 | C-O lactone | n/a | 1202 | C-O lactone |
| n/a | 1159 | C-O lactone | n/a | 1140 | C-O lactone |
| n/a | 1001 | C-H alkene bend | n/a | 1011 | C-H alkene bend |

Computational Chemistry: Introduction to the Theory and Applications of ...By Errol G. Lewars
In the computational spectra, one clearly identifies the weak C-H alkene and alkane stretches in the region of 2900-3100 cm-1 as well as a C-O lactone stretch at around 1200 cm-1. Despite the reasonable agreement of the theoretical and experimental spectra, IR spectroscopy does not allow for distinguishing between the two stereoisomers.
Most probably the best tool for identification of the isomers (here only) is performing a J coupling analysis. Gaussian was used to obtain all the coupling constants as it is a much more powerful software for such calculations, giving more accurate results than Janocchio which uses the Karplus equation and dihedral angles. The presence of electronegative substituents, hybridisation as well as bond properties affect the Karplus calculations in a significant way and produce rather inaccurate results. Gaussian computed coupling constants are presented in Table 15. In general, they correlate rather well with the journal findings.
| 1H NMR Coupling Constants [Hz] | |||||
| Lactone 1 | Lactone 2 | ||||
| Experimental | Theoretical | Protons | Experimental | Theoretical | Protons |
| 5.5 | 6.4 | J5,6 | 5.5 | 6.6 | J5,6 |
| 2.2 | 2.7 | J6,7 | 2.0 | 2.4 | J6,7 |
| 6.5 | 6.5 | J3,7 | 7.5 | 7.7 | J3,7 |
| 9.5 | 9.6 | J2,3 | 7.5 | 6.8 | J2,3 |
| 9.5 | 9.1 | J3,4 | 7.5 | 6.9 | J3,4 |
| 6.0 | 4.7 | J3,4' | 2.0 | 2.0 | J3,4' |
| 18* | 23.0 | J4,4' | 17.5* | 21.0 | J4,4' |
| 2.2 | 3.2 | J4',5 | 4.5 | 3.5 | J4',5 |
| 2.2 | 3.6 | J4,5 | 2.0 | 3.0 | J4,5 |
The main difference between the NMR spectra of the two isomeric lactones involves the coupling constants of H2. The proton is expected to couple with H3 with 3JHH coupling. In the case of lactone 1, the experimental doublet at 4.75 ppm couples with H3 with J = 9.5 Hz. The computed coupling of 9.6 Hz is hence in excellent agreement with literature data. For lactone 2, the experimental J coupling is 7.5 Hz while the Gaussian coupling is 6.8 Hz. There is a slight discrepancy between the results but a general trend is preserved. H2 of Lactone 1 has couples more strongly to H3 than that of Lactone 2 because of the stereochemistry. This method allows to distinguish between the isomers most efficiently.
In order to obtain a complete analysis of the structures, a 2-D NMR spectrum is required. A NOESY spectrum of both compounds would allow for the most accurate evaluation of the H2-H3 interactions. The authors observed that in the phase sensitive NOESY spectrum of lactone 2 there is clearly a coupling interaction between protons H2 and H4 whereas in the case of its isomer there is a correlation between H2 and H7 which is easily understood by considering the relative orientation of the hydrogens of interest.
A very interesting way for the distinction of enantiomers is performing an NMR spectrum with a chiral alignment medium. In this case, the molecule is partially aligned and anisotropic NMR parameters like residual quadrupolar couplings, residual dipolar couplings and residual chemical shift anisotropy can be measured. As the orientation in a chiral alignment medium is different for the two enantiomers, resulting anisotropic parameters differ as well and the determination of enantiomeric purity is possible. Paper just downloaded
The last laboratory technique discussed in this section is the optical rotation. Lactone 1 exhibits an optical rotation of -57.51° whereas in the case of its isomer the value is very similar in magnitude -60.45°. Since no experimental data was found, no comparison with literature can be made. Optical rotation measurements are conformation correlated hence even a small change in the molecule structure can have a huge impact on the value. Optical rotation of compounds with a magnitude greater than 100° can be predicted with higher confidence.
The last point of the analysis is determination of relative stability of lactones 1 and 2. PM6 computed heats of formation indicate that lactone 2 is more thermodynamically stable, by about 2 kcalmol-1. It originates from the exo adduct intermediate which is the thermodynamic product of the reaction. Augé found that the ratio of 1:2 formation is, under the conditions employed and outlined in Table 16 is always in favour of 1. At lower temperatures and shorter reaction times (kinetic control) there is a higher selectivity in favour of 1 (73:27) supporting the observation that 1 is the kinetic product of the reaction because of the favourable SOO effect in the endo intermediate.
| Structure | Energies [kcal/mol] | |
| MM2 | MOPAC | |
| Lactone 1 | 14.0297 | -107.9311 |
| Lactone 2 | 14.0555 | -109.4884 |
- ↑ Professor Henry Rzepa, 2nd Year Conformational Analysis Lecture Notes, 2011. http://www.ch.ic.ac.uk/local/organic/conf/
- ↑ Schmart, I. M.; Knot-Tso M. E. J. Chem. Educ., 2004, 81, 1633-36.
- ↑ Clayden, J.; Greeves, N.; Warren, S.; Wothers, P.; ‘Organic Chemistry’, 1st Ed., Oxford University Press, 2001, pp 235.
- ↑ http://pharmaxchange.info/press/2011/03/thermodynamic-product-vs-kinetic-product-with-examples/
- ↑ Baldwin, J. E.; J. Org. Chem., 1966, 31, 2441-2444. DOI:10.1021/jo01346a003
- ↑ Clayden, J.; Greeves, N.; Warren, S.; Wothers, P.; ‘Organic Chemistry’, 1st Ed., Oxford University Press, 2001, pp 912-915.
- ↑ Clayden, J.; Moran, W. J.; Edwards, P. J.; LaPlante, S. R.; Angew. Chem. Int. Ed., 2009, 48, 6398-6401. http://onlinelibrary.wiley.com/doi/10.1002/anie.200901719/pdf
- ↑ Paquette, L.; Elmore, S. W.; Tetrahedron Letters, 1991, 319-322. DOI:10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0
- ↑ Grimme W.; Bertsch, A.; Flock, H.; Noack, T.; Krauthäuse, S.; Cheminform Abstract, 1999, 30. DOI: 10.1002/chin.199902316
- ↑ Maier, W. F.; Schleyer, P.; J. Am. Chem. Soc., 1981, 103, 1891-1900 DOI:10.1021/jo00356a016
- ↑ Grimme W.; Bertsch, A.; Flock, H.; Noack, T.; Krauthäuse, S.; Cheminform Abstract, 1999, 30. DOI: 10.1002/chin.199902316
- ↑ Clayden, J.; Greeves, N.; Warren, S.; Wothers, P.; ‘Organic Chemistry’, 1st Ed., Oxford University Press, 2001, pp 455-459.
- ↑ Rappé, A. K.; Casewit, C. J.;‘ Molecular Mechanics Across Chemistry’, University Science Books, 1997, pp 8.
- ↑ Smith, M.;‘Organic Chemistry: An Acid-Base Approach’, CRC Press, 2011, pp 318-326.
- ↑ Professor Henry Rzepa, 2nd Year Conformational Analysis Lecture Notes, 2011. http://www.ch.ic.ac.uk/local/organic/conf/
- ↑ http://www.stanford.edu/group/pandegroup/folding/education/molmodel.html

