Mrd:gm1616

H + H₂ system

Dynamics from the transition state region

At the transition state, the PE surface has a gradient of 0 and it is a maximum point on the minimum energy pathway. A reaction must pass through this point to form products.

The minima of the potential energy surface changes value as the collision occurs, and the maximum point of this minimum PE path is the transition state. There is a the largest curvature along the minimum PE path at the TS, so if a small change in the reactions conditions occurs that favours either reactants or products, the point along the minimum energy pathway will quickly fall and the newly favoured molecule will form. At a minima, the potential energy will increase with any change in reaction conditions or change in the reactant/product molecule's geometry.

(This is ok. Would have been better to see mention of partial derivatives and how their values relate to different types of stationary points. Fjs113 (talk) 19:28, 14 May 2018 (BST))

Trajectories from r1 = r2: locating the transition state

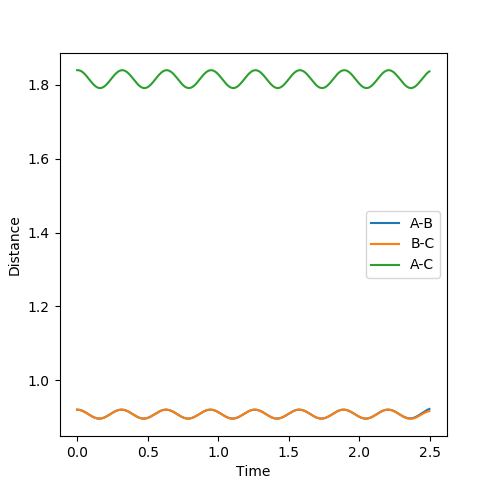
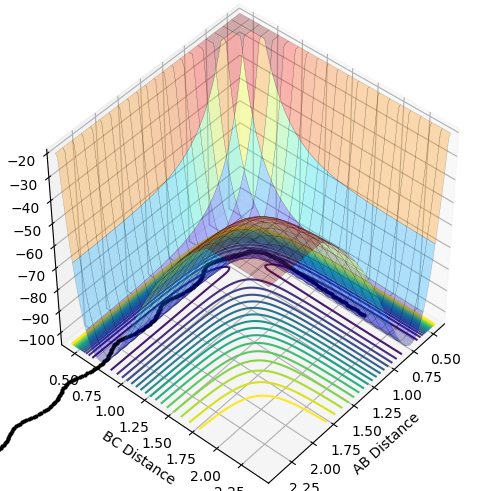
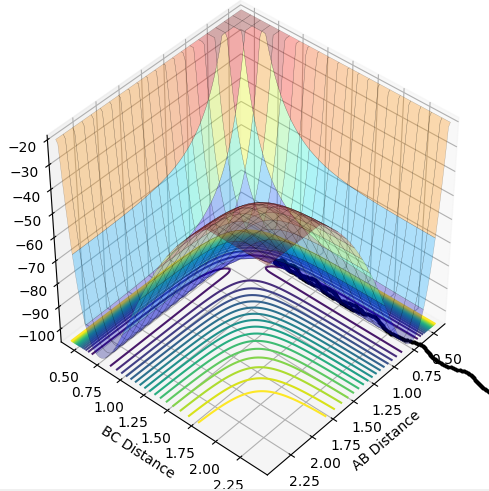
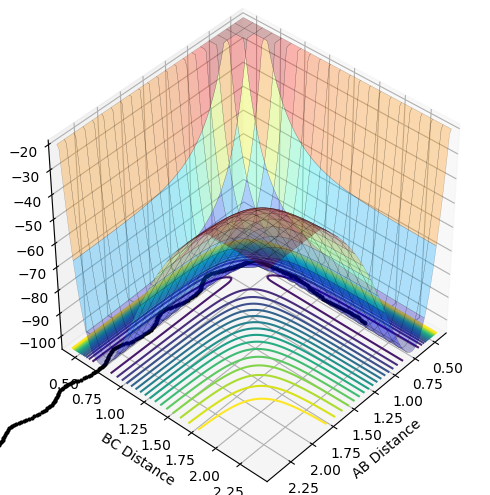
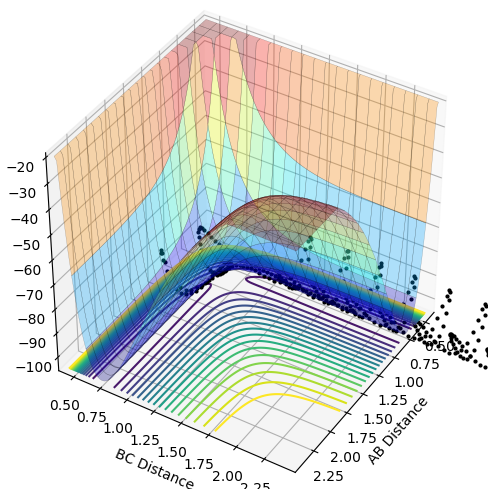
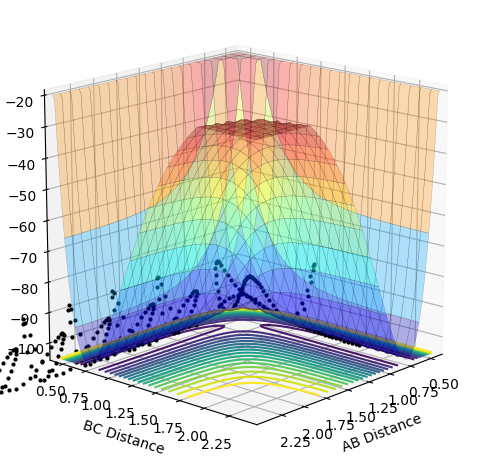
The best estimate for the transition state position is with the distance of AB=BC=0.9212 (4dp) because at this geometry the TS remains oscillating in the well only of the minimum energy pathway and has no gradient. This transition state can be seen below with the inter-nuclear distance-time graph which shows that the A-B and A-C are oscillating in phase, so A-B must also be oscillating in phase. This means that atoms A and C are vibrating periodically and in opposing directions around central atom B, so the system is not tending towards products or reactants.

(This is unfortunately not correct. At the TS, no vibrations should occur. Since the TS is an unstable stationary point, if the initial conditions are set to the TS with 0 momenta, the system should stay completely still. Fjs113 (talk) 19:28, 14 May 2018 (BST))

Calculating the reaction path

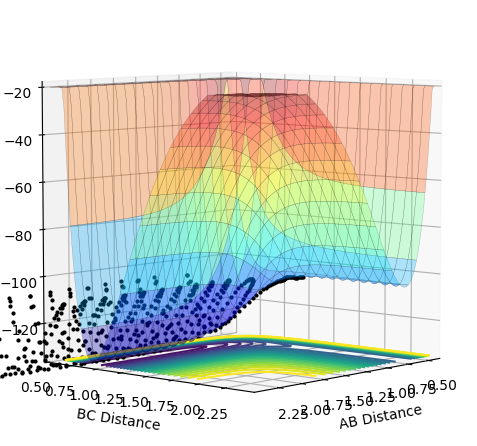
The differences between the MEP and dynamics calculation types on the PE surface plot are that there is no oscillating bond length in the MEP plot. Also, the MEP plot does not reach as large a bond length for the same amount of steps as the dynamic calculation type.

(These are correct observations. But why is this the case? You need to provide more explanation and maybe a picture or two for evidence. Fjs113 (talk) 19:28, 14 May 2018 (BST))

r1(t) = 0.5, r2(t) = 8.75, p1(t) = 1.1, p2(t) = 2.4.

r1(t) = 8.75, r2(t) = 0.5, p1(t) = 2.4, p2(t) = 1.1.

In the calculation where the final distances were set to the initial distances and the momenta were added with a negative sign, it could be seen that the final distances were much closer together, suggesting the system came back to the transition state conditions and neither reactants nor products predominated as the reaction proceeded. The final momenta was of the same magnitude but with a positive sign.

Reactive and unreactive trajectories

p1	p2	Total Energy (kJ/mol)	Reactive?	Potential Energy Surface Plot	Description of trajectory
-1.25	-2.5	-99.018	Yes		Initially, B-C's bond length oscillates and A-B's bond length decreases up until the transition state at which the reaction occurs and A-B's bond length oscillates and C-B's bond length increases.
-1.5	-2.0	-100.456	No		The A-B bond oscillates as it vibrates and the B-C bond length decreases as C approaches AB but the transition state is never reached and the molecule remains unchanged and C moves away from AB.
-1.5	-2.5	-98.956	Yes		Initially, B-C's bond length oscillates and A-B's bond length decreases up until the transition state at which the reaction occurs and A-B's bond length oscillates and C-B's bond length increases.
-2.5	-5.0	-84.956	Yes		The barrier is recrossed so that the C-B bond is formed briefly after the transition state before the A-B bond reforms and the C-B bond distance increases as it move away from the A-B molecule that has an oscillating bond length. There is greater overall energy in the system and the vibrations are much larger in the final molecules.
-2.5	-5.2	-83.416	Yes		The barrier is recrossed so that the A-B bond is formed briefly after the transition state before the B-C bond reforms and the A-B bond distance increases once again as B-C's bond distance oscillates about a fixed length as it vibrates. There is greater overall energy in the system and the vibrations are much larger in the final molecules.

(Are you sure that case 4 is reactive? Otherwise good. Fjs113 (talk) 19:28, 14 May 2018 (BST))

Transition state theory assumes that during a reaction, a quasi-equilibrium will be set up between the reactants and activated complexes in the transition state and the rate of reaction can be determined by the gradients and shape of the molecular potential profile that a moloecule follows as it crosses through the transition state . It assumes only classical behaviour of the molecules. The theory is good at predicting rates for generic reaction trajectories at high temperatures (since classical mechanics deviates less from quantum mechanics), but it assumes that the product state remains unchanged indefinitely and so it cannot be accurate for the barrier crossing trajectories since the product state exists temporarily for those conditions. Also, it does not take into account the concentration/surface area which can affect a reaction rate significantly.

EXERCISE 2: F - H - H system

PES inspection

The total energy for H₂ + F is -98.5 kJ/mol (20.5 kJ/mol kinetic and -119.0 kJ/mol potential) when HH distance = 0.74, HF distance = 2, p_(HH)=2 and p_(FH)=-0.5. The total energy for H-F + H is -78.0 kJ/mol (31.0 kJ/mol kinetic and -109.0 kJ/mol potential) when HH distance = 1, HF distance = 1.5, p_(HH)=2 and p_(FH)=-3. This shows that the H₂ + F is the exothermic process and the reverse reaction is endothermic. The H-H bond strength is 432 kJ/mol and the H-F bond strength is 565 kJ/mol so the H-F bond is stronger by 133 kJ/mol and hence the reaction which breaks the H-F bond will be unfavourable since the energy required to break the bond is not regained by the H-H bond formation.

(Good. Would have been even better with a picture, e.g. a surface plot or an MEP energy vs time plot showing the difference in potential energy. Fjs113 (talk) 19:28, 14 May 2018 (BST))

The approximate transition state was when the atoms has a bond length of 1.58 for H-F and 0.76 for H-H at which point the H atom in between the H and F atoms oscillated periodically between the H-F bond and the H-H bond. For this asymmetric system, it is expected that the distance between all 3 atoms is not equal. The transition state is closer in energy to H₂ + F and so, according to Hammond's Postulate, this suggests the transition state has a geometry which is similar to these reactants too. Energy of the transition state is -104.5 kJ/mol (12.5 kJ/mol kinetic and -117 kJ/mol potential).

(As above, this is unfortunately not the TS. Fjs113 (talk) 19:28, 14 May 2018 (BST))

The difference between the energy of the transition state and the energy of the reactant molecules gives the activation energy:

Activation Energy of H₂ + F = -98.5 - (-104.5) = 6 kJ/mol

Activation Energy of H-F + H = -78.0 - (-104.5) = 26.5 kJ/mol

The difference in these activation energies proves that when H₂ + F is the forward reaction, the reaction is exothermic since H₂ + F has a higher energy than the H-F + H products, and so ΔH_reaction = - 20.5 kJ/mol.

(Again, this could be illustrated better. Fjs113 (talk) 19:28, 14 May 2018 (BST))

Reaction dynamics

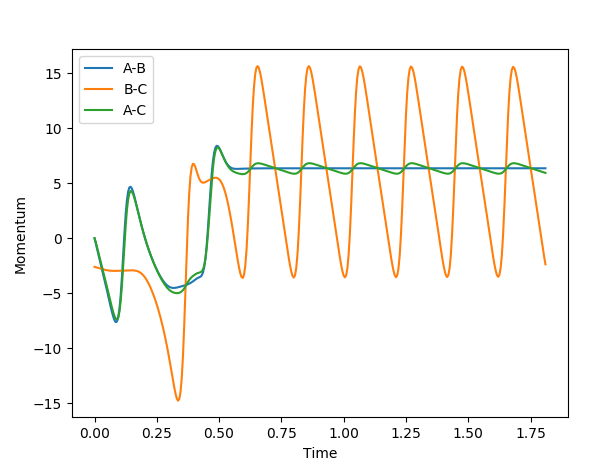
In the reaction trajectory between F and H₂, the reaction barrier is crossed three times as the F + H₂ reforms and then H-F + H remains as the final product. This can be seen in the inter-nuclear momenta vs time graph below which shows the system being crossed when t=0.33, 0.42 and 0.57, of which the crossing at 0.33 and 0.57 correspond to the H-F bond forming and the H-F inter-nuclear momenta at these points increases to a displacement of 9 as the molecule vibrates periodically. Initially, the system has mainly kinetic energy as the H-H bond approaches the stationary F atom until the first H atom is closer to F than the equilibrium bond distance, at which point the nuclei from the atoms repel each other and most of the kinetic energy is converted to potential energy as the H atom is now stationary. However, as the H-F bond lengthens under the nuclei's repulsion, the second H atom is still approaching the first H atom until they reach the minimum separation distance and begin to repel. This repulsion moves the first H atom back towards the F atom and so the H-F bond reforms and the second H atom moves away from the H-F molecule as the potential energy it gained in the repulsion at the minimum separation distance is converted into kinetic energy. Throughout the reaction, the total energy never changes but its composition of kinetic energy and potential energy does change.

This could be proven experimentally by using heavier Deuterium to replace one of the hydrogens and then determining whether there is a change in activation energy or rate and hence confirming how the hydrogen is involved in the mechanism.

(Interesting and possibly plausible approach. You could have elaborated a little more, e.g. how to relate the results from this simulation to results from the experiment. Fjs113 (talk) 19:28, 14 May 2018 (BST))

As the momentum of the H-H is varied between 3 and -3 for a reaction between F and H₂, it can be seen that the momenta has an effect on whether the reaction is possible and how much inter-system crossing will occur. At the lowest momentum of -3, the system remains closer to the transition state and the system passes through the transition state many times. As the momenta is increased to a less negative value, the side of the reactants (H₂) is favoured. However, by p_HH=-1.3, the system once again remains close to the transition state and involves lots of crossing, before the product (HF + H) is favoured. AS momenta increases, there is no intersystem crossing and the products instantly form. This pattern repeats once more with p_HH=1.5 favouring reactants, p_HH=2.6 staying near the transition state and p_HH=3 favouring products. All of the systems have a maximum potential energy of approximately -105 kJ/mol. The more momenta in the system, the more intersystem crossing occurs. This is because there is a much larger energy in all of the systems than the activation energy required for hydrogen, so the hydrogen has a large KE as it approaches the F atom and so it will have a larger energy when it is repelled from the Florine, meaning there is more energy for the hydrogens' bond to reform.

p(H-H)	Reactive?	Potential Energy Surface Plot	p(H-H)	Reactive?	Potential Energy Surface Plot
-3.0	No		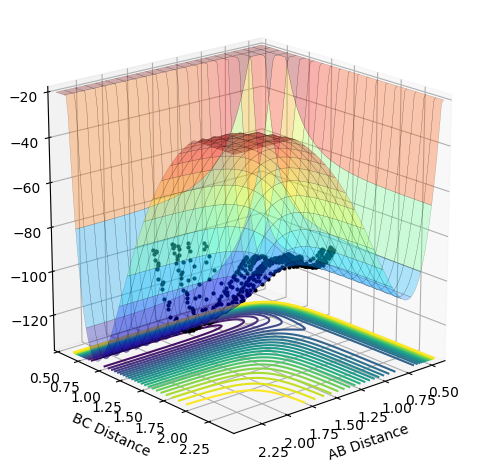-2.8	No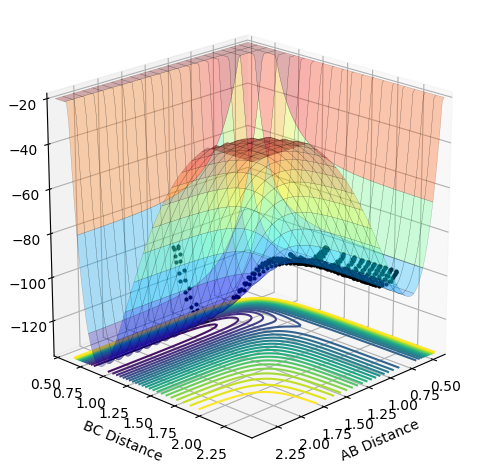
-2.4	No		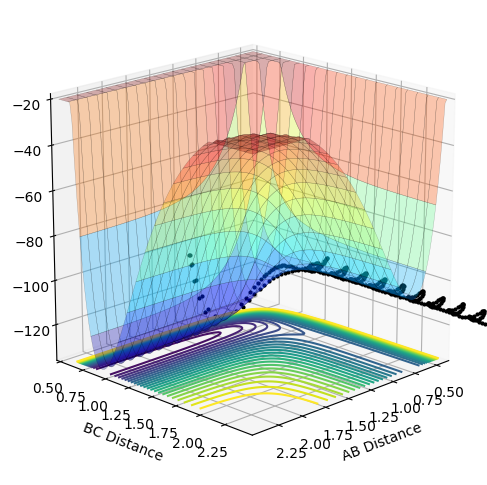-1.3	No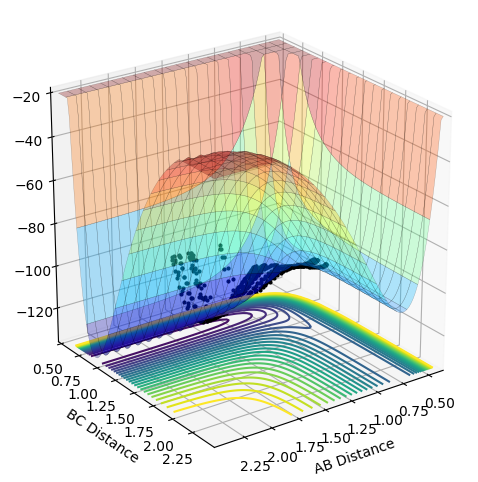
-1	Yes		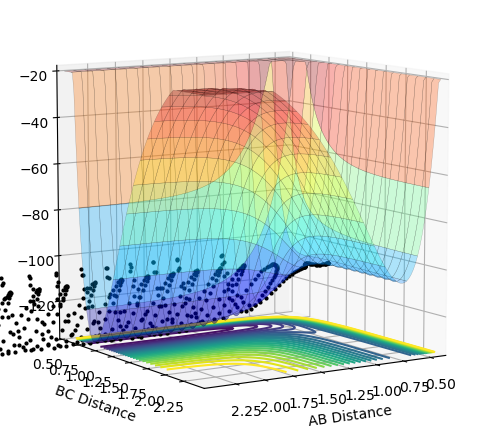1	Yes
1.5	No		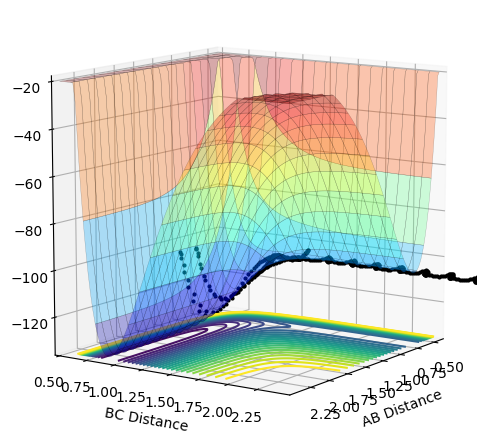2.6	No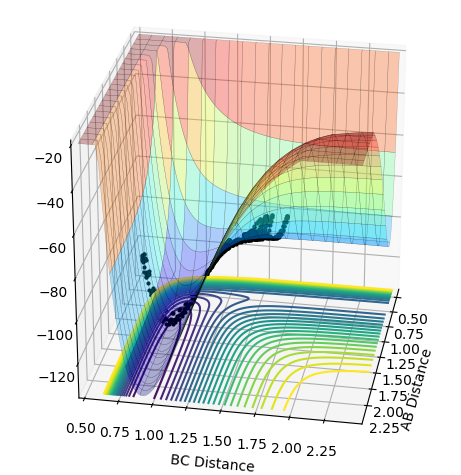
3.0	Yes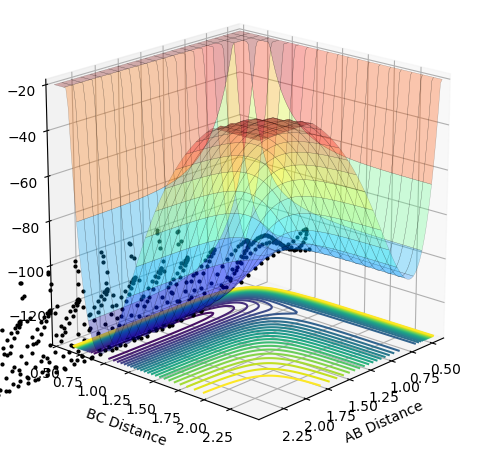

When the overall energy of the system was reduced with p_(HF)=0.8 and p_(HH)=-0.1 then the potential energy surface looked like the figure below and the lower PE H + HF products were formed with no intersystem crossing taking place. There is reduced total energy so it is expected that the molecules will have less potential energy and so there will be less repulsion when the H-F atoms reach the minimum distance of separation. The hydrogen's bond never reforms since the H atoms are never close enough to overcome the stronger H-F attraction and form a new bond.

For the inverse momenta method to find a reaction trajectory, the reaction proceeded to the products with the initial conditions of F-H=0.9, H-H=2.4, p_(FH)=p_-(HH)=5.45. Any conditions where p_-(HH) decreases and p_(FH) increases by the same amount from 5.45 also resulted in a reaction.

Polanyi's Empirical Rules state that vibrational energy is better at promoting a late energetic-barrier to reaction in comparison to translational energy which is more efficient at promoting an early energy barrier to reaction. If the barrier is late, than the transition state at that point will resemble the products more closely than the reactants and vice versa. This means that vibrational energy is better at promoting an endothermic reaction and translational energy is better at promoting an exothermic reaction.

(Would've been nice to see some evidence that this indeed holds, using plots of simulations etc. Fjs113 (talk) 19:28, 14 May 2018 (BST))