MolecularmodellingGMG

Molecular Modelling

Ammonia analysis

Ammonia

Calculation method: RB3LYP

Basis set: 6-31G(d.p)

RMS gradient norm: 0.00000323 au

Point group: C₃V

Final energy: -56.55776873 au

Optimised N-H bond distance: 1.01798

Optimised N-H angle: 105.745°

Item               Value     Threshold  Converged?
 Maximum Force            0.000006     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000014     0.001800     YES
 RMS     Displacement     0.000009     0.001200     YES

The optimisation file is linked here

Vibration frequencies of an ammonia molecule

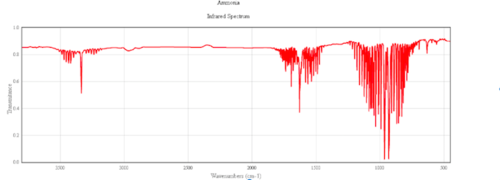
Ammonia is not a linear molecule, so the number of vibrational frequencies is given by 3N-6. N=4 so 6 modes are expected. However, due to degeneracy only 4 modes are actually observed.

- The degenerate vibrations at 3580.82 are due to assymetric stretching.

- The vibration at 3461 is due to stretching and is the most symmetric of all the modes.

- The degenerate vibrations at 1693 are due to bending.

- The vibration at 1089.54 is known as the 'umbrella mode'.

Infra-red spectra of ammonia

Charge on Nitrogen atom: -1.125 Charge on hydrogen atoms: 0.375

It would be expected that Nitrogen to have a negative charge as it a much more electronegative element than Hydrogen.

N₂ analysis

Nitrogen

Calculation method: RB3LYP

Basis set: 6-31G(d.p)

RMS gradient norm: 0.0000060 au

Point group: D_∞H

Final energy: -109.52359111 au

N₂ triple bond distance 1.092 linear molecule

 
  Item                    Value        Threshold  Converged?
 Maximum Force            0.000001     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000000     0.001200     YES
    

The optimisation file is linked here

Vibration frequencies of a N₂ molecule

H₂

Hydrogen

Calculation method: RB3LYP

Basis set: 6-31G(d.p)

RMS gradient norm: 0.00000017 au

Point group: D_∞H

Final energy: -1.17853936 au

H-H bond distance: 0.74279 linear molecule

Item                      Value        Threshold    Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES

The optimisation file is linked here

Vibration frequencies of a hydrogen molecule

Energy of the Haber Process reaction

E(NH₃)= -56.55776873

2*E(NH₃)= -113.1155375

E(N₂)= -109.52359111

E(H₂)= -1.17853936

3*E(H₂)= -3.53561808

ΔE=2*E(NH₃)-[E(N₂)+3*E(H₂)]= -0.05632827 au

ΔE= -147.89 KJ/mol^-1

The reaction is exothermic and the product is lower in energy than the reactants. Therefore NH₃ is more thermodynamically stable than the gaseous reactants.

F₂ analysis

Fluorine

Calculation method: RB3LYP

Basis set: 6-31G(d.p)

RMS gradient norm: 0.00007365 au

Point group: D_∞H

Final energy: -199.49825218 au

F-F bond distance 1.40281

Item                      Value        Threshold    Converged?
 Maximum Force            0.000128     0.000450     YES
 RMS     Force            0.000128     0.000300     YES
 Maximum Displacement     0.000156     0.001800     YES
 RMS     Displacement     0.000221     0.001200     YES

The optimisation file is linked here

Vibration frequencies of a fluorine molecule

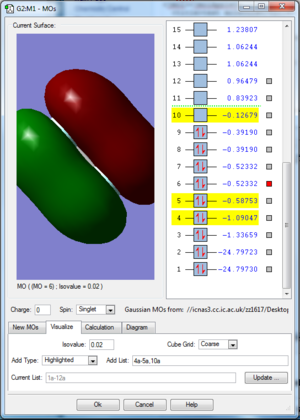
2p orbital combinations

F₂ is a diatomic linear molecule. 2 F atoms form a non-polar cavalent bond. The bond order of F₂ is one. The p orbitals combine to form 2 pi bonds and a sigma bond. Each orbital is labelled with its bonding or anti bonding character, and the number corresponds to which orbital is represented in the diagram from the list of orbital energies. The HOMO and LUMO are not relatively close in energy compared to the other 2p orbitals.

The LUMO of F₂, 3σ_u*, 10

The HOMO of F₂, 2π_g*, 9/8 (2 degenerate orbitals)

1π_u, 7/6 (2 degenerate orbitals)

3σ_g, 5

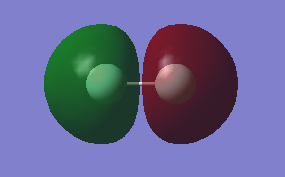
2s orbital combinations

2σ_u*, 4

2σg_g, 3

The orbital energies of F₂

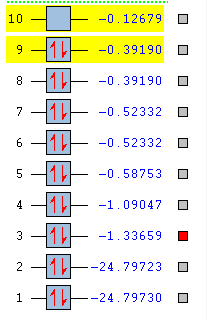
Cyanide analysis

Cyanide

Calculation method: RB3LYP

Basis set: 6-31G(d.p)

RMS gradient norm: 0.00000704 au

Point group: C_∞V

Final energy: -92.82453153 au

Optimised C-N triple bond distance: 1.18409

Item               Value     Threshold  Converged?
 Maximum Force            0.000012     0.000450     YES
 RMS     Force            0.000012     0.000300     YES
 Maximum Displacement     0.000005     0.001800     YES
 RMS     Displacement     0.000008     0.001200     YES

The optimisation file is linked here

Charges on a cyanide molecule

Vibration frequency of an cyanide molecule

Molecular orbitals of cyanide

2s combinations

1σ, 3

2σ*, 4

2p combinations

A triple bond is formed between the C and the N atom. The bond order is 2.5. Due to the difference in electronegativity between C and N (nitrogen is the more electronegative atom) the nitrogen atom has higher bonding character and the carbon higher anti bonding character. The number corresponds to which orbital is represented in the diagram from the list of orbital energies

1π, 5/6 (2 degenerate orbitals)

The HOMO of CN, 4σ, 7

The LUMO of CN, 2π*, 8

The orbital energies of CN