Molecular modelling01368873
NH3
| Calculation Method | Basis Set | Final Energy/au | RMS Gradient/au | Point Group |
|---|---|---|---|---|
| B3LYP | 6-31G (D,P) | (-56.55776873) | 0.00000485 | C3 |
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
The bond length between N and H is 1.01798 angstroms The bond angle for H - N - H is 105.741 degrees
test molecule |
The link to my NH3 file is here
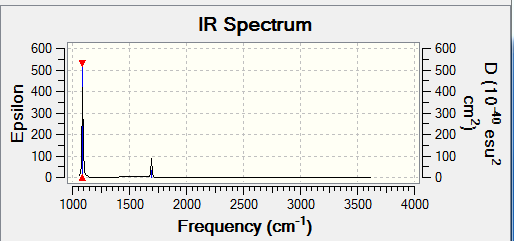
The display vibrations for NH3

The expected number of vibrational modes should be 6 but due to degeneracy there are actually only 4 vibrational modes. Of these vibrational modes the bending modes are at 1089.54 s -1 and 1693.95 s -1 , whilst the bond stretching modes are at 3461.29 s s-1 and 3589.82 s -1 . The highly symmetric mode 3461.29 s-1 is at and the umbrella mode is at 1089.54 s -1. The number of bands expected in an experimental spectrum of gaseous ammonia is 1 as the bonds are all the same and is from the umbrella mode, however there are 2 bands in the spectrum as shown below. The main reason for the 2 peaks on the IR is because these vibrations cause a significant change in the dipole. Another reason for two peaks is because the vibrations at 2 frequencies(1089.54s-1 and 1693.95s-1)have intensities (145.3814, 13.5533) that are high enough to be seen on the spectrum.
The charges expected for nitrogen was -1 and for hydrogen was +0.5 because nitrogen is more electronegative so would withdraw more electron density towards its nucleus. The values found on Gaussian was -1.125 for nitrogen and +0.375 for hydrogen.
N2
| Calculation Method | Basis Set | Final Energy/au | RMS Gradient/au | Point Group |
|---|---|---|---|---|
| B3LYP | 6-31G (D,P) | (-109.52412868) | 0.00000365 | D∞h |
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000002 0.001800 YES RMS Displacement 0.000003 0.001200 YES
The bond length between N and N is 1.10550 angstroms
test molecule |
The link to my N2 file is here A nitrogen molecule has one vibrational mode at a frequency of 2457.31 s-1
H2
| Calculation Method | Basis Set | Final Energy/au | RMS Gradient/au | Point Group |
|---|---|---|---|---|
| B3LYP | 6-31G (D,P) | (-1.17853930) | 0.00012170 | D∞h |
Item Value Threshold Converged? Maximum Force 0.000211 0.000450 YES RMS Force 0.000211 0.000300 YES Maximum Displacement 0.000278 0.001800 YES RMS Displacement 0.000393 0.001200 YES
The bond length between H and H is 0.74309 angstroms
test molecule |
The link to my H2 file is here A hydrogen molecule has one vibrational mode at a frequency of 4461.48 s-1
Reaction Energy
- E(NH3)= -56.55776873 au - 2*E(NH3)= -113.11553746 au - E(N2)= -109.52412868 au - E(H2)= -1.17853930 au - 3*E(H2)= -3.5356179 au - ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579096 au
The energy required to form ammonia gas from nitrogen gas and hydrogen gas in the Haber-Bosch reaction is -146.48 KJmol-1. Literature value for the energy required is -46.19 kJmol-1[1]. The reason for the difference in energy is because the value calculated is based off of theory whilst the other is experimental.
Nitrogen gas and hydrogen gas are not as stable as ammonia gas and so as it has the most exothermic energy and so is the most stable. Nitrogen gas, however, is around 10 times more stable than hydrogen gas, so is closer in stability to ammonia than hydrogen gas.
PH5
| Calculation Method | Basis Set | Final Energy/au | RMS Gradient/au | Point Group |
|---|---|---|---|---|
| B3LYP | 6-31G (D,P) | (-344.25491049) | 0.00000456 | C3 |
Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000046 0.001800 YES RMS Displacement 0.000019 0.001200 YES
The bond lengths between P and H are 1.48691 angstroms (2 H in the same plane) and 1.43320 angstroms (3 H in the same plane) The bond angle between the 2 H atoms in the same plane is 180 degrees, the bond angle between the 3 H atoms in the same plane is 120 degrees and the bond angle between the H atoms in different planes is 89.999 degrees.
test molecule |
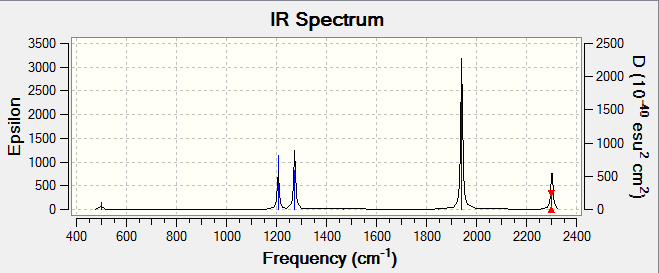
The link to my PH5 file is here
PH5 has 12 vibrational modes but due to degeneracy there are actually 8 vibrational modes at the following frequencies; 498.01s-1(bending mode), 1206.92s-1(bending mode), 1272.94s-1(bending mode), 1469.97s-1(bending mode), 1847.92s-1(stretching mode), 1940.95s-1(stretching mode), 2296.29s-1(stretching mode), and 2301.98s-1(stretching mode). On the infrared spectrum, only 5 peaks can be seen because these vibrations cause a significant change in the dipole that is detected by infra red, also the intensities are high and significant enough to be visible on the infrared spectrum.
The charge distribution for PH5 is as follows, phosphorous has a charge of +0.412, the 3 hydrogen atoms planar to each other have a charge of -0.015 and the 2 hydrogen atoms linear to each other have a a charge of -0.183. Phosphorous is a much larger atom than hydrogen so even though the nuclear charge is much higher, the surrounding electrons shield this charge, making phosphorous less electronegative than hydrogen hence the result in the charge distribution of PH5. Overall, however, the molecule is neutral.
Hydrogen has an electron configuration of 1s1. Phosphorous has an electron configuration of 1s2 2s2 2p6 3s2 3p3. The electrons involved in bonding are the electrons in the 3s and 3p orbitals of phosphorous and the electron found in each 1s orbital of the hydrogen atoms.
Molecular Orbital 1- This molecular orbital is an occupied sigma gerada bonding orbital made up of the 3s atomic orbital of phosphorous and a 1s atomic orbital from hydrogen. it has an energy of -0.68487au.
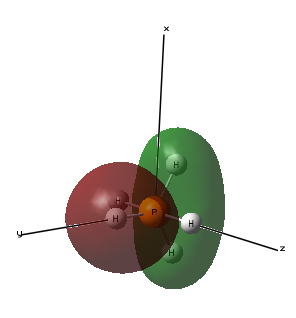
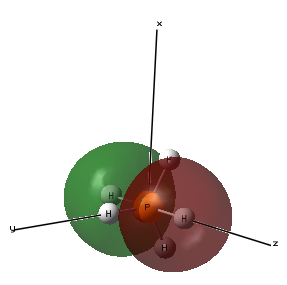
Molecular Orbital 2- This molecular orbital is an occupied sigma ungerada bonding orbital made up of the 3px atomic orbital of phosphorous and the atomic 1s orbitals of the 2 hydrogen atoms in the same plane as they are in the same phase as the 3px orbital phases.
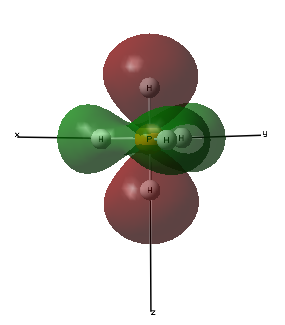
Molecular Orbital 3- This molecular orbital is an occupied sigma gerada bonding orbital made up of the 3py atomic orbital of phosphorous and 1s atomic orbitals of the 3 hydrogen atoms in the same plane as the phases are the same as the 3py orbital. This molecular orbital happens to be degenerate in energy with molecular orbital 2, they both have the energy -0.42681au.
Molecular Orbital 4- This molecular orbital is an occupied sigma gerada bonding orbital made up of the 3pz atomic orbital of phosphorous and a 1s atomic orbitals of the 2 hydrogen atoms in the same plane as they are in the same phase as the 3pz orbital. This molecular orbital has the energy -0.40947au which is similar in energy with molecular orbital 2 as they both involve 2 hydrogen atoms.
Molecular Orbital 5- This molecular orbital is one that is too deep in energy to be used in bonding as it depicts the 2p orbitals of the phosphorous atom. It is degenerate in energy as there are 3 full 2p orbitals that are all equal in energy and so all have the same orbital structure along each of the Cartesian axes (x,y,z). They have very similar if not degenerate energies of -4.77au to 2 decimal places.
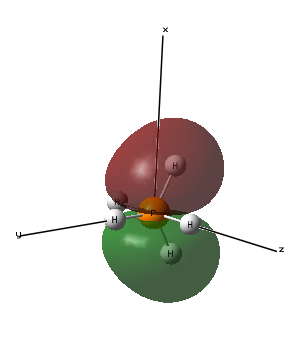
Molecular Orbital 6- This molecular orbital is the highest occupying molecular orbital and uses a 3d atomic orbital from the phosphorous and 1s atomic orbitals from the hydrogen atoms, the 3 hydrogen atoms in the same plane mix with one phase of the phosphorous orbital and the 2 hydrogen atoms in the same plane mix with the other phase of the phosphorous orbital to form the molecular orbital that involves all the atoms in the molecule. This looks like a dz2 orbital but it has been distorted with the bonding with the 1 s orbitals. As it is the highest occupying molecular orbital, its energy is closest to 0 and has energy -0.21463au.
References
- ↑ Bhattacharjee, S., "TEST: The Expert System for Thermodynamics," Electronic Resource, Entropysoft, Del Mar, CA, http://www.thermofluids.net. Last accessed on: 16/03/2018