Molecular Reaction Dynamics (st4215)

In this computational lab, the reactivity of triatomic systems - where a single atom and a diatomic molecule collide - is studied. This is done by calculating Molecular Dynamics trajectories using a MATLAB software.

Exercise 1: H + H₂ system

The first exercise involves a triatomic system with the atom H₃ colliding with the diatomic molecule H₁-H₂. The initial input values used to calculate the trajectories of the atoms are shown below:

	Initial distance between atoms	Initial momentum
H1 and H2	r1(0) = rBC(0) = 0.74	p1(0) = pBC(0) = 0
H2 and H3	r2(0) = rAB(0) = 2.30	p2(0) = pAB(0) = -2.7

The transition state

Any molecular trajectory proceeds via a transition state, which is defined as the maximum on the minimum potential energy path linking reactants and the products. Hence in determining whether a molecular trajectory is reactive, the position of the transition state is first determined - a reactive trajectory will pass through the transition state and move towards the formation of the products.

The maximum on the minimum energy path shown in this PES corresponds to the transition state.

Dynamics of the transition state

A potential energy surface is generated from a trajectory calculation. We can identify the approximate position of the transition state by locating the maximum on this surface.

What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.

At both a minimum and at a transition structure in the potential energy surface, the total gradient is 0. However, as the transition state corresponds to a maximum on the potential energy surface, it can be distinguished from the various minima by the second derivative. At a maximum where the transition state is located, the second derivative will be negative, while at the minima, the second derivative will be positive.

Locating the transition state

The transition state can be located by setting r₁ = r₂ , since the H + H₂ surface is symmetric, and p₁ = p₂ = 0.0. The latter condition is because by starting a trajectory on the ridge, with no gradient in the direction at right angles to the ridge, the trajectory will remain oscillating on the ridge and never fall off, enabling us to locate the TS geometry.

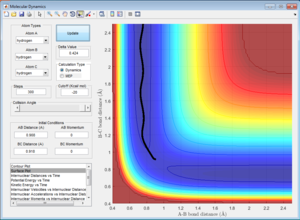
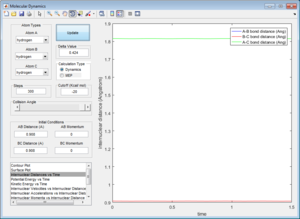
Report your best estimate of the transition state position (r_ts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.

The transition state position is achieved when the r₁ = r₂ = r_ts = 0.908. This is evident from the graph below where it can be seen that internuclear distance does not vary with time when r_ts = 0.908. This means that the transition state has been achieved as distance between atoms are no longer changing.

Internuclear distances remain constant over time when r_ts = 0.908.

Trajectories from the transition state

If a trajectory is started at the transition state but is not given an initial momentum, it will not move. However, by displacing the positions slightly from the transition state with zero initial momenta, the reactants may "roll" towards the products and we can find the resulting trajectory.

To do this, the following initial conditions were set:

	Initial distance between atoms	Initial momentum
H1 and H2	r1 = rBC = rts+0.01 = 0.918	p1 = pBC = 0
H2 and H3	r2 = rAB = rts = 0.908	p2 = pAB = 0

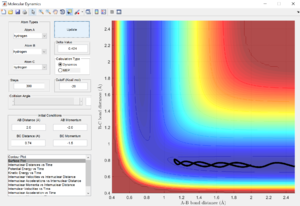
Calculating the reaction path

The reaction path (or minimum energy path, mep) is a special trajectory that corresponds to infinitely slow motion (i.e. the velocity always reset to zero in each time step).

Comment on how the mep and the trajectory you just calculated differ.
Calculation via the minimum energy path shows a trajectory which follows the valley floor directly in a straight line to H₁ + H₂-H₃. However, the trajectory generated from a dynamics calculation is a wavy line instead, as the diatomic molecule is vibrating. This is because the mep calculation type calculates the minimum vibrational energy state of the molecule at each point in the reaction, and hence shows a straight line, whereas the dynamics calculation takes into account vibrations and oscillations between different vibrational energy levels, hence the line is wavy.

• 

  The trajectory generated from an mep calculation shows a straight line.

• 

  The trajectory generated from an dynamics calculation shows a wavy line.

(Fv611 (talk) 16:02, 24 May 2017 (BST) Yes, but why is the mep straight and the dynamic-generated line wavy? Hint: it has to do with how both methods treat velocity.) Using the graph of internuclear distance against time as well as internuclear momenta against time, we can determine the final values of positions r₁(t) and r₂(t) as well as the average momenta p₁(t) and p₂(t) at large values of t.

• 

  Graph of internuclear distance against time

• 

  Graph of internuclear momenta against time

• Final distance between atoms		Final momentum
  x value	y value	x value	y value
  t = 1.495	r1(t) = rBC(t) = 5.281	t = 1.495	p1(t) = pBC(t) = 2.481
  t = 1.495	r2(t) = rAB(t) = 0.7453	t = 1.495	p2(t) = pAB(t) = 1.555

Reactive and unreactive trajectories 

From the previous calculations, it can be concluded that trajectories with initial conditions in the range r₁ = 0.74, r₂ = 2.0, with -1.5 < p₁ < -0.8 and p₂ = -2.5 are reactive. Although it seems reasonable to assume that all trajectories starting with the same positions but higher values of momenta would be reactive, since they have enough kinetic energy to overcome the activation barrier, this is not necessarily true. This can be illustrated in the following examples.

Using the initial atom positions r₁ = 0.74 and r₂ = 2.0, trajectories were run with the following momenta combinations:

	p1	p2	Result
Trajectory 1	-1.25	-2.5	Reactive
Trajectory 2	-1.5	-2.0	Unreactive
Trajectory 3	-1.5	-2.5	Reactive
Trajectory 4	-2.5	-5.0	Unreactive
Trajectory 5	-2.5	-5.2	Reactive

Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.

	Screenshot	Description
Trajectory 1		In this trajectory, it can be seen that B-C bond distance (r1) remains relatively constant as A-B bond distance (r2) decreases, indicating that H1 is moving closer to H2-H3. When r1 = r2 = 0.9012 at t = 0.43, the transition state is reached. The molecules then move into the product channel where r1 increases as H3 moves further away from H1-H2. Hence this trajectory is reactive.
Trajectory 2		This trajectory is clearly unreactive. Initially, r1 remains relatively constant as r2 decreases, indicating that H1 is moving closer to H2-H3. However, the trajectory then shows that r2 starts to increase again - meaning that H1 starts to move away again. Hence the product H1-H2 is clearly not formed.
Trajectory 3		Similar to Trajectory 1, this trajectory is reactive as the potential energy surface plot clearly shows the molecules moving into the product channel. Initially r2 decreases with r1 remaining relatively constant, indicating that H1 is moving closer to H2-H3. Eventually the transition state is reached and r1 increases as H3 moves further away from H1-H2.
Trajectory 4		This trajectory is also unreactive. Like in Trajectory 2, r1 remains constant as r2 decreases, indicating that H1 is moving closer to H2-H3. However, although r2 then starts to decrease, this does not mean that H1-H2 has formed as the trajectory shows the molecules "bouncing back" to the reactant channel with H1 moving further away from H2-H3 again.
Trajectory 5		This trajectory is reactive. Although the molecules bounce back to the reactant channel, it can be seen that they cross the barrier again towards the product channel with a small value r2 and increasing r1, indicating that H1-H2 has formed and H3 is moving further away.

Transition state theory

From the examples above, we can see that trajectories starting from the correct initial positions but with higher values of momenta are not necessarily reactive. However, such cases of unreactivity are not accounted for by the transition state theory. The transition state theory (TST) enables us to quantify the rate of a reaction if the estimated properties of the transition state are known. However, it is based on several limitations, and hence reaction rates determined theoretically by TST may deviate from experimentally determined values.

State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

One of the limitations of the TST is that it assumes that atomic nuclei behave according to classical mechanics. Hence it makes the assumption that as long as atomic nuclei collide with sufficient energy to form the transition structure, the reaction will proceed and the products will be formed. This means that atomic nuclei colliding with insufficient energy do not react, and those colliding with more than enough energy are able to react. However, from the examples discussed above, we know that this is not true, as unreactive trajectories can also result even with higher values of momenta (and hence kinetic energy). In general, rates calculated using the TST are lower than experimentally determined values, as it does not account for reactive trajectories whereby atomic nuclei do not have enough energy to overcome the activation barrier. Such nuclei may still be able to react via quantum tunnelling through the barrier. This is especially predominant in reactions with low activation energy barriers.

Another assumption that the TST makes is that the reaction system will always pass over the lowest energy saddle point on the potential energy surface, which corresponds to the transition state. However, this is not necessarily the case. Especially at higher temperatures, molecules may populate higher energy vibrational levels. Collisions may therefore lead to transition states which are not necessarily at the lowest energy saddle point. Hence as the TST does not account for these possibilities, the calculated rate will be lower than experimentally determined values.

(Fv611 (talk) 16:02, 24 May 2017 (BST) Good discussion, but how does TST describe recrossing?)

Exercise 2: F - H - H system

In this exercise, the F-H-H triatomic system is studied whereby the atom F collides with the diatomic molecule H₁-H₂.

Inspection of the potential energy surface

Reaction energetics

Classify the F + H₂ and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
The F + H₂ → H + HF reaction is exothermic, while the reverse reaction (H + HF → F + H₂) is endothermic. This indicates that the H-F bond strength is greater than the H-H bond strength.

Locating the transition state

Locate the approximate position of the transition state.
The transition state was determined by a similar method as in Exercise 1. The initial conditions below gave the position of the transition state:

	Initial distance between atoms	Initial momentum
F and H1	rAB = rFH = 1.81	pAB = pFH = 0
H1 and H2	rBC = rHH = 0.74	pBC = pHH = 0

As explained above, setting the initial momenta as 0 for both enables us to locate the position of the transition state by constraining it to a point on the ridge. r_BC = r_HH was set at 0.74 as this is the H-H bond distance in H₂. Varying r_AB = r_FH by trial and error allowed us to determine its value at 1.81. This was guided by Hammond's Postulate, which states that in an exothermic reaction like this one, the transition state will be closer to the reactants. Hence r_AB = r_FH should be higher than r_BC = r_HH.

This can be confirmed by the potential energy surface plot (using an mep calculation) as well as the graph of internuclear distance against time. Both show that when r_AB = r_FH = 1.81, the molecule is not moving, oscillating or vibrating, indicating that it has attained the transition state position.

• 

  Potential energy surface (using mep calculation)

• 

  Graph of internuclear distance against time

Activation energy

Once the position of the transition state has been determined, the activation energies for the forward and reverse reactions can be calculating by slightly displacing the atoms from the transition state position - the saddle point on the potential energy surface. Depending on where the initial position is relative to the transition state, the atoms will naturally roll down (without any initial momentum) towards either the reactants (F + H₂) or the products (H + HF). Displacing the atoms from the transition state position is necessary as starting the trajectory at the transition state (with no initial momentum) would mean that the atoms will remain there forever.

Report the activation energy for both reactions.
It was previously determined that the transition state was attained when r_AB = r_FH = 1.81 and r_BC = r_HH = 0.74. Hence the following conditions were used to determine the respective activation energies:

	rAB = rFH	rBC = rHH
F + H2 → H + HF (forward reaction)	1.82	0.74
H + HF → F + H2 (reverse reaction)	1.80	0.74

with no initial momentum being given (p_FH = p_HH = 0) for both cases.

Activation energies can then be determined by looking at the drop in potential energy as the reactants move towards the products.

• 

  Change in potential energy against time for the forward reaction.

• 

  Change in potential energy against time for the reverse reaction.

	Initial (reactants)	Final (products)	Activation energy / kcal mol-1
F + H2 → H + HF (forward reaction)	x = 0.085 y = -103.8	x = 400 y = -103.9	-103.8 - (-103.9) = 0.1
H + HF → F + H2 (reverse reaction)	x = 73.66 y = -103.8	x = 98.46 y = -133.6	-103.8 - (-133.6) = 29.8

It can be seen that potential energy for the forward reaction does not taper off to a constant value despite the large number of steps used in the calculation; this is likely due to the very small activation energy for the reaction and hence the value calculated may be limited in accuracy.

(Fv611 (talk) 16:02, 24 May 2017 (BST) Good, well done on pointing out that the mep doesn't converge.)

Reaction dynamics

Reaction energy

Identify a set of initial conditions that results in a reactive trajectory for the F + H₂, and look at the “Animation” and “Internuclear Momenta vs Time”. In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

By trial and error, the initial conditions below were determined to give a reactive trajectory for F + H₂ → H + HF:

	Initial distance between atoms	Initial momentum
F and H1	rAB = rFH = 2.30	pAB = pFH = -2.7
H1 and H2	rBC = rHH = 0.74	pBC = pHH = 0

The resulting potential energy surface plot confirms that the forward reaction F + H₂ → H + HF is exothermic as the products are lower in energy that the reactants.

F + H₂ → H + HF is an exothermic reaction

We can confirm this experimentally by calorimetry - knowing the energy difference between reactants and products allows us to calculate the amount of heat released and hence the corresponding increase in temperature. Measuring this increase in temperature allows us to confirm that that this exothermic reaction has indeed occurred.

• 

  Potential energy surface for this trajectory

• 

  Graph of internuclear momenta against time

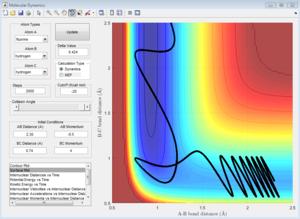
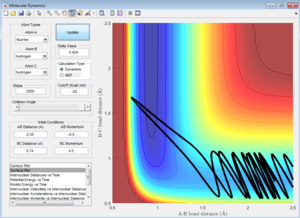
From the potential energy surface plot, we can also see that most of the energy input into the system is converted into vibrational energy. This is evident as the atoms do not move in a straight translational motion but in a wavy motion. As A-B (F-H₁) bond distance decreases, corresponding to conversion to translational energy, it can be seen that B-C (H₁-H₂) bond distance is oscillating, indicating that energy is also converted to vibrational energy. Similarly, after the activation barrier is crossed, A-B (F-H₁) bond distance oscillates greatly as B-C (H₁-H₂) bond distance increases, indicating that most of the energy input is converted to vibrational energy (oscillation) rather than translational energy (decreasing of B-C bond distance).

We can confirm this experimentally by IR spectroscopy. As can be seen in the graph of internuclear momenta against time, the frequency and amplitude of vibrations change over time as reactants move to products. Comparing the IR spectrum of the reactants and products firstly allows us to confirm that the energy is vibrational in nature - large peaks should be seen on the IR spectrum. Differences in frequency of vibration also allows us to distinguish between products and reactants and that the reaction has indeed taken place.

Investigating Polanyi's empirical rules

Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

Polanyi's rules state that vibrational energy is more efficient in promoting a reaction with late transition states, while translational energy is more efficient in promoting reactions with early transition states. This can be illustrated in the trajectories discussed below.

Calculation 1: F + H₂ → H + HF
A calculation with the following initial conditions was set up, varying the value of p_HH in the range -3 to 3 to investigate the effect on the resulting trajectories.

	Initial distance between atoms	Initial momentum
F and H1	rAB = rFH = 2.30	pAB = pFH = -0.5
H1 and H2	rBC = rHH = 0.74	-3 ≤ pBC = pHH ≤ 3

It was found that all trajectories with these values of p_HH were unreactive due to various reasons.

Magnitude of pHH	Screenshot	Description
|pHH| = 0	pHH = 0	When pHH = 0, meaning that no initial momentum is given to H-H, the atoms do not have enough energy to cross the activation barrier, and their motion stops abruptly before even reaching near the transition state position.
|pHH| = 1	pHH = -1 pHH = 1	Increasing the magnitude of pHH to 1 increases the amount of vibrational energy given to the reactants. However, in both cases, it can be seen that the atoms still do not have enough energy to cross the activation barrier.
|pHH| = 2	pHH = -2 pHH = 2	When pHH = -2, atoms do not have enough energy to cross the activation barrier and return to the reactants. When pHH = 2, the atoms have enough energy to cross the activation barrier, however they bounce back, resulting in an unreactive trajectory.
|pHH| = 3	pHH = -3 pHH = 3	Increasing the magnitude of pHH to 3, meaning an increase in the vibrational energy given to the reactants, give the atoms enough energy to cross the activation barrier. However, the trajectory is still unreactive as the atoms bounce back after crossing the barrier.

This is an expected result, as the forward reaction F + H₂ → H + HF is exothermic and therefore has an early transition state. Based on Polanyi's rules, translational energy plays a more important factor than vibrational energy in promoting the reaction. However, in the above cases, the molecule was given varying amounts of vibrational energy (p_HH) which were often much greater than translational energy (p_FH = -0.5). Hence, it is expected that these initial conditions would result in unreactive trajectories.

Increasing the magnitude of p_HH to 4, however, gives an unexpected result - reactive trajectories are obtained. This is perhaps due to the very large amount of vibrational energy given to the molecules. However, this is likely an exception, as increasing the magnitude of p_HH to 4.5 again gives unreactive trajectories with the atoms bouncing back after crossing the activation barrier.

• 

  p_HH = -4

• 

  p_HH = 4

• 

  p_HH = -4.5

• 

  p_HH = 4.5

Following Polyani's rules and giving the atoms more translational energy by increasing the momentum p_FH = -0.8, and considerably reducing the momentum p_HH = 0.1, gives reactive trajectories as expected. Further increasing p_FH to -1 and -2 also result in similarly expected reactive trajectories.

• 

  p_FH = -0.8

• 

  p_FH = -1

• 

  p_FH = -1

Calculation 2: H + HF → F + H₂
Polanyi's rules are also exemplified in the reverse reaction, H + HF → F + H₂. This reaction is endothermic and therefore has a late transition state. Hence, according to Polanyi's rules, vibrational energy should be more efficient in promoting this reaction.

Indeed, low values of vibrational energy (p_FH) and high values of translational energy (p_HH) give unreactive trajectories:

• 

  p_FH = 0.1, p_HH = -6

• 

  p_FH = 1, p_HH = -7

• 

  p_FH = 0.5, p_HH = 4

However, increasing vibrational energy (p_FH) and reducing translational energy (p_HH) allow us to obtain reactive trajectories:

• 

  p_FH = 6, p_HH = -1.7

• 

  p_FH = 6.9, p_HH = -1

• 

  p_FH = 7.7, p_HH = 0.4

Hence both calculations show that Polanyi's rules provide a good basis to determine whether the distribution of energies (between translational or vibrational modes) are efficient in promoting a certain reaction depending on whether it has a early or late transition state.

(Fv611 (talk) 16:02, 24 May 2017 (BST)Very good discussion + examples)