Molecular Reaction Dynamics:Elizabeth Morgan

Modelling the H + H₂ System

Figure 1: A potential energy surface diagram for the reaction between H₂ and H, rotated to show the saddle point.

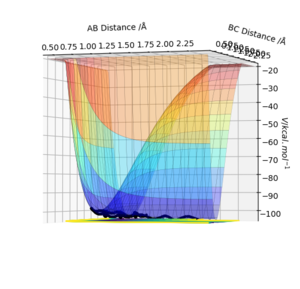
Defining the transition state

On a potential energy surface diagram, the transition state of a reaction is mathematically defined as the point where ∂V(r_i)/∂r_i=0. Taking the derivative of the tangent (q₁) to the inflection point of the reaction pathway, the value of ∂V(q₁)/∂q₁=0. In addition, taking the derivative of the line perpendicular to that tangent (q₂) would also give a result of 0.

Furthermore, ∂²V(q₁)/∂q₁² will give a maximum, while ∂²V(q₂)/∂q₂² will give a minimum.

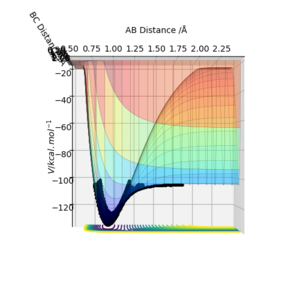
The transition state can be distinguished from other minima on a surface plot since it is is the saddle point; if the trajectory was started at the transition state with no momentum, it would remain there indefinitely. If the geometry was then changed slightly, the trajectory would "roll" towards either the reactants or products. As displayed in Figure 1, the transition state can be identified as the maximum position along the minimum energy path.

Figure 2: A plot of the changes in r with respect to time.

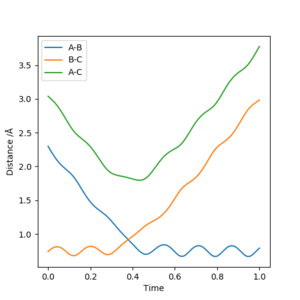
Finding r_ts

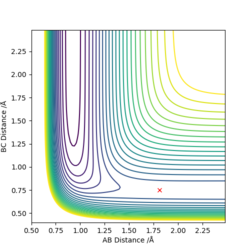
The value of r_ts is 0.92 Å to 2 d.p., and can be found using Fig. 2. r_ts is the instance where r_AB=r_BC, and therefore the intersection of the two plots for r_AB and r_BC will give the value. It occurs at 0.38 time units.

MEPs and reaction trajectories

Figure 3: An MEP plot of the reaction trajectory between H and H₂.

MEPs (minimum energy pathways) differ from dynamic trajectories because the MEPs offer a perspective of the trajectory of the particle at an infinitely slow rate. This means that at each time interval, the program disregards any previous momentum possessed by the particle, and so it starts again at 0. Therefore, if the trajectory passes over an area where the gradient of the surface plot is equal to 0, it will stop.

In contrast, dynamic calculation types take into account and carry over any previous momentum possessed by the particle, and therefore displays the oscillations of the atoms around the bond, and will also allow the trajectory to continue over an area of the plot with 0 gradient.

This is a good explanation, clearly demonstrating your understanding of the differing calculation methods here and how they manifest in the appearance/trajectory of the reaction coordinate.Rk2918 (talk) 21:44, 15 May 2019 (BST)

Reactive and unreactive trajectories

p1	p2	Etot	Reactive?	Description of the dynamics
-1.25	-2.5	-99.182	Yes	This is a simple reaction where the reactants come together with sufficient energy to overcome Ea and therefore form the products. The transition state is only formed once.
-1.5	-2.0	-100.619	No	The reactants travel towards each other, before moving apart again. The reaction does not occur because the reactants do not possess sufficient energy to overcome Ea and form the transition state.
-1.5	-2.5	-99.119	Yes	The reactants travel towards each other with sufficient energy to overcome Ea, and therefore form the products. The transition state is only formed once.
-2.5	-5.0	-85.119	Yes	The transition state is formed 3 times here, since the reactants possess sufficient energy to overcome Ea three times. This means that at the end of the reaction coordinate, the products have been formed with atom A and B bonded, and C dissociated.
-2.5	-5.2	-83.579	No	The reactants possess enough energy to overcome Ea twice, and so the transition state is formed 2 times. This means that the reaction does not go through to the products since the reactants are reformed via the second transition state.

From the table we can conclude that energy is not necessarily the deciding factor in whether a reaction follows through to completion.

Good observations but to be completely clear here it would be more accurate to say that it is not the whole total energy that is the deciding factor. Because the energy is the deciding factor but not necessarily just the magnitude of it.Rk2918 (talk) 21:49, 15 May 2019 (BST)

Transition State Theory

The main assumptions of Transition State Theory are:

- That the rate of reaction can be determined by studying the saddle point of an energy-reaction coordinate diagram. The saddle point corresponds to the transition state.

- The activated complexes near the saddle point of the reaction potential energy surface are in 'quasi-equilibrium' with the reactants.

- The products are formed from these activated complexes, and the rate of this conversion can be found using kinetics.

What about barrier recrossing? In real life reactions, can systems cross back over the barrier? In TST, can systems cross back over the barrier? How would this manifest in the prediction of the reaction rate?Rk2918 (talk) 21:53, 15 May 2019 (BST)

Modelling the F-H-H System

Potential energy surface inspection

Figure 5: An MEP plot of the reaction between H + HF, displaying the approximate position of the transition state.

Figure 4: A potential surface plot of the reaction between H + HF.

Figure 6: A potential surface plot of the reaction between F + H₂.

Figure 7: An MEP plot of the reaction between F + H₂, displaying the approximate position of the transition state.

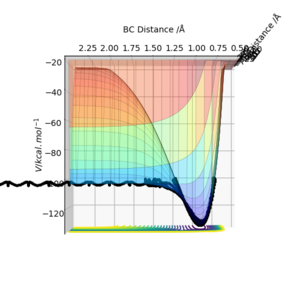
The reaction of H + HF is endothermic, as displayed by Figure 4. The reaction PE increases as the products move away from each other after passing through the transition state, and therefore energy must be absorbed. In relation to bond strength of products vs reactants, since the reaction is endothermic the bond strength of the reactants is stronger than that of the products since more energy is required to break the H-F bond than is released in the formation of the H-H bond. The approximate position of the transition state is:

r_FH = 0.75 to 2 dp

r_HH = 1.81 to 2 dp

The activation energy for the reaction is 142 kJ/mol

The reaction of H₂ + F is exothermic, again as displayed by Figure 6. The potential energy surfaces show that the PE decreases as the reactants pass through the transition state and form the products, which suggests that energy is released. It also follows that the bond strength of the products is greater than that of the products. The approximate position of the transition state is:

r_FH = 1.81 to 2 dp

r_HH = 0.75 to 2 dp

The activation energy for this interaction can be found to be 1.68 kJ/mol

I don't think you're being clear here about how you are determining the activation energies.Rk2918 (talk) 22:57, 15 May 2019 (BST)

Reaction dynamics

Initial conditions that result in a successful reaction between H₂ and F:

r_HH = 0.75

r_HF = 1.81

p_HH = 0

p_HF = -1

From the momentum-time plot, it can be seen that total momentum is conserved, and therefore there is no change to the kinetic energy of the particles. Since there is a decrease in the potential energy of the system due to the fact that it is an exothermic reaction, the energy must be released into the surroundings. This could be confirmed through the use of a calorimeter.

For future reference, if you are discussing a plot, it is best to include it otherwise it is slightly confusing for the reader.Rk2918 (talk) 22:59, 15 May 2019 (BST)

The Polanyi Rules state that a vibrational mode of energy is more efficient for overcoming the activation barrier of a reaction than translational energy.

This is not a complete definition of Polanyi's rules however you have demonstrated in the following that you do have a complete understanding of the rules. Just make sure you are thorough and clear in your explanations.Rk2918 (talk) 22:59, 15 May 2019 (BST)

For the reaction of H + HF, the transition state resembles the products due to the fact it is endothermic (Hammonds Postulate). Having a greater proportion of the energy as a vibrational mode within the H-F bond results in a more efficient reaction. This is consistent with Polanyi's Rules.

The reaction H₂ + F is exothermic, and therefore the transition state will resemble the reactants. However, the reaction is most efficient when the majority of the energy is within the translational mode between H and F.