Molecular Modelling
NH3 Molecule
The molecule is NH3 (ammonia)
Calculation method: RB3LYP
Basis set: 6-31G(d.p)
Final energy: -56.55776873 a.u.
RMS gradient: 0.00000485
Point group: C3V
N-H Bond distance: 1.01798
H-N-H Bond angle: 105.741
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
test molecule |
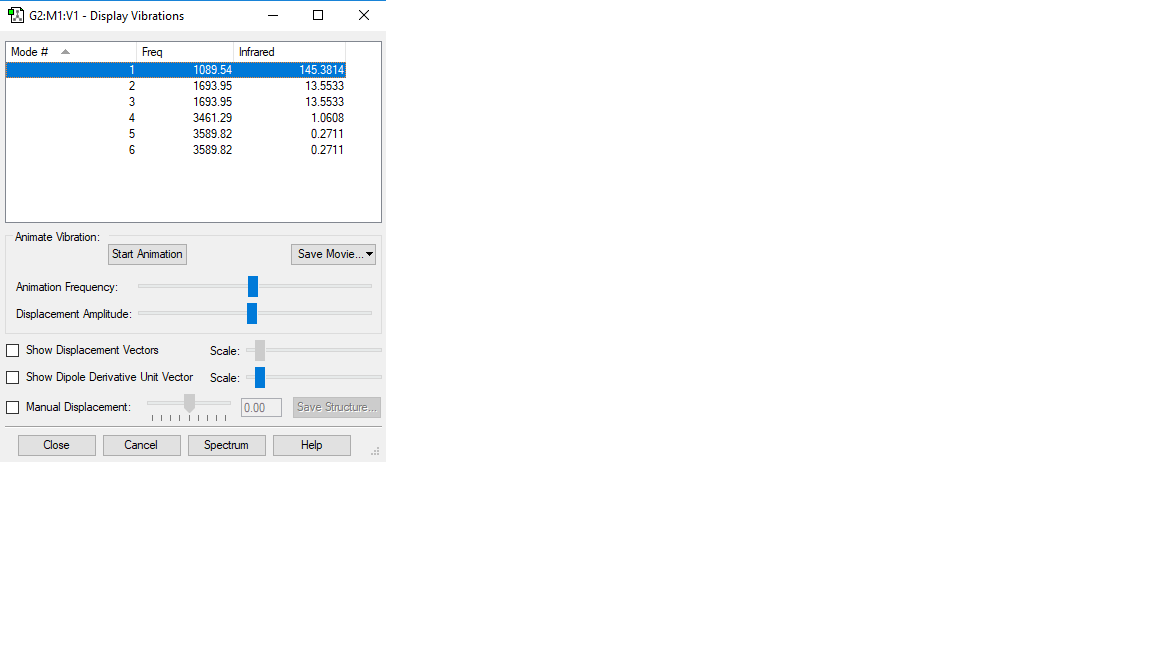
We would expect 6 modes from the 3N-6 rule The second and third modes are degenerate, as are the fifth and sixth modes. The bending modes are the first, second and third, while the fourth, fifth and sixth are stretching modes. The fourth mode is highly symmetric. The 'umbrella mode' could be used to describe the first mode. The spectrum of gaseous ammonia would give us three bands, because only three of the modes give a change in dipole. The atomic charges: N:-1.125 H:0.375 We would expect the N to be negative and the hydrogen atoms to be positive because the nitrogen atom is more electronegative, therefore has a higher tendency to pull electron density towards itself.
Optimization file: here
N2 Molecule
This molecule is nitrogen.
Calculation method: RB3LYP
Basis set: 6-31G(D,P)
Total energy: -109.52412868 a.u.
RMS Gradient norm: 0.00000060 a.u.
Point group: Dinfinityh
Bond distance: 1.10550
Bond angle: 180
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES Predicted change in Energy=-3.401007D-13
test molecule |
 There are no negative frequencies
There are no negative frequencies
Optimization file: here
H2 Molecule
This molecule is hydrogen.
Calculation method: RB3LYP
Basis set: 6-31G(D,P)
Total energy: -1.17853936 a.u.
RMS Gradient norm: 0.00000017 a.u.
Bond distance: 0.74279
Bond angle: 180
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES Predicted change in Energy=-1.164080D-13
test molecule |
There are no negative frequencies
Optimization file: here
Energy of reaction
E(NH3)= -56.55776873 a.u.
E(N2)= -109.52412868 a.u.
E(H2)= -1.17853936 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579074 a.u.
E(NH3)= -148492.4218 kJ/mol
E(N2)= -287555.5998 kJ/mol
E(H2)= -3094.25509 kJ/mol
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -146.478531 kJ/mol
F2 Molecule
This is a molecule of F2.
Calculation method: RB3LYP
Basis set: 6-31G(D,P)
Total energy: -199.49825218
RMS gradient: 0.00007365
Point group: Dinfinityh
Bond length: 1.40281 angstrom
Bond angle: 180
Item Value Threshold Converged? Maximum Force 0.000128 0.000450 YES RMS Force 0.000128 0.000300 YES Maximum Displacement 0.000156 0.001800 YES RMS Displacement 0.000221 0.001200 YES Predicted change in Energy=-1.995025D-08
This is a homodiatomic molecule, with no overall charge and no polarization because both atoms are the same.
test molecule |
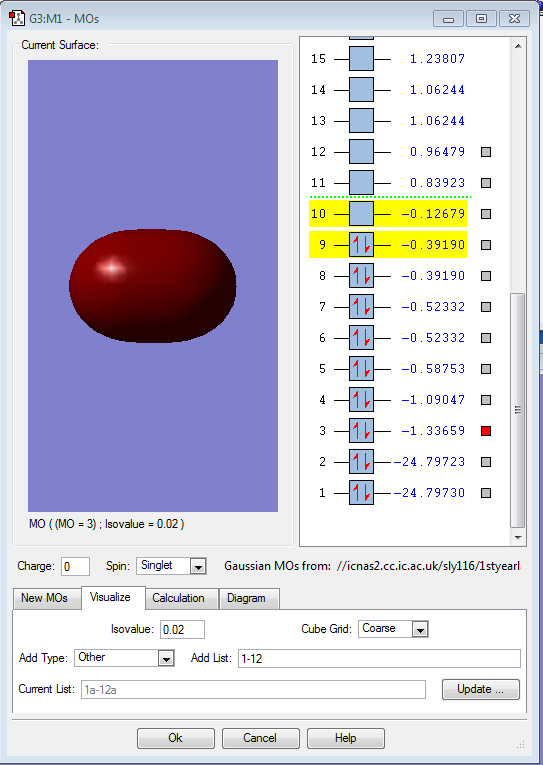
This filled MO shows the sigma bonding orbital, made up of two 2s atomic orbitals.
This, however, shows the respective sigma antibonding orbital (also filled), comprised of two 2s atomic orbitals of fluroine.
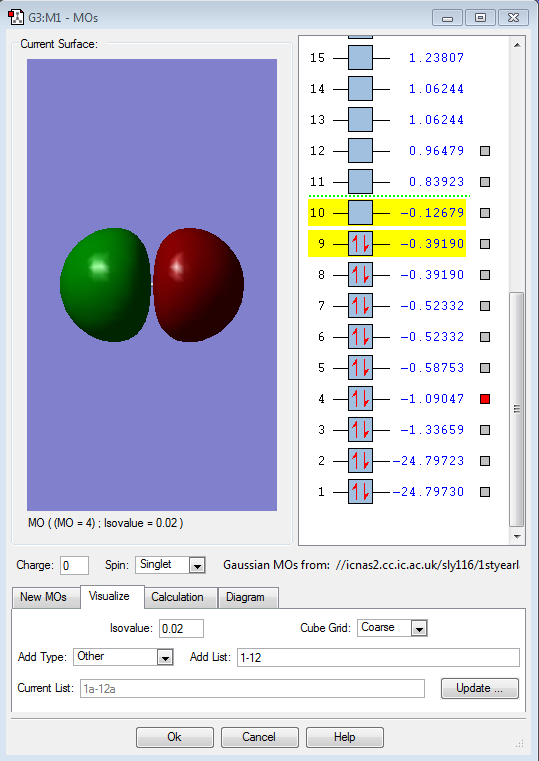
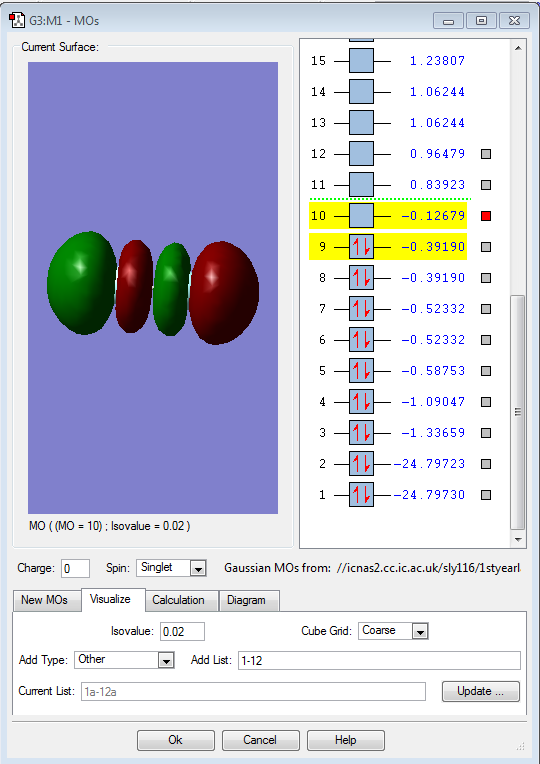
This image shows the HOMO orbital in F2, which is an antibonding pi orbital as a result of the 2p atomic orbitals.
This shows the LUMO orbtial of F2, a 2p sigma antibonding orbital.
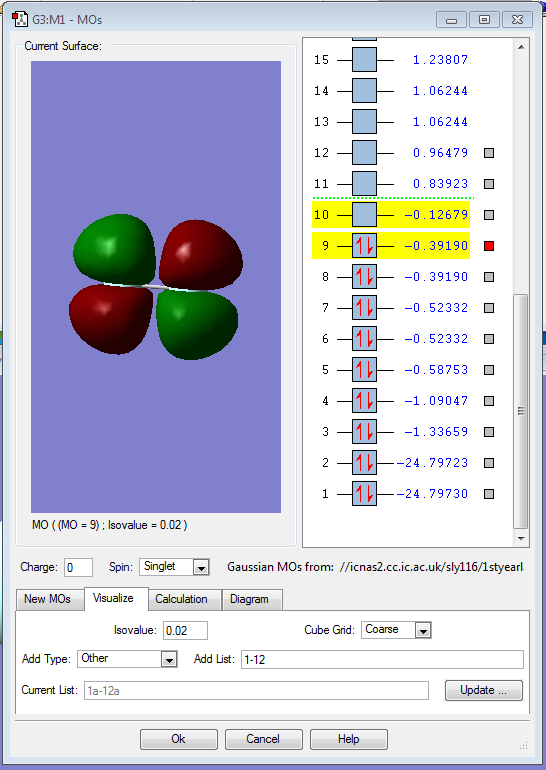
Finally, this is the shape of the 2pz bonding orbital of F2, due to the interaction of two 2p orbitals from each fluorine atom.
Optimization file: here