MolModII:1324
Set Molecules
Ammonia (NH3)
Summary
Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy E(RB3LYP): -56.55776873 a.u.
RMS Gradient: 0.00000485 a.u.
Point Group:C3V
Optimised N-H Bond Distance: 1.01798 Å
Optimised H-N-H Bond Angle: 105.741 °
Convergence Proof
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986294D-10
Optimization completed.
-- Stationary point found.
NH3 |
The optimisation file for NH3 is linked to here.
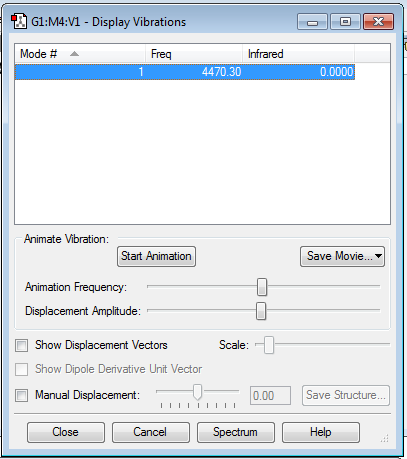
Vibrational Frequencies and Partial Charges
Questions
1) From the 3N-6 rule, we would expect (3x4-6) = 6 modes. 2) 4 of the modes are degenerate; #2 & #3, and #5 & #6. 3) Modes #1, #2 & #3 are bending modes, and modes #4, #5 & #6 are stretching modes. 4) Mode #4 is highly symmetric. 5) Mode #1 is what's known as the "umbrella" mode. 6) You would expect to see 2 bands in the experimental spectrum of gaseous ammonia, one for mode #1, and one for modes #2/#3. Modes #4, #5 & #6 are not intense enough to be seen.
Charge on N atom: -1.125 Charge on H atoms: +0.375
This is broadly similar to what I expected, as N is more electronegative than H, so N will pull electron density towards it from each of the H atoms, and each of the H atoms will lose some electron density, resulting in H being positive and N being negative.
Nitrogen (N2)
Summary
Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy E(RB3LYP): -109.52412868 a.u.
RMS Gradient: 0.00000365 a.u.
Point Group: D∞h
Optimised N≡N Bond Distance: 1.10550 Å
Convergence Proof
Item Value Threshold Converged?
Maximum Force 0.000006 0.000450 YES
RMS Force 0.000006 0.000300 YES
Maximum Displacement 0.000002 0.001800 YES
RMS Displacement 0.000003 0.001200 YES
Predicted change in Energy=-1.248809D-11
Optimization completed.
-- Stationary point found.
N2 |
The optimisation file for N2 is linked to here.
Vibrational Frequencies and Partial Charges
The vibrational data is as expected, with there only being one mode (a stretching mode), which works with the 3N-5 rule for linear molecules, of which this is one. The intensity of this mode is also 0, which is to be expected as N2 is a homonuclear diatomic molecule, so its stretching vibration results in no change in its dipole moment, and so is not detected by IR spectroscopy. The frequency of the vibrational mode also seems sensible, as it is relatively high, as stretching modes often are, but not as high as the stretching mode of H2 (see later), as bonds with H atoms often have higher frequency modes.
Charge on each N atom: 0.000
Hydrogen (H2)
Summary
Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy E(RB3LYP): -1.17853929 a.u.
RMS Gradient: 0.00013423 a.u.
Point Group: D∞h
Optimised H-H Bond Distance: 0.74247 Å
Convergence Proof
Item Value Threshold Converged?
Maximum Force 0.000232 0.000450 YES
RMS Force 0.000232 0.000300 YES
Maximum Displacement 0.000305 0.001800 YES
RMS Displacement 0.000431 0.001200 YES
Predicted change in Energy=-7.091616D-08
Optimization completed.
-- Stationary point found.
H2 |
The optimisation file for H2 is linked to here.
Vibrational Frequencies and Partial charges
The vibrational data is as expected, with there only being one mode (a stretching mode), which works with the 3N-5 rule for linear molecules, of which this is one. The intensity of this mode is also 0, which is to be expected as H2 is a homonuclear diatomic molecule, so its stretching vibration results in no change in its dipole moment, and so is not detected by IR spectroscopy. The frequency of the mode is also considerably high, since H is a very light atom, and in this case produces a stretching mode, which often have considerably high frequencies.
Charge on each H atom: 0.000
Haber-Bosch Process
N2 + 3H2 → 2NH3
E(NH3) = -56.55776873 a.u
2*E(NH3) = -113.11553746 a.u.
E(N2) = -109.52412868 a.u.
E(H2) = -1.17853929 a.u.
3*E(H2) = -3.53561787 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)] = -113.11553746 - [-109.52412868 + -3.53561787]
= -113.11553746 + 113.05974655
= -0.05579091 a.u.
= -0.05579091 x 2625.5
= -146.479034205 kJ/mol
Therefore ammonia is clearly more stable than the gaseous reactants, as energy decreases in its formation.
My Molecule
Methane (CH4)
Summary
Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy E(RB3LYP): -40.52401406 a.u.
RMS Gradient: 0.00000415 a.u.
Point Group: Td
Optimised C-H Bond Distance: 1.09189 Å
Optimised H-C-H Bond Angle: 109.471 °
Convergance Proof
Item Value Threshold Converged?
Maximum Force 0.000008 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000023 0.001800 YES
RMS Displacement 0.000012 0.001200 YES
Predicted change in Energy=-3.646116D-10
Optimization completed.
-- Stationary point found.
CH4 |
The optimisation file for CH4 is linked to here.
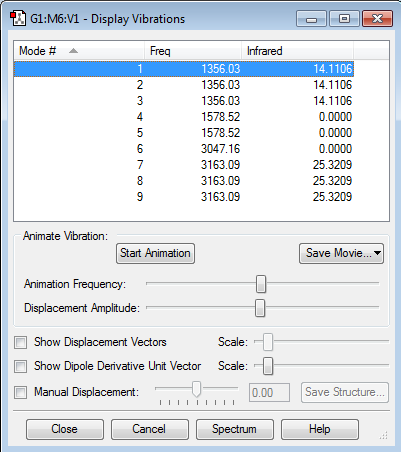
Vibrational Frequencies and Partial Charges
CH4 has 9 vibrational modes, which is to be expected according to the 3N-6 rule (3x5-6 = 15-6 = 9). 8 of these modes are degenerate; #1, #2 & #3, #4 & #5, and #7, #8 & #9. This means in total there are 2 different bands for CH4, since modes #4 , and #7 have intensities of 0, and so are not seen. The frequencies of these modes also seem sensible, as the first 5 modes correspond to bending modes, and the last 4 modes correspond to stretching, and the stretching modes have higher frequencies than the bending modes which is common. Also C is bonded to H, which often results in higher frequencies, as is the case here.
Charge on C atom: -0.930
Charge on H atoms: 0.233
These charges are as expected, as C is more electronegative than H, so pulls electron density from the H's towards it, giving C a negative charge, and each of the H's a positive charge.
Molecular Orbitals
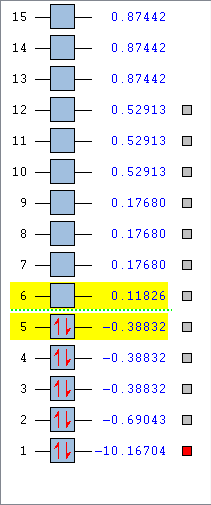
List of MOs
MO 1
This MO is in fact just the 1s AO of the carbon, and as can be seen by the list of MOs, it is so much deeper in energy than the other MOs (-10.16704 a.u. vs -0.69043 a.u. for the next lowest energy MO) than it does not contribute to bonding or mixing, and thus is what's described as a nonbonding orbital.
MO 2
This bonding MO is a combination of C's 2s orbital, and the 1s orbitals from each of the H's. All these orbitals are in the same phase, and when combined the MO contributes towards ¼ of a σ bond towards each C-H bond.
MO 3
This MO is also a bonding orbital, and is one of three MOs which are identical in energy (MOs 4 & 5). This MO is a combination of one of C's 2p orbitals, and the 1s orbitals from each of the H's. However, this time, two of H's 1s orbitals are in one phase, and the other two are in the opposite phase. The phase of the 1s orbitals corresponds to the phase of the part of C's 2p orbital which is facing it.
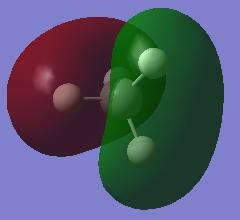
The diagram below (drawn by me) shows the positioning and phases of the 2p and 1s orbitals involved in this MO:
This MO is also HOMO in this molecule. Each of these MOs also contribute towards ¼ of a σ bond towards each C-H bond, and since there are 3 of them, and MO 2 also constitutes ¼ of a bond, these all result in the 4 C-H bonds in CH4.
MO 6
This MO is the LUMO in this molecule, and is formed from the 2s AO of carbon and the 1s AOs of the hydrogens, except this time carbon's s orbital and the hydrogens' s orbitals are out of phase, thus resulting in antibonding character. Since unoccupied, this MO does not contribute towards (or indeed, against) bonding.
MO 7
This MO is a combination of carbon's 2p orbital and the hydrogens' 1s orbitals, although in this case, the MO is an antibonding orbital, and so the difference from MO 3 is that the phase of either the p orbital or the s orbitals has switched. However, since it involves all 3 of C's 2p orbitals, there are 3 of these MOs, all equal in energy. Since this MO is unoccupied, it does not contribute to bonding.
Extra Molecule
Cyanide Ion (CN-)
Summary
Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy E(RB3LYP): -92.82453153 a.u.
RMS Gradient: 0.00000977 a.u.
Point Group: C∞v
Optimised C≡N Bond Distance: 1.18409 Å
Convergance Proof
Item Value Threshold Converged?
Maximum Force 0.000017 0.000450 YES
RMS Force 0.000017 0.000300 YES
Maximum Displacement 0.000008 0.001800 YES
RMS Displacement 0.000011 0.001200 YES
Predicted change in Energy=-1.280318D-10
Optimization completed.
-- Stationary point found.
CN- |
The optimisation file for CN- is linked to here.
Vibrational Analysis and Partial Charges
CN- is a linear molecule, so according to the 3N-5 rule, there should be 1 vibrational mode, which is the case. The mode is a stretching mode, and its frequency is neither particularly high nor low, which seems sensible.
Charge on N atom: -0.754
Charge on C atom: -0.245
These charges seem sensible as they add up to -1, which is the overall charge of the molecule, and nitrogen is more negative than carbon, as it is more electronegative.
Molecular Orbitals
List of MOs
MO 3
This MO is a bonding orbital, and is a combination of the 2s orbitals of both carbon and nitrogen. this orbital is the deepest in energy of all the occupied MOs (except for MOs 1 & 2, which are both nonbonding orbitals).
MO 4
This orbital is the antibonding orbital made up of the 2s orbitals of carbon and nitrogen, where the two AOs are out of phase with one another. Mixing also contributes towards the formation of this molecule; it is known to mix with MO 7, after which this MO becomes lower in energy, and MO 7 becomes higher in energy (see MO 7).
MO 5
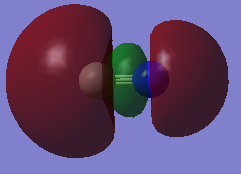
This MO, along with MO 6 with which it is degenerate, are formed from the 2p orbitals of carbon and nitrogen. They stick up perpendicular to the C≡N bond, and each MO contributes towards one π bond.
MO 7
This MO is a bonding orbital formed, again, from the 2p orbitals of carbon and nitrogen, except this time the two p orbitals are in the same plane as the bond, and thus combine to form a σ bond. This MO is also formed from the mixing with MO 4. MO 4 then becomes lower in energy, and MO 7 becomes higher in energy, and in fact becomes higher in energy then MOs 5 & 6, which were originally higher in energy then MO 7. As a result, this MO is the HOMO in this molecule, i.e. this is the MO involved in nucleophilic attack of the CN- ion.
MO 8
This MO represents the first unoccupied MO in this molecule (the LUMO), and is an antibonding orbital formed from the orthogonal 2p orbitals of carbon and nitrogen. It is equivalent in energy with MO 9.