Modjr4815
Introduction to Molecular Modelling 2 - James Rowley
NH3 molecule
Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy: -56.55776873 a.u.
RMS Gradient Norm: 0.00000485 a.u.
Point Group: C3v
N-H Bond Length: 1.3 A
H-N-H Bond Angle: 109.471°
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
Optimised NH3 |
File:JROWLEY NH3 OPTIMISATION POP.LOG
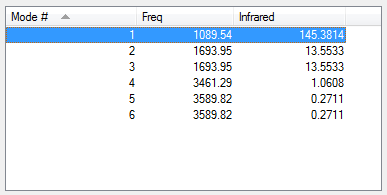
From 3N-6 rule, you would expect 6 vibrational modes in NH3. The vibrational modes 2 and 3 are degenerate (frequency of 1693.95Hz) and the vibrational modes 5 and 6 are degenerate (frequency of 3589.83Hz). Vibrational modes 1,2 and 3 are bending vibrations; modes 4,5 and 6 are stretching vibrations. Vibrational mode 4 is highly symmetric. Vibrational mode 1 is the umbrella mode. You would expect 4 bands in an experimental spectrum of gaseous ammonia.
The charge on the N-atom is -1.125 and the charge on the H-atoms are +0.375. You expect the charge on the N-atom to be negative as it is the most electronegative atom in NH3; conversely you expect the H-atoms to have a positive charge as they are more electropositive.
N2 molecule
Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy: -109.52412868 a.u.
RMS Gradient Norm: 0.0000006 a.u.
Point Group: D∞h
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
Optimised N2 |
File:JROWLEY N2 OPTIMISATION POP.LOG
There is one vibrational mode in N2 of the frequency 2457.33Hz
H2 molecule
Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy: -1.17853936 a.u.
RMS Gradient Norm: 0.00000017
Point Group: D∞h
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
Optimised H2 |
File:JROWLEY H2 OPTIMISATION POP.LOG
There is one vibrational mode in H2 of the frequency 4465.68Hz
Haber-Bosch Reaction Energies
E(NH3)= -56.55776873 a.u.
2*E(NH3)= -113.1155375 a.u.
E(N2)= -109.52412868 a.u.
E(H2)= -1.17853936 a.u.
3*(H2)= -3.53561808 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579074 a.u. = -146.48 kJ/mol
The reaction is exothermic so ammonia (gaseous product) is more energetically stable.
However, the true value of the enthalpy change of this reaction is -46.22kJ/mol[1]. The value calculated from the data from Gaussian is inaccurate due to the approximations made by the calculation method.
Silane (SiH4)
Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy: -291.88802760 a.u.
RMS Gradient Norm: 0.00000002 a.u.
Point Group: Td
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
Optimised SiH4 |
File:SIH4 OPTIMISATION POP.LOG
Vibrational modes 1,2 and 3 are degenerate and are all bending vibrations. Vibrational modes 4 and 5 are also degenerate and bending vibrations. Vibrational modes 6,7 and 8 are degenrate and are stretching vibrations. Finally, the ninth vibrational mode is a stretching vibration.
The silicon atom has a charge of +0.629 and each hydrogen atom has a charge of -0.157 so hydrogen is more electronegative than silicon.
This molecular orbital is formed from the 1S atomic orbital of the silicon atom. It is very deep in energy and is a non-bonding orbital and it is occupied.
This molecular orbital is also non-bonding and is formed from the 2S atomic orbital of the silicon atom. It is deep in energy and occupied.
There are three of these molecular orbitals all of the same energy and orthogonal to each other. These are non-bonding, occupied orbitals formed from the 2P orbitals of silicon. They are deep in energy
This molecular orbital is the first bonding orbital of SiH4 and is formed from the overlap of 3S orbital of the silicon with the 1S orbitals from the hydrogen atoms. It is occupied and deeper in energy than the HOMOs.
This is the first pi-bonding orbital of silane; there are three of these (all degenerate). They are the HOMOs of silane and are formed from the overlap of the 4 1S orbitals of the hydrogen with the 3P orbitals of the silicon atom. All three of these orbitals are occupied.
Enthalpy of formation of silane:
Si + 2H2 → SiH4
E(Si)= -289.32890164 a.u.
E(H2)= -1.17853936 a.u.
E(SiH4)= -291.88802760 a.u.
ΔE=[E(SiH4)]-[E(Si)+2*E(H2)] = -0.20204724 a.u. = -530.47 kJ/mol
However, the true value of this is -51.7kcal/mol = -216.3128kJ/mol (reverse of the enthalpy change associated with the thermal decomposition of silane)[2]. Once again the inaccuracy of the calculation is due to the approximations made by the calculation method.
References
[1]Y. Bicer, I. Dincer, C. Zamfirescu, G. Vezina, F. Raso, Journal of Cleaner Production, 2016, 135, 1379-1395
[2] T.R. Hogness, T.L. Wilson, W.C. Johnson, Journal of the American Chemical Society, 1936, 58, 108-112